整体视角下的主题式复习操作路径

应佳成

摘    要：整体视角下的主题式复习基于数学的整体性和系统性，以思想方法为统领，以能够产生实质性关联的内容为主题，打破单元限制进行一以贯之的复习.教学中教师可以沿着“双基评估、四基落实、能力提升”的基本路径展开，以发展学生运算能力、推理能力和抽象能力等关键能力为目的，开展主题式复习，指向素养发展.

关键词：整体;主题式复习;乘法公式;知识链

复习的教育价值在于建立内容之间的联系，聚零为整，完善知识体系，提升思想方法，落实核心素养.从数学内部来看，同一主题下的内容往往能够产生实质性联系：“数学内容尽管多样，但在本质上是一个整体，不同知识之间，不同主题、单元之间都存在实质性联系.”由于新课阶段是以分解的、局部的方式学习和认识新知识，难以获得对学习对象的整体全面认识，因而主题式复习直指弊端，基于数学的整体性和系统性，以思想方法为统领，以能够产生实质性关联的内容为主题，打破单元限制进行一以贯之的复习，目标指向学生的素养发展.

主题式复习如何开展实施呢？本文以“乘法公式知识链的复习”为样例，从双基评估（唤醒）、四基落实（融合）、能力提升（升华）三个层次展开具体研究.

一、测评辨析   回顾知识内容

本阶段通过解决结构相似、操作步骤一致的问题回顾乘法公式知识链，理解知识链上每一环之间的关联.

（一）分级前测   评估双基

由于主题式复习横跨初中三年的内容，因此需要“唤醒”基础知识，同时对基础知识和基本技能做出水平评估，“前测”是重要的唤醒手段.知识的获取是一个新知识与学习者已有的旧知识结构相互影响的整合过程，基于“前测中困惑的问题形成的个体经验会影响个体知觉和注意，形成对学习材料的问题解决信息加工的倾向和偏好，这使得个体不仅唤起与问题相关的行之有效的信息，而且也能主动地对新知识进行选择性注意”原理，确定分层前测，精准发现不同层面的学生在双基上存在的漏洞，并及时做出合理有效的干预，为后续调整教学策略做好准备，让不同水平的学生在自己的能力发展区内得到最大限度的发展.

（二）分析本质   建立关联

只有深刻理解公式本质，才能在不同公式间进行主动对比，当结构发生变化的时候能够调取已有知识经验，从源头上思考问题的解决方法.要让学生明确，乘法公式源于多项式乘法运算，其原理是运用分配律逐项相乘再相加，有一些具有特殊结构的多项式相乘之后能够产生同类项，因而产生了具有特殊结构的结果，通常意义上的乘法公式就是这些具有特殊结构的多项式相乘的结果.

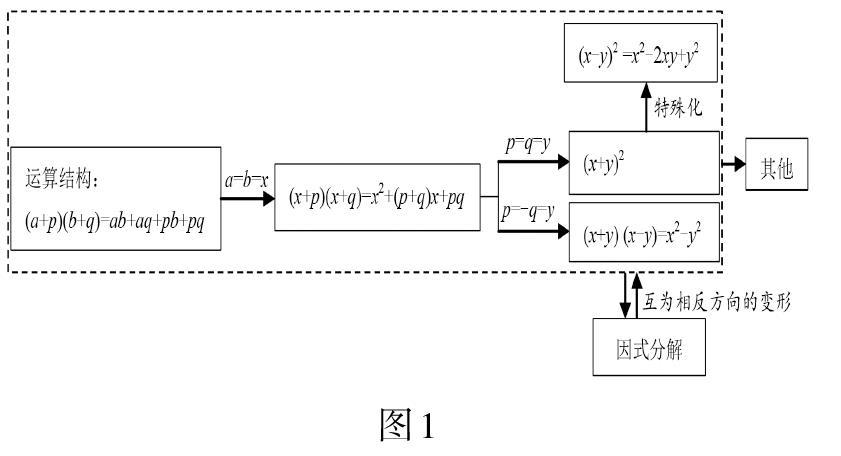
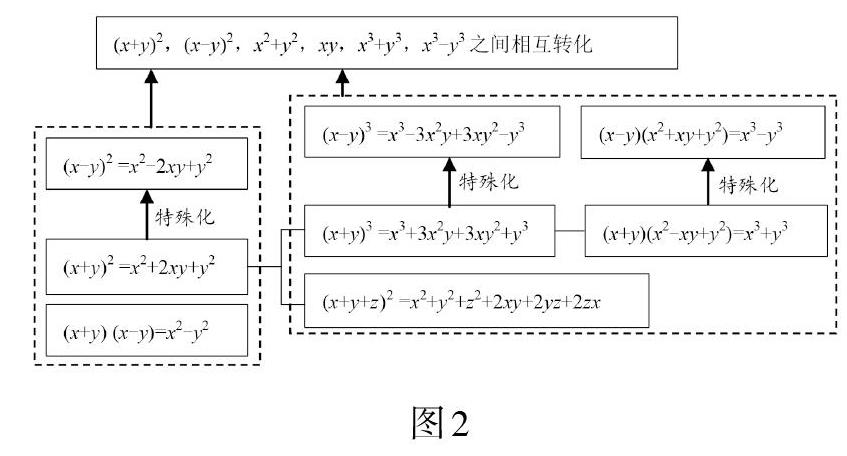
公式（x+y）（x-y）=x2-y2（平方差公式）和（x+y）2=x2+2xy+y2（完全平方公式）都是（a+p）（b+q）=ab+aq+pb+pq的特殊情形，若a=b=x，p=-q=y，则产生平方差公式（x+y）（x-y）=x2-y2;若a=b=x，p=q=y，则产生完全平方公式（x+y）2=x2+2xy+y2，详见图1.

使用了这些特殊的代数结构，可以越过程序性的展开过程直接得出结果，这种思维有助于发现概括规律，体验从一般到特殊的研究問题方式，为其他问题的研究提供类比和借鉴.对公式结构的熟练程度决定了学生能力提升的高度.事实上，公式结构不仅仅表示运算的结果，运算过程也有迹可循，并且结构特征清晰，易于依据规律识记.为了熟练使用公式，做到对公式结构了如指掌，可以设置这样的题组：

① （a+2b）2+（b+a） （b-a）;

②[（a+b）2-（a-b）2]·a;

③（a2+b2）（a2-b2）;

④（3a+2b-1）（3a-2b+1）;

⑤（[a]+[b]）（[a]-[b]）;

⑥[13-2]+[13+2].

这些问题都是直接使用公式的基本原理在运算，步骤完全一致，所蕴含的一般观念是重点，让学生明白公式的使用不局限于用a，b表示单独的数或字母，可以推广到一般意义的多项式、根式等，其意义在于将这些特定的结构作为更为一般性的结论，加深学生对知识之间关联性的理解程度，提高概括能力.

二、融合重整   构建知识系统

本阶段的落实决定了主题式复习的成败.这一阶段需要利用包容水平更高的学习材料，揭示乘法公式知识链上内容间的实质性关系，增强似是而非的知识间的可辨度，把低位经验概括归纳到高位结构中，为能力的提升提供稳定的固着点.

（一）丰富背景   识别结构

由于乘法公式是恒等式，因此可以在整式乘法和因式分解之间灵活切换问题情境，因式分解的过程是将多项式形式变形为因式相乘的形式，这是逆向思维的过程，需要理解公式、熟知公式的结构特征，对公式的多项式形式有透彻理解，对能力要求更高.因式分解在各种知识背景下都有涉及，本质就是对乘法公式结构的识别和使用.比如：

①分解因式：（a+b）2+2a+2b-3;

②分式化简：[a2-2ab+b2a2-b2];

③二次根式化简：[12-1];

④解一元二次方程：x2-2x+1=0;

⑤求关于x的二次函数y=ax2+2a （a+2）x+a2+4a+4的图象与x轴的交点坐标;

⑥已知△ABC的三边分别为a，b，c，且a=7，b=24，c=25，判断△ABC的形状;

……

这一组问题显示了乘法公式的广泛使用：涵盖分解因式、分式运算、二次根式运算、解方程、二次函数、几何计算等内容，通过这样大量的、丰富的问题情境转换，帮助学生理解公式结构，增强知识的可辨度，构建运算思路.比如题⑤，解决通法是借助函数与方程的关系，将二次函数转化为一元二次方程，利用求根公式解决问题，但是此法明显不够简洁，如果熟悉完全平方公式的结构特征，则可快速分解因式得到y=ax2+2a（a+2）x+（a+2）2=（ax+a+2）2，直接将这个二次函数从一般形式分解成为顶点式，从而发现函数图象与x轴的交点坐标为（-a-2， 0）.再如题⑥，如果直接使用72+242=252，则过程繁杂易出错，如果遇到更为复杂的数据显然不是最佳做法，但是使用平方差公式可以使问题运算大大简化，找出题目中最大的一个数为c =25，则c 2-b 2=（25+24）（25-24）=49×1=72=a2，因此△ABC是直角三角形.