布鲁氏菌病传播的微分方程模型及其动力学研究

董文文，周林华，王帅，吕堂红，葛加伟

（长春理工大学 理学院，长春 130022）

布鲁氏菌病（Brucellosis）简称布病，又称为波状热、地中海热、马耳他热。布鲁氏菌病是一种由布鲁氏菌引起的动物源性细菌人畜共患病，广泛分布全球各个国家和多种类型动物中。布鲁氏菌是最常见的实验室源性病原体，世界动物卫生组织（OIE）将其划分为B类动物传染病［1］。全球范围内的布鲁氏菌病病势处于历史最高点是在20世纪80年代中期。动物感染后的特征主要表现为生殖系统受到严重侵害。对于人类患者而言，会丧失劳动能力和生育能力。因此，研究布鲁氏菌病的传染规律、发展趋势和防控策略的重要性日益突出。用动力学模型来研究疾病的传播规律一直是数学家们常用的方法，它不仅能对传染病进行理论性分析和定量研究，还能清晰地描述疾病的流行规律［2］。同时结合观测数据，在理论上探讨不同控制措施的效果。因此，建立和分析相应的布鲁氏菌病动力学模型具有重要的理论和现实意义。

1994年Jorge和 Raul［3］利用奇异摄动理论建立了包括易感者类、流产具有传染性类、染病者类、疫苗接种者类四个类型的牛布鲁氏菌病的动力学模型，并给出了布病的爆发阈值。2014年Li Mingtao等［4］建立了包括易感者、潜伏者、感染者、疫苗接种、环境中布鲁氏菌的牛羊混合交叉传播的动力学模型。最后通过对参数的敏感性分析得出牛羊之间存在交叉传播，即使R0＜1时布鲁氏菌病也会存在，所以应该禁止混合饲养。2007年牡丹江医学院的李秋丽、夏蔚［5］根据某地区人发病率和牛羊布病发病率的数据，利用回归分析统计方法，在5种模型中进行模拟和分析，发现人布鲁氏菌病的发病率与牛羊布鲁氏菌病发病率的关系是正相关的，即牛羊布鲁氏菌病发病率增大时人类布鲁氏菌病的发病率也增大。2010年Aïnseba B等［6］建立了包含易感者、染病者的羊布鲁氏菌病动力学模型，模型中体现了直接传播与间接传播，求出基本再生数（R0=R0direcct+R0indirect），分析系统的全局稳定性，最后通过数值模拟给出不同情况下的屠宰策略对比结果。环境污染在疾病的持续存在（即当R0indirect＜1时）中发挥重要作用，但也可以控制流行病。聂静［1］研究了中国吉林省奶牛的布鲁氏菌病，依据布鲁氏菌病的传播机理，考虑环境当中病菌的传播，结合吉林省奶牛布病的现有防控措施，包括外界引入、因病淘汰、杀菌消毒等，建立吉林省奶牛布病的SEIV动力学模型。通过动力学分析，证明了各个平衡点的全局渐近稳定性。侯强等［7］建立了羊—人动力学模型，通过对内蒙古布鲁氏菌病数据参数的拟合和敏感性分析，得出在消毒和免疫这两个策略相结合的控制措施对疾病控制更加有效。

由于布病造成严重的损失，世界许多国家和地区制定了相应的防控和根除计划，在布病流行形式严重的地区疫苗免疫具有重要意义［8］。疫苗免疫是控制传染病传播的一种有效措施，在我国羊群养殖繁盛地区已经开始接种布鲁氏菌病疫苗，但接种的疫苗都是活疫苗，这种疫苗有一定的致病力，大量接触可引起感染。世界上只有少数国家主张给人接种布鲁氏菌病疫苗。早期人所接种的疫苗是灭活疫苗，现在已被免疫效果更好的冻干弱毒活菌苗代替。免疫期也由最初的6-9个月增长至1年，现在很多国家都在努力研究灭活疫苗，希望能够使布病疫苗广泛应用，从而控制布病的传播［8］。若在今后人能够广泛接种布鲁氏菌病疫苗，这将对控制布病起到不可忽略的作用。

本文主要根据内蒙古布鲁氏菌病传播疫情建立了羊—人耦合的传播动力学模型，主要研究人接种布鲁氏菌病疫苗对布病传播的影响。

1 模型建立和分析

1.1 模型建立

本文建立一个血清反应阳性羊—人类布鲁氏菌病传播的动力学模型，该模型中将羊群分为：易感羊群（SS）、感染羊群（IS）、接种疫苗的羊群（VS）和易感人群（SH）、感染人群（IH）、接种疫苗的人群（VH）。假设易感羊群接种疫苗也会有一部分羊群失去免疫成为新的易感羊群，易感羊群经过检测血清呈阳性，并且血清呈阳性的羊可以感染易感人群。布病的传播流程图如图1所示。

图1 羊—人布鲁氏菌病传播流程图

布鲁氏菌病传播动力学模型为：

其中，A1表示羊的输入量；γ1表示易感羊的疫苗接种率；1/τ1表示羊的疫苗接种有效期；β1表示易感羊到血清呈阳性羊的传染率；μ1表示羊的死亡率；ϕ表示羊的扑杀率；αSH表示感染羊到人的传染率；A2表示人的输入量；γ2表示易感人的疫苗接种率；1/τ2表示人的疫苗接种有效期；μ2表示人的死亡率。

令NH=SH+IH+VH，NS=SS+IS+VS，则系统（1）的正不变集为：

1.2 基本再生数和地方病平衡点

其中：

由文献［11］可知，系统（1）的基本再生数为：

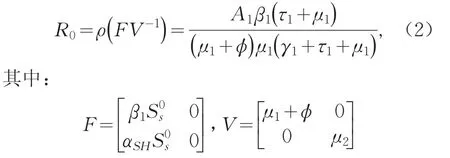
进一步，当R0＞1时系统（1）有唯一地方病平衡点。

其中：

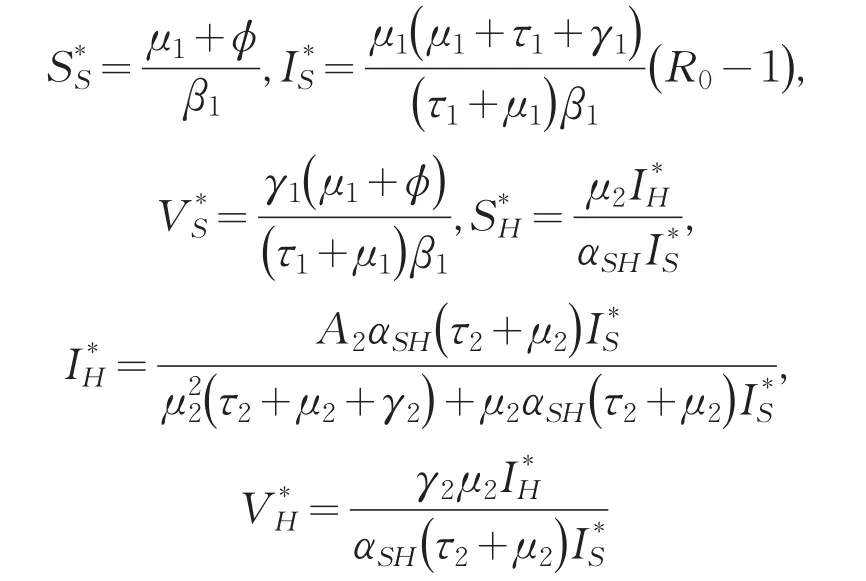
根据文献［11］中定理，有：

定理1 当R0≤1时，系统（1）的无病平衡点E0局部渐近稳定；R0＞1时，E0不稳定。

1.3 平衡点的稳定性分析

本文在这一节将完成系统（1）的无病平衡点和地方病平衡点的稳定性证明。

首先考虑系统（1）的子系统

引理1：当R0≤1时，系统（3）的无病平衡点全局渐近稳定。

证明：对系统（3）构造一个Lyapunov函数：

函数L1沿系统（3）的全导数为：

当R0≤1时，表达式。当且仅当时，等式。所以由LaSalle不变集原理可知，当R0≤1时，系统（3）的无病平衡点是全局渐近稳定的。

定理2 当R0≤1时，系统（1）的无病平衡点E0全局渐近稳定。

证明：系统（1）的前三个方程独立于后三个方程，由引理1可知系统（1）的前三个方程的无病平衡点全局稳定。接下来考虑除（3）以外的方程:

当R0≤1时，。系统（4）的极限系统为：

综上，系统（3）和（4）的无病平衡点都是全局渐近稳定的，所以系统（1）的无病平衡点E0全局渐近稳定。

下面证明地方病平衡点E*的渐近稳定性。

引理2：当R0＞1时，系统（3）的地方病平衡点全局渐近稳定。

证明：对系统（3）构造Lyapunov函数：

函数L2沿系统（3）的全导数为：

定理3当R0＞1时，系统（1）存在唯一正平衡点E*，且在集合X内全局渐近稳定。

证明：当R0＞1时，系统（4）的极限系统为：

综上，系统（3）和（4）的地方病平衡点都是全局渐近稳定的，所以系统（1）的地方病平衡点E*全局渐近稳定。

2 控制策略的数值仿真

本节主要观察羊的疫苗接种与人的疫苗接种情况对感染人数量的影响.选取系统（1）的初值如下，参数的取值如表1所示。

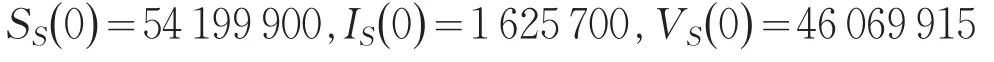
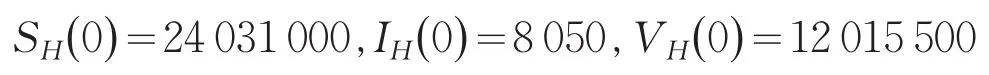
表1 参数以及参数值

图2 γ1和γ2对IH的影响

在图2中，假设羊的扑杀率ϕ=0.3为定值，通过改变γ1和γ2的值观察IH的变化。从图中可以看到随着γ1值的增大IH的曲线呈下降趋势。这说明加大羊群的疫苗接种率可以减少人类感染布鲁氏菌病的数量。比较图2中的三个图不难发现增加γ2的值，IH的值明显减小，这说明加大人的疫苗接种率可以更好的减少人感染布鲁氏菌病的数量。通过图像的对比，可以知道同时增加羊和人的布病疫苗接种率，这样能够更好的减少人的患病数量。

接下来分析基本再生数中的参数对基本再生数的影响，基本再生数的表达式如下：

通过表达式可以发现较为重要的参数为易感羊的疫苗接种率γ1和羊的因病扑杀率ϕ。考虑到参数的敏感性，首先固定其它参数不变，只看这两个变量对基本再生数的影响。从图3中不难发现当γ1大于A点的值，ϕ大于B点的值时，R0＜1说明此时疾病可以控制。同时增大γ1和ϕ的值，R0的值越小，说明同时采取两个措施，布病的防控效果越好。

图3 γ1和ϕ对基本再生数R0的影响

3 结论

在内蒙古地区，布鲁氏菌病是威胁人畜公共健康的最严重的疾病之一。本文主要是以内蒙古地区作为研究区域，建立羊—人耦合的布鲁氏菌病传播动力学模型，模型中考虑人接种布病疫苗这一项。由1.3的结论可知当R0≤1时，系统（1）的无病平衡点E0全局渐近稳定；当R0＞1时，系统（1）存在唯一正平衡点E*，且在集合X内全局渐近稳定。根据图2的对比结果，知道人的布病疫苗接种率越大，人的感染数量越少，这意味着人接种布病疫苗能够有效控制布鲁氏菌病的传播。且同时增大羊和人的疫苗接种率，人的感染数量越小，这说明同时对羊和人进行疫苗接种，可以更好的防控布病的传播。通过对基本再生数中参数的敏感性分析可知，羊的扑杀率ϕ对R0的影响大于羊的疫苗接种率γ1对R0的影响，这说明一旦发现感染羊应对其进行扑杀，这样才能更好的控制布病的传播。若同时采取两种措施且增大ϕ和γ1的值，R0的值会越小，说明布病的防控效果会更好。所以应该从疫苗接种和感染羊的扑杀两方面出发实施防控措施，控制布鲁氏菌病的传播。