具有食饵避难响应的优化的Leslie-Gower捕食模型的稳定性研究
2020-01-07李建丽张秀锋
焦 媛,李建丽,张秀锋
(长治学院 数学系,山西 长治 046011)
0 引言
由于生物环境中捕食者和他们的猎物之间的动态关系具有普遍存在性和重要性.长期以来这个问题一直是生态学和数学生态学的重要主题,Leslie[1]介绍了以下两个物种的Leslie-Gower 捕食模型:
(1)
此时的X(t),Y(t)代表的是关于时间t的被捕食者和捕食者物种数量,参数r1和r2分别是被捕食者和捕食者的固有增长率,b1衡量了物种X(t)的个体竞争力.r1/b1的值含义是被捕食者在没有捕食者的情况下的环境承载能力.p(X)是反应捕食者消耗被捕食者的响应函数并且与捕食者的物种增长速率r2和环境承载能力r2X/a2与捕食者的数量是成正比的.a2代表的是被捕食者提供给食肉动物并转化为其自身价值.项Y/X是Leslie-Gower 项,用于衡量捕食者物种数量中由于缺乏最喜欢食物而造成的损失.
改良的Leslie-Gower 和 Holling-type II 捕食模型:
(2)
我们通过加上环境或人为对被捕食者的保护mx来拓展模型(2),此时有m∈[0,1)是常数.那么此时只剩下(1-m)x可以为捕食者来利用,则根据系统 (2) 有改进的系统为:
(3)
许多作者认为,随着环境中的生物和环境本身变化提出和研究非自治系统是十分合理的[2-4].
本文先通过解微分方程证明其物种数量的有界性和持续性,来以此说明系统的可操作性,对生物种群没有破坏性.再应用雅克比矩阵证明其非负平衡和线性稳定性,则我们得到物种在这种操作下会最终达到平衡;最后我们运用李雅普诺夫函数和比较定理证明此系统具有全局稳定性,来反映带有食饵避难响应的改进的捕食模型具有积极效应.
1 有界性
引理1对于系统 (3),t∈[0,A)A=+,有
(4)
以及
(5)
证明 从系统 (3) 的第一个方程,我们可以得到对于所有的t∈[0,A),
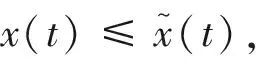
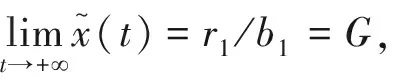
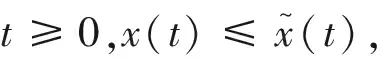
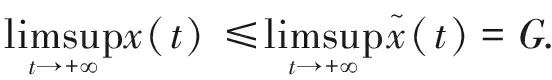
(6)
从捕食者方程中,可以得到
根据比较定理论证则有,
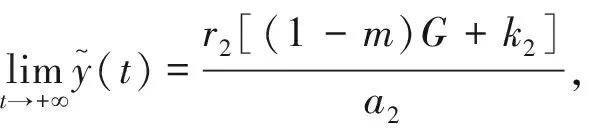
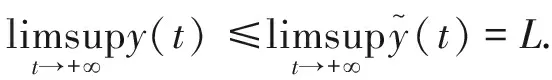
(7)
同样的也有
2 持续性
定义1若系统 (3) 中存在值α,β,且0<α<β, 此时是独立于初始条件的情况,且对于系统的所有的解x(t),y(t)有
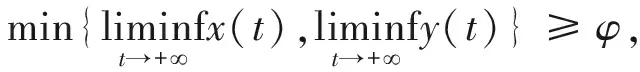
以及
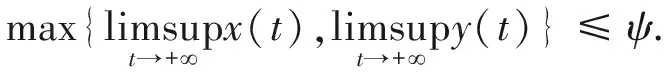
那么,系统 (3) 是持续性的.
定理1如果
(8)
则,系统 (3) 是持续性的,
证明 根据引理 1,存在一个ψ=max{G,L}>0,是独立于初始条件的,即
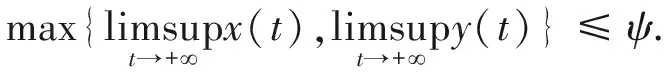
我们仅仅需要证明另有一个变量φ>0,它的初值是独立的,即为
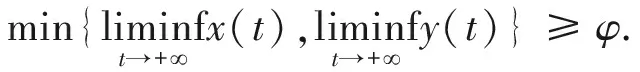
很容易看出,对于系统 (3),对于任意的μ>1以及足够大的t,有y(t)<μL.因此,得到
通过标准的比较论证,则有下面的不等式
以及令μ→1,我们获得
(9)
用式N1=1/b1(r1-a1(1-m)L/k1)来表示.如果式 (8) 的条件满足,N1>0,则通过式 (9) 和引理 1以及对任意的μ>1,存在一个正常数Tμ,对于任意的t>Tμ,有x(t)>N1/μ和y(t)<μL.那么当t>Tμ+t1时,我们有
一方面,对于t>Tμ+t1,这些不等式有
(10)
这涉及到,对于t>Tμ+t1,
(11)
另一方面,对于式 (10) 和 (11),我们有t>Tμ+t1,
因此有
令μ→1,有
接着令φ=min{N1,y1}>0.证明了系统 (3) 是持续的.
3 非负平衡和线性稳定性
式 (3) 的雅克比行列式是
(12)
如果J(E)的两个特征值的实部都是负的,则系统 (3) 的平衡值E是稳定的.因此有稳定的充分条件是
tr(J(E))<0,det(J(E))>0.
(13)
通过构造一个合适的李雅普诺夫函数来证明系统 (3) 的全局稳定性.首先,很容易验证这个系统有三个平衡点
它们的雅克比矩阵分别是
(14)
作为(13)的直接结果,有以下结果.
命题1 1)E0和E1都是不稳定的;
2)如果有a1r2k2>r1a2k1,E2是稳定的; 如果a1r2k2≤r1a2k1时E2为不稳定的[4].
命题2 系统(3)除了三个边界平衡点外,还可能有正的平衡点.假设E*=(x*,y*)是另外的平衡点,那么有
(15)
我们可以很容易地看到x*满足
a2b1(1-m)x*2+Bx*+[r2a1k2(1-m)-k1r1a2]=0,
(16)
这里B=b1a2k1+r2a1(1-m)2-r1a2(1-m),且有
Δ=B2-4a2b1(1-m)[r2a1k2(1-m)-k1r1a2],
方程 (16) 可以有两个正解,我们有以下三种情况.
情况1假设以下条件之一成立,
1)r2a1k2(1-m) 2)r2a1k2(1-m)=k1r1a2和B<0, 3)r2a1k2(1-m)>k1r1a2,B<0和Δ=0, 情况2如果有a1r2k2(1-m)>a2r1k1,B<0和Δ>0.则有式(16)有两个正解E3,±=(x3,±,y3,±) 这里的 情况3如果情况1或情况2中没有条件成立,则式 (3) 没有正的均值. 引理2假设以下条件: (17) 系统 (3) 有一个唯一的内部平衡点E*(x*,y*). 证明 从系统 (3) 中得,由于式 (15) 和 (16) 我们可以很容易地看到 (18) (19) 定理2如果有以下条件成立 (20) 2k2>k1 (21) 4[(1-m)r1+b1k1]<(1-m)2a1, (22) 则,内部平衡点E*(x*,y*)是全局渐近稳定[3]的. 证明 基于正定的李雅普诺夫函数,令V(x,y)=V1(x,y)+V2(x,y),这里得 V1(x,y)=((1-m)x*+k1)(x-x*-x*ln(x/x*)) 以及 V1(x,y)代表是系统 (3) 的解,它关于时间t的导数为 相似地,有 将方程 (15) 代入得 最后, (23) 上面的等式可以写为 这里的 由于方程 (15) 可以得到 所有的解都满足 0≤x≤r1/b10≤x+y≤L1则有, (24) 由于式 (20) 成立,则g(x,y)<0. (ii)的证明 由 为了使 Φ(x,y)<0 然后 (25) 定理3假设 a1(1-m)2r1r2+a1(1-m)b1r2k2 (H1) 2a2b1(1-m)g+[a2b1k1-a2r1(1-m)-a1r2(1-m)]>0 (H2) 而g按式(5)的定义,则系统 (3) 具有唯一的正平衡点,它是全局渐近稳定的[5]. 证明 由定理2证明中的条件 (i) 成立,因此,式 (3) 具有唯一的正平衡点.设(x(t),y(t))为 (3) 的任意正解,则有 证明否则就有根据波动引理,就存在当n→时有序列 ξn→,ηn→,τn→和σn→,也有 当n→时,有,以及因此, 相似地,也有 (26) 接下来,从等式 (3) 的第一个方程有, (27) 接着两边取极限n→,则可以得到再结合式 (26),有如下所示, 相似地,可以证明 即有 定理4设系统 (3) 具有唯一的正平衡点E*=(x*,y*),并进一步设 (H3) 这里的L在式 (4) 中定义,则E*是全局渐近稳定的. 证明 令(x(t),y(t))是系统 (3) 的正解,从条件 (H3)中,设ε>0,这样的话就有 (28) 也就是说,从式 (4) 中可以得到存在T>0的以下结论成立, 0 (29) 根据定理2的证明,得 那么,通过x取值的正值性,以及式(28)和(29)有 因此,E*(x*,y*)是全局渐近稳定的. 本文通过对具有食饵避难响应的改进的捕食系统的物种数量的有界性、持续性、非负平衡和线性稳定性以及全局稳定性进行了研究和证明.表明对猎物适当的人为保护或自然选择,既不会破坏生态平衡,又可以对稀有物种进行适当的人为保护,具有很重要的研究价值.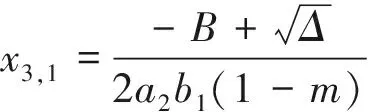
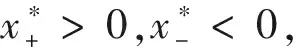
4 全局渐近稳定性
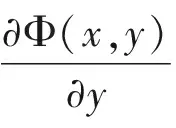
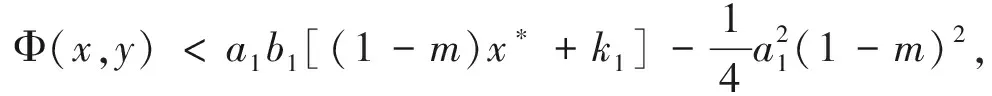
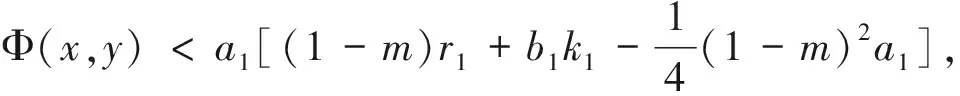
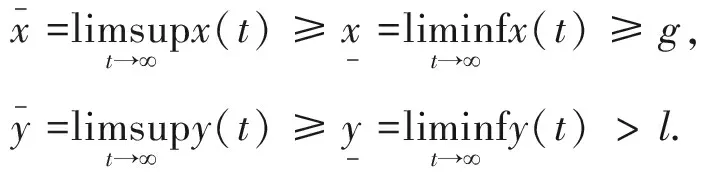
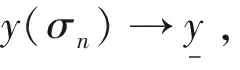
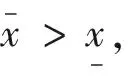
5 本章小结
