从“画饼请客”说起

郭炳校

摘 要：让学”是“引思”的前提与保障。教师只有围绕真实有效的数学规律，真诚地给学生以探究的机会，抱着真情的期待，并给以探究过程的真切体验，这样才能实现有效的“引思”，提升学生的数学学习核心素养。

关键词：小学数学；让学；生本化；启发式教学；思维课堂

古代有个人，去拜见当地有名的“吝啬大师”。老师不在家，师母叫仆人递上一只空杯，说：“请用茶。”又用两手合了一个圆圈模样，说：“请吃饼。”老师回来直躲脚，说：“你太破费了！”又用手合了半个小圆圈，说：“半个饼就足够了！”

读罢笑话，不由联想到“虚情假意”这个成语，想想时下老师讨论非常热烈的“让学引思”这个主题，其实颇为类似。“让学”强调的是教师要留足可以供学生思考、探讨数学问题的空间与时间。“引思”是在对学生数学思考、探究过程的引领、指导与帮助。笑话中，请是前提，吃是结果，当递上假食物饼时，吃就成为痴心妄想，请就成为骗人的鬼话；“让学”过程中，“让”是前提，“学”是结果。当“让”显现虚情时，“学”就成为空中楼阁，“引”就无从谈起。以下笔者结合教学体会，与同行探讨如何有效“让学”的问题。

一、真实：“让”得精准，“引”及本真

数学规律往往通过法则、公式显现，如果教师用教条化的法则、冷冰冰的公式甚至是教师自己总结的解题方法去替代有意义的算理教學与知识梳理，一不小心那就会偏离方向，出现“假饼送人”的状况，学生当然不会接受。以下是两种教法下的小数加减法计算法则的探究过程：

教法1：教师引导学生回顾整数加减法的计算法则，总结得出整数加减计算方法是末位对齐，然后让学生探究小数加减法的计算法则，得出小数加减法必须小数点对齐，然后强调二者的不同，请学生牢记。

教法2：教师引导学生回顾整数加减法的计算法则，首先问：为何35+103中第二个加数中的3要对齐上边的5，而不是3呢？假如这里拿3与3对齐，会犯什么错误呢？此时教师让学生举一个生活中不同单位的数量不能加的例子，有学生举出了“3千克桃子加3本书，等于6，然后后边的单位既不能是本，也不能是千克，所以不能加。”这样就引导学生再次明确“相同数位对齐”这一原理。然后出现小数加法：35.2+103.42，105.6+56，再次强化“相同数位对齐”并演变为“小数点对齐”，再问学生：小数点对齐是否一定正确，为什么？（当然不行，还要把相同数位对齐才行）

显然，教法1中“末位对齐”，如迁移到小数加减中就会产生错误。这里的逻辑关系中，“相同数位对齐”是本，“末位对齐”与“小数点对齐”充其量只是“末”，都有“假酒”之嫌，本末倒置就会出错。只有重视“相同数位对齐”把小数加减运算的方法跟整数加减法整合统一起来，才能把数学思维由错综复杂引向简单明了。

二、真诚：“让”之有疑，“引”之原味

“兴趣是最好的老师”，此话不假，但许多故事情境对于数学学习只是一种外部兴趣，远看很诱人，近看呢——充其量是一个“假饼”！比如“3的倍数的特征”的教学，教材给出了一百以内的自然数让学生探究。有的教师就外加设计一些童话故事类的情境，只能说是虚化课堂探究的实质，转移学生对数学规律的注意，甚至造成学生主动听故事、被动接受知识的坏习惯。

笔者在教学中，替学生设计了这么一个探究的引子：①请找出下列数中能被2整除的数并说说相关特征：12；35；38；64；85；95；96；②请找出下列数中能被5整除的数并说说相关特征：15；30；38；60；84；95；96；③请找出下列数中能被3整除的数并说说相关特征：6；9；33；66；93；95；96；102；103。学生普遍感觉很轻松，很快把符合条件的数划了出来，前两组正确率几乎百分之百，第3组的最后，有80%以上的学生选择了103，舍弃了102，并给出了理由：因为个位3能被3整除，而个位2不能。老师却在103后边打了一个大大的叉，给102打了一个大大的勾！大部分学生一片哗然，都问：“老师，难道找被3整除的数不是只看个位吗？老师说：“我有说过，只看个位吗？”学生学生陷入沉思之中。

课堂探究最忌一帆风顺，由于教师故意设局，使得学生得出了错误的结论，而这个结论一里旦被打倒，就会激起学生极大的疑惑，陷入一种“愤悱”的状态，并由此形成极大的探究热情。“让学引思”框架之下，我们把“让学”落实于真真切切的数学知识本身，才把“引思”落脚在实实在在的探究过程之上。

三、真情：“让”有风度，“引”出广度

建构主义教学理论认为，学生在学习新知识时总是倾向于从已有经验中寻找生长点，拓展出新的认知结构，教师在“让学”的过程中需要有足够的“风度”——相信学生，真情期待，在“引思”的过程中才能体现足够的“广度”。

紧接着，教师又问：大家有没有发现，梯形与三角形面积公式都能通过平行四边形的面积改变得到，都有一个“÷2”，那么我们是不是可以发现梯形与三角形面积之间的特殊关系呢？在教师的追问下，学生终于又得出：（1）当梯形上底渐近0的时候，公式中的b就消失成为三角形的面积公式了。（2）画出梯形的一条对角线，梯形面积就等于分割出的两个三角形面积之和。这样学生又建立了三角形与梯形之间的联系，还因此而渗透了极限思想与数形结合思想，增强了知识的灵动性与思维的创造性。

四、真切：“让”出主见，“引”之灼见

课堂教学是一个不断纠正学生头脑中错误认识，更新错误方法的的过程。课堂教学既要让学生有主见，更要理性对待“主见”，引导学生把主见培养成“灼见”。让学生经历真切的探究过程，在峰回路转中，形成真切的感受，有助于培养良好的思维品质与学习态度。

如下边的一道数学探究题：瓜渚湖公园有多条道路（图4），小明沿中间直线来回走一次，而小强选择沿中间的三个小圈作8字形回绕，小东则选择沿外边的大圈跑，请问他们都从A点发回到A点处，试比较走的路程谁最长，谁最短。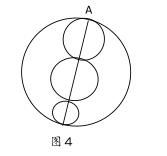

在这道探究题中，有不少学坚持认为小东走的路程比小强当要长，我问他们理由又答不上，其实在他们的头脑中冥冥地认为应该是越靠外围的圆越长，这就是“相当然、应该”之类主见的缺陷了。我没有马上否定他们的想法，只是引导他们用学过的数学知识解决问题，不要犯“想当然”的毛病。经过思考与分析，终于有学生通过用字线表示相关线段得出小强与小东的路程是相同的结论，以严密的数学思考给那些信口开河的学生来了“当头一击”。这说明，教师一开始让学生说，哪怕说得不对也不作简单否定，只是引导他们想问题要利用数学知识，这样就使“让学”给“主见”的发表提供了机会，有助于把“主见”上升到“灼见”。

总之，“让学”是“引思”的前提与保障。“桃李不言，下自成蹊。”教师只有围绕真实有效的数学规律，真诚地给学生以探究的机会，抱着真情的期待，并给以真切的数学探究过程，才能实现有效的“引思”，提升学生的数学学习核心素养。

参考文献

[1]“提问”——让课堂更精彩[J].孙乃群. 小学教学参考.2012（05）

[2]李芳.让学促思开拓教学新视角[J].基础教育研究，2016，（23）