感应同步器前处理模拟电路误差对系统测量精度影响分析

李太平 齐晓军 夏振涛

(1．上海卫星装备研究所，上海 200240；2．上海裕达实业有限公司,上海 200240)

1 引 言

感应同步器[1,2]是一种基于电磁感应原理，用于测量相对角度或者相对位移的测量元件。由于其制备材料相对较为成熟、可靠，本身具有很强的抗干扰、防辐射能力，同时具有少量污染不敏感的特点，因此得到了广泛的应用。

感应同步器研究国外起步较早，典型的如美国AER-1004、MPACS 30H系列转台等[3]；国内哈工大也做了很多研究，DPCT-2单轴伺服转台实现了高精度测量，测量精度为0.0001°[4]。早期的感应同步器测量系统多数通过反三角函数查表的方式[5～9]，直接开环测量获得感应同步器的电气转角。此种外围电路复杂，需要存储大量的反三角函数，但是其方法理论简单，所以早期的感应同步器处理芯片也采用此种算法。但是此种算法只能输出一个电气周期内的电气转角，无法获得当前系统的电气周期数，所以现在新型的解算器均不采用此种方法，而是采用II型跟踪系统自动跟踪的方法。本文据此仿真分析了感应同步器前处理电路中误差对系统测量精度的影响，并最终给出了电路误差对系统测量精度影响的理论计算公式。

2 理论分析

2.1 前置放大电路

如图1所示，SIN_C、COS_C为感应同步器的输出信号，其幅值很低，需要通过一个带通滤波器进行滤波放大，生成新的信号SIN_F、COS_F，一般幅值放大倍数不小于60dB，需要通过多级串联实现放大；R_C为原始感应同步器励磁参考信号，由于最终输入到解算电路中的参考信号需要和SIN_F、COS_F满足一定的相位关系，所以也经过一个特定的带通滤波器，生成R_F。

图1 感应同步器前处理电路输入输出信号Fig.1 Inductor synchronizer pre-processing circuit input and output signals

经过带通滤波器后的三个信号的理想数学表示分别为

SSIN_F=ASIN_FsinθsinΩt

(1)

SCOS_F=ACOS_FcosθsinΩt

(2)

SR_F=AR_FsinΩt

(3)

式中：SSIN_F、SCOS_F、SR_F——分别为图1中SIN_F、COS_F和R_F信号；ASIN_F、ACOS_F、AR_F——分别为三个信号的幅值，且满足ASIN_F=ACOS_F；θ——电气转角；Ω——励磁频率；t——时间。

2.2 跟踪算法

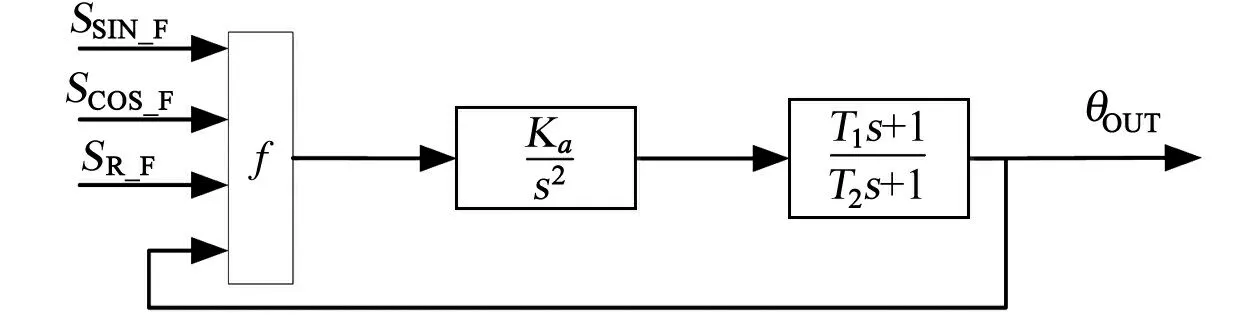
图2 跟踪算法Fig.2 Tracking algorithm

图2为系统的跟踪框图，图中：Ka=62000；T1=0.0061；T2=0.001。其中f的表达式为[10]

f=(SSIN_FcosθOUT-SCOS_FsinθOUT)SR_F

(4)

式中：f——误差生成函数；θOUT——跟踪系统的角度输出。

2.3 跟踪系统稳定性

将公式(1)、公式(2)、公式(3)代入公式(4)中，可得

(5)

式中：Δθ=θ-θOUT。

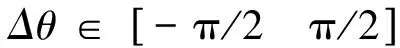
图3 线性化系统Fig.3 Linearization system

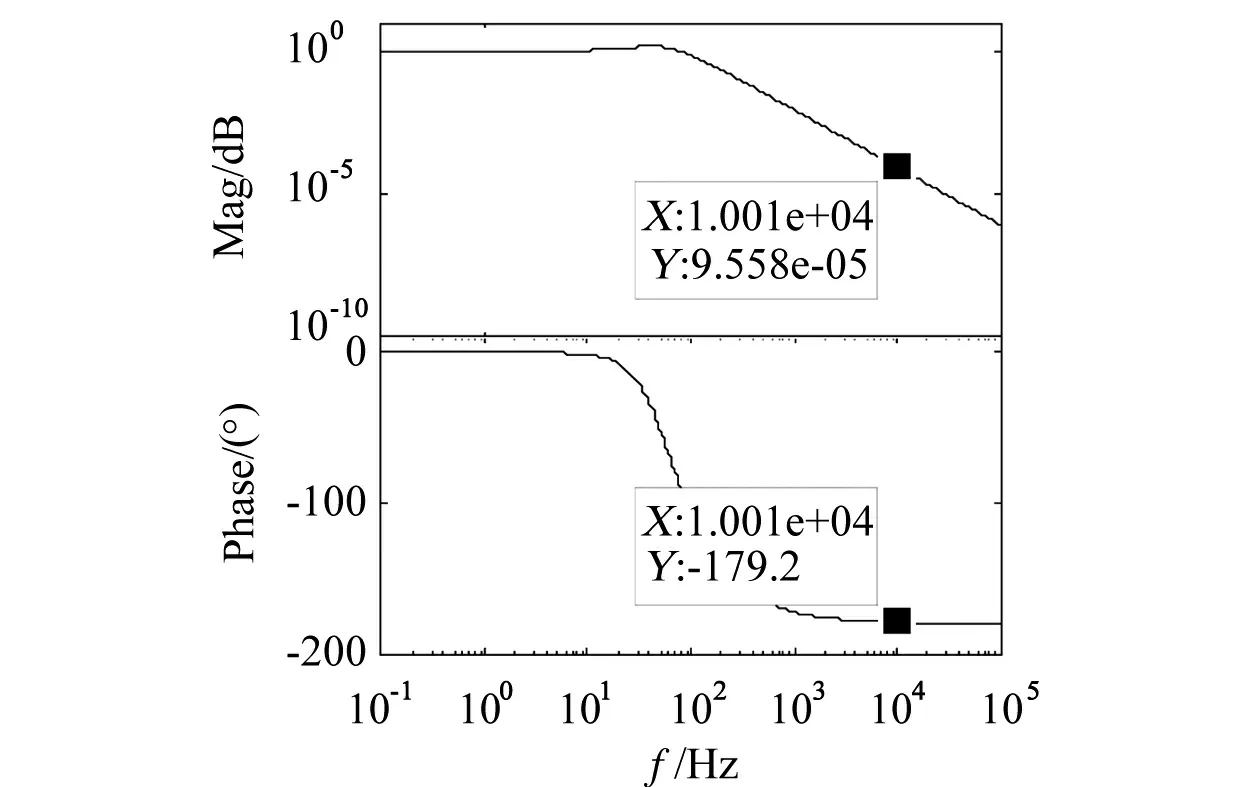
图4 系统bode图Fig.4 System bode diagram

图3所示系统的开环传递函数为

(6)

其闭环传递函数为

(7)

对于位置、速度和加速度输入信号的稳态误差为

(8)

式中：u(s)——输入信号。

由于测角系统主要用于测量角位移、角速度以及角加速度，但是在角加速度不为0时，系统处于加速状态，一般对系统的测量精度要求都不高，而对于稳态角速度和角位移，测量精度要求较高，所以以下主要是针对速度跟踪的误差进行分析。

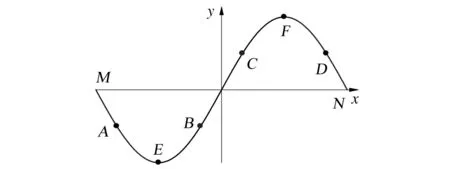
图5 系统初始误差Fig.5 System initial error

(9)

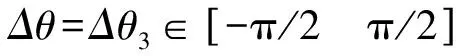
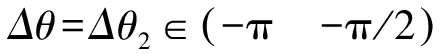
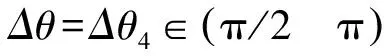
在Δθ初始分别取值-π、-3π/4、-π/4、3π/4、π时进行仿真。仿真结果如图6所示，其中x轴为时间，y轴为输出的角度，结果表明系统稳定，能够实现对系统的稳态跟踪。同时，当初值为-π和π时，显然系统的“启动”时间很长，在经过0.15s后才开始“上升阶段”，在0.15s之前，依靠频率为2Ω的高频噪声通过两次积分，使其偏离满足sinΔθ=0，但是Δθ≠2nπn∈N的点。

3 误差仿真分析

在无特殊说明下，后文的仿真均取以下参数：Ω=10kHz，θ=2πt，仿真步长不大于1×10-6s。

3.1 SIN_C、COS_C相移不同步分析

SIN_C和COS_C端的信号经过放大后，分别为sinθsinΩt、cosθsin(Ωt+φ)，φ为一个偏差小量，绝对值不大于0.05rad。输出为φ，则输入到积分端的误差函数为

esd=sinθcosφsin2Ωt-sinφcosθsin(Ωt+φ)sinΩt

(10)

令esd=0，同时，当跟踪上时θ≈φ，同时考虑2sin2Ωt=1-cos2Ωt，由公式(10)可得

(11)

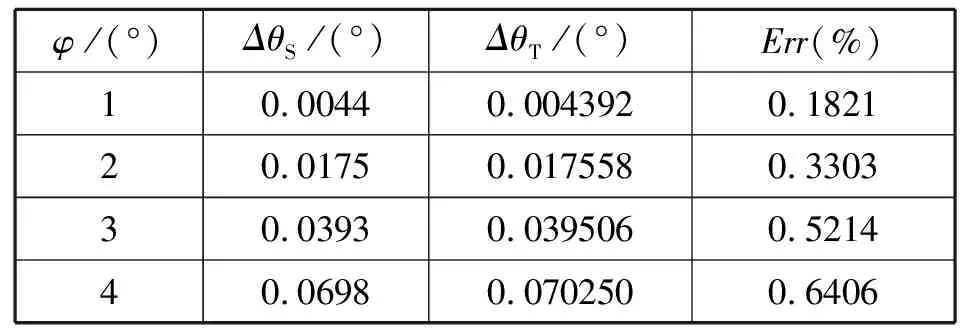
表1 不同相移下的理论误差与仿真误差

表1中：φ——SIN_C和COS_C的相位差；ΔθS——仿真得到的最大误差；ΔθT——公式(11)计算得到的最大理论误差，即公式(11)θ=π/4；Err——(ΔθS-ΔθT)/ΔθT×100%。

由图7可知，误差绝对值最大点的横坐标为θ=π/4+nπ，n为整数，与公式(11)一致。由表1可得：理论误差与仿真误差的吻合度很高，最大相对误差为0.64%，验证了公式(11)。

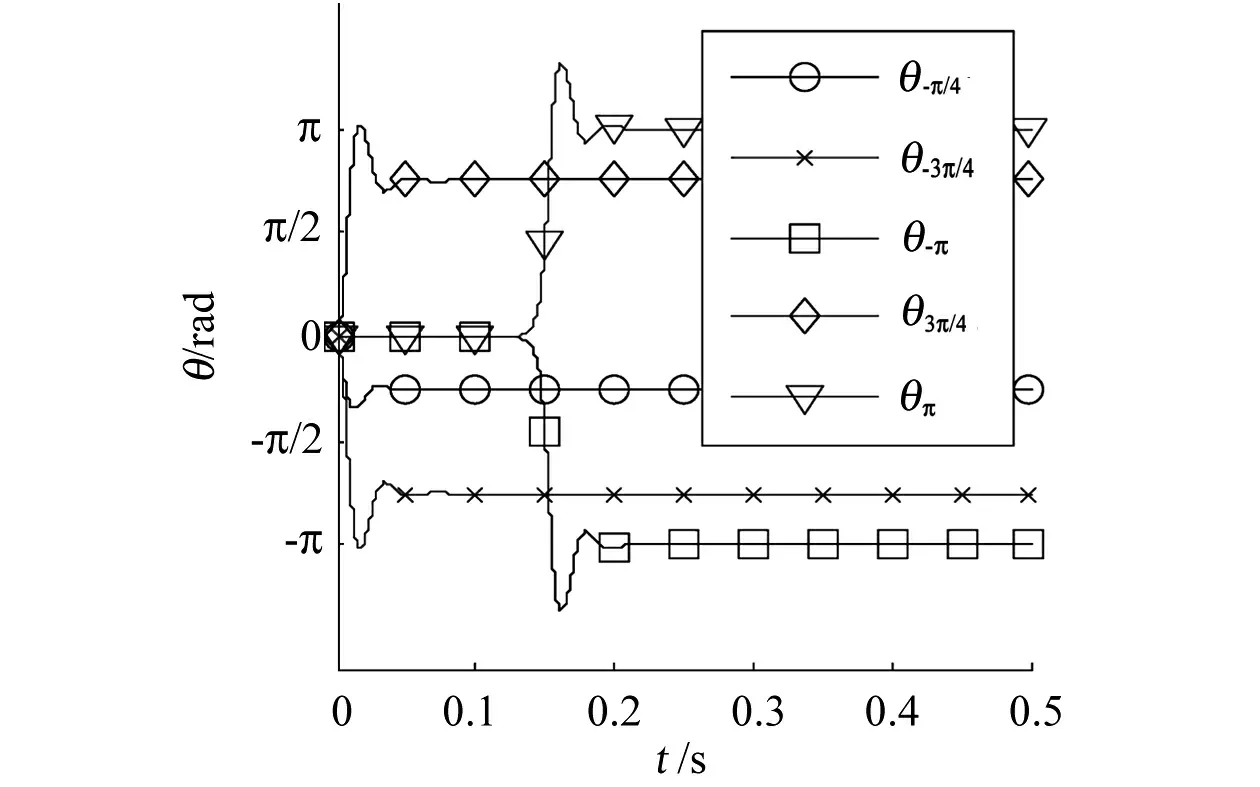
图6 系统在不同初始误差下的跟踪结果Fig.6 Tracking results of the system at different initialerrors

图7 信号不同相移下的误差结果Fig.7 Error results under different phase shifts of the signals

3.2 参考信号相位误差分析

R_C端的信号经过放大后为cosθsin(Ωt+φs)，φs为一个偏差小量，绝对值不大于0.05rad。输出为φ，则输入到积分端的误差函数为

(12)

忽略公式(12)高频项，则

(13)

所以，参考信号的相位误差相当于在图3所示的跟踪系统中的Ka乘以一个系数cosφs，cosφs为正，且保证系统仍然处于稳定状态，则不会由此产生测量误差，如图8所示。但是由于Ka发生变化，所以系统的跟踪性能发生了变化，上升时间和超调量均会发生变化，如图9所示。

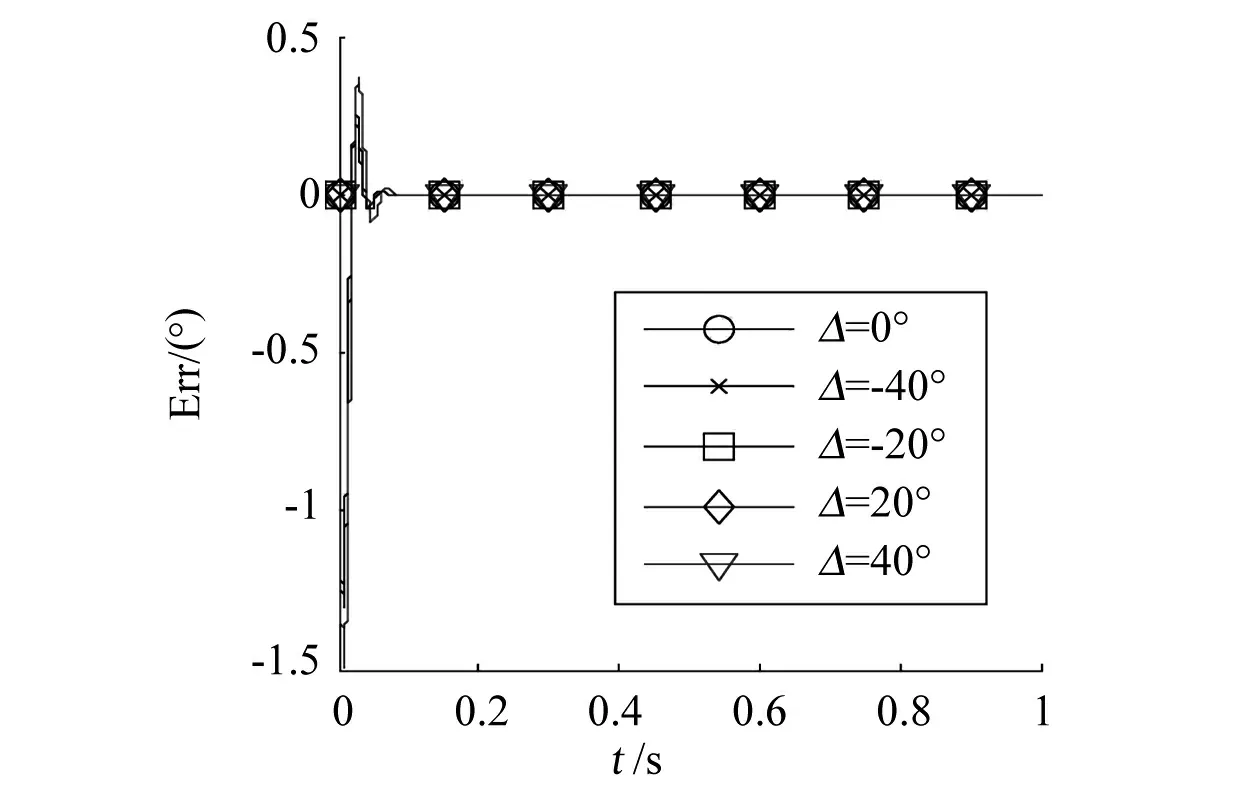
图8 参考信号不同相移误差跟踪曲线Fig.8 Tracking diagrams of reference signal different phase shift errors

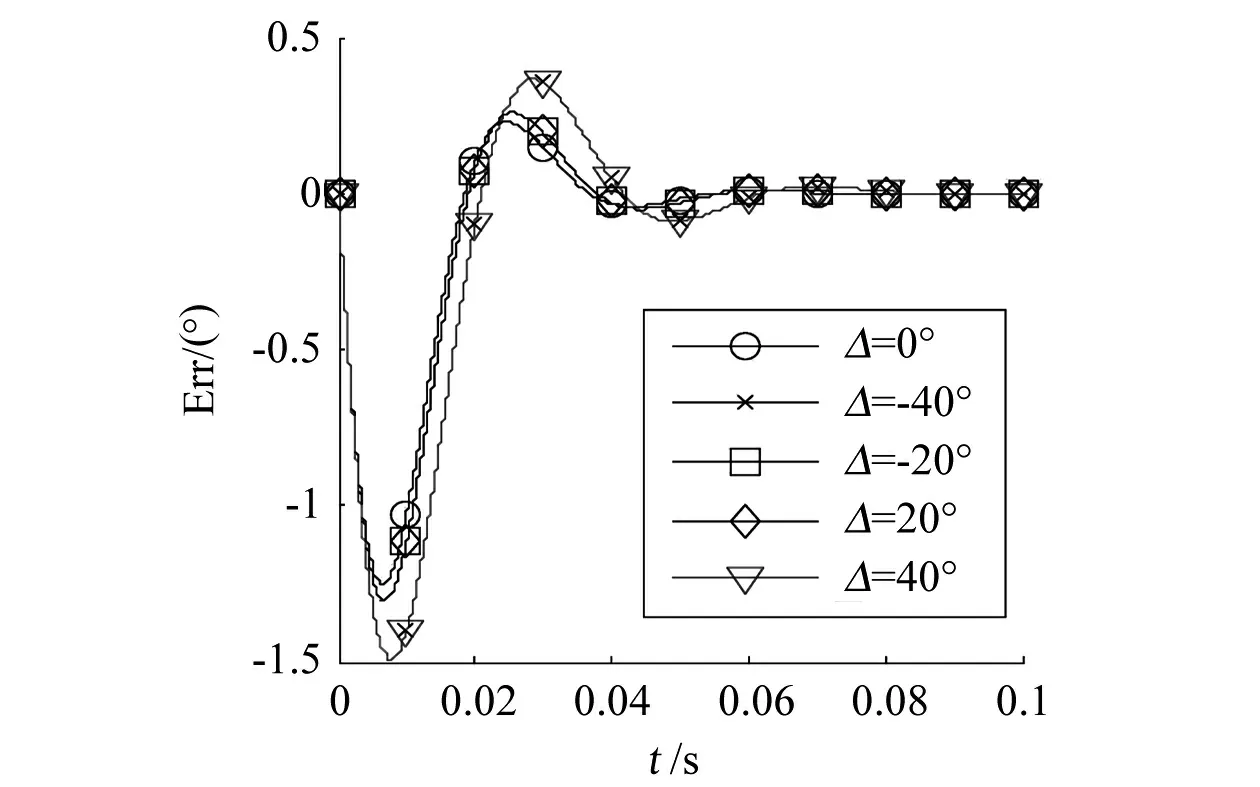
图9 参考信号不同相移误差跟踪曲线局部放大Fig.9 Partial enlargement of tracking diagrams of reference signal different phase shift errors

3.3 电路调幅误差

SIN_C和COS_C端的信号经过放大后，分别为sinθ、(1-k)cosθ，k为一个偏差小量，绝对值不大于0.05。输出为φ，同时考虑2sin2Ωt=1-cos2Ωt，忽略高频信号，则误差函数为

esd=sinθcosφ-(1-k)cosθsinφ=sin(θ-φ)+kcosθsinφ

(14)

令esd=0，同时，当完成跟踪时θ≈φ，由公式(14)可得

sin(θ-φ)+kcosθsinθ=0

所以

(15)

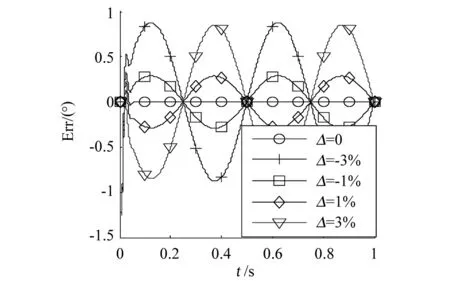
图10 不同幅值偏差下的仿真误差Fig.10 Simulation error under different amplitude deviations

由图10可知，误差绝对值最大点的横坐标为θ=π/4+nπ，n为整数，与公式(15)一致。由表2可看出：理论误差与仿真误差的吻合度很高，最大相对误差为2%，验证了公式(15)。

表2 不同幅值偏差下的理论误差与仿真误差

表2中：k——SIN_C和COS_C的幅值偏差小量；ΔθS——仿真得到的最大误差；ΔθT——公式(15)计算得到的最大理论误差，即公式(15)中θ=π/4；Err——(ΔθS-ΔθT)/ΔθT×100%。

4 结束语

通过引入参考信号，此跟踪算法能够实现系统的稳定跟踪；前置放大电路中，SIN_F、COS_F的相位不同，会造成系统的测量误差为Δθ=arcsin[sin2θ·(1-cosφ)/2]；参考信号的相位误差，在保证相位误差的余弦值符号不发生变化时，会造成系统实际增益变化，但不会直接造成系统的速度跟踪误差，考虑到调相电路的难度，应将该误差绝对值控制在45°内；SIN_F、COS_F的调幅误差，会造成系统的测量误差为Δθ=-arcsin[k(sin2θ)/2]。