基于NSGA-Ⅱ算法的孤岛微电网优化调度
2020-01-05欧阳婷张会林梁毅
欧阳婷 张会林 梁毅


摘 要:针对微电网微电源出力的不确定性,以孤岛微电网运行成本最低、风光消纳比例最大为目标函数,建立孤岛微电网多目标优化调度模型。依据微电网风光出力与负荷供需关系,提高孤岛微电网可再生能源消纳水平,并采用NSGA-Ⅱ算法对调度模型进行求解。以某地区微电网系统典型日为算例,以24小时为周期进行孤岛模式运行。算例结果表明,NSGA-Ⅱ算法调度方案可降低微电网整体成本,提高可再生能源的消纳能力,缓解孤岛微电网在峰谷期间的供电压力。
关键词:孤岛微电网;多目标优化调度;NSGA-Ⅱ算法;MOPSO算法
DOI:10. 11907/rjdk. 201942 开放科学(资源服务)标识码(OSID):
中图分类号:TP319 文献标识码:A 文章编号:1672-7800(2020)011-0184-05
Optimization Scheduling of Island Micro-grid Based on NSGA-ⅡAlgorithm
OUYANG Ting1, ZHANG Hui-lin1,LIANG Yi2
(1. School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093,China;
2. State Grid Jiangxi Electric Power Co., Ltd., Wanan County Power Supply Branch, Jian 343800,China)
Abstract:Because of uncertainty of the source power in the micro-grid, this paper aims to maximize the wind-solar consumption and minimize the cost of the micro-grid, and builds up multi-objective optimization dispatching model of the island micro-grid. According to the supply and demand relation of wind-solar power output and load the renewable energy consumption level of island micro-grid is improved. At the same time, this paper uses the NSGA-Ⅱalgorithm comparing with MOPSO algorithm to solve scheduling model and uses a typical daily micro-grid system in a certain region as an example with a 24h cycle. Finally, the result of the example shows that the scheduling scheme can reduce the overall cost of the micro-grid,improve the absorption capacity of renewable energy, and decrease the power supply pressure of the micro-grid during peak and valley periods.
Key Words: island micro-grid; multi-objective optimization scheduling;NSGA-Ⅱalgorithm;MOPSO algorithm
0 引言
隨着能源互联网和分布式电源技术的发展,微电网优化技术也不断进步[1],在维持电力系统稳定性过程中发挥着重要作用,尤其是在大电网日高峰阶段,可为大电网侧“削峰填谷”,降低电网侧供电压力。微电网运行模式主要为并网与孤岛模式。在用电高峰阶段,离网的微电网缺少了大电网骨干支撑之后,在供电稳定性方面容易受到影响,导致微电网内部资源的控制与管理相对困难,因此对孤岛型微电网调度进行合理调节与优化具有重要意义。
目前已有部分学者对孤岛微电网调度进行了研究。如文献[2]提出一种新型混合能源存储系统(HESS)控制策略,能实现在混合可再生能源系统(HRES)不同组成部分之间保持有功功率平衡;文献[3]考虑经济性、环保性及可靠性,建立了多目标风光柴储微电网优化模型;文献[4]提出对离网微电网进行储能选型与容量配置优化方案。但以上针对微电网的研究都通过改变分布式电源出力或储能控制进行微电网优化,并未提出其它创新方法。
针对微电网调度研究,智能算法是目前普遍应用的方法之一,经典算法包括爬山法、模拟退火、遗传算法以及神经网络等方法。如文献[5]将负荷分为3种类型,并对需求侧负荷进行管理,建立孤岛型微网能量管理混合整数规划模型,并利用CPLEX优化软件进行模型求解;文献[6]研究了风光柴储微电网在并网与孤岛运行方式下的日前优化与实时优化仿真调度,利用爬山法结合遗传算法从电源侧、储能装置的角度对微电网进行优化调度;文献[7]以孤岛微电网系统效益最大化为目标,针对该模型的非凸特性,应用ADMM算法进行模型的分布式优化;文献[8]提出通过(0,1)随机均匀分布改进惯性权重,线性调整认知系数和社会系数结合Levy飞行策略改进鸟群算法,从而优化求解调度模型;文献[9]采用生物地理学算法对运行成本与环保成本最低、用户停电损失最小的微电网多目标优化调度模型进行求解,以提高微电网的经济性、节能型、可靠性;文献[10]提出在微电网孤岛运行模式下采用人工鱼群算法和粒子群算法混合求解微电网模型优化调度方法;文献[11]采用改进粒子群算法优化外点法对孤岛模式微电网进行优化,尽可能避免求解规划时陷入局部极值的问题,同时还考虑了需求侧管理,增加可再生能源的消纳;文献[12]提出电动汽车类可平移负荷参与微电网的调度方案,得出一种计及电动汽车的微电网储能蓄电池容量优化调度模型。以上研究方法说明采用智能算法进行孤岛微电网优化调度具有一定优势。
本文研究孤岛微电网优化调度问题,综合考虑最小化微电网运行成本以及最大化风光消纳比,在微电网孤岛运行模式下建立风力机(WT)、光伏电池(PV)、微型燃气轮机(MT)、蓄电池(BT)微电源模型。同时,采用NSGA-Ⅱ算法求解调度模型,最后通过算例验证本文模型及算法相比其它智能算法,在提高风光消纳和减少运行成本方面具有一定优越性。
1 微电网系统
1.1 PV数学模型
光伏电池输出功率主要受光照强度、工作温度等影响。在当前环境温度下,光伏发电运行管理成本Cpv可表示为:
PPV=PSTCGCGSTC1+K(TC+TSTC) (1)
CPV=t=1TKPV.OMPPV(t) (2)
式中,TSTC、GSTC、PSTC分别为标准测试条件(太阳光入射强度为1 000W/m2,环境温度为25℃)下的光伏额定环境温度、光照强度与发电功率;GC、TC分别为当前光照强度和电池工作温度;K为功率温度系数;KPV.OM为PV单位运行维护成本系数。
1.2 WT数学模型
WT输出功率不仅与自身机组结构有关,大部分WT出力还受到现实生活中风速的限制。风力发电机输出功率与实际风速的关系可近似表示为分段函数[13]:
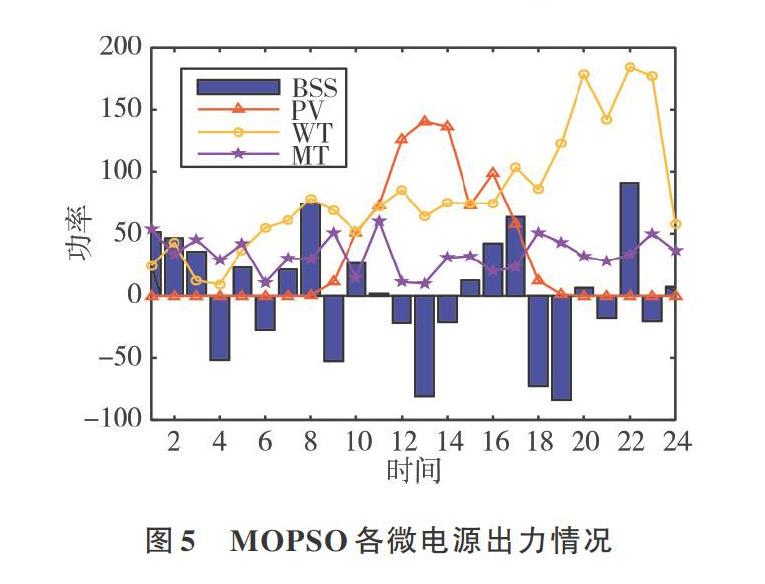
PWT = 0v CWT=t=1TKWT.OMPWT(t) (4) 式中,PN为风力发电机额定输出功率,VN为额定风速;Vci为切入风速,Vco为切出风速;CWT为运行管理成本,KWT,OM为MT单位运行维护成本系数。 1.3 MT数学模型 微电网中当分布式电源和儲能都不能满足负荷需求时,本文采用微型燃气轮机(MT)代表常规机组[14]。MT成本数学模型表示为: CMT=CMT,FUEL+CMT,OM (5) CMT,FUEL=CΔtLHVt=1TPMT(t)ηMT (6) ηMT=0.075 3(PMT65)3-0.309 5(PMT65)2+0.417(PMT65)+0.106 8 (7) CMT,OM=t=1TKMT,OMPMT(t) (8) 式中,CMT为MT总发电成本,CMT,。FUEL为燃料成本,CMT,OM为MT运行管理成本;C为MT燃料气体单价,取2.5元/m3;PMT为MT的出力,LHV为天然气低热值,取9.7 kw·h/m3;ηMT为发电效率,取29%;KMT,OM为单位运行维护成本系数。 1.4 BT数学模型 微电网储能装置可在微电源出力过多时将电能储存起来,微电网供需不足时放电给负荷供电。蓄电池(BT)的荷电状态与电池容量是微电网优化的重要指标[15]。BT的荷电状态SOC与运行管理成本CBT可表示为: SOC(t)=SOC(t-Δt)-Pch(t)ΔtηDSOC(t-Δt)-Pdis(t)Δtηc (9) CBT=t=1TKBT,OMPBT(t) (10) 式中,Pch(t)、Pdis(t)为充、放电功率,ηD、ηD为充、放电效率,CBT为运行管理成本,KBT,OM为单位运行维护成本系数,PBT(t)为BT出力。 2 孤岛微电网优化调度模型 2.1 目标函数 以微电网总运行成本最小化和风光消纳最大化为多目标函数,考虑分布式电源运行管理成本与环境治理成本,微电网总成本CALL的目标函数可表示为: min CALL=CDG+ CE (11) CDG=CPV+CWT+CMT+CBT (12) CE=imjnCijPi(t) (13) 式中,CE为环境治理成本,污染气体种类为CO2、SO2和NOX, Cij为各微电源对应污染气体的治理费用。 2.2 约束条件 2.2.1 功率平衡 PPV+PWT+PMT+PBT=PL (14) 2.2.2 微电源约束条件 PPVmin≤PPV≤PPVmax (15) PWTmin≤PWT≤PWTmax (16) PMTmin≤PMT≤PMTmax (17) 2.2.3 蓄电池约束条件 SOCmin≤SOC≤SOCmax (18) Pchmin≤Pch≤Pchmax (19) Pdismin≤Pdis≤Pdismax (20) 式中,Pchmin、Pchmax分别为充电功率最小、最大值,Pdismin、Pdismax为储能放电功率最小、最大值。 3 模型求解算法 3.1 NSGA-Ⅱ算法介绍 NSGA非支配排序遗传算法主要针对遗传算法求解多目标优化问题,但NSGA算法存在计算复杂性高、计算速度较慢等问题。NSGA-Ⅱ算法相比传统NSGA算法具有以下优势:采用快速非支配排序算法,计算复杂度小于NSGA算法;将父代种群与子代种群合并,使得下一代种群从双倍空间中进行选取,从而保留了最优秀的所有个体;采用拥挤度和拥挤度比较算子,克服了NSGA中需要人为指定共享参数的缺陷,而且准Pareto域中的个体可以扩展到整个Pareto域并均匀分布,保持了种群的多样性;引入精英策略,扩大采样空间,以防最佳个体丢失,提高了算法的运算速度、鲁棒性及计算精度。 3.2 NSGA-Ⅱ算法描述 综上,利用NSGA-Ⅱ算法求解模型最优解主要步骤如下[16]: (1)随机初始化个体数为N的父代种群Pt(初代为 P0),对Pt中的个体进行快速非支配排序,选择父代中优良个体进行交叉、变异,生成与Pt相同规模的子代种群Qt,将子代种群Qt与父代种群Pt合并形成个体数为2N的新种群Rt。 (2)对种群Rt内的个体进行快速非支配排序,对每个个体计算拥挤度,结合个体非支配排序和拥挤度大小筛选出优良的N个个体,形成新的父代种群Pt+1。 (3)选取种群Pt+1内的优秀个体进行交叉、变异,形成新的子代种群Qt+1,再重复以上操作进行新一轮寻优,直到达到最大迭代次数,输出Pareto 最优解集。NSGA-Ⅱ算法流程如图1所示,NSGA-Ⅱ算法仿真如图2所示。 4 算例分析 本文以某地区微电网典型日为例,对微电网进行孤岛运行分析,调度周期为24h。设定BA的SOC初值为0.3,SOC范围为0.2~0.9。该地区PV、WT日输出功率与日负荷预测曲线如图3所示(彩图扫OSID码可见)。各微电源基本参数如表1所示,相应污染排放量及治理费用如表2、表3所示。 采用 NSGA-Ⅱ算法得到各微电源出力情况如图4所示,MOPSO算法的各微电源出力情况如图5所示(彩图扫OSID码可见)。采用NSGA-Ⅱ算法时,在8:00-12:00与18:00-21:00两个负荷高峰阶段,蓄电池放电,燃气轮机相应进行出力,有效缓解了微电网高峰时段的供电压力;在22:00-24:00负荷低谷时段,蓄电池主要进行充电,以储存电能,燃气轮机辅助供电;在0:00-8:00时段,由于光伏和风力发电出力较小,蓄电池和燃气轮机进行放电;同时,在其它平常时段根据负荷和微电源出力情况进行相应充放电。根据微电源出力图,光伏在8:00左右才开始出力,在14:00左右光照最强,出力也最大,在19:00左右结束出力。相比光伏出力,风力发电主要受风速影响,在24小时内均有出力,但在一天的早期时段出力较小,在晚间18:00左右出力增加,在夜间承担大部分微电网出力。NSGA-Ⅱ算法相比于MOPSO算法,其优越性体现在调度方案更为合理,储能充放电更为有序,并能更多地消纳可再生能源。 NSGA-Ⅱ算法与MOPSO算法得到的光伏消纳分别如图6、图7所示(彩图扫OSID码可见)。两种算法光伏消纳功率与总光伏功率趋势基本一致,但NSGA-Ⅱ算法的光伏消纳功率更贴近总光伏功率,光伏消纳比例更高,光伏发电能源利用能力优于MOPSO算法。 同理,NSGA-Ⅱ算法与MOPSO算法得到的光伏消纳分别如图8、图9所示(彩图扫OSID码可见),从中也可得出NSGA-Ⅱ算法的风力消纳比例更高。从表4中可具体看出两种算法的风光消纳比例参数,NSGA-Ⅱ算法光伏消纳比例为93.525%,而MOPSO算法光伏消纳比例为84.23%,同时NSGA-Ⅱ算法风力发电消纳比例为93.182%,MOPSO算法风力发电消纳比例为69.19%。整体来看,NSGA-Ⅱ算法微电网风光消纳比例为93.27%,MOPSO算法风光消纳比例为73.15%。因此,采用NSGA-Ⅱ算法能达到更理想的风光消纳效果,可实现风光消纳最大化目标。 微电网的经济指标主要涉及微电网运行维护成本、燃料成本和污染治理成本。無论是NSGA-Ⅱ算法还是MOPSO算法,在总成本中,燃料成本占较大比例,其次是污染治理成本,而各微电源运行成本相对较低。在运维成本中,光伏发电运维成本最低,燃气轮机运维成本较高,如表5、表6所示。从NSGA-Ⅱ算法与MOPSO算法经济指标对比可以看出,NSGA-Ⅱ算法明显降低了由燃气轮机产生的占比较大的燃料成本。NSGA-Ⅱ算法燃料成本为544.287元,MOPSO算法燃料成本为710.147元,且NSGA-Ⅱ算法其它成本也低于MOPSO算法成本。在总成本方面,NSGA-Ⅱ算法成本为780.996元,MOPSO算法为1 001.96元,如表7所示。所以本文采用的NSGA-Ⅱ算法在经济指标上实现了运行成本最小化目标。此外,在微电网运行过程中应尽量减少燃气轮机类机组,通过最大程度上使用清洁能源能减少一定的污染治理成本,从而有效减少总成本。 5 结语 本文研究了孤岛微电网优化调度问题,针对可再生能源出力的不确性,以风光消纳最大和微电网运行成本最小为目标函数,建立了含光伏、风力、蓄电池和燃气轮机的多目标模型,以孤岛微电网24小时典型日为例,采用多目标NSGA-Ⅱ算法进行优化调度。结果表明,NSGA-Ⅱ算法一定程度上实现了风光消纳比例最大和微电网运行成本最小的目标。下一步研究将考虑把改进NSGA-Ⅱ算法应用于微电网系统,并分析微电网在并网模式下的调度方案是否仍具有优势。
