纳米级碳纤维混凝土材料性能分析
2020-01-05弋楠晁静
弋楠 晁静

摘要:如今,随着各种科学技术的发展,尤其是纳米技术在混凝土领域中的应用,使得混凝土材料不断朝着高性能和高功能方向发展,让混凝土具有更加广阔的应用,同时也促进了建筑行业的发展。作为一种新型建筑材料,纳米级碳纤维混凝土逐步被国内外学者研究,试图提高纳米级碳纤维混凝土的应用效果。文章通过实验分析,研究了几种不同配合比纳米级碳纤维的力学性能,主要包含材料的抗弯强度和劈裂强度。实验结果表明,自密实混凝土比普通混凝土具有更好的抗弯强度和劈裂强度;纳米级碳纤维的分散性越好,越有利于混凝土的力学性能;当纳米级碳纤维的掺量为1.5%左右时,纳米级碳纤维自密实混凝土的劈裂强度最大;当纳米级碳纤维的掺入量大约为1%时,纳米级碳纤维自密实混凝土的抗弯性能最好。
关键词:纳米级碳纤维混凝土;性能;劈裂强度;抗弯强度
中图分类号:TU528
文献标识码:A
文章编号:1001-5922(2020)12-0065-05
在建筑材料中,混凝土属于一种用量最大、用途最广的材料,并且在一定程度上决定着建筑物的质量和安全性[1]。如今,混凝土工程变得愈发复杂、大型化,混凝土材料的性能要求就不断变高[2-3]。传统混凝土会受到诸多因素影响,导致其应用范围受到很大的局限,自从纳米技术在混凝土中的应用,打破了传统混凝土材料的局限性,使得混凝土具有更好的性能,并且想着智能化、多功能化不断发展,极大的促进了混凝土的使用效果和范围[4-5]。纳米级碳纤维混凝土属于一种新型混凝土材料,其中就应用了纳米技术,文章通过对该材料在不同配合比条件下进行实验研究,从而能够更好的了解纳米级碳纤维混凝土材料的力学性能[6]。
1 实验部分
1.1 实验材料和仪器
纳米级碳纤维混凝土材料的主要原材料有纳米级碳纤维、水泥、粗骨料、细骨料、自来水、高效减水剂、消泡剂等,其中纳米级碳纤维的类型比较多,文章选择的纳米级碳纤维的平均直径为150nm,生产过程中使用的改进压实方法,并且是经过低温热处理和氧化处理的纳米级碳纤维。
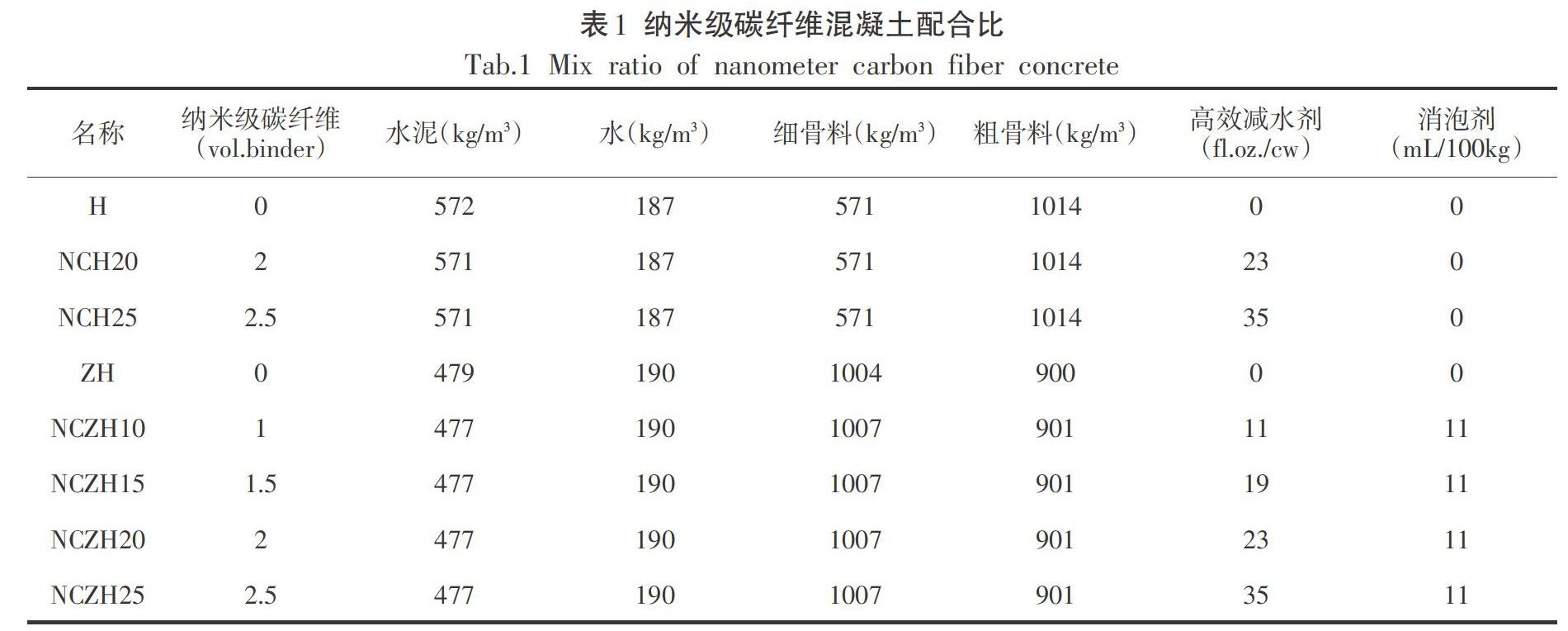
制作纳米级碳纤维混凝土材料所用到的材料比例如表1所示,其中涉及到几种不同的材料比例,H表示的不加入纳米级碳纤维的混凝土,即普通混凝土,目的在于作为对照组。NCH代表的是加入纳米级碳纤维的普通混凝土,ZH代表的是不加纳米级碳纤维的自密实混凝土,NCZH其中的代表的是加入纳米级碳纤维的自密实混凝土,数字代表加入纳米级碳纤维的量。
实验所需要的仪器有万能材料试验机、搅拌机、线性可变差动位移传感器等。
1.2 试样制作
1.2.1 纳米级碳纤维普通混凝土试样的制作
第1步:将自来水和减水剂进行混合为溶液;待用,第2步:再对水泥、粗骨料、细骨料放人离心混凝土搅拌机中进行搅拌均匀;第3步:将纳米级碳纤维加入到溶液中进行高速搅拌,对其进行分散,搅拌时间为3min即可;第4步:将该溶液倒人搅拌机中和干料进行一起搅拌,搅拌时间设置在3 - 5min之间;第5步:对其坍塌度进行检测,当该值处于10 - 20cm之间时才满足试样要求,然后将满足坍塌度要求的混凝土倒人模具中振捣抹平;第6步:对混凝土进行拆模和养护,24h之后即可拆模,另外,需要在水中养护28d。
1.2.2 纳米级碳纤维自密实混凝土试样的制作
第2步:将自来水、减水剂和部分消泡剂进行混合为溶液,待用;第2步和第3步同上;第4步:将剩余的消泡剂和溶液加入到搅拌机中和干料进行混合搅拌,搅拌时间同上;第5步:测量混凝土的表观稳定指标(在0 - 0.5之间)和塌落扩展度(50 - 63cm之间);第6步同上。
1.3 实验介绍
1.3.1 纳米级碳纤维}昆凝土劈裂试验
通过使用万能材料试验机进行测试,其中加载速度设置为250N/s,当试样发生破坏之后停止加载。一共对表1中的8种混凝土进行了实验分析,劈裂实验装置图如图1所示。
1.3.2 纳米级碳纤维混凝土抗弯实验
实验主要针对纳米级碳纤维混凝土在纯弯状态下的抗弯性能进行分析测试,目的在于能够更好的得知混凝土内部应力分布情况。由于是进行抗弯实验,将试样的尺寸设置为一个长方体混凝土梁,对试样进施压时的受力图如图2所示,图2中P表示的是荷载,M表示的是弯矩,V表示的剪力,a为荷载位置,试样通过这种受力情况,在2个P之间的混凝土梁从理论上讲之受到纯弯作用。然后使用万能材料试验机对试样进行实验,其中加载位移速度首先设置为0.25mm/min,当荷载值达到IOOON之后,将其位移速度缩小至0.05mm/min,当试验遭到荷载的破坏之后即停止加载。为了得到实验过程中混凝土的变形,需要在支座处和中间部分安装线性可变差动位移传感器[7]。该实验只对表1中的5种自密实混凝土进行了实验。
在实验过程中弯矩和弯矩比需要通过计算得到,于是梁中心处的弯矩M和最大弯矩Mmax的公式如下所示[8]:
其中a表示的是荷载距离支座的长度,f表示的是混凝土试样的最大抗压强度。
于是可以通过下述公式计算出梁的弯矩比:
2 实验结果和分析
2.1 劈裂试验结果和分析
表2和表3即为8种不同配合比混凝土的平均劈裂强度。为了更加直观的展现出纳米级碳纤维混凝土材料的劈裂强度变化趋势,制作了如图3和图4所示的曲线图,其中图3对应的表2,图4对应的表3。
从表2和图3中可以看出,纳米级碳纤维混凝土和H进行相比较,没有加入纤维混凝土H的劈裂强度更大,并且明显比另外2种纳米级碳纤维混凝土的劈裂強度大,增强率甚至快接近一半,并且还可以看出,当加入的纳米级碳纤维量更多时,混凝土的劈裂强度越低。出现这种现象与纳米级碳纤维的分散性有关,当纤维的量加大时,分散性就会降低,于是就会降低混凝土的劈裂强度。
从表3和图4中可以看出,对于纳米级碳纤维自密实混凝土来将,当加入的纳米级碳纤维量越来越多时,其劈裂强度表现出先增大后降低的趋势,并且相较于没有加入纳米级碳纤维的自密实混凝土,其劈裂强度有所增加,但是增加效果并不显著,最大增强率在7%左右。纳米级碳纤维自密实混凝土的劈裂强度大于ZH,主要原因在于自密实混凝土具有更好的流动性,所以有助于提高纳米级碳纤维的分散性。另外,从图4中可以看出,其中劈裂强度最大时,纳米级碳纤维的掺量为1.5%,所以,为了使得混凝土的劈裂强度最大,将纳米级碳纤维的掺量设置为1.5%比较合适。
通过上述分析表明,自密实混凝土相较于普通混凝土具有更好的流动性,所以能够使得纳米级碳纤维具有更好的分散性,于是其劈裂强度更大,所以当纳米级碳纤维具有更好的分散性时,加入到混凝土中能够提高其劈裂强度。对于普通混凝土,加入过量的纳米级碳纤维并不利于其劈裂强度,反而会适得其反。最后,子纳米级碳纤维自密实混凝土中,纤维掺人量为1.5%时,自密实混凝土的劈裂强度最大。
2.2 抗弯试验结果和分析
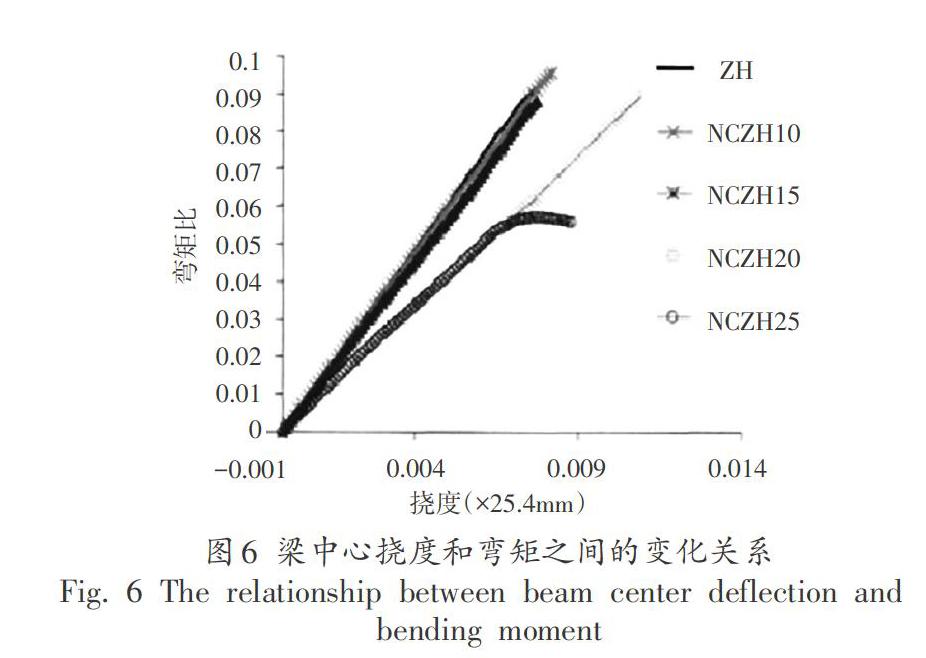
由于纳米级碳纤维自密实混凝土材料的劈裂强度更大,于是研究材料的抗弯能力时没有对纳米级碳纤维普通混凝土材料进行实验分析。完成纳米级碳纤维自密实混凝土的抗弯实验之后,获得5种不同配合比下混凝土梁中心挠度的变化,图5表示的是挠度和荷载之间的关系,图6表示的是挠度和弯矩之间的关系。
从图5和图6中可以看出,在自密实混凝土中加入纳米级碳纤维时,能够提高材料的抗弯性能。当纳米级碳纤维掺人量为1%时,相较于不含纳米级碳纤维的自密实混凝土,其挠度增加超过了50%,并且在其他3个配合比中具有最好的抗弯强度和延展性。当纳米级碳纤维掺人量增加时,材料的抗弯性能有所降低,但是相比于ZH,NCZH15、NCZH20、NCZH25的延展性还是有所增强,只是没有NCZH10增长得明显。所以当纳米级碳纤维的掺人量比较多时,并不会有利于增强混凝土材料的性能,反而会降低混凝土自身强度。
实验过程中获得混凝土最大承载能力和最大挠度的值如表4所示,从中可以明显的看出,当纳米级碳纤维的掺入量为1%时,此时梁中心最大挠度最大,相较于没有加入纳米级碳纤维的自密实混凝土,提高了达到了56%左右。
通过上述对纳米级碳纤维自密实混凝土材料的抗弯实验可知,当选择的纳米级碳纤维具有很好的分散性时,加入到自密实混凝土材料中能够提高材料的抗弯性能。另外,当纳米级碳纤维掺人量较多时,会降低材料的抗弯性能。最后,当纳米级碳纤维的掺入量大约为1%时,此时纳米级碳纤维自密实混凝土的抗弯性能最好。
3 结语
纳米级碳纤维混凝土材料包含多方面的性能分析,文章只对其力学性能中的劈裂和抗弯进行了实验研究,由于纳米级碳纤维加入到2种不同混凝土中,自密实混凝土比普通混凝土能够让纤维具有更好的分散性,于是能够提高纳米级碳纤维混凝土材料的劈裂强度和抗弯强度;当纳米级碳纤维加入量过多时,就会导致其在混凝土中分散性降低,就会影响到混凝土的性能,所以加入的纳米级碳纤维需要适量才有利于材料性能提高。从实验结果可知,当纳米级碳纤维掺入量为1.5%时,自密实混凝土的劈裂强度最大,当纳米级碳纤维的掺人量大约为1%时,此时纳米级碳纤维自密实混凝土的抗弯性能最好。所以,总之,纳米级碳纤维混凝土材料中如果能够提高纳米级碳纤维的分散性,那么就能够提高混凝土材料的基本物理力学性能。
参考文献
[1]潘晓璐.浅析外加剂对混凝土的影响[J].城市建设理论研究(电子版),2012(03):1-4.
[2]吴中伟.绿色高性能混凝土一混凝土的发展方向[J]混凝土与水泥制品,1998(1):3-6.
[3]冯乃谦,高性能混凝土与超高性能混凝土的发展和应用[J].施工技术,2009(04):5-10.
[4]梁晖,刘国军.现代混凝土中的纳米技术[J].建筑技术开发,2005,032(07):46-48.
[5] Anjan K CHATTERJEE.纳米技术和可持续发展混凝土:独特的新兴组合[J].硅酸盐学报,2015,43(10):1385-1395.
[6]姚斌.环境因素对纳米碳纤维混凝土压敏特性的影响[D].黑龙江:哈尔滨工业大学,2013.
[7]谭永宏,曾喆昭.基于Laguerre多项式的LVDT位移传感器非线性校正[J].传感器与微系统,2016,35(9):104-105.
[8]鄭文忠,张格明,王英,柱支承板变形计算的双向板带叠加法及裂缝验算建议方法[J].工业建筑,2006,36(11):52-55.
