一种最优自适应增益非线性观测器的锂电池SOC估算方法

鲍时全 李正明

摘 要：如今电动汽车的发展十分迅速，其动力电池荷电状态SOC关系到锂电池及整车系统的安全、可靠运行，因为SOC表明了电池剩余电量。由于SOC是一个不可直接测量的非线性变量，因此设计一种精度高、可行性强的算法具有十分重要的意义。提出一种最优自适应增益非线性观测器（OAGNO），用差分进化算法（DE）对观测器参数进行寻优。为了验证该方法的先进性，对型号为NCR18650GA的三元锂电池进行工况实验，结果表明，相比无迹卡尔曼滤波（UKF），最优自适应非线性状态观测器具有更高的精度，误差在3%左右。

关键词：电动汽车;荷电状态;无迹卡尔曼滤波;最优自适应非线性观测器;差分进化算法

DOI：10. 11907/rjdk. 201338                                                                  开放科学（资源服务）标识码（OSID）：

中图分类号：TP301   文献标识码：A                 文章编号：1672-7800（2020）011-0060-06

A State of Charge Estimation Method of Lithium-ion Battery

Based on Optimal Adaptive Gain Nonlinear Observer

BAO Shi-quan，LI Zheng-ming

（School of Electrical and Information Engineering， Jiangsu University， Zhenjiang 212000，China）

Abstract： Electric vehicles are developing rapidly nowadays， and the state of charge of power battery is related to the safe and reliable operation of lithium battery and whole vehicle system， because the SOC indicates the remaining power of the battery. Since SOC is a non-linear variable which can not be measured directly， it is very important to design an algorithm with high precision and strong feasibility. In this paper， an optimal adaptive gain nonlinear observer for SOC estimation of lithium-ion batteries is proposed，parameters of observer is selected by using a differential evolution algorithm. In order to verify the progressiveness of this method， the operating conditions of a ternary lithium-ion battery with model NCR18650GA are tested. The results show that the proposed optimal adaptive nonlinear observer has higher accuracy than unscented Kalman filter， and the SOC estimation error is about 3 percent.

Key Words： electric vehicle;state of charge; unscented Kalman filter; optimal adaptive gain nonlinear observer; differential evolution

0 引言

鋰电池由于具有能量密度较高、无记忆性、循环寿命长、自放电率低并且清洁环保的优点[1]，在储能系统中受到越来越多的关注，特别是在新能源汽车中应用广泛。然而，为保证锂电池能够安全、可靠地工作，对电池管理系统（Battery Management System，BMS）要求很高。BMS负责检测电池工作时的参数，如电流、电压、温度等，并估算电池状态量，如荷电状态SOC（State of Charge）、健康状态SOH、功率状态SOP。SOC的定义是电池剩余容量与额定容量之比，决定了电池在充电之前可以使用的时间，对SOC的估算是BMS最关键的任务之一。

为精确估算电池SOC，国内外很多学者展开了深入研究，并提出了很多方法，比如开路电压法[2]、内阻法[3]、安时积分法[4]、神经网络法[5-7]、卡尔曼滤波法[8-10]、粒子滤波法[11-13]、滑模观测器法[14-16]等。前4种方法不需要特地建立电池模型，所以又称为非模型方法。开路电压法作为一种最简单的SOC估算方法，可利用电池开路电压与SOC之间的函数关系，通过测量开路电压估算SOC，但电池开路电压需要静置的时间太长，不适合SOC在线估算;内阻法利用电池内阻与SOC之间的函数关系，通过欧姆定律计算出电池内阻进而得到SOC，但电池内阻容易受到温度影响，并且电动汽车行驶过程中电流变化很大，对电池内阻的计算十分不利，因此内阻法基本上不适用;安时积分法过度依赖于初始SOC值与电流测量精度，并且因为含有积分项，又未引入闭环反馈，估计误差会随着时间的积累变得越来越大，因此工程中需要经常与其它算法结合使用;神经网络法需要大量样本数据训练网络，并且对芯片的数据处理能力有很高要求，增加了BMS的硬件成本，适合于实验室研究，工程应用中很少见。

后3种方法是基于模型的闭环估算方法，需要对电池进行建模，得到电池系统的状态空间方程，然后通过算法估算出SOC。Plett分别于2004与2006年提出用扩展卡尔曼滤波（Extended Kalman Filter，EKF）和无迹卡尔曼滤波（Unscented Kalman Filter，UKF）估算电池SOC，尽管能获得足够的精度，但也存在一定不足：例如EKF采用Taylor展开式近似模拟非线性系统，为简化运算，常忽略二次及以上的高阶展开项，从而影响估算精度。此外，EKF还需要计算Jacobian矩阵，计算量较大，并且当系统非线性程度较高时，甚至会出现“滤波发散”的情况。文献[17]表明，相比于EKF，UKF的估算精度更高，鲁棒性更强，然而代价是大量矩阵运算会耗费更多时间，且对硬件要求更高。此外，基于卡尔曼滤波的方法还要求系统噪声是高斯白噪声，并对电池模型精度要求较高，这两点在实际情况中并不容易实现。粒子滤波可用于高阶非线性电池系统遭受非高斯扰动时的SOC估计，但其硬件实现是一个巨大的挑战，因为粒子滤波需要大量样本，并进行矩阵操作。滑模观测器是一种基于现代控制理论的估算方法，针对电池模型的不确定性及外界扰动具有很好的鲁棒性，但通常很难制定出最优观测器参数，如不确定性边界和开关增益。此外，滑模观测器要求电池系统的观测方程是线性的，意味着需要用线性拟合方法拟合出开路电压与SOC之间的关系，显然会增加SOC估计误差。

综上所述，现有各种方法都有自己的优缺点。本文提出一种最优自适应增益非线性觀测器（Optimal Adaptive Gain Nonlinear Observer， OAGNO）的方法对电池SOC进行估算。首先建立电池二阶等效电路模型模拟锂电池动态特性，采用基于脉冲电流放电过程的电压响应和指数函数拟合方法确定电池模型参数，然后设计自适应增益非线性观测器，并用差分进化算法（Differential Evolution，DE）对自适应增益进行寻优，达到最小化估算误差的效果。

1 电池建模

1.1 SOC定义

通常，SOC被定义为电池剩余容量与额定容量之比，如式（1）表示。

SOC=SOC0-0tηiLQNdt （1）

式中，SOC0表示SOC初始值;QN是电池额定容量;η是库伦效率，表示电池放电容量与充电容量之比;iL是负载电流，放电为正，充电为负。

1.2 电池等效模型建立

文献[18]对12种锂电池等效电路模型进行对比分析，结果表明采用复杂的电气模型可以提高模型精度，但计算复杂度和计算成本也会成倍提升。考虑到建模误差和计算成本，本文采用常用的二阶RC等效模型，如图1所示。其中，Uoc表示电池开路电压，Uoc与电池SOC之间有非线性函数关系，R0表示电池欧姆内阻，R1、R2分别表示电池第一极化电阻和第二极化电阻，C1、C2分别表示电池第一极化电容和第二极化电容，U1、U2分别表示第一、第二个RC环节电压，Uout是电池端电压。

由KCL和KVL可得电池二阶RC模型状态方程为：

IL=C1dU1dt+U1R1IL=C2dU2dt+U2R2Uout=Uoc-IL？R0-U1-U2 （2）

将式（1）、式（2）表示为状态空间方程的形式：

x=Ax+Buy=h（x）+Du （3）

式中：

x=U1U2SOCT，y=Uout，u=ILA=-a1000-a20000=-1/R1C1000-1/R2C20000B=1C11C2-1/QN，D=-R0h（x）=Uout（SOC）-U1-U2 （4）

2 电池模型参数辨识

确定电池模型后，在进行SOC估算前还需对电池参数进行辨识，即获得R0、R1、R2、C1和C2数据，相关参数都会随SOC的变化而改变，辨识结果对接下来的SOC估算工作很重要。本文采用基于脉冲放电实验的方法进行离线参数辨识，共进行20次脉冲放电，每次脉冲放电SOC减少5%，然后采集不同SOC处的电池端电压，通过指数拟合的方法计算出R0、R1、R2、C1和C2。比如在SOC=70%处，辨识出的参数为：

R0=0.032 34Ω，R1=0.017 14Ω，R2=0.011 32Ω，C1=1 650F，C2=146 500F。具体步骤和方法在文献[19]中有详细介绍，这里不再赘述。

另一方面，能较为准确地反映电池开路电压OCV与SOC的函数关系对于SOC的精确估算大有裨益。基于上述脉冲放电实验，获得的部分数据如表1所示。

在MATLAB中，用polyfit进行幂函数多项式拟合，阶数设置为6，得到的函数关系式如下：

式中，CR是交叉概率，rand（0，1）是在（0，1）區间均匀分布的随机数，jrand为1，2，？？，D的随机整数。

（3）选择操作：在父代个体与中间个体之间根据适应度函数选择能进入下一代的个体。

xi（g+1）=ui（g+1），iffui（g+1）≤fxi（g）xi（g）otherwise （25）

式中，f是适应度函数。因为估计精度是锂离子电池SOC估计中最重要的一个问题，定义如下误差组合作为差分进化算法的适应度函数。

FT=2eMAE+emax （26）

式中，eMAE、emax分别表示平均绝对误差和最大误差。因为平均绝对误差的参考价值大于最大误差，所以在适应度函数中将eMAE的权重系数设置为emax的两倍。eMAE定义如下：

eMAE=k=1NSOCk-SOCkN （27）

式中，SOCk、SOCk分别表示第k次时间步长中SOC的实际值和估计值，总步数为N。

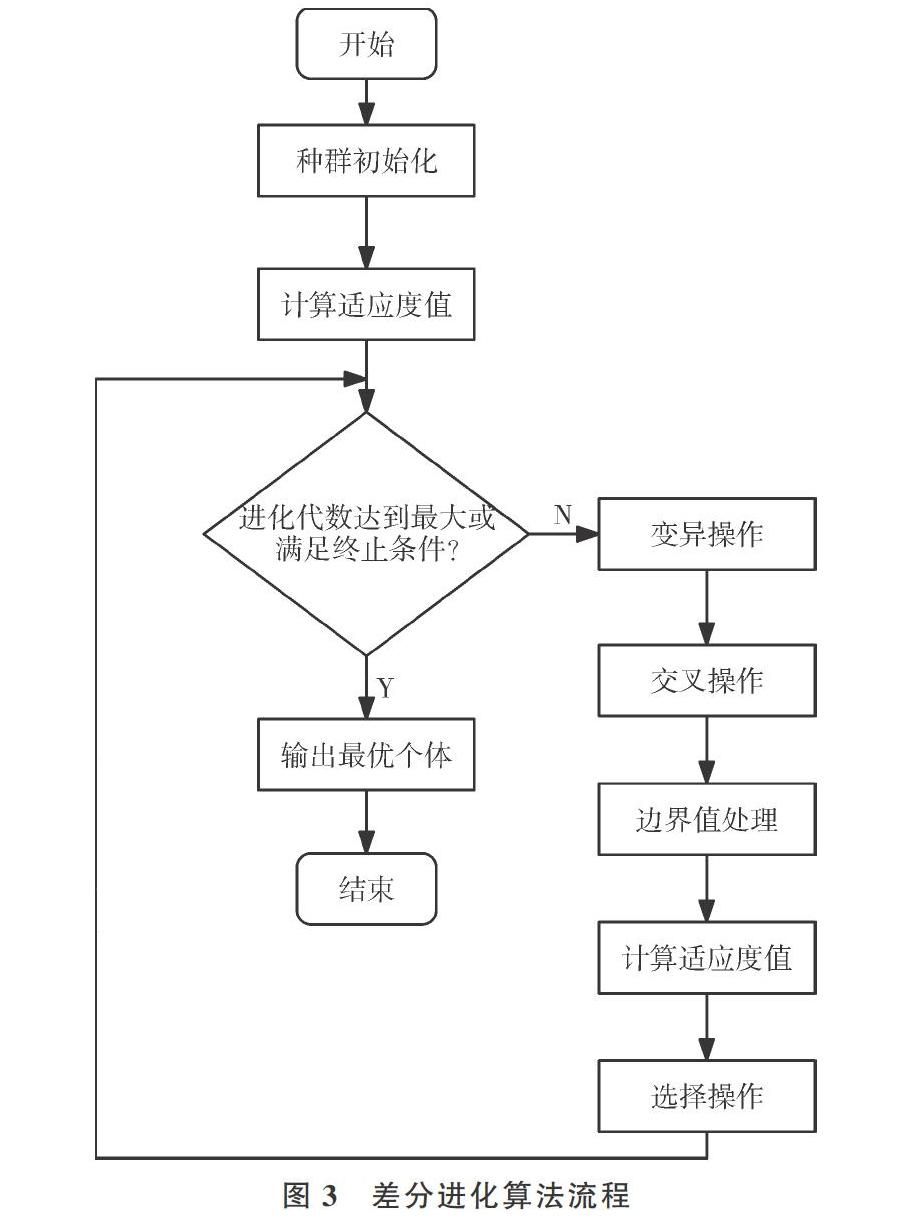
本研究中通过最小化式（26）中FT的值，选择λi、α和β，流程如图3所示。

具体步骤如下：

（1）初始化种群控制参数。包括设置种群大小NP、算法最大迭代次数G、缩放因子F、交叉概率CR和染色体基因边界xUj，i、xLj，i。

（2）由式（28）随机产生初始化种群。

xj，i（0）=xLj，i+rand（0，1）？（xUj，i-xLj，i） （28）

（3）计算初始化种群中每个个体的适应度值。

（4）判断是否达到终止条件或进化代数达到最大。若是，则终止进化，将得到的最佳个体作为最优解输出;若否，则继续下面步骤。

（5）进行变异、交叉操作，得到中间种群。

（6）判断中间种群中是否有向量超过边界xUj，i、xLj，i的设定。若超过边界，则分别用xUj，i、xLj，i代替。

（7）计算当前种群和中间种群的适应度值并进行选择，得到新一代种群。

（8）进化代数g=g+1，转步骤（4）。

4 实验分析

4.1 实验平台

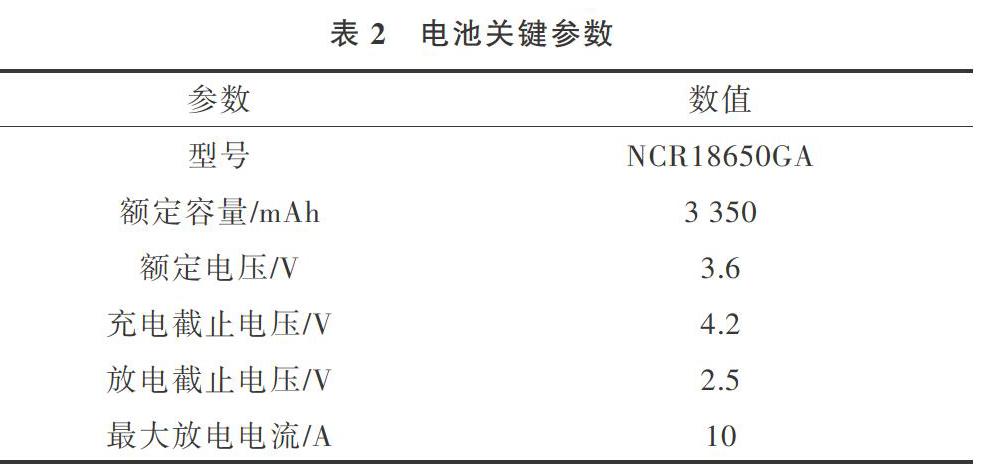
为验证所提出的最优自适应非线性观测器的有效性与先进性，采用NEWAREBTS4000电池测试仪对型号为NCR18650GA的三元锂电池进行测试，其电流和电压测量精度可达0.1%，并将测试数据导入MATLAB中进行SOC估算。表2是电池NCR18650GA的关键参数。

表2 电池关键参数

参数         数值         型号         NCR18650GA  额定容量/mAh        3 350        额定电压/V     3.6   充电截止电压/V     4.2   放电截止电压/V          2.5   最大放电电流/A     10

4.2 自适应增益非线性观测器参数寻优结果

为模拟电动汽车在道路上行驶时电池的负载特性，进行NEDC动态工况实验[23]，工况电流和电压数据如图4、图5所示。

在用DE寻优观测器增益参数前，先设置DE的参数，具体如表3所示。

自适应非线性观测器参数优化的目的是最小化式（26）中的适应度函数，其适应度函数收敛过程如图6所示。可以看到，当迭代次数达到28时，所提出的组合误差收敛到最小，约为3.6%，最终观测器参数λ1，λ2，λ3，α，β收敛到21.0，0.1，1.5，0.3，1.8。

4.3 SOC估算结果分析

为评估所提出最优自适应增益非线性观测器的电池SOC估算性能，将其估算结果与UKF估算结果进行对比，基于UKF的SOC估算已被证明在精度与鲁棒性方面效果较好。图7是两种方法SOC估算结果与实际SOC曲线，实际SOC曲线是基于安时积分法得到的。图8是SOC估算误差。

从图7可以看到，UKF与本文提出的最优自适应增益非线性观测器都能很好地估算出电池SOC。两者相比，最优自适应增益非线性观测器的性能更优。

从图8可以看出，UKF的估算误差在4%左右，最大估算误差为4.29%，其均方根误差RMSE的值为1.69%;最优自适应增益非线性观测器估算误差在3%左右，最大估算误差为3.31%，其均方根误差RMSE的值为1.40%。

因此，本文提出的最优自适应增益非线性观测器的性能优于UKF，可满足电动汽车动力电池SOC的估算需求。

5 结语

本文基于电池的二阶RC等效模型和离线参数辨识，设计出自适应增益非线性观测器，并证明了观测器的收敛性。在此基础上利用差分进化算法对自适应增益进行寻优，即得到最优自适应增益非线性观测器。实验结果表明，本文方法相较于UKF，估计精度更高，因为基于UKF的估算仍不能克服卡尔曼滤波对系统模型精度要求高，以及系统噪声统计特性已知的缺点，而最优自适应增益非线性观测器没有这方面的要求，且计算量小于UKF。本文提出的电池SOC估算方法的缺点在于使用的差分进化算法在参数设置不当时会出现早熟现象，容易陷入局部最优点。下一步研究重点将放在如何避免差分算法的早熟方面，从而达到更高的SOC估算精度。

参考文献：

[1] LU L，HAN X，LI J， et al. A review on the key issues for lithium-ion battery management in electric vehicles[J].  Journal of power sources， 2013， 226：272-288.

[2] LEE S，KIM J，LEE J，et al. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge[J].  Journal of Power Sources， 2008， 185（2）：1367-1373.

[3] DUBARRY M，SVOBODA V，HWU R，et al. Capacity loss in rechargeable lithium cells during cycle life testing： the importance of determining state-of-charge[J].  Journal of power sources， 2007， 174（2）： 1121-1125.

[4] 鲍慧，于洋. 基于安时积分法的电池SOC估算误差校正[J]. 计算机仿真， 2013（11）：154-157，165.

[5] LI I H，WANG W Y，SU S F，et al. A merged fuzzy neural network and its applications in battery state-of-charge estimation[J].  IEEE Transactions on Energy Conversion， 2007， 22（3）：697-708.

[6] 孙弘利，赵冠都. 基于ELM神经网络的磷酸铁锂电池SOC估算研究[J]. 通信电源技术， 2018， 35（9）：75-77.

[7] 夏克刚，钱祥忠，余懿衡， 等. 基于BP神经网络的锂电池SOC在线精确估算[J].  电子设计工程， 2019， 27（5）：67-71，82.

[8] PLETT G L.  Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs part 2 modeling and identification[J].  Journal of power sources， 2004， 134（2）： 262-276.

[9] 谢中灿.  扩展卡尔曼滤波在锂电池SOC估算中的应用[J].  化工设计通讯， 2018， 44（11）：149-151，168.

[10] ZHIGANG H，DONG C，CHAOFENG P，et al. State of charge estimation of power Li-ion batteries using a hybrid estimation algorithm based on UKF[J].  Electrochimica Acta， 2016， 211：101-109.

[11] DU J N，WANG Y Y，WEN C Y.  Li-ion battery SOC estimation using particle filter based on an equivalent circuit model[C]. IEEE International Conference on Control & Automation. IEEE， 2013：580-585.

[12] WANG Y，ZHANG C，CHEN Z. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter[J].  Journal of Power Sources， 2015， 279：306-311.

[13] 潘俊铖.  基于粒子滤波的锂电池SOC估算及单体一致性评价研究[D]. 绵阳：西南科技大学，2017.

[14] CHEN X，SHEN W，CAO Z，et al. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles[J].  Journal of Power Sources， 2014， 246：667-678.

[15] 孙冬， 陈息坤.  基于离散滑模观测器的锂电池荷电状态估计 [J].  中国电机工程学报， 2015（1）：185-191.

[16] 杨立.  基于二阶离散滑模观测器的锂电池SOC估计[J].  电器与能效管理技术， 2018 （3）： 43-46.

[17] LI J，KLEE BARILLAS J，GUENTHER C，et al. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles[J].  Journal of Power Sources， 2013， 230：244-250.

[18] HU X， LI S， PENG H.A comparative study of equivalent circuit models for Li-ionbatteries[J].  Journal of Power Sources ，2012 ，198 ：359-367.

[19] GHOLIZADEH M，SALMASI F R.  Estimation of state of charge， unknown nonlinearities， and state of health of a lithium-ion battery based on a comprehensive unobservable model[J].  IEEE Transactions on Industrial Electronics， 2014， 61（3）：1335-1344.

[20] JOHANSSON A，MEDVEDEV A. An observer for systems with nonlinear output map[J]. Automatica， 2003， 39（5）：909-918.

[21] 楊启文， 蔡亮， 薛云灿.  差分进化算法综述[J].  模式识别与人工智能， 2008， 21（4）：506-513.

[22] HUY A H P，NGOC S N，CAO V K，et al. Parameter identification using adaptive differential evolution algorithm applied to robust control of uncertain nonlinear systems[J].  Applied Soft Computing， 2018， 71：672-684.

[23] 刘存山.  基于NEDC工况的动力电池使用寿命测试方法研究[J].  电源技术， 2017（11）：47-49.

（责任编辑：黄 健）