融合Markov与BP神经网络的纯电动汽车销售量预测研究

石翠翠 刘媛华

摘 要：随着纯电动汽车市场的不断扩大，对销售量的精确预测成为人们当前关注的热点。提取影响销售量的7个关键因素以及2017～2019年9月的纯电动汽车销售量，首先利用BP神经网络模型对33个月的数据进行測试，并用训练好的模型预测2019年1～9月销售量，再利用马尔科夫（Markov）模型将BP神经网络模型预测的相对误差划分为6种状态，对预测结果进行修正。通过对BP神经网络模型与Markov-BP神经网络模型预测结果进行对比检验，发现Markov-BP神经网络的预测准确度更高，表明采用Markov-BP神经网络模型对纯电动汽车月度销售量进行预测具有一定现实意义。

关键词：BP神经网络;马尔科夫链;纯电动汽车;销售量预测;MATLAB

DOI：10. 11907/rjdk. 201180                                                                  开放科学（资源服务）标识码（OSID）：

中图分类号：TP306   文献标识码：A                 文章编号：1672-7800（2020）011-0050-04

Pure Electric Vehicle Sales Forecast Research Based on

Markov and BP Neural Network

SHI Cui-cui， LIU Yuan-hua

（Business School， University of Shanghai for Science & Technology， Shanghai 200093， China）

Abstract：With the continuous expansion of the pure electric vehicle market， the accurate prediction of sales volume has become the focus of attention. Seven key factors affecting the sales volume and the sales volume of pure electric vehicles in the 33 months from 2017 to 2019 are extracted. Firstly， the data of these 33 months are tested by BP neural network model， and the sales volume from January to September in 2019 is predicted by the trained model. Then， the relative error of BP neural network model is divided into six states by using Markov model. The result is modified to get the forecast of pure electric vehicle sales volume based on Markov modified BP neural network （BPMC）. Through the comparative test， it is verified that the prediction accuracy of Markov correction is higher， which shows that the BPMC model has a certain practical significance for the monthly sales forecast of pure electric vehicles.

Key Words：BP neural network; Markov chain; pure electric vehicle; sales forecast; MATLAB

0 引言

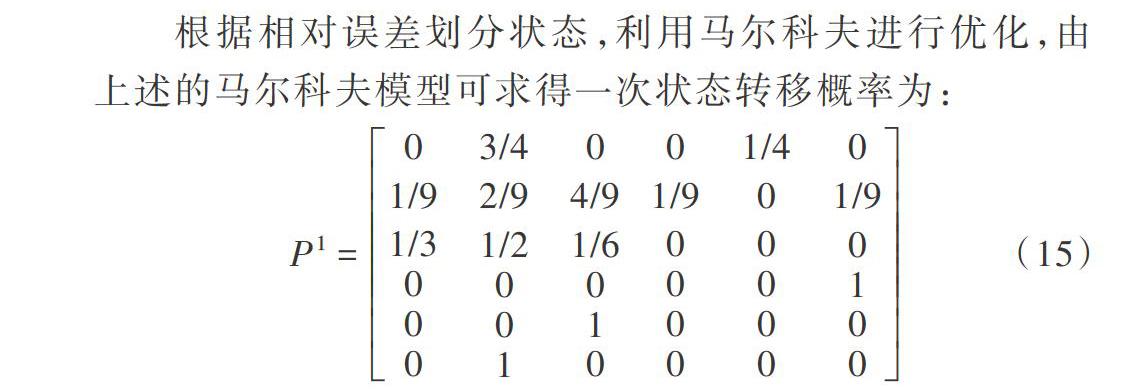
纯电动汽车的应用可以缓解能源短缺、环境污染等问题，因此各企业越来越重视纯电动汽车生产、技术和销售方面的创新。纯电动汽车销售量也日益增长，根据前瞻产业研究院报告显示，2019年上半年纯电动汽车全球销售量增长了92%，达到76.5万辆，中国市场销售量为43.07万辆，同比增长了111%。由销量数据可以看出，纯电动汽车市场发展前景是可观的。因此，纯电动汽车研发与推广依然是新能源汽车重要的研究方向。近年来在政府与企业的共同努力下，电动汽车在生产成本、行驶里程、资金投入与使用等关键问题上获得了重大突破[1]。对纯电动汽车月度销售量进行预测，能为企业科学制定汽车产量提供依据。

影响电动汽车销售量的因素众多，且复杂多变，通常具有非线性变化特性，导致传统线性映射模型对纯电动汽车销售量的预测精度较低[1]。因此，很多学者采用基于非线性模型的预测方法。如董丽丽等[2]利用LSTM神經网络对煤矿突水情况进行预测;刘璐等[3]利用SVM对烟草销售量进行预测等。为了实现更好的预测效果，将多种预测方法相结合也成为当前的研究热点[4-5]。如李军怀等[6]提出借助马尔可夫链修正指数平滑的方法预测短时交通流量，以提高预测精度;黄羹墙等[7]首先利用BP神经网络模型对短期电价进行初步预测，再用马尔可夫模型对预测误差进行修正，可提高短期电价预测精度;石萍等[8]考虑电动汽车销量的季节性变化因素，运用组合模型预测新能源电动汽车销售量;周彦福等[9]先利用灰色关联分析8种影响销售量的因素，再构建果蝇算法优化灰色神经网络（FOA-GNN）预测模型进行新能源汽车月度销售量预测，通过对比预测结果，显示该模型具有较高的预测精度。

在之前的研究中，提取纯电动汽车销售量影响因素时并未考虑消费者预期指数、消费者满意指数、企业家信心指数和煤油电价格指数等因素，本文将这些因素考虑在内，利用BP神经网络预测纯电动汽车销售量，再根据马尔科夫链修正预测结果，以进一步提高预测精度。

1 BP神经网络与马尔科夫模型

1.1 BP神经网络模型

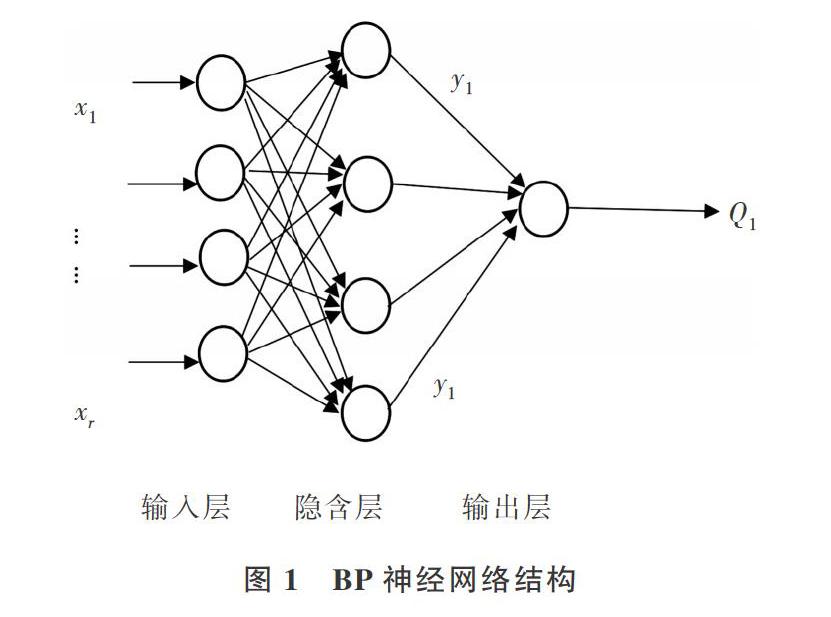
BP神经网络是1986年由以Rumelhart&McCelland为首的科学家小组提出的，是一种利用误差逆传播算法训练的多层前馈网络，因其具有简单易行、计算量小、并行性强等优点，成为目前应用比较广泛的一种神经网络模型[10-11]。BP神经网络由输入层、隐含层和输出层组成（见图1）。在网络训练过程中，通过将输出层与实际输出样本之间的误差经过各隐含层反向传递到输入层，逐层计算各层神经元误差，然后根据误差梯度下降法调节各层权值和阈值，使修改后网络最终输出能接近期望值[12-14]。

1.1.1 信号前向传播过程

设网络输入模式为xx1，x2，…，xnT，隐含层有h个单元，其输出为y=（y1，y2，…，yh）T，输出层有m个单元，其输出为z=（z1，z2，…，zm）T，目标输出为t=（t1，t2，…，tm）T，隐含层到输出层的传递函数为f，输出层传递函数为g。计算公式如下：

yj=fi=1nwijxi-θ=fi=0nwijxi         （1）

式中，yj表示隐含层第j个神经元的输出，w为权重向量，w0j=θ，x0=-1。f为激活函数，一般选取s型函数。

fx=11+e-ax，（0

zk=g（j=0hwjkyj）          （3）

式中，zk表示输出层第k个神经元的输出。此时网络输出与目标输出的误差为：

ε=12k=1m（tk-zk）2                        （4）

由于负梯度方向是函数值减小最快的方向[11]，因此可设定一个步长η，每次沿负梯度方向调整η个单位，即每次权值的调整为：

Δwpq=-η？ε？wpq                            （5）

其中，η为学习速率。

1.1.2 误差反向传播

隐含层到输出层的权值调整迭代公式为：

wjkt+1=wjkt+ηδkyj                 （6）

从输入层到隐含层的权值调整迭代公式为：

wijt+1=wijt+ηδjxj                  （7）

1.2 马尔科夫链预测模型

马尔科夫过程用于研究一个系统的状况及其转移，是一种常见的简单随机过程。其通过对不同状态初始概率以及状态之间转移概率的研究，确定状态变化趋势，从而达到预测未来的目的[10]，具有无后效性、遍历性和过程随机性。应用马尔科夫（Markov）模型对BP神经网络模型预测数据进行处理，可提高预测精度。

1.2.1 马尔科夫链

时间和状态都是离散的马尔科夫过程称为马尔科夫链[10]。假设马尔科夫链有n个状态，则状态概率向量为α=α1，α2，…，αn，公式为：

αn=α0pn          （8）

式中，αn、α0分别表示n时刻和初始时刻的状态概率向量，p表示状态转移概率矩阵。

1.2.2 初始状态概率与状态转移概率矩阵

（1）初始状态概率。用Mi表示Ej型状态出现的总次数，则初始概率为：

α（0）i≈Fi=Mii=1nMi（i=1，2，…，n）          （9）

（2）状态转移概率。如果研究对象处于Ei，下一步转移到Ej，此过程共发生nij次，则：

pij=nijni，i，j=1，2，…，n

0≤pij≤1，j=1npij=1             （10）

（3）状态转移概率矩阵。根据状态转移概率得出状态转移概率矩阵为：

P=P11P12？P1nP21P22？P2n？Pn1？Pn2？？？Pnn，

0≤pij≤1，j=1npij=1                            （11）

1.2.3 马尔科夫链修正BP神经网络预测值

将BP神经网络预测值与实际值的相对误差划分为不同状态，αn为时刻n的状态概率向量，αn中最大概率值对应的状态Ej为预测时刻所对应的状态，则修正后的预测结果为：

e*=ea+eb2                      （12）

Q*=Qx（1+e*）                 （13）

式中，ea、eb為状态区间上下界，Qx为BP神经网络预测的纯电动汽车销售量。

2 数据来源及预处理

数据样本的选取是影响BP神经网络模型预测结果的关键因素，因此选取纯电动汽车销售量的影响因素要与纯电动汽车销售量具有高相关性。煤油电价格指数和中国汽油价格可反映纯电动汽车销售趋势，居民消费价格指数可反映居民消费水平的高低，消费者满意指数与预期指数代表着消费者的满意度与期望，企业家信心指数影响企业管理模式与电动汽车产销模式，这些因素都能综合反映纯电动汽车销量情况。因此，本文选取中国居民消费价格指数、煤油电价格指数、消费者满意指数、消费者预期指数、消费者信心指数、中国汽油价格、企业家信心指数作为影响纯电动汽车销售量的主要因素。

本文通过东方财富网数据中心搜集到2017年1月-2019年9月各影响因素相关数据，并在前瞻产业研究院查询到33个月份的纯电动汽车销售量。采取的样本数据中各因素评价标准不同，通常具有不同的量纲和数量级，需要对原始数据进行标准化处理以确保结果的可靠性。而且本文BP神经网络采用s型函数，通过归一化能够防止神经元输出饱和现象，使网络快速收敛。因此，首先在MATLAB中对以上7个影响因素进行数据归一化处理到[0，1]区间。

x'=x-xminxmax-xmin                  （14）

3 模型分析与修正结果

BP神经网络为缩短网络训练时间与提高训练精度，通常选择较少的隐含层结点数[7]。本文选取学习率lr=0.000 1，最大训练次数epochs=10 000，收敛误差goal=1e-3，隐含层神经元结点数为9，训练函数为trainlm。训练网络中将输入数据的70%作为训练集，15%作为测试集，15%用来进行模型预测[15]，仿真结果如图2所示。运用BP神经网络对2017-2018年24个月的纯电动汽车销售量进行预测，其实际值与预测值相对误差如表1所示。将相对误差分为6个状态，分别为：E1：-35%～-20%，E2：-20%～-5%，E3：-5%～10%，E4：10%～25%，E5：25%～40%，E6：40%～55%。

根据相对误差划分状态，利用马尔科夫进行优化，由上述的马尔科夫模型可求得一次状态转移概率为：

P1=03/401/92/94/91/30001/20011/6010  01/401/901/9000000000100            （15）

将2018年12月作为初始状态α0=010000，根据马尔科夫原理可求得2019年1月状态为α1=α0？P1=1/92/94/91/901/9，则所处状态为E3，对应相对误差为（-5%+10%）/2=2.5%，Markov-BP神经网络模型预测值为6.35×1+2.5%=6.51。同理，利用Markov-BP神经网络模型可得出2019年2月-9月的纯电动汽车预测值，如表2所示。

从BP神经网络模型与Markov-BP神经网络模型对纯电动汽车销售量预测的相对误差对比可以发现，Markov-BP神经网络模型预测值的相对误差更小，因而提高了预测准确度。

4 结语

在提倡绿色发展的大背景下，政府支持纯电动汽车的研发与推广，但现阶段纯电动汽车的销售情况并不乐观。因此，对纯电动汽车销售量进行准确预测，可以减少资源浪费，降低企业成本。本文选取影响纯电动汽车销售量的7个关键因素，利用BP神经网络模型对现有数据进行训练，用测试好的模型预测2019年1月-9月纯电动汽车销售量，再用马尔科夫（Markov）模型修正其预测值。通过对比发现，Markov-BP神经网络模型的预测精度更高，可有效弥补BP神经网络预测的不足。但本文选取的纯电动汽车销售量影响因素不够全面，未结合纯电动汽车价格及相应技术指标进行综合考虑。因此，充分考虑这些影响因素，并找到更合适的纯电动汽车销售量预测模型，是下一步的研究方向。

参考文献：

[1] 孙婷婷，沈毅，赵亮. 一种基于BP神经网络的房价预测模型[J]. 电脑知识与技术，2019，15（28）：215-218.

[2] 董丽丽，费城，张翔，等. 基于LSTM神经网络的煤矿突水预测[J]. 煤田地质与勘探，2019，47（2）：137-143.

[3] 刘璐，丁福利，孙立民. 基于SVM的烟草销售量预测[J]. 软件导刊，2016，15（11）：134-137.

[4] 张茜，冯民权. 基于BP神经网络马尔科夫模型的漳泽水库水质预测[J]. 黑龙江大学工程学报，2018，9（2）：38-44.

[5] 王保賢，刘毅. 基于灰色BP神经网络模型的人力资源需求预测方法[J]. 统计与决策，2018，34（16）：181-184.

[6] 李军怀，高瞻，王志晓，等. 基于指数平滑和马尔可夫链的短时交通流量预测[J]. 计算机系统应用，2013，22（12）：132-135.

[7] 黄羹墙，杨俊杰. 基于BP神经网络与马尔可夫链的短期电价预测[J]. 上海电力学院学报，2017，33（1）：1-3，10.

[8] 石萍，黎俊辉，刘洪. 新能源电动车销量预测模型的应用[J]. 辽宁科技大学学报，2016，39（5）：395-400.

[9] 周彦福，王红蕾. 我国新能源汽车月度销售量预测模型研究[J]. 软件导刊，2019，18（8）：149-153.

[10] 陈娟，曹沁愉. 基于马尔科夫链对BP神经网络法残差修正模型的短期风电功率预测[J]. 电力与能源，2017，38（5）：567-570.

[11] 王奕翔，陈济颖，王晟全，等. 基于改进型RF-BP神经网络的房地产价格预测[J]. 工业控制计算机，2019，32（10）：122-124.

[12] 陈广银，蔡灏兢，姜欣. 马尔可夫修正的BP神经网络在PM2.5预测中的应用[J]. 能源环境保护，2017，31（5）：8-11.

[13] WANG H，XU L，WANG X. Outage probability performance prediction for mobile cooperative communication networks based on artificial neural network[J]. Sensors，2019，19（21）：4789-4805.

[14] 徐森. 基于BP神经网络的甘肃省公路客运量预测方法[J]. 交通与运输，2019，35（5）：28-31.

[15] 王筱欣，高攀. 基于BP神经网络的重庆市房价验证与预测[J]. 重庆理工大学学报（社会科学），2016，30（9）：49-53.

（责任编辑：黄 健）