基于高阶图卷积自编码器的网络流量预测

崔兆阳　李昭桦

摘   要：网络流量预测是有效保障用户QoS措施之一。当前深度学习为基础的网络算法预测中没有充分利用网络拓扑信息。为此，提出了基于高阶图卷积自编码器的网络流量预测模型。该流量预测模型基于软件定义网络（SDN）架构，利用高阶图卷积网络（GCN）获取网络拓扑中的多跳邻域之间的流量相互影响关系，采用门控递归单元（GRU）获取网络的时间相关性信息，利用自编码模型来实现无监督学习和预测。在Abilene网络上采用真实数据进行了仿真对比分析试验，结果表明，提出的方法在网络流量检测方面的MAPE值为41.56%，低于其它深度学习的方法，同時预测准确率方面也达到最优。

关键词：流量检测;高阶图卷积;GRU自编码器;网络拥塞预测

中图分类号：TP39                                            文献标识码：A

Network Traffic Prediction Based on k-hops

Graph Convolutinal Autoencoder

CUI Zhao-yang1，LI Zhao-hua2

（1. Guangzhou Power Supply Bureau Co.，Ltd.，Guangzhou，Guangdong 510620，China;

2. Guangdong Electric Power Design and Research Institute Co.，Ltd.，China Energy Construction Group，

Guangzhou，Guangdong 510663，China）

Abstract：Network traffic prediction is one of the effective way to improve user QoS. The network topology information is not fully utilized in current network algorithm prediction. A network traffic detection model based on high order graph convolutional network algorithm is proposed，and further predicts network congestion based on traffic information. The traffic prediction model utilizes the graph convolutional to capture the mix-hop effect of traffic. And the gated recurrent unit （GRU） obtains the time correlation information of the traffic in the network. The autoencoder model implements the unsupervised learning and traffic prediction. The simulation experiment is on the real data of the network Abilene. The experimental results show that the mean absolute percentage error（MAPE） value of the method in network traffic detection is 41.56%，which is lower 1.64% than DCRNN methods，at the same time，the prediction accuracy is also optimal.

Key words：network traffic detection;k-hops graph neural network;GRU autoencoder;network traffic prediction

随着5G的发展，电信网络变得越来越复杂，拥有准确及时的流量预测对于大多数网络运营/管理任务至关重要，如网络异常检测、流量计费、短时流量调度或重新路由，长期容量规划，网络设计[1-3]。由于网络流量具有自相似性、多量级、长距离依赖性和高度非线性，这些统计特征决定了网络流量具有可预测性[4]。通常考虑两类基于长期和短期的预测方法，长期流量预测用于估计未来的容量需求，从而实现更有效的规划决策。短期流量预测（即，在几分钟甚至几秒内的预测）通常与动态资源分配相关联，并且可用于改进服务质量（QoS）机制以及拥塞控制和最佳资源管理。

电信网络的拓扑结构是具有图网络结构性质的，路由器和交换机构成网络的节点。电信网络的流量是在节点之间交换并跨越网络链路。通过网络节点的流量与网络节点的相邻链接的节点相互影响，即相邻的节点彼此之间的流量具有相关性。 例如，已经发生拥塞链路的相邻链路中发生拥塞的可能性更大。尽管当前有很多方法在对网络流量进行预测，但是，这些传统机器学习算法并没有考虑电信网络的拓扑结构[1-2]。

为此，提出了基于图网络自编码器的网络流量预测方法。与传统的流量预测相比较，所提出的方法利用图网络获取网络拓扑属性，通过自编码方式来解决网络流量的数据标签标记的问题。在真实数据集上与以CNN为基础的预测方法、LSTM（Long Short Term Memory networks）方法等相比，所提出的方法有明显的优势。

1   相关工作

高带宽和低延迟则是以5G网络发展的需求，因此，准确预测网络流量[1，2，5-7]对于网络运营商来说至关重要，因为它可以实现资源的高效管理和负载平衡。随着深度学习技术的发展，将深度学习算法引入到网络流量主动预测成为一个备受关注的研究方向[2，8-11]。基于主动网络流量预测方法允许提供商根据用户需求来进行网络资源优化和分配，满足用户对网络QoS的要求。

Nie等[2]采用深度学习架构来探索网络流量的动态特性，提出了一种基于链路计数和路由信息统计的深度信念网络流量预测方法。Zhuo等[12]提出了一种基于时间序列自相关系数分析的预测模型，以提高预测的准确性。在考虑模型参数的自相关特征的基础上，实现了长短期记忆（LSTM）与递归神经网络（RNN）相结合的预测算法。Azzouni等[6]提出了一种基于LSTM RNN的网络流量矩阵预测框架。他们利用该框架验证了来自GEANT网络的真实数据框架，显示出非常低的均方误差。

Liu等[13]提出了一种将卷积和循环模块结合起来的端到端深度学习架构，该架构可以从网络流量提取空间和时间信息。Cao等提出[14]了一种门控递归单元（GRU）和卷积神经网络（CNN）的组合，用于数据中心的网络流量预测任务。Lei等[5]提出了利用深度自编码器来对网络流量进行预测。Alawe等[3]中通过递归神经网络（RNN）方法研究了5G网络的前传和回程资源流量估计。

然而上述的这些基于深度学习在网络流量预测中将网络作为欧式空间数据对待，都没有明确考虑网络的拓扑信息。而通信网络属于非规则的拓扑结构，传统的CNN和RNN难以有效地提取网络相关信息[15]。Li等[16]采用提出基于图结构数据网络的扩散卷积递归神经网络来捕获交通网络中的时空相关性，实现对交通流量的预测。Wang等[17]将整个城市道路网络采用图网络进行建模，采用图回归神经网络（GraphRNN，GRNN）来对整个网络信息进行分析，实现对所有路段的交通流量预测，并可对未来的交通流量趋势进行预测。Troia等[18]利用GRU编码器来对网络流量进行预测分析。

网络中的流量分布与网络的拓扑结构密切相关，某一节点的网络拥塞不仅与该节点相关，同时与该节点相连的网络通路都相关。为此，将利用高阶图卷积模型来分析邻域网络通路对网络流量的影响。

2   系统模型

2.1   问题描述

在电信网络流量预测中，采用深度学习的方法来进行预测，即根据网络中的历史流量负荷来预测未来的网络流量负荷。假设网络的交换设备都支持SDN，则SDN控制器可以实时地动态感知网络各个节点的流量负载。

电信骨干网络是网状拓扑结构，其中的路由器和交换机可以认为是网络中的节点，交换设备之间的光纤等物理网络可以认为是拓扑网络中的边。假设节点之间交换的流量根据最短路径进行路由。在时间t时刻，SDN控制器感知的网络各个节点的流量负荷可以表示为矩阵X（t）∈RM×1≥0，其中M是网络的链路数。

网络的流量矩阵序列{X（1），X（2），…，X（k），X（k+1），X（k+2），…}具有时间和空间的相关性，因此可以通过历史的流量矩阵序列来对未来的流量进行预估。传统的机器学习方法如线性回归等，以及RNN、LSTM等深度学习方法可以实现预测。但这些预测方法仅仅考虑了流量矩阵X（t）的时间相关性，而没有考虑流量矩阵所蕴含的空间拓扑逻辑关系。

网络的拓扑信息可以用图（Graph） G来表示，网络节点的邻接矩阵A，经过网络的流量表示为X（t）。则网络拓扑的预测问题可以表示为：

X（t+j）=P（A，X（t-1），X（t-2），…，X（t-i））   （1）

其中，P表示流量预测器，i表示用于预测的历史时间段，j表示未来待预测的时间段。预测问题表示的含义为，未来j时刻的网络流量，可以用过去的i个时间段的流量来进行预测。

网络的流量不仅与当前时刻的流量相关，同时与相邻的节点也相关。即网络流量存在时空相关性，因此，预测器P需要能够同时考虑网络的时空相关性。

2.2   门控递归单元（GRU）网络

递归神经网络（RNN）作为一种特殊的神经网络模型结构，解决了历史信息保存的问题。通过RNN的结构，神经元跟踪过去的信息并用它来影响当前时刻的输出，使其适用于预测时间序列数据。但是，由于RNN存在梯度消失的问题[19]，LSTM是一种特殊的RNN类型被广泛应用到时间序列预测。门控递归单元递归神经网络（GRU RNN）[20]，是LSTM的简化模型，GRU 是新一代的循环神经网络，与 LSTM 非常相似。与 LSTM 相比，GRU 去除掉了细胞状态，使用隐藏状态来进行信息的传递。它只包含两个门：更新门和重置门。其中，更新门的作用类似于 LSTM 中的遗忘门和输入门，它决定了要忘记哪些信息以及哪些新信息需要被添加。重置门作用是决定遗忘先前信息的程度。GRU 的张量运算较少，因此它比 LSTM 的训练更快。

GRU状态更新过程[20]如下：

zt = σ（Wz·[ht-1，xt]）     （2）

rt = σ（Wr·[ht-1，xt]）     （3）

■t = tanh（W·[rt * ht-1，xt]）     （4）

ht = （1 - zt）*ht-1 + zt * ■t     （5）

2.3 高階混合图网络自编码模型（GGRU-AE）

通信网络是一种典型的图结构网络。假设通信网络的节点集合用V表示，图中边的集合用E表示，如果节点Vi和Vj相连则Eij = 1，否则为 。则通信网络的拓扑可以表示为G = （V，E）。假设网络传递的信息表示为X∈RN × P，其中N为网络中节点的个数，P为节点传递的信息的维数。网络节点的邻域权重矩阵A∈RN × N为实对称矩阵，网络节点的度矩阵为对角矩阵，可以表示为Dii = ∑j Aij。网络的图拉普拉斯矩阵定义L = D - A，其正则化表示为Ls = D■LD■。

信息X在通信网络中的传播过程采用LSTM或者CNN的方式较为容易处理。考虑到信息X在网络G中的传递过程与网络的邻域权重矩阵相关，同时信息传递过程为每个节点对所有其他节点的影响提供了重要的线索。在扩散卷积递归神经网络中[16]，只考虑了一阶形式来定义信息传递的过程，这将与实际的情况有差距，因此，在研究中采用高阶形式来定义信息传播过程。信号X∈RN × P在图网络中的传递过程为信息X与图滤波器fθ卷积过程，定义如下：

X*g fθ = ■（θk，1（D■AD■）k +

θk，2（D■AD■）k）·X     （6）

其中，*g表示图卷积，θ∈Rk×3是滤波器的参数，D■AD■是扩散过程的状态转移矩阵，参数C为常数，不同的C表示邻域的阶数。

假设■ = D■AD■，则（D■AD■）k = ■k。当c=2时，按照文献[21]的方法将式（6）展开形式为：

X*g fθ = （θ1，1 ■ + θ1，2 ■）·X+（θ2，1 ■2 + θ2，2 ■2）·X

= ■XW1 + ■2XW2       （7）

其中，W1 = θ1，1  + θ1，2 ，W2 = θ2，1  + θ2，2。如果選择的阶数c越大，对于大尺度的图网络中，直接计算■k将是消耗大量的计算资源，■kXWk = ■（■k-1XWk）的迭代方式降低计算复杂度。

信息的传递卷积算子采用基于GRU的传递卷积层来构建，可实现将信号矩阵X∈RN×P映射到传播输出矩阵H∈RN×Q：

H：，q = σ（■X：，q* fθq，p，：，：），？坌q∈{1，…，Q}    （8）

其中，θ∈RQ×P×K×3为可训练权重参数的高阶张量表示形式。

与经典的GRU状态更新过程（2）～（5）相似，采用高阶扩散图卷积的信息传递GRU的结构也与图1相同，只是相关的参数变为张量。张量GRU的状态更新[16]实现过程定义如下：

r（t） = σ（θr*g [H（t-1），X（t）] + br）    （9）

■（t） = tanh（θt*g [（r（t）⊙H（t-1）），X（t）]+bt）

（10）

Z（t） = σ（θz*g [H（t-1），X（t）] + bz）    （11）

H（t）=Z（t）⊙■（t）+（1-Z（t））⊙H（t-1） （12）

其中，r（t）为复位门的输出，■（t）为GRU状态，

Z（t）为更新门的输出，⊙为张量乘法。待训练的参数为θr，θt和θz及对应的偏置br，bt和bz。训练过程采用梯度下降法。

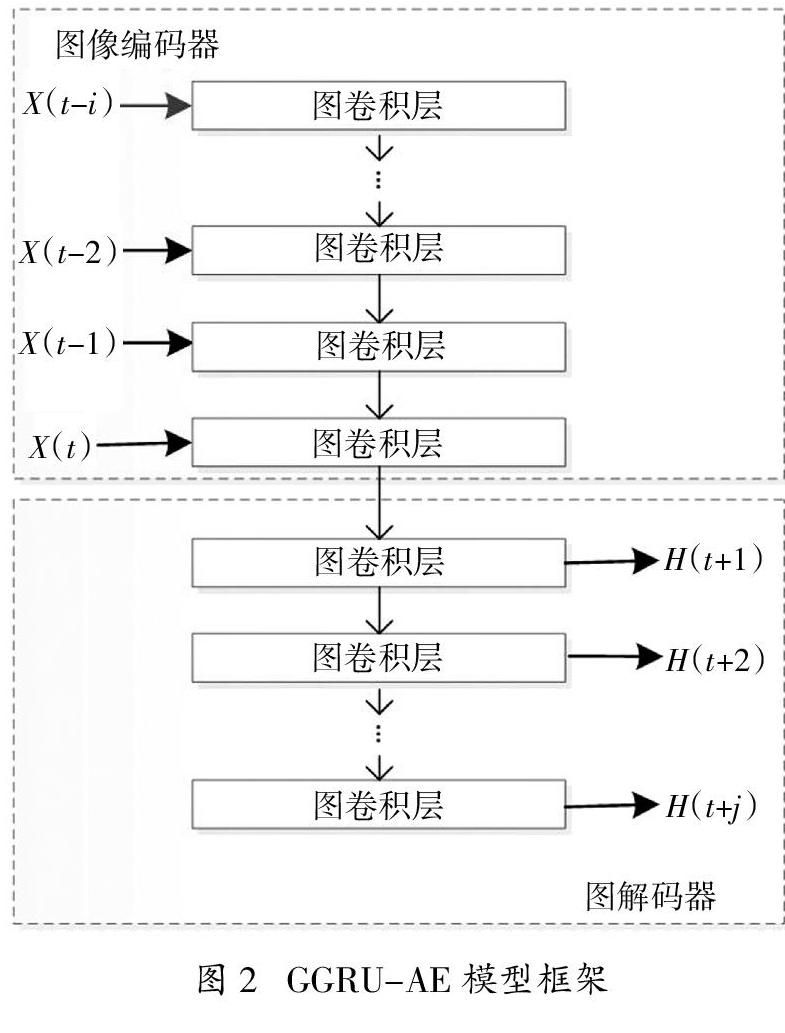
在GRU和高阶GCN的基础上，提出的GGRU-AE模型框架如图2所示。模型以高阶图卷积层为基本单元，包括编码器和解码器。模型的输入为图网络的流量矩阵虚拟{X（t-i）}，输出值为预测值H（t + j）。

模型的训练阶段包括预训练和微调两阶段。在预训练中，采用逐层贪婪（Greedy Layer-Wise）无监督学习算法来训练网络模型。在参数微调阶段采用基于梯度的优化技术反向传播算法进行模型参数微调。

3   实验及结果分析

3.1   数据集

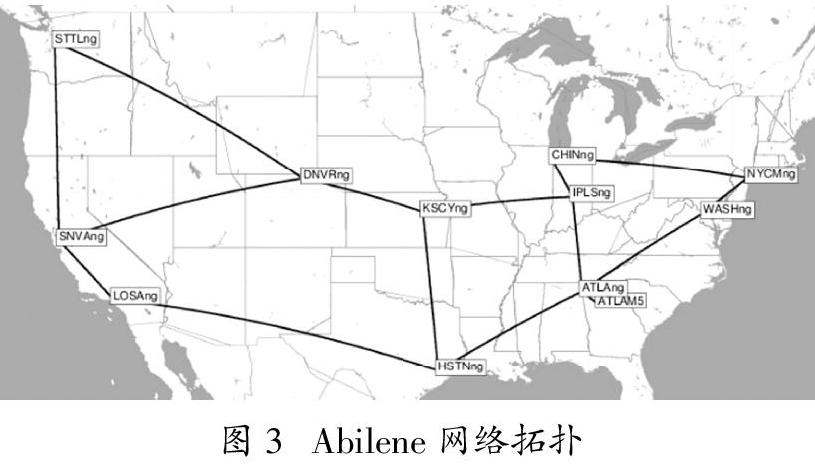
为了评估提出GGRU-AE模型，采用公开的真实数据集Abilene网络来进行评估。Abilene网络的拓扑结构如图3所示，该网络的包含12个交换节点和30条节点之间的物理链路（可以认为是12个节点，15条边的有向图）。因此，可以根据这些公开信息构建出网络的邻接矩阵及其图拉普拉斯矩阵。

从Abilene网络的拓扑结构信息，可以获得了一个12×12的邻接矩阵，表示其节点与网络链路唯一关联的图形。为了方便后续的流量预测，对邻接矩阵中实际存在的节点连接进行编码。即图网络可以构建为矩阵形式，该矩阵为稀疏矩阵，其中的30个值为非零，其余的值为0。非零的值代表Abilene网络中的物理相链接。

在真实数据集Abilene网络公开了网络节点的流量数据，本文选择2004年3月1日到2004年9月10日期间的网络节点的5分钟间隙的公开数据流量作为测试验证数据集。采用文献[1]的方法对数据进行预处理。

假设Abilene网络中任意两个节点之间的路由采用最短路径路由算法Dijkstra。根据公开的流量数据信息及网络拓扑信息，可以计算获得以1个小时为时间度量单位的网络流量聚合信息，这些信息反映每条链路每个小时的流量信息。将每一个小时构建为输入矢量X（t） = {x1（t），…，x30（t）}。将这些流量信息按照时间先后顺序进行排列构成向量序列{X（t），1≤t≤4 000}。为了有效的进行模型训练和预测，将流量数据集中的70%的向量用于模型参数的训练，将其中的20%用于验证训练参数，其中的10%的数据用于测试验证。

3.2   评估方法

为了评价本文的基于图编码器的模型的性能指标。 使用三个性能指标：均方根误差（RMSE），平均绝对误差（MAE）和平均绝对百分比误差（MAPE）。 这些指标的具体计算公式如下：

RMSE = ■    （13）

MAE = ■■Ik - Pk       （14）

MAPE = ■■■       （15）

其中Ik表示在k时刻时网络中所观察的流量数量，Pk是k时刻时网络中流量的预测值，N表示评估样本的总数。RMSE测量极值效应和预测值的误差范围，MAE测量平均预测值的特异性。它们都评估绝对误差。MAPE反映了相对误差。当MAPE最小化时，将该模型视为最佳模型。

3.3 试验基准

为了和所提出的模型进行对比，选择了典型的深度学习预测算法，包括基于LSTM的网络，基于CNN的网络，基于CNN-LSTM的网络和完全连接的神经网络（FC）。基于LSTM的网络由5个循环层组成，每个层包含20个LSTM单元。基于CNN的网络由1层组成，使用32个大小为2的内核实现卷积。基于CNN-LSTM的网络由1个复合层20个LSTM单元堆叠在CNN层之上（16个内核尺寸为2）。全连接神经网络由3层30，20和10个单元组成，对其输入应用Sigmoid函数作用于输入。

所提出的GGRU-AE模型参数中，设置学习率为0.005，采用早期停止来中断训练，训练轮数为100轮。

3.4   实验结果

实验结果以训练100次所得到的平均结果作为模型的实验结果的输出。本模型中考虑不同阶数的邻域，构成了两种类型的模型。模型GGRU-AE-1表示采用的鄰域为1阶邻域，即公式（6）中C = 1。模型GGRU-AE-2表示采用2阶邻域，即在公式（6）中C = 2。

GGRU-AE模型的试验对比结果如表1所示，其中对比测试方法的基准值源于文献[1]。从实验结果的各项对比指标来看，提出的考虑高阶邻域的网络预测模型取得了最好的结果。从结果上来看，以图网络模型为基础的方法，包括两种模型和DRCNN模型比传统的深度学习模型有显著的优势。

在MAE指标上，GGRU-AE-2和GGRU-AE-1比一阶图扩散模型DCRNN分别提高约5.2Mbit/s和2.8Mbit/s。在RMSE指标上，GGRU-AE-2和GGRU-AE-1比一阶图扩散模型DCRNN分别提高约25.7Mbit/s和14.5Mbit/s。在MAPE指标中，GGRU-AE-2和GGRU-AE-1比一阶图扩散模型DCRNN下降了1.64%和0.27%。

将GGRU-AE预测模型用于对网络拥塞进行预测。在Abilene网络中，假设流量负荷网络高于网络中流量负荷的平均值，则认为是出现网络拥塞。假设参数β为高出平局负荷水平的倍数。通过对网络中原始数据的进行统计分析，可以得到任意时刻网络中的平均流量负荷及任意一个网络节点的流量负荷。因此，可以得到相应的真值的标签。预测结果如图4所示，水平轴表示负荷倍数，纵轴表示预测准确率。从图中来看，随着负荷量增加，各个模型的预测准确率均上升。本文的2阶方法GGRU-AE-2在所有的负荷量下均取得最优。

4   结   论

利用高阶图卷积网络自编码器对网络流量进行了检测，并在检测的基础上进行了流量拥塞的预测。高阶图卷积GRU自编码模型，通过图卷积获得网络的空间信息，通过GRU获得时间序列信息。仿真结果表明提出的GGRU-AE一阶网络和二阶网络无论是在流量检测和拥塞预测方面的都较基准方法更优。

参考文献

[1]    ANDREOLETTI D，TROIA S，MUSUMECI F，et al. Network traffic prediction based on diffusion convolutional recurrent neural networks[C]. IEEE INFOCOM 2019 - IEEE Conference on Computer Communications Workshops （INFOCOM WKSHPS），Paris，France，2019：246-251.

[2]    NIE L，JIANG D，GUO L，et al. Traffic matrix prediction and estimation based on deep learning in large-scale IP backbone networks[J].  Journal of Network and Computer Applications，2016， 76：16-22.

[3]    ALAWE I，HADJADJ-AOUL Y，KSENTINI A，et al. Smart scaling of the 5G core network：an RNN-based approach[C].2018 IEEE Global Communications Conference （GLOBECOM），Abu Dhabi，United Arab Emirates，2018：1-6.

[4]    BABIARZ R，BEDO J S. Internet traffic mid-term forecasting：a pragmatic approach using statistical analysis tools[C]. International Conference on Research in Networking. 2006：Springer， Berlin Heidelberg，2006：110-122.

[5]    LEI F，DAI Q，CAI J，et al. A proactive caching strategy based on deep learning in EPC of 5G[C].  International Conference on Brain Inspired Cognitive Systems. 2018：Springer，Berlin Heidelberg 2018：738-747.

[6]    AZZOUNI A，PUJOLLE G. NeuTM：a neural network-based framework for traffic matrix prediction in SDN[C].  NOMS 2018 - 2018 IEEE/IFIP Network Operations and Management Symposium，Taipei，2018：1-5.

[7]    SHUKLA S，BHARDWAJ O，ABOUZEID AA，et al. Proactive retention-aware caching with multi-path routing for wireless edge networks[J]. IEEE Journal on Selected Areas in Communications，2018. 36（6）：1286-1299.

[8]    郭馮宁，宋超，朱琪超，等. 面向交通流量预测的多组件时空图卷积网络[J].  软件学报，2019，30（03）：759-769.

[9]    袁魏彬. 相空间重构和极限学习机的网络流量预测模型[J].  控制工程，2018，25（11）：2087-2091.

[10]  余郭佳，杨晨阳. 基于全注意力机制的多步网络流量预测[J].  信号处理，2019，35（05）：758-767.

[11]  LEI F，CAI J，DAI Q，et al. Deep learning based proactive caching for effective WSN-enabled vision applications[J].  Complexity， 2019，2019：1-12.

[12]  ZHUO Q，LI Q，YAN H，et al. Long short-term memory neural network for network traffic prediction[C]. 2017 12th International Conference on Intelligent Systems and Knowledge Engineering （ISKE），Nanjing，2017：1-6.

[13]  LIU Y，ZHENG H，FENG X，et al. Short-term traffic flow prediction with Conv-LSTM[C].2017 9th International Conference on Wireless Communications and Signal Processing （WCSP），Nanjing，2017：1-6.

[14]  CAO X，ZHONG Y，ZHOU Y，et al. Interactive temporal recurrent convolution network for traffic prediction in data centers[J].  IEEE Access，2017，6：5276-5289.

[15]  BRONSTEIN M M，BRUNA J，LECUN Y，et al. Geometric deep learning：going beyond euclidean data[J].  IEEE Signal Processing Magazine，2017，34（4）：18-42.

[16]  LI Y，YU R，SHAHABI C，et al. Diffusion convolutional recurrent neural network：Data-driven traffic forecasting[J].  arXiv preprint arXiv：170701926，2017.

[17]  WANG X，CHEN C，MIN Y，et al. Efficient metropolitan traffic prediction based on graph recurrent neural network[J].  arXiv preprint arXiv：181100740，2018.

[18]  TROIA S，ALVIZU R，ZHOU Y，et al. Deep Learning-based Traffic Prediction for Network Optimization[C]. 2018 20th International Conference on Transparent Optical Networks （ICTON），Bucharest，2018：1-4.

[19]  BENGIO Y，SIMARD P，FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J].  IEEE transactions on neural networks，1994，5（2）：157-166.

[20]  CHO K，VAN MERRI？NBOER B，BAHDANAU D，et al. On the properties of neural machine translation：Encoder-decoder approaches[J].  arXiv preprint arXiv：14091259，2014.

[21] KIPF TN，WELLING M. Semi-supervised classification with graph convolutional networks[J].  arXiv preprint arXiv：160902907， 2016.