RBF神经网络的境外旅游人数预测模型研究

宫园园　艾宏志

摘   要：針对传统的境外旅游人数预测模型预测误差大的情况，设计了基于RBF神经网络的境外旅游人数预测模型。首先对旅游样本数据进行归一化处理，对境外旅游人数变动统计。然后通过预测种群构建、评估适应值、惩罚项设置、预测序列平稳性检验、模型预测五个过程完成了基于RBF神经网络的境外旅游人数预测模型的设计。最后，实验证明，RBF神经网络的境外旅游人数预测模型比传统的境外旅游人数预测模型误差小，能够准确对境外旅游人数预测。

关键词：RBF神经网络;旅游;人数;预测;节点;误差

中图分类号：TP183                                      文献标识码：A

Study on Prediction Model of Overseas Tourists

Based on RBF Neural Network

GONG Yuan-yuan ，AI Hong-zhi

（Yulin University，Yulin，Shaanxi 719000，China）

Abstract：in view of the large prediction error of the traditional prediction model of the number of overseas tourists，a RBF neural network prediction model of the number of overseas tourists is designed. Firstly，the tourism sample data is normalized，and the number of overseas tourists is counted. Then，the prediction model of overseas tourists based on RBF neural network is designed through five processes：prediction population construction，evaluation of fitness value，penalty item setting，prediction sequence stability test and model prediction. Finally，experiments show that the RBF neural network model designed in this paper has less error than the traditional model，and can accurately predict the number of overseas tourists.

Key words：RBF neural network;tourism;population;prediction;node;error

改革开放以来，旅游业作为第三产业迅速发展，近年来，由于游客拥挤、超载等问题造成的安全问题事故频发，给旅游景区造成很大的负面影响，因此科学准确的对境外旅游人数预测是目前亟需解决的问题[1-2]。

旅游预测对国家制定旅游发展政策和战略规划、优化旅游市场资源配置、旅游企业制定战略计划和决策等方面具有重要作用[3]。境外旅游人数的分析和预测是旅游规划与管理的关键性、基础性工作，但是境外旅游人数预测会受到自然气候、休假制度、突发事件等多种外部因素影响，游客流量表现出非线性、季节性、随机性等复杂特点，导致传统的预测方法预测误差较大。RBF（Radial Basis Function）神经网络是神经网络的一种，RBF为径向基函数，即某种沿径向对称的标量函数，能够优化神经网络的非线性拟合能力，使神经网络可映射任意复杂的非线性关系，并且便于计算机实现，适用于解决分类问题[4]。

为了提高境外旅游人数预测精度，设计了RBF神经网络的境外旅游人数预测模型，该模型以历史数据作为研究基础，对境外人数进行预测，观察其变化规律。首先对境外旅游人数变动统计分析，然后构造基于RBF神经网络的结构形式，通过预测种群构建、评估适应值、惩罚项设置、预测序列平稳性检验、模型预测实现了境外旅游人数预测。实验结果表明，境外旅游人数预测模型比传统预测模型误差小，能够准确对境外旅游人数预测，为旅游管理者提前决策提供直接信息。

1   RBF神经网络的境外旅游人数预测模型

1.1   境外旅游人数变动统计

境外旅游人数预测会受到多种因素影响，为减少境外旅游人数预测[5]的误差，对境外旅游人数变动情况进行统计分析。由于对境外旅游人数预测，需要对历史的境外旅游人数分析，因此，对历史的旅游样本数据进行归一化处理[6]，处理流程如图1所示。

由于RBF神经网络输入的数据范围一般在[0，1]，归一化处理公式为：

A = ■    （1）

式中，Amax取最大值，保证预测年的数据小于该数值，Amin取小于样本数据序列中的最小值，保证归一化处理后的样本数据不接近于0。

由于境外人口数量波动[7]较大，规律不明显，因此采用延时坐标法进行相空间重构[8]，假设一维时间序列为Y = （y1，y2，…，yn），截取其前i个数据构成i维相空间的一个向量，然后依次向后移χ个向量，构成 维空间的第n个向量：

y = （y1+（r-1），y2+（r-1），…，yn+（r-1））    （2）

通過上述序列得到i向量的点集，根据该点集，对境外旅游人数变动统计分析。根据境外旅游者人数在一定时期所增长的绝对数量，统计旅游者人数增长量[9]，增长量可以为正数，也可以为负数。境外旅游人数的旅游人数增长量用公式表达为：

DT = a1 - a2 - a3 - … am      （3）

式中，a1、a2、a3和am分别代表各个时期的旅游者人数，其中a1为初始者人数，am为最末期的旅游者人数，其余为中间各个旅游时期的旅游人数。

在此基础上，对逐期增长量计算，其为各报告期旅游者人数与当前旅游者人数之差[10]，用公式表达为

Rgb（a） = a1 - a0，a2 - a1，… an - an-1     （4）

式中，a1 - a0、a2 - a1、an - an-1分别代表同一时期的增长量。

通过上述步骤，完成对境外旅游人数变动的统计分析，为境外旅游人数预测提供一定基础。

1.2   境外旅游人数预测模型构建

依据上述对境外旅游人数变动的统计分析，以RBF神经网络为基础，构建境外旅游人数预测模型，构建模型的过程如下：

步骤一：根据相关专家学者的研究成果，选择适用于构建RBF神经网络的结构。全部的非线性函数关系的任一精度均可以被仅含有一个隐含层的神经网络逼近，也可称为三层前馈神经网络。故此次构建的境外旅游人数预测模型选用三层前馈型神经网络，并以此次构建模型所选择的6个指标数量作为神经元个数。根据前人研究资料可知，目前较难判断隐含神经元数量，且判断方法并不确定，但隐含层节点数需满足2n > t（t为输入层节点个数）。根据满足条件，此次构建模型中隐含层含有3个神经元，输入层含有2个神经元，输出层含有1个神经元，其中输出层的神经元即城乡居民消费能力的综合值。

步骤二：将RBF神经网络的参数进行初始化设置。将较小随机数给予网络隐含层、输入层与输出层，其连接权值为ω、ω′，阈值为θ、θ′。

步骤三：根据RBF神经网络的输入量数值，获取最佳评估指标。

步骤四：计算隐含层神经元的输入x′、输出y′与输出层神经元的输入x″、输出y″。

步骤五：神经元误差u表达式为：

u = ω（t - y″）′ω′（x″）       （5）

步骤六：RBF神经网络机构计算公式为：

Fx = ■{uω′}■t（x″） = W1 + W2 + … + Wn   （6）

步骤七：权值及阈值的矫正过程为：

ω（u + 1） = ω（u） + Δω（u）     （7）

ω′（u + 1） = ω′（u） + Δω′（u）      （8）

θ（u + 1） = θ（u） + Δθ（u）      （9）

θ′（u + 1） = θ′（u） + Δθ′（u）      （10）

步骤八：为达到理想精度，减小总误差，选择下一列模式作为输入信号，并将全部训练模式运行一周。

把未满足理想精度的训练模式返回并重新训练，获取最佳的城乡居民消费能力评估结果。

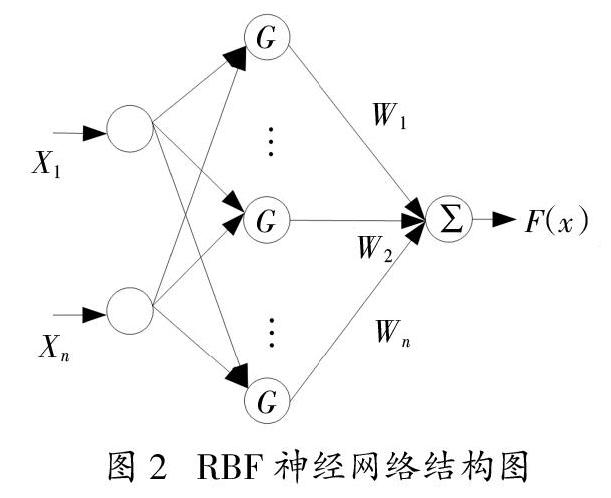
RBF神经网络结构图如下所示：

在此基础上，运用RBF神经网络进行预测，预测流程如图3所示。

1.2.1   构造基于RBF神经网络的结构形式，将该模型中的输入节点数值设置大于该序列嵌入维数[11-12]。经过反复实验将网络层节点数最终确定为4个，输出层节点数为1，隐含层节点数量为6个;

1.2.2   预测种群构建，利用染色体表示问题的潜在解，形成初始种群，并根据目标函数确定适应度函数，根据适应度函数值[13]的大小，对选择的个体进行交叉和变异等遗传操作，保留适应值好的个体，以此反复循环，构建种群预测。

1.2.3   评估适应值，训练初始化后的境外旅游人数参数，为避免训练集的适应值陷入过度拟合状态[14]，选用CB方法，计算公式为：

DV = ■     （11）

式中，y和■分别为境外旅游人数的预测值和实际值，■a代表训练样本数目，■代表径向基适应值函数。

1.2.4   惩罚项设置[15]，在通过多次训练比较后，为适应外界输入，加入惩罚项，以提高预测模型的综合性能，计算公式如下：

D = ■？圯Wa         （12）

式中，D为非线性惩罚项参数，■代表旅游人数预测参数，Wa代表旅游人数预测影响参数。

通过上述公式，对惩罚项设置，减少境外旅游人数预测误差。

1.2.5   预测序列平稳性检验，通过时间序列的散点图对旅游人数序列进行初步的平稳性判断，计算公式如下：

gh = ■q*ik          （13）

式中，gh代表旅游数据序列，■q代表时间序列，ik代表历史旅游人数。

根据上述公式，检测预测序列，目的是检验预测模型对原时间序列的拟合效果，检验整个模型中信息提取是否充分。

根据模型参数检验结果，确定最终的境外旅游人数预测模型。根据上述定义，完成基于RBF神经网络的境外旅游人数模型的建立，并为验证此次模型设计的有效性，将在下一步进行实验。

2   仿真实验

2.1   实验准备

为验证基于RBF神经网络的境外旅游人数预测模型的有效性，进行实验验证。并为了使实验结果更具说明性，将传统的预测模型与本预测模型作对比，主要对比两种模型的预测误差。此次实验样本来自于我国某地的旅游风景区，选取该景区的2009年国庆节时7天数据，分别使用两种模型对这7天的境外旅游人数进行预测。为使实验结果更加直观，建立误差评价指标，分别计算传统预测模型和本预测模型的误差值，误差值最佳理想值为0，其值越低，代表实际值和预测值越接近，则代表误差小。误差评价指标的计算公式如下：

MAPE = ■■vd？圯b          （14）

式中，为实际境外旅游人数，代表境外旅游人数预测值，反应实际值与预测值之间的偏差，为实际值与预测值的相关程度，为测试样本数量。

2.2   实验结果分析

实验天数选取国庆的7天假期，该景区的实际每天境外旅游人数为已知，为使实验结果更加直观，只对比两种预测模型的误差值，实验对比结果如下所示：

分析上述实验结果可知，在第1天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高4.7;在第2天的旅游人数预测上，传统预测模型的预测误差值比本模型的预测误差值高5.4;在第3天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高7.4;在第4天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高8;在第5天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高9.76;在第6天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高4.12;在第7天的旅游人数预测上，传统预测模型的预测误差值比本预测模型的预测误差值高7.02。

分析總体实验结果可知，本预测模型的整体预测误差都比传统预测模型的预测误差低，与最佳理想值接近。因此基于RBF神经网络的境外旅游人数预测模型，能够有效对历史数据统计与分类，从而具有较高的预测准确性，因此证明了本预测模型的有效性。

3   结   论

针对传统的境外旅游人数预测模型预测误差大的情况，设计了一种基于RBF神经网络的境外旅游人数预测模型。首先对境外旅游人数变动统计，然后构造基于RBF神经网络的结构形式，最后通过预测种群构建、评估适应值、惩罚项设置、预测序列平稳性检验、模型预测五个过程实现了对境外旅游人数的预测。实验对比结果表明，RBF神经网络的境外旅游人数预测模型比传统的境外旅游人数预测模型预测误差小，能够为旅游决策提供重要支持。

参考文献

[1]    陈美璘，何清龙. 基于熵权法混合模型的贵州省旅游人数预测研究[J].  数学的实践与认识，2018，48（21）：307-313.

[2]    李瑶，曹菡，马晶. 基于改进的灰色模型的旅游需求预测研究[J].  计算机科学，2018，45（1）：122-127.

[3]    胡晓琴. 基于支持向量机的旅游需求量预测模型[J].  现代电子技术，2017，40（15）：105-107.

[4]    段莉琼，宫辉力，刘少俊，等. 基于客源地的聚类-ARIMA模型的短期旅游需求预测——以天津欢乐谷主题公园为例[J].  地域研究与开发，2017，36（3）：108-112.

[5]    党婷，彭乃驰. 基于GM-ES-GASVR组合模型的丽江国内旅游需求预测[J].  数学的实践与认识，2017，47（8）：279-287.

[6]    陈荣，梁昌勇，陆文星，等. 面向旅游突发事件的客流量混合预测方法研究[J].  中国管理科学，2017，25（5）：167-174.

[7]    王晓宇，苏放. 基于BA-SVR的乡村游短期客流预测模型[J].  计算机工程与设计，2018，39（12）：219-223.

[8]    刘静，刘耀龙，段锦. 基于5A景区最大承载量和游客接待量的旅游供需关系模型研究[J].  科技通报，2017，33（7）：264-268.

[9]    张斌儒，郑宗剑，张瑞，等. 基于RVM模型的国内游客流量预测研究——以海南为例[J].  数学的实践与认识，2017，47（24）：30-36.

[10]  魏鹏，侯杨方. 旅游者空间分布模型及其预测应用——以甘肃省县（区）为例[J].  旅游学刊，2017，32（5）：106-115.

[11]  汪威. 最优组合预测线性模型在旅游需求预测中的应用——以中国大陆赴澳门游客量预测为例[J].  数学的实践与认识，2018，48（12）：49-58.

[12]  王玮琳，张海龙. 旅游景区安全事故灰色预测及关联度分析[J].  安全与环境学报，2018，18（6）：2115-2119.

[13]  郭旭东，刘永平，王远回. 以旅游功能为主的城市轨道交通线路客流预测方法[J].  城市轨道交通研究，2018，21（1）：49-52.

[14]  张圆刚，余向洋，程静静，等. 基于TPB和TSR模型构建的乡村旅游者行为意向研究[J].  地理研究，2017，36（9）：1725-1741.

[15]  程丽萍，李仁杰，傅学庆，等. 旅游景观感知度计算模型设计与实现[J].  地理与地理信息科学，2017，33（3）：59-65.