基于陀螺定向的矿井导线测量方法分析

李雁鹏

【摘 要】 矿井巷道正在向大型化超大型化发展，但巷道贯通本身所允许的误差并没有得到相应的减小。本文通过对矿区巷道传统的导线测量方法的分析，详细地分析了水平角的误差直方图，给出了导线测量方法下避免仪器以及人工因素带来的试验粗差方法，同时，对陀螺定向的导向测量方法下误差的分析进行了公式推导，得到该测量方法下误差的计算公式，对于后期数据的处理进行讨论，为矿区进行巷道的测量以及数据的处理提供了参考。

【关键词】 煤矿巷道;导线测量;粗差;陀螺定向

矿区巷道的测量可以实时了解巷道的变形情况，对于煤矿地质灾害的发生有一定的预防作用。本文通过对导线测量方法下误差进行了公式推导，从而定量地对数据进行了处理。

1导线测量方法分析

目前，导线测量方法是矿区用于土地测量最普遍的测试手段之一，导线测量是通过在地面设置一系列的点，这些点连接成不规则的折线，利用测点之前的距離以及角度确定测量区域面积的测量方法。导线测量的基点的选择至关重要，不同基点下不同位置的高度不同，对于后期数据的处理的难易也不同，在测量中，测点的基点应该与矿区坐标保持一致，这是导线测量方法坐标选择的原则。在实际测量的过程中，大多数矿井采用与本矿井的坐标一致的原则进行测量，部分矿井根据国家坐标系进行测量的工作，不论以何种原则选择坐标系，矿区应该以本区域的情况选择适用于测量的坐标系。

从图中可以看出，测试点共有A、B、1、2、3、4六个，每两个相邻的测试点之间都存在一个角度，且相邻测试点之间的距离是已知的。在测量的过程中，如果出现粗差，测量结果就失去了真实性、准确性，测量粗差即观测到的数值和真实数值误差较大的情况，对于测量是否出现粗差，检验方法较为简单，工作人员可以在相同的测点进行多次独立的测量，每次测量时都应该测两个回合，在多次测量后，对比测量之间夹角的差值、测距的差值以及两测差值和多次测量的互差等数据的对比，从而得到准确的位置信息以及角度信息。

在井下进行测量时，带来误差的原因往往是多样的，主要有以下几个方面：

仪器误差。仪器的误差主要是仪器本身的精度并不准确，在加工的过程中，并不能完全保证仪器的精度与设定值一样，而在测量的过程中，三轴误差也会对测量带来很大的影响，视准轴应该通过仪器的盘左、盘右的调整消除，横轴误差与视准轴误差一样可以通过盘左、盘右调整，对于竖轴误差，应该通过改正竖轴倾斜的方法减小误差。

人工误差。人工误差一直伴随着测量的始终，在初期仪器的定位上，应该在合适的坐标系中使得仪器平稳地放置，通过矫正三轴线后，进行仪器的对中工作，减小中心线与巷道顶板铅垂线之间水平角的误差，调整好仪器后，进行测量工作，在测量时，工作人员应该严格地按照读数规定读数，避免因为读数引起的误差。

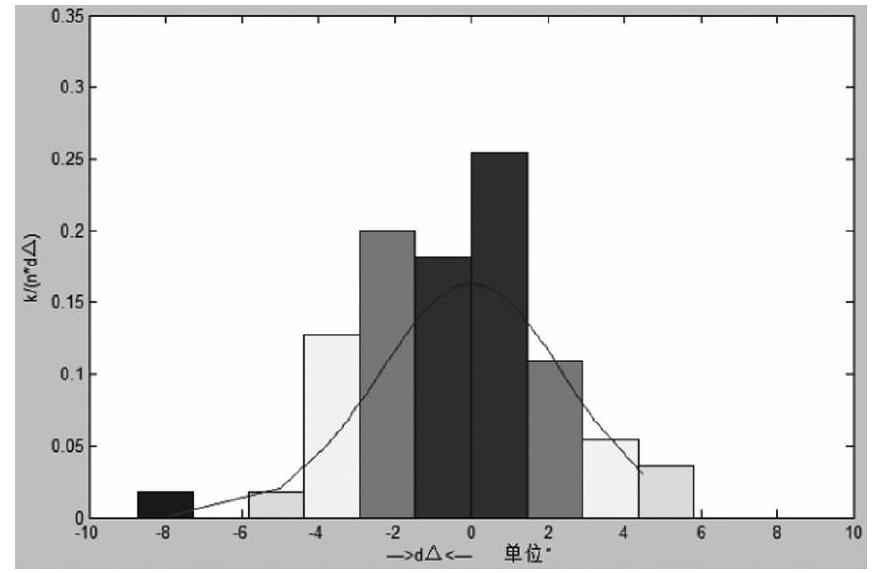
在井下的测量中，因为对于每一个测点的距离、角度等都有一定的精度要求，在众多测点工作中，因为误差的原因，最后也很难达到预期要求的精度，这里，我们研究水平角的误差分析，如图2所示。

从图2可以看出，误差呈现近正态分布的现象，坐标轴横坐标表示误差的正负，纵坐标为误差的大小，从图中可以看出，误差值主要集中于-4到4的区间内，在多段巷道的测量时，最后测量的数据偏差就会不断累积增大，所以对于水平角的观测，应该在测量时正确的放置测量仪器，在仪器平稳的基础上进行对中矫正工作，在井下巷道的测量时，对某区段内的巷道应该进行多次测量避免粗差的影响，同时，应该提高测量工作人员的专业性，在测量时以端正的态度进行规范性的测量以及读数，才能保证测量的准确性，为后续矿井工作的布置提供便利。

2陀螺定向的导向测量方法

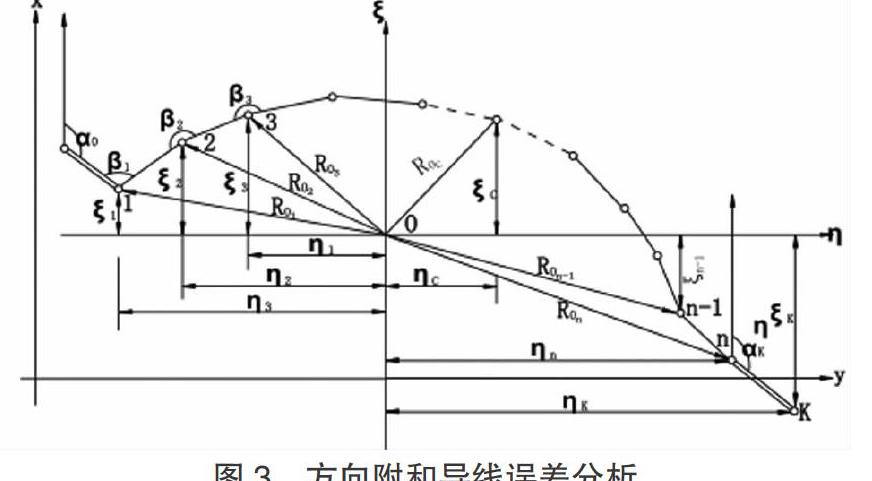
随着测量方法的改进，导线测量方法也有了突破，在巷道掘进初期，因为地势起伏以及地层走向的不同，对于巷道的测量有一定的难度，利用陀螺定向的导线测量方法可以更精确地测量边长以及测点间的方位角，但是因为陀螺经纬仪仪器本身的原因，需要根据测量的条件进行误差的分析，如图3所示。

如图3所示为方向附和导线的误差分析，其中只有测点1的坐标为已知的，之后测点的位置为未知的，其中，ξ为测点到坐标中心的水平距离，η为测点到坐标中心的垂直距离，R为测点到坐标中心的距离，β为测量点的角度值，根据起始测点的位置已知，我们计算得到终点K处的误差公式：

因为测量误差的无法避免性，随着测量的推进，测量的误差会越来越大，所以我们选择了点K进行了误差的分析，其他点的误差也可以参考此点。

测量工作完成后，再对已有的数据进行误差分析是首要的步骤，对于数据的处理是关键，只有把测得的导线数据完整地分析出来，才可以得到矿井巷道的相关尺寸信息，对于传统的导线测量方法，其分析较为简单，对多次测量的结果进行分析对比求差值，并对需要投影的线段进行投影计算，最后统计得到测量数据，相比传统的导线测量方法，外加陀螺定向边的导线测量数据的处理方法就较为复杂，在已有数据的基础上，需要利用赫尔默特进行数据的方差计算，通过不断的迭代运算获得适合于矿井的导向网，然后通过对测点的角度、距离结合陀螺本身的测量特点对数据进行分析处理，得到最后的矿区巷道测量数据。在实际的工程中，每一个矿井的地质条件以及测量坐标系的选择都有所不同，处于对测量精度的要求，每一处的测量都至少进行两次，对于复杂地形，测量的次数以及数据都会增加，对于数据的后期处理也会更加复杂，所以对于实际测量工作，应该选择合适的测量模型以及测量方法进行测量工作。

综合上述的分析，传统的导线测量方法在不断的改进，在不断改进的过程中，对于测量误差的分析是至关重要的，本文对陀螺定向的导向测量方法下误差的分析进行了公式推导，得到可参考的误差公式，同时，对于数据的后期处理进行了分析讨论，在具体的煤矿巷道测量中，应该根据本矿井的地势情况选择合适的坐标系以及测量方法，并进行误差的分析讨论，利用适合的数据处理方法处理数据，可以极大地减小误差，直接利用测量结果。

3结论

文章分析了井下进行测量时，带来误差的原因，主要是仪器误差和人工误差。

基于导线测量的误差分析，建立了陀螺定向导线测量方法的终点误差计算公式。

对于实际测量工作，选择合适的测量模型以及测量方法进行测量工作，可以极大地减小误差，直接利用测量结果。

【参考文献】

[1]饶德庆，李金平，刘长星.矿区独立坐标系的建立及同国家坐标系的转换[J].科技信息，2010（23）：219-220.

[2]邓军，王胜利.加测陀螺定向边的井下导线平差方法探讨[J].资源环境与工程，2006，20（2）：163-167.

[3]韩群柱，耿宏锁，李宇.地下工程导线测量中加测陀螺方位角的最佳位置研究[J].西北农林科技大学学报，2004，32（12）：116-120.

[4]喻小东，张鹏飞.矿井加测陀螺边方向附合导线的数据处理[J].现代矿业，2011（6）：65-66.

[5]笪建原，汪应宏，李钢.复测支导线与闭合导线间的关系探讨[J].矿山测量，2005（1）：46-48.

[6]韩群柱，屈漫利.地下工程直仲支导线陀螺定向精度分析研究[J].西安工业学院学报，2006，26（3）：276-279.

[7]潘国荣，王穗辉.地下导线加测陀螺边最优位置确定及精度分析[J].同济大学学报（自然科学版），2004，32（5）：656-659.

[8]谢峰震.加测陀螺边后巷道贯通最佳点及误差探讨[J].科技创新导报，2008（34）：146-146.