基于改进粒子滤波算法实现锂离子电池RUL预测*

韦海燕，安晶晶，陈 静，王惠民，潘海鸿，2，陈 琳，2

（1.广西大学机械工程学院，南宁 530004；2.广西电化学能源材料重点实验室，广西大学可再生能源材料协同创新中心，南宁 530004）

前言

锂离子电池作为电动汽车的主要储能装置，是电动汽车的重要组成部分［1-2］。然而在实际使用过程中电池健康状态会逐渐退化，给电动汽车带来安全隐患和高额的运行维护成本［3-4］。因此，为给使用者提供合理的电池更换时间，保障系统正常运行，避免严重事故的发生，对电池剩余使用寿命（remaining useful life，RUL）预测展开研究十分必要。

近年来，由于粒子滤波（particle filter，PF）具有强大的非高斯、非线性问题处理能力，且能通过概率密度函数（probability density function，PDF）提供预测结果的不确定性表达而被广泛应用于锂离子电池RUL预测［5］。文献［6］中在利用双指数模型进行电池容量退化建模的基础上，引入传统PF算法实现电池RUL预测，并将RUL预测结果与扩展卡尔曼（extended Kalman filter，EKF）算法进行对比，结果表明PF算法比EKF算法更可靠。文献［7］～文献［9］中为提高传统PF算法的粒子抽样效率，充分利用历史数据，采用不同的方法重新获得重要性密度函数，得到改进的PF算法并结合双指数模型实现电池RUL预测。文献［10］中针对传统PF算法固有的粒子退化现象，引入启发式卡尔曼算法（heuristic Kalman algorithm，HKA）对PF进行优化后实现电池RUL预测，并将RUL预测结果与粒子群优化粒子滤波（particle swarm optimized particle filter，PSO-PF）算法进行对比［11-12］，验证表明其精度高于PSO-PF算法。文献［13］中在预测单颗电池RUL时，结合其他多颗电池的历史容量数据来改善传统PF算法中的粒子权重更新过程，使滤波过程中的粒子权重更加准确，从而提高RUL预测精度。总体而言，现有基于PF的电池RUL预测方法主要从重要性密度函数、粒子匮乏问题、粒子抽样效率、粒子权重精确度等方面对传统PF进行改进以提高电池RUL预测精度，但传统PF还存在重采样过程粒子多样性丧失的问题。

为此，引入线性优化重采样算法［14］，其主要思想是：在重采样过程中并未完全抛弃权值较小的粒子，而是将权值较小的粒子与权值较大的粒子进行适当的线性组合，产生新的粒子，从而避免权值较大的粒子被反复复制，使粒子分布更加接近真实的后验概率分布。在此基础上构建基于线性优化重采样粒子滤波（linear optimization resampling particle filter，LORPF）算法的电池RUL预测方法。该方法首先基于电池容量，利用双指数模型建立电池全寿命周期状态空间模型；然后通过LORPF算法对模型参数进行迭代更新，并利用更新后的状态空间模型不断外推电池容量直至寿命失效阈值；最后基于状态空间模型外推所得电池容量实现电池RUL预测以及预测结果的不确定性表达。

1 基于LORPF算法的RUL预测方法

基于LORPF算法的电池RUL预测方法（以下简称LORPF-RUL）流程见图1，具体步骤如下。

第1步：从电池老化数据库中提取电池容量数据并进行预处理。

第2步：设定预测起始点T，如T＝60表示将第60个循环之前的电池容量数据作为历史数据，从第60个循环开始，预测每一个循环的电池容量值。

第3步：利用双指数模型跟踪电池老化趋势建立电池老化模型，采用最小二乘法拟合电池老化模型参数初始值，其中，电池老化模型的状态转移方程为

量测方程为

式中：β1，k，β2，k，β3，k，β4，k为电池老化模型参数；k＝1，2，…，n为电池充放电的循环数；过程噪声υ1，υ2，υ3，υ4为高斯白噪声，均值都为0，方差分别为σ1，σ2，σ3，σ4；zk为循环k次后的电池容量，ωk为量测噪声，是均值为0、方差为σω的高斯白噪声。

第4步：设定RUL预测过程中的相关参数，包括粒子数目N、过程噪声υk的协方差Q、量测噪声ωk的协方差R、电池失效阈值zthres（一般设置为电池初始容量的70%～80%）。

第5步：利用预测起始点T之前的电池历史容量数据对T及其之后的历史容量数据进行状态跟踪，不断 更 新 电 池 老 化 模 型 参 数β1，k，β2，k，β3，k和β4，k，从而得到预测起始点T及其之后每个循环的电池容量预测值z＾k。

计算各粒子权重：

式中：xik为第k时刻的第i个粒子；ωik为第k时刻第i个粒子的权重；p（zk｜xik）为第k时刻第i个粒子对应的量测值的似然概率密度函数。

归一化权重：

更新粒子权重：

式中：xn为新的粒子；xα为权值较大的粒子；xs为权值较小的粒子；S为（xα-xs）的合适步长；H为对应的步长系数。若粒子的权值满足式（6），则归为抛弃组，若不满足式（6），则归为复制组，然后利用式（7）进行线性优化组合产生新粒子，得到新的粒子集合，更新电池老化模型参数：

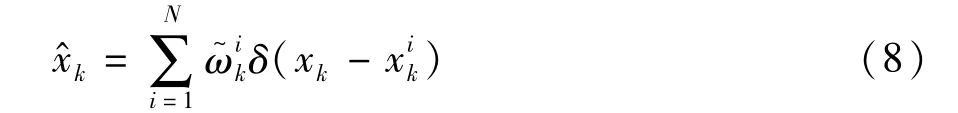
式中xik＝（βi1，k，βi2，k，βi3，k，βi4，k），i＝1，…，N；δ（·）为狄拉克函数。

预测电池容量：

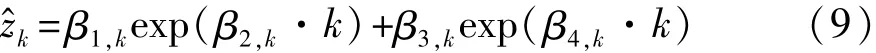
第6步：判断第k次的电池容量预测值z＾k是否达到阈值zthres，若达到阈值，计算电池RUL并给出PDF分布，算法结束。否则，重复执行第5步和第6步，直至z＾k达到失效阈值zthres。根据式（10）即可求得电池失效时的充放电循环数，再由式（11）可得到电池RUL的概率密度分布。

式中：Lik为电池循环k次时的RUL预测值；Lk为电池循环k次时的RUL真实值。

2 电池实验测试

电池实验测试包括NASA电池测试［15］和自主搭建实验平台的三星电池测试。

2.1 NASA电池实验测试

采用B0005，B0006和B0007号电池老化数据集。该实验平台使用额定容量为2 A·h的18650锂离子电池，在室温下对电池进行充电、放电和阻抗测试，具体步骤如下：

（1）充电 先将电池以0.75C（1.5 A）恒定电流模式充电至充电截止电压4.2 V，然后以恒定电压模式保持电池两端电压为4.2 V不变，直到电池充电电流下降到0.01C（0.02 A）时，充电结束；

（2）放电 将满充的电池以1C（2 A）恒流放电至预设截止电压，其中B0005，B0006和B0007电池放电截止电压分别为2.7，2.5和2.2 V；

（3）阻抗测试 采用0.1 Hz～5 kHz频率扫描锂离子电池测量电池阻抗。

将电池反复进行充放电循环测试，当电池容量退化到额定容量的70%，即电池容量从2 A·h退化到1.40 A·h时，停止实验。B0005，B0006和B0007号电池容量退化曲线如图2所示。

图2 NASA电池容量退化曲线

由图2可知，3个电池整体呈现出明显的退化特征，且局部存在容量再生现象。B0005和B0007号电池容量退化前期较为平缓，中后期退化加剧，两者退化趋势较为相似。而B0006号电池容量退化曲线波动较为剧烈，容量再生幅度较大，这可能是由于放电截止电压不同或电池单体的不一致性引起的差异。

2.2 三星电池实验测试

采用额定容量为2.6 A·h的三星ICR18650-26F型锂离子电池，编号S43。根据电池使用手册，参照文献［16］和文献［17］并考虑老化工况、温度等因素，模拟锂离子电池在电动汽车中的实际使用情况，设计多工况、多温度下的电池特性及老化实验，实验流程如图3所示，具体步骤如下。

（1）电池特性测试 分别在10，25和40℃下，先对电池进行容量测试：以恒流恒压（constant-current and constant-voltage，CC-CV）充电法满充并静置1 h后，再以0.2C恒流放电至放电截止电压2.75 V，视放出的容量为电池当前最大可用容量。然后将CC-CV法满充的电池进行一次简化的NEDC动态工况放电，直到电池端电压降至截止电压2.75 V，再以同样的充电方式和截止电压分别进行简化的UDDS和JP1015动态工况放电。电池在每种温度下的特性实验经历4个循环，3种温度下的特性实验共计12个循环。

（2）电池老化测试 为加速锂离子电池老化速率，将电池老化循环实验温度设置为45℃，先将电池以CC-CV法满充并静置1 h，然后以NEDC，UDDS和JP1015的叠加工况（图4）循环放电至截止电压，并重复进行3次。

图4 电池老化测试工况

（3）将上述10，25和40℃下特性测试和老化测试4个步骤重复循环进行，直至电池容量退化到额定容量的80%，即2.08 A·h时，停止实验。

当S43号电池容量小于等于失效阈值2.08 A·h时，共进行了37次25℃下的容量测试，相邻两次测试之间理论间隔15个循环。提取25℃下的S43号电池容量测试数据，得到电池容量退化曲线，如图5所示。可知S43号电池容量退化曲线整体呈现出明显的退化特征，大约在第200个循环前后出现容量再生现象，当电池容量退化达到失效阈值2.08 A·h以后，电池容量退化加速。

3 LORPF-RUL的验证与分析

为验证LORPF-RUL方法的有效性，分别采用NASA B0005，B0006，B0007号电池和25℃下的S43号电池根据图1所述流程进行RUL预测。

初始化LORPF算法：分别选取B0005，B0006，B0007号电池的第60循环、第80循环和第100循环作为预测起始点；选取S43号电池的第166循环、第256循环和第336循环作为预测起始点（大约选取寿命截止循环数的1／3，1／2和2／3为预测起始点，分别代表电池老化前期、中期和后期）。采样粒子数目N＝200；NASA电池容量失效阈值为1.40 A·h；S43号电池容量失效阈值为2.08 A·h；过程噪声vk的协方差Qk＝0.0001；量测噪声wk的协方差Rk＝0.0001。得到B0005，B0006，B0007和S43号电池预测结果，如表1所示。

由表1可知，4个电池在3种不同的预测起始点共计得到12组预测结果，RUL真实值落在95%置信区间的结果为9组，占全部预测结果的75%，所以在预测结果的不确定性表达方面，LORPF-RUL可以获得比较优异的预测性能。此外，对表1中的相对误差求平均值可得平均相对误差为4.657%，表明LORPF-RUL具有较高预测精度。同时，随着预测起始点后推，用于老化建模的已知历史容量数据点增多，LORPF-RUL在第3个预测起始点下（电池老化后期）的预测结果比前两个预测点（电池老化前中期）都要更接近真实RUL，误差更小。

图6和图7以定性的方式给出了B0005和S43号电池LORPF-RUL与基于传统PF（初始化参数设置与LORPF算法的初始化参数设置相同）的电池RUL预测方法（以下简称PF-RUL）的直观对比。

由图6（a）和图7（a）可知，在电池历史容量数据较少的情况下，LORPF-RUL预测精度仍高于PFRUL，且由图6（b）、图6（c）和图7（b）、图7（c）可知，随着老化建模的历史电池容量数据增多，虽然两种方法的电池RUL预测值都逐渐接近RUL真实值。但LORPF-RUL的PDF分布比PF-RUL更高、更窄，说明LORPF算法的预测结果比PF算法具有更高的精度和可信度。

为进一步评估LORPF-RUL的性能，以量化方式对LORPF-RUL和PF-RUL的预测结果进行对比，如表2所示。

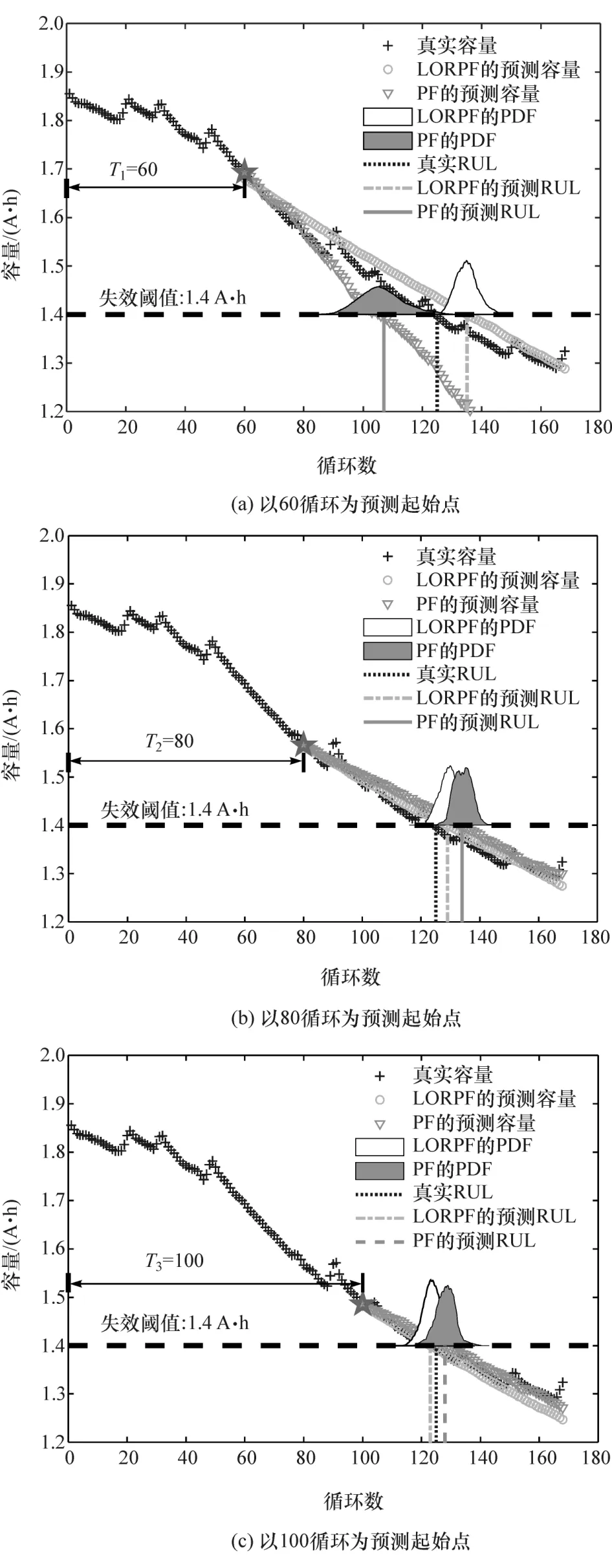
图6 基于B0005号电池数据的RUL预测结果对比

由表2可知，PF-RUL误差大于13个循环的结果为6组，占全部预测结果的50%，而LORPF-RUL只有2组误差大于13个循环，仅占全部预测结果的17%，且有7组误差不超过10个循环，占全部预测结果的58.3%。再分别对表中两种方法的预测误差求平均值，可得PF-RUL的平均误差为20.67个循环，而LORPF-RUL的平均误差仅为8.7个循环。其中B0006号电池在起始点为80循环时的RUL预测误差较大，是因为B0006号电池在第90个循环左右出现明显的容量再生现象，使后期老化速率与前期明显不一致，导致RUL预测误差较大。总而言之，LORPF-RUL相比于PF-RUL不仅预测误差波动小，且预测精度有很大提升，由此可知，所采用的LORPF算法能够有效预测电池RUL。

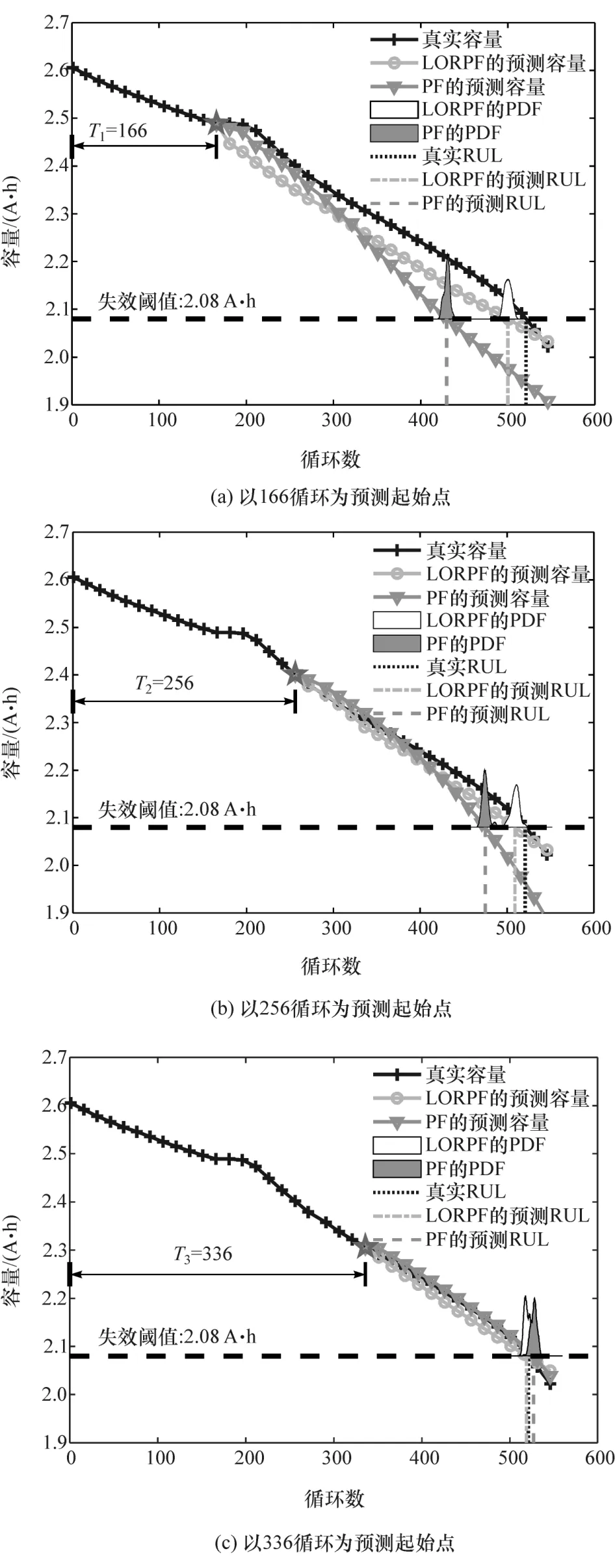
图7 基于S43号电池数据的RUL预测结果对比

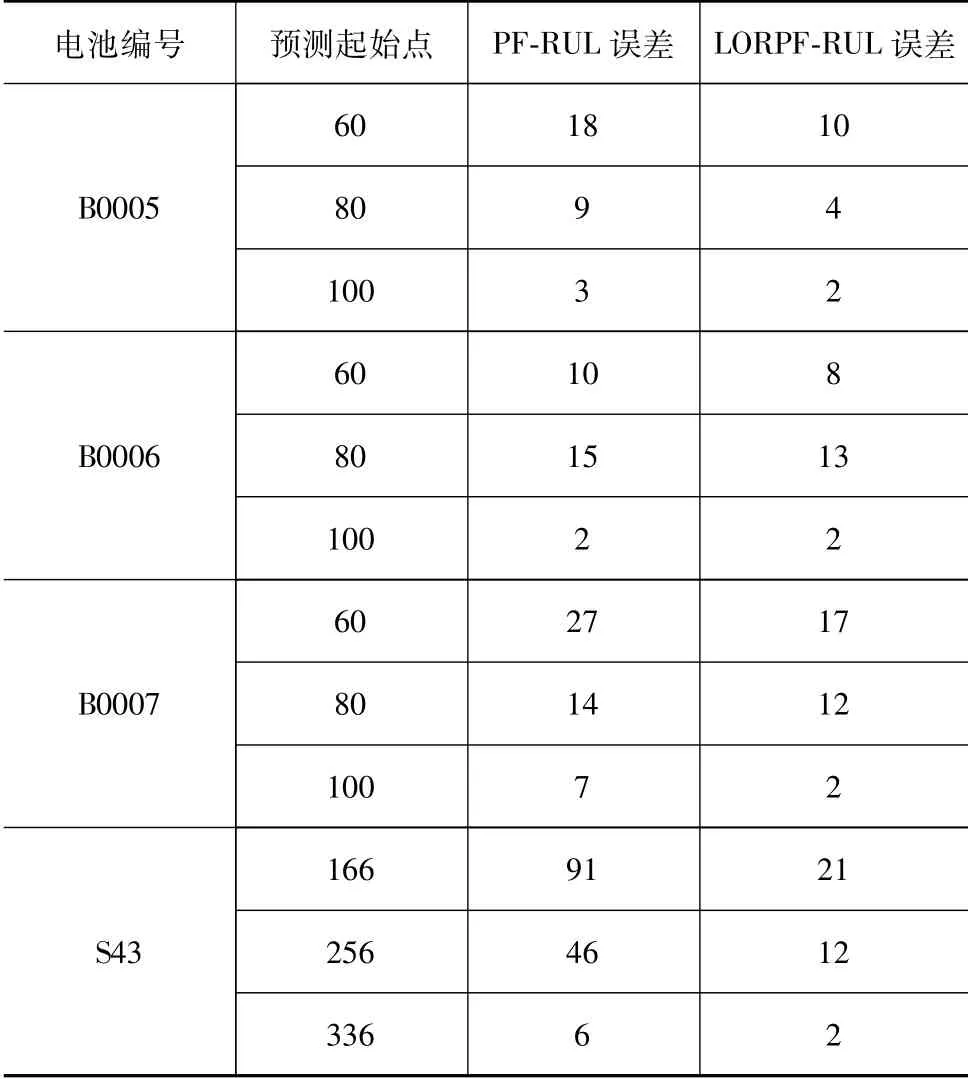
表2 LORPF-RUL与PF-RUL的预测误差对比

4 结论

为提高传统PF框架下的锂离子电池RUL预测精度，针对传统PF算法在重采样过程中存在的粒子多样性丧失问题，建立基于LORPF算法的电池RUL预测方法，并采用NASA电池数据和自主搭建实验平台电池数据对算法进行验证，得到以下结论。

（1）利用线性优化重采样思想解决传统PF算法在重采样过程中存在的粒子多样性丧失问题，提出构建基于LORPF算法的电池RUL预测方法。

（2）通过NASA电池数据和自主搭建实验平台电池数据对LORPF-RUL进行验证。结果表明线性优化重采样能够有效地缓解传统PF算法中粒子多样性丧失问题，LORPF-RUL相比于PF-RUL不仅具有更高的预测精度，预测误差不超过5%，且具有更好的不确定性表达能力。

现阶段，仅对传统PF算法进行改进的电池RUL预测方法在预测精度上仍存在提升的空间。由于双指数模型是严格单调的函数，而有些锂离子电池（例如NASA B0006）的部分容量退化趋势实际上是非单调的，甚至表现出强烈的波动（较严重的容量再生现象）。此时，双指数模型很难精确跟踪电池容量退化趋势，因此，在以后的工作中，将进行大量研究以开发出更稳健且能描述电池非单调退化趋势的新模型。