伴随发动机起动的混合动力模式切换控制
2020-01-04张幽彤单小明
杨 业,张幽彤,单小明
(1.北京理工大学清洁车辆实验室,北京 100081; 2.华北理工大学轻工学院,唐山 063000)
前言
由于环境和能源危机,混合动力汽车备受青睐[1-3]。多动力源是混合动力汽车最显著的特点,其关键技术直接决定了混合动力汽车的经济性、可靠性、安全性和舒适性。混合动力汽车运行过程中,为了提高燃油经济性,需要在各种运行模式之间频繁地转换,然而,模式转换常常伴随着发动机、离合器和电机的目标转矩突变,造成汽车传动系统的振动和冲击,从而影响汽车行驶的舒适性。
在模式切换过程中,转矩补偿控制策略是一种常用的转矩协调控制方法[4-5]。其利用电机的快速响应特性对发动机的输出迟滞转矩进行补偿,以减小模式转换过程的转矩波动,从而提高舒适性。文献[6]中提出了一种模型匹配控制方法,其控制思想类似于转矩补偿控制策略。Hwang等[7]针对混合动力离合器结合的模式切换过程,提出发动机和电机的动态转矩控制策略,即在离合器结合之前,采用发动机转速控制策略;在离合器接合过程中,采用电机转矩控制策略。Koprubasi[8]和赵治国等[9]采用基于混杂系统的无扰动切换控制算法,实现由纯电动起步到发动机参与驱动模式的混合动力模式切换仿真分析,验证了无扰动切换控制算法能够有效减少模式切换过程的冲击度。
清华大学童毅[10]和吉林大学严运兵等[11]针对并联混合动力中发动机与电机响应的差异问题,在整车转矩管理策略的基础上,提出了“发动机转矩开环+发动机动态转矩估计+电动机转矩补偿”的模式切换动态协调控制策略,解决模式切换中的动态差异造成的冲击问题。这种控制策略仍然是组合式的设计思维,依赖于对发动机动态转矩的精确估计,应用于涉及发动机起动过程的模式切换动态控制中的效果并不理想。近年来,相关学者采用动态协调控制策略对混合动力系统模式切换造成的冲击进行研究[12-14]。Kimura等[12]利用行星齿轮机构直接测量发动机转矩,然后采用电动机转矩对发动机转矩进行调整,较好地解决了动态模式切换过程中的发动机转矩估计和补偿问题。Ngo等[13]应用动态规划和最小值原理对发动机和电机转矩进行动态协调控制,提高了整车行驶平顺性。
目前的研究往往集中于降低系统状态切换频率或者直接采用电机转矩补偿的方式,一方面影响了经济性,另一方面也无法满足同轴并联结构形式下的状态切换控制需求[15-17]。已有研究应用系统理论对混合动力系统动态切换问题进行研究,但这些研究中所涉及的车辆都配置有ISG或BSG电机,能够在状态切换前将发动机起动。而本文中研究的同轴并联混合动力系统不单独配置发电机,也取消了专有的发动机起动机,这就需要建立一个考虑发动机起动的状态切换协同控制策略,针对发动机起动和并载进行全面系统化研究。
基于上述分析,本文中以同轴并联的混合动力系统为研究对象,引入状态空间理论,对模式切换前后各个状态进行数学表征,建立状态方程并进行适当的矩阵变换,以系统切换代价函数为优化对象,对各个状态切换过程进行优化求解,获取最优控制变量。从而建立系统的动态协同控制策略。
1 动力系统
1.1 动力系统结构
同轴并联混合动力客车动力总成包括:天然气发动机、离合器、电动机和自动机械式变速器(AMT),如图1所示。其中发动机和电机通过离合器同轴相连,发动机和电机既可单独驱动车辆,也可混合驱动车辆,并且兼具制动能量回收功能。

图1 单轴并联混合动力系统
根据同轴并联混合动力系统的结构图可知,该混合动力系统具有5种典型的工作模式,如表1所示:纯电动、发动机单独驱动、混合驱动、行车充电和制动能量回收模式。实际运行时,根据不同的工况,混合动力系统在各个模式之间来回切换,保证发动机的工作效率,从而降低油耗和污染物排放。不同模式切换过程中,由于发动机和电机、电机和摩擦制动系统的动态响应特性等差异,往往会引起驱动力或制动力输出的转矩和转速波动问题,从而造成车辆纵向冲击,其中,由纯电动模式切换到混合驱动模式时,伴随着发动机的起动和并载过程,对整车传动轴的冲击更为明显,因此,针对动力耦合过程中的冲击问题,本文中借鉴状态空间理论的基本思路,提出动态转矩协调控制策略,降低冲击,提高整车驾乘舒适性。

表1 同轴并联混合动力系统基本运行模式
1.2 动力系统模型
1.2.1 车辆纵向动力学模型
根据车辆行驶过程中的动力学平衡关系,车辆在车轮上需求的牵引力Ft为
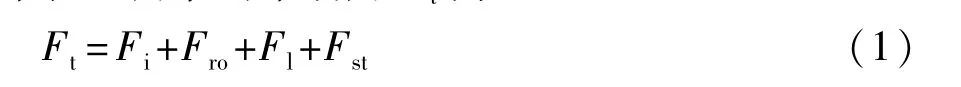
式中:Fi为车辆冲击力;Fro为滚动阻力;Fl为空气阻力;Fst为坡度阻力。它们可分别表示为

式中:m为整车质量;g为重力与质量比例常数(取9.8 N/kg);f为滚动阻力系数;ρ为空气密度;CD为风阻系数;Af为车辆迎风面积;α为坡道角度;vrv为车辆行驶速度。
由式(1)计算出车轮需要的牵引力后,可得到主减速器需求转矩:

式中:rwh为动态车轮半径;Jwh为车轮转动惯量;Twh,loss为车轮中转矩损失;wwh为车轮角速度;w·wh为车轮角加速度。
1.2.2 传动系统模型
传动系由离合器、变速器、减速器和半轴组成。其中,离合器模型根据其分离、滑摩、接合3种状态来建立。在分离状态下,动力传递为零;在接合状态下,动力等值传递;在滑摩状态下,传递的转矩计算如下:
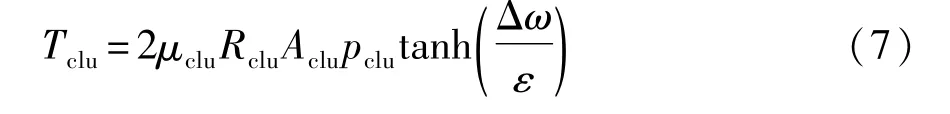
式中:μclu为动态摩擦因数;Rclu为摩擦盘的有效半径;Aclu为摩擦盘的有效摩擦面积;pclu为离合器接合压力;Δω为离合器主从动盘的相对滑摩速度;ε为转速阈值。
半轴对车辆动力传动系统的最低共振频率振动有重要影响,因此,半轴的动态特性如下:

式中:Khs为半轴的刚度;θhs为半轴的扭转位移;bhs为半轴的阻尼系数;Δωhs为半轴两端的速度差。
变速器在动力传动系统中占有重要的位置,其通过改变传动比来满足车辆在不同行驶条件下对牵引力的需求。减速器的作用是将变速器输出的转矩和转速传递到驱动轮,其结构和变速器类似,但传动比固定。因此,为了简化采用总传动比代替变速器和减速器。变速器输入端速度ωM与车轮转速ωW的关系可表示为

式中itr为传动系统总传动比。
1.2.3 发动机和电机模型
发动机和电机采用实验建模法。实验建模法简单有效,模型数据可以通过性能实验获得。在不考虑发动机的温度影响的情况下,依据选定的发动机万有特性和电机效率特性建立发动机模型和电机模型。图2和图3分别为天然气发动机万有特性图和电机效率特性图。
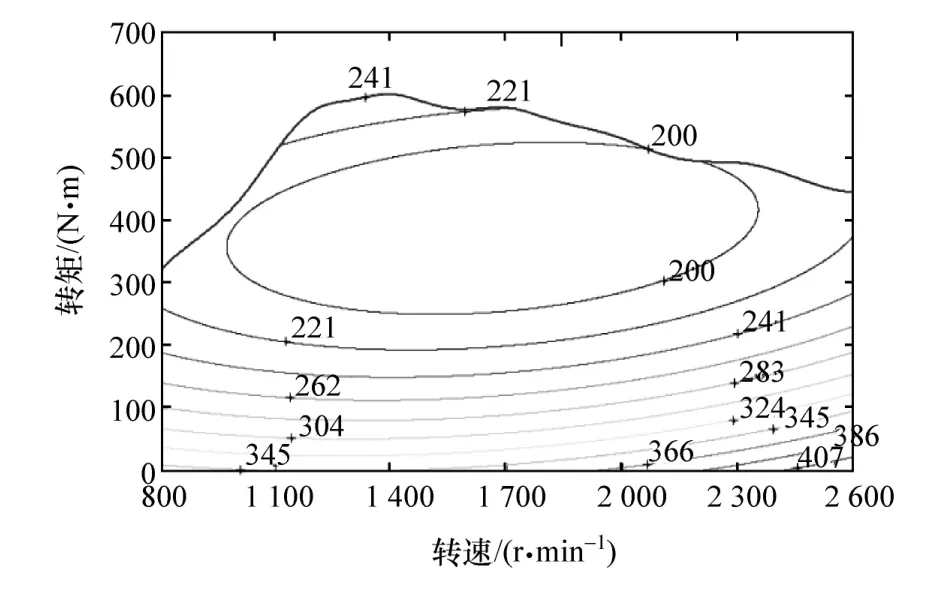
图2 天然气发动机万有特性图
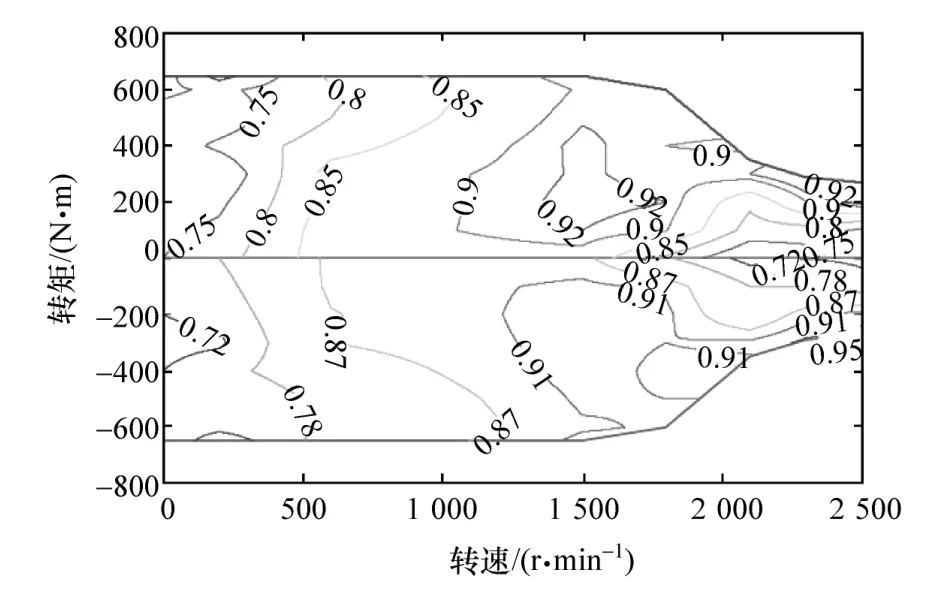
图3 电机效率特性图
2 控制策略
2.1 状态空间切换模型
针对所研究的同轴并联混合动力城市客车,采用状态空间切换控制理论对多模式切换过程进行分析。该问题的研究对象为一组通过状态相关微分方程表征的状态切换系统,包含m个不同状态,可表示为

式中∑i为整个动态切换系统的第i个状态。每一个状态都通过6元数组进行定义:
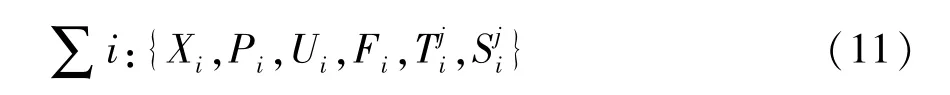
式中:Xi为相关的状态空间;Pi为输入变量的有限集;Ui为状态空间的控制变量;Fi为在第i个模式的状态空间Xi中描述连续演变的映射;Sji为第i个状态向第j个状态切换时开关信号;Tji为第i个状态向第j个状态切换时对应的切换规则。
在每一状态下建立一个从状态i到状态j的状态切换代价函数Jji,且有:

图4为状态空间切换过程的示意图。处于第i个状态的系统状态轨迹达到切换集合Sji后随即发生模态转换,如果满足了切换规则Tji,使状态从Xi切换到Xj,状态变换后,新的矢量场Fj控制着状态空间Xi向Xj的演变。

图4 状态空间动态切换过程示意图
根据同轴并联混合动力系统的结构特点,将纯电动模式向混合驱动模式切换过程划分为4个状态,分别为:发动机停机下的纯电动状态、离合器半接合发动机拖转状态、离合器接合发动机并载状态和完成并载进入混动状态等4个状态。其切换过程如图5所示,Xi分别用来描述4种模式所对应的状态空间。

图5 纯电动至混合驱动模式切换过程示意图
状态转移条件Sji定义为
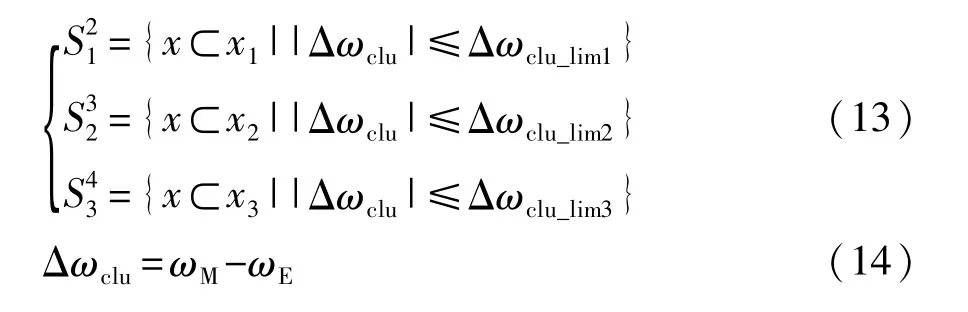
式中:Δωclu_lim1,Δωclu_lim2,Δωclu_lim3分别为离合器开始接合和接合完成时主、从动盘间的转速差的阈值,即当离合器主、从动盘转速差低于阈值Δωclu_lim1时,S21被触发,离合器开始接合,发动机处于拖转状态;当离合器主、从动盘转速差低于阈值Δωclu_lim2时,S32被触发,离合器接合完毕,发动机进入并载过程;当离合器主、从动盘转速差低于阈值Δωclu_lim3时,S43被触发,发动机并载完成,系统进入混合驱动模式。
选取发动机转速ωE、电机转速ωM、车轮转速ωW和半轴扭转位移θhs为状态变量,即

选取发动机转矩TE和电机转矩TM为状态变量,即
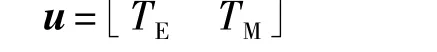
同轴并联混合动力系统模式切换过程的主要执行部件为离合器,切换过程中希望离合器快速平稳,其主动和从动盘的转速尽量同步,据此可以定义切换过程的代价指标函数为

式中:Δωhs为半轴输入输出速差,即半轴的偏转率;σ1,σ2,σ3和σ4为权重因子。
采用上述模型和代价指标函数对系统切换过程进行表征后,动态过程平顺性控制问题就可以简化为对代价指标的最小化问题。通过对J21的最小化,使离合器拖起发动机所用时间最短,通过最小化J32实现发动机和离合器转速的快速收敛,通过最小化J43实现变速器和驱动轴等动力传动系统的输出转矩在离合器接合完成后保持稳定状态。
2.2 模式切换
2.2.1 发动机停机下的纯电动状态
车辆工作于纯电动模式时,发动机停机,离合器处于分离状态,电机单独驱动车辆,此状态下,各个状态变量的动力学特性可表示为
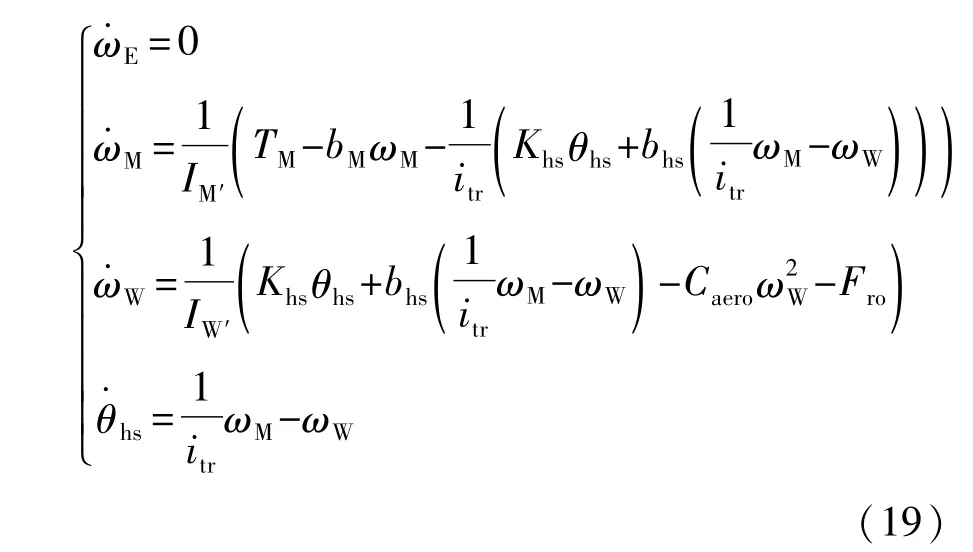
式中:IM′为永磁同步电机及其固连机构的综合转动惯量,包含转子转动惯量、离合器的电机端(摩擦片)转动惯量和自动变速器输入端的转动惯量;IW′为车轮转动惯量和车轮惯性等效转动惯量之和;bM为电机输出轴等效阻力。
状态1向状态2切换时,控制算法的核心是最小化代价指标函数J21,即在快速响应的前提下尽可能减小发动机拖起的时间。在此阶段,由于离合器从分离状态变为部分接合状态,发动机仅作为一个与转速相关的负载出现,因此驱动电机除了满足整车动力需求外,还需要输出额外的转矩用于克服发动机阻力矩。此时,发动机和电机转矩输出应满足:

式中:Tdem为整车需求转矩;bE为发动机输出轴的等效阻尼。
2.2.2 离合器半接合发动机拖转状态
对离合器半接合状态进行控制的目标是使发动机转速能迅速升至目标起动转速,并尽量降低此过程中的转矩振动。在离合器接合过程中发动机迅速转动,但是由于此时发动机仅作为负载,未与下游动力系统发生动力耦合。此状态下,各个状态变量的动力学特性可表示为

对应的状态方程为

其中

当状态空间发生转移时,对于性能指标矩阵z2则有

其中
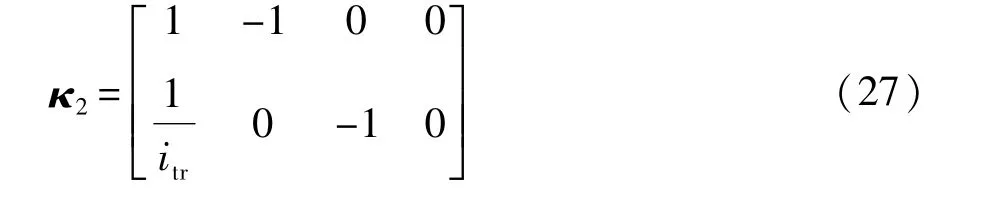
按照等式约束下的拉格朗日型最优解条件,可以求得控制变量u2使代价指标函数J32达到最小化:

2.2.3 离合器接合及发动机并载状态
对离合器接合过程进行控制的目标是使发动机转速能迅速与驱动电机转速匹配,即离合器主、从动盘的转速迅速达到一致并尽量降低此过程中的转矩振动。由于离合器接合过程的滑摩特性,动力传递要经历一个非线性延迟过程,发动机转矩随着离合器的接合逐渐与后续动力系统耦合,而驱动电机的转矩逐渐降低,以保证并载过程中相对稳定的动力输出。此状态下,各个状态变量的动力学特性可表示为

该过程的状态方程为

同样的,可以求得控制变量u3使代价指标函数J43达到最小化:
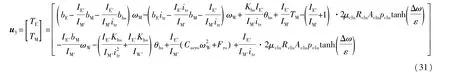
2.2.4 混合驱动状态
发动机并载过程结束后,整车进入混合驱动模式,发动机与驱动电机共同驱动车辆运行。此状态下,各个状态变量的动力学特性可表示为

式中:IE′为自动变速器输入轴前端的综合转动惯量,包含发动机、离合器、永磁同步电机和变速器输入端的转动惯量。
进入混合驱动模式后,发动机输出端与电机输入端通过离合器刚性连接,转速相同,发动机和电机的共同输出转矩满足车辆转矩需求。

车辆运行于混合驱动模式时,整车控制单元根据当前工况由上层能量管理策略分配转矩指令,发送给电机和发动机。因此,此时的控制规则可定义为

式中Tes为整车能量管理策略分配的发动机转矩。
3 实验研究
3.1 台架组成
为验证本文的控制策略,建立同轴并联混合动力系统实验台架,台架布置方案如图6所示。本文中设计的混合动力系统实验台架采用同轴的方式将天然气发动机、永磁同步电机、自动变速器和测功机连接起来。实验台架布置实物如图7所示。除以上动力连接部件之外,动力系统实验台架还包括动力电池组及其管理系统、冷却水控制系统、电机控制器、电控单元在线标定系统、总线监测系统和油门踏板等信号的模拟装置等,动力系统主要部件参数如表2所示。

图6 布置方案

图7 实验台架实物图

表2 混合动力系统主要部件及参数
3.2 台架实验
为验证本文中提出的控制策略的有效性,分别采用传统的电机转矩补偿策略和本文中所设计的动态协调控制策略进行对比实验,获取相应的实验曲线。
模式转换过程中的评价指标主要包括乘坐舒适性和快速性。乘坐舒适性是指在模式转换过程中,由于车辆加速度变化引起的冲击,它可表示为车辆加速度的变化率,即

式中:J为车辆冲击度,m/s3;a为车辆加速度,m/s2。冲击度越小,车辆驾驶舒适性越好。
快速性是指模式转换的持续时间,时间越短,模式切换速度越快。
3.2.1 电机转矩补偿策略
图8和图9为电机转矩补偿策略下的实验结果。具体实施步骤采用文献[18]中的方法,即离合器接合之前无控制策略,离合器接合后,利用电机的快速响应特性对发动机的输出转矩进行补偿。如图9(b)所示,离合器从18 s开始接合,到19.2 s接合完成,共用时1.2 s。在离合器接合过程中,电机在驱动车辆的同时拖转发动机,由于发动机起动阻力矩和电机补偿的时间差影响,电机转速及车速被短暂的下拉,出现类似于制动的现象,整车平顺性瞬间恶化,出现较大的冲击。从图8中可以看出平顺性恶化的时间大约持续0.7 s左右,但是由于冲击幅度较大,会导致车辆驾驶员和乘客感受比较明显。

图8 电机转矩补偿策略下的速度曲线
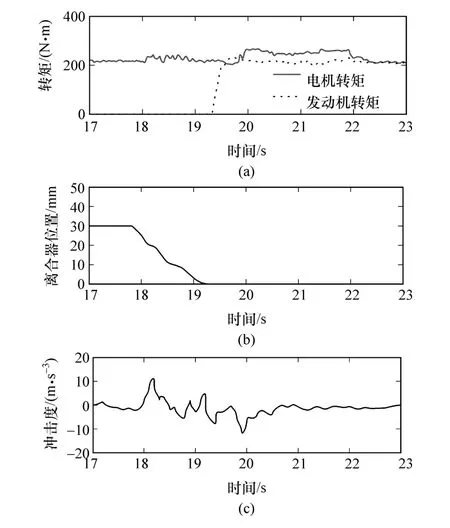
图9 电机转矩补偿策略下的实验结果
如图9(c)所示,冲击主要出现在离合器接合阶段、发动机起动阶段和发动机转矩并载阶段。其中最大冲击度为-14.2 m/s3,出现在离合器初始接合阶段。离合器接合过程经历滑摩阶段和锁止阶段。在滑摩初始阶段,离合器快速接合,离合器摩擦转矩增大,快速增加的摩擦转矩作为振动激励源作用在传动轴上,因此,振动被激发。此外,从滑摩阶段过渡到锁止阶段时由于离合器摩擦转矩突然改变,这种变化会对传动轴产生另一个大的冲击,所以振动会持续到锁止阶段。从图9(a)中可以看出,在离合器完全接合以后,发动机转速才达到起动转速,即发动机在19 s才开始喷油点火,此时,发动机起动转矩会造成动力传动系统振动,后续的发动机转矩并载也会引起冲击。到20.5 s左右,发动机并载完成,整车进入混合驱动模式。整个模式转换时间共历时2.5 s。
3.2.2 动态协调控制策略
图10和图11为动态协调控制策略下的实验结果。如图10所示,在模式切换过程中电机转速有瞬间的上拉趋势,车速也有小的波动。但从整个状态切换过程来看,整体幅度远低于传统的电机转矩补偿策略的情况。如图11(c)所示,整个切换过程的冲击度控制在10 m/s3以内,满足整车平顺性需求。其冲击可分成3个阶段。
(1)离合器滑摩阶段
滑摩阶段的起始点为半接合点,即摩擦转矩与发动机阻力转矩相等的位置点。半接合点之后,从动盘开始转动并逐渐加速。发动机转速随着离合器转矩的增大不断上升,直到达到发动机目标起动转速。由于离合器接合过程短暂,可认为整车需求转矩为定值,且动力性损失可暂时忽略,故电机只需要输出部分定值转矩给轮轴,另一部分转矩用以补充给离合器转矩将发动机快速拖起。如图11(b)所示,此时电机转矩为280 N·m,而发动机在转速同步前全程不输出转矩。因此,发动机和电机滑摩过程完全依赖于离合器转矩大小,且冲击度也只与离合器转矩相关。

图10 动态协同控制策略下的速度曲线
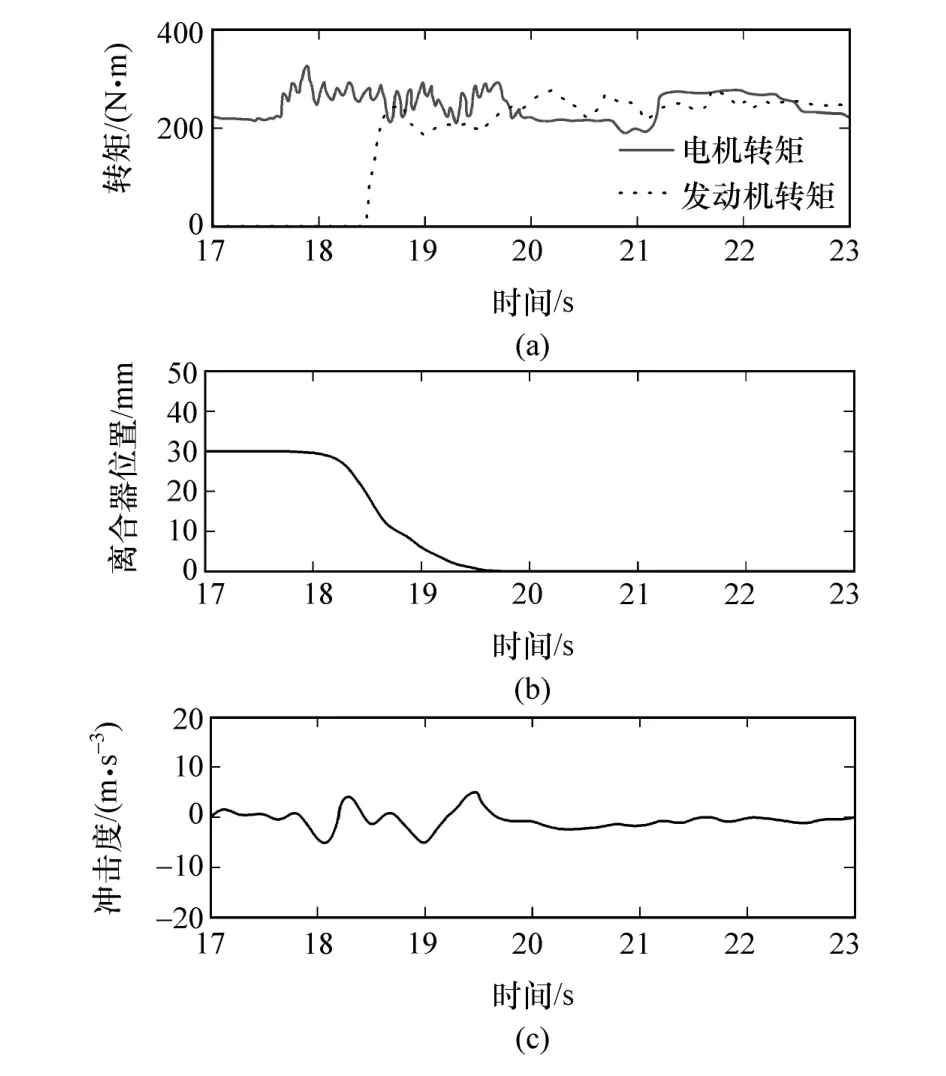
图11 动态协同控制策略下的实验结果
(2)发动机起动阶段
发动机在800 r/min左右开始喷油点火,如图11(a)所示,从18.4 s开始起动到18.7 s起动完成。发动机在起动过程中,会产生转矩脉动,这些脉动转矩由泵气转矩、活塞的摩擦转矩、往复惯性矩等产生。随着发动机起动,脉动转矩会引起动力传动系统振动,进而导致车辆冲击。
(3)发动机并载阶段
发动机起动完成后,发动机和电机按照上层能量管理策略输出相应的转矩共同驱动车辆,由于发动机和电机动态特性的差异,发动机不能及时响应设定的目标转矩,导致动力输出端转速波动,从而引起较大的冲击。由于采用了动态协调控制策略,电机转矩及时介入,弥补了发动机转矩不足,因此冲击度减小。如图11(c)所示,在模式转换过程中3个阶段都有冲击发生,其中,离合器接合阶段中的冲击最大,达到-7.2 m/s3。
表3为两种实验方案所产生的模式转换时间和最大冲击度对比表。从表3中可以看出,无论是从模式转换时间方面还是最大冲击度方面,本文中提出的动态协调控制策略比传统的电机转矩补偿策略控制效果要好很多,在改善车辆冲击度方面作用明显,冲击度几乎下降了一半。

表3 实验结果对比
4 结论
针对同轴并联混合动力客车,分析了从纯电动模式向混合驱动模式的动态切换过程,基于状态空间理论将模式转换过程划分为4个子状态,设计了动态协调控制策略。以整车运行纵向冲击度和模式切换时间为评价指标,通过台架实验对所提出的动态协调控制策略进行验证,并与传统的电机转矩补偿策略进行对比。实验结果表明,所设计的控制策略有效抑制了转速波动,缩短了模式切换时间,减小了整车纵向冲击度,改善了驾驶性能。
由于同轴并联混合动力客车工作模式较多,在实车运行中发现:纯电驱动至混合驱动模式的切换过程驾驶性问题较为突出,且该过程伴随离合器、电机及发动机状态的变化,故本文中仅研究了纯电动驱动至混合驱动模式的单向切换过程,没有考虑其它模式切换过程,系统地解决不同驱动及制动模式间的切换问题,这将是下一步研究的主要内容。
