洪水频率分析中目标函数的统计试验研究

康 有，夏传清，马顺刚

(中国电建集团成都勘测设计研究院有限公司，四川成都610072)

1 研究背景

洪水频率分析(Flood Frequency Analysis，FFA)是把洪水作为随机事件，采用频率分析途径预测洪水极值事件发生的量级和频率，以确定水利水电工程在设计标准下工程规模的核心技术[1]。常根据实测洪水、历史洪水或古洪水等资料估计洪水理论总体分布参数，为水利水电工程提供给定重现期下合理的洪水设计值，其实质是根据设计流域内某水文站的洪水资料进行统计分析，利用实测或调查洪水数据拟合理论总体分布曲线，并作大幅度外延[2-3]。

洪水频率分析计算过程主要包括样本抽样、线型选择、参数估计、抽样误差和区域分析等。参数估计是其最关键的技术环节，其计算精度直接影响洪水设计值的可靠性[4]。国内外水文学者对参数估计方法进行了大量研究，并取得了系列重要成果。我国设计洪水计算规范推荐采用适线法(Curve Fit，CF)估计参数值，以P-Ⅲ型分布作为理论总体分布，适线准则(即目标函数)采用离差平方和准则或离差绝对值准则，绘点位置采用频率期望值公式[5]。研究表明，适线法中目标函数的选择对确定洪水设计值至关重要，不同的目标函数会得到完全不同的频率设计值。

由于实测样本点据在洪水频率曲线拟合过程中的重要程度不同，水文工作者又提出了加权适线法，采用权重函数确定各个实测洪水样本点据在目标函数中权重，尽量照顾频率曲线的中上部点据[6]。影响各样本点据的权重级别的因素主要包括资料精度、误差分布、适线目的等。一般假定各样本点据偏离最优频率曲线的离散程度服从正态分布，权重函数采用模糊隶属度函数、高斯函数等[7]。而各种权重函如何选取及其参数取值往往取决于水文工作者的经验，难以进行定量分析，存在较大的不确定性。

文献[8]对比分析了基于数值次序统计量的期望值、中值、众值和频率次序统计量的期望值等共计4种绘点位置的优化适线法的统计特性，结果表明基于数值次序统计量期望值的洪水频率分析方法(以下简称“NOES”)具有优良的统计特性，并构造一种加权离差绝对值和作为目标函数，其权重函数采用给定频率P设计值的标准差倒数。NOES方法没有综合对比分析基于各种目标函数的洪水频率分析方法的优劣，其目标函数的选取缺乏一定的依据。

本文采用P-Ⅲ型分布作为洪水理论概率分布，系统阐述了洪水频率分析中各类目标函数和权重函数，采用统计试验途径研究基于各种目标函数和权重函数的NOES方法的优劣，优选出精度高且稳健性优良的目标函数。以雅砻江流域甘孜水文站设计洪水为例，计算不同目标函数和权重函数组合下的洪水设计值，以期为雅砻江流域水利水电工程规划设计提供更加合理可靠的设计洪水依据。

2 目标函数计算方法

2.1 基本原理

NOES方法假定所研究的洪水随机变量X服从P-Ⅲ型分布，记作X～Γ(x;a，α，β)，其统计参数为Ex、Cv、Cs。假设洪水随机变量X的简单随机样本为(X1，X2，…，Xn)，则第m项数值次序统计量X(m)为(x1，x2，…，xn)中从大到小进行排列后(x(1)≥x(2)≥…≥x(n))的第m项。即，X(m)=x(m)；其概率密度函数f(m)(x)、期望值E(X(m)) 、标准差Std(X(m))、信息熵Ent(X(m))计算公式分别为

[1-F(x)]m-1f(x)

(1)

(2)

Std(X(m))=E[(X(m))2]-[E(X(m))]2

(3)

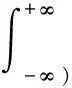
(4)

统计参数为目标函数达到最小值时所对应的优化变量值。洪水频率分析中目标函数为

(5)

式中，θ为统计参数(即Ex，Cv及Cs)；x(m)为经从大到小排序后第m个洪水样本(m=1，2，…，n)；E(X(m)，θ)为第m项数值次序统计量X(m)的期望值，即理论频率曲线上绘点位置的纵坐标值；Wm为权重函数；m为经从大到小排列后的样本次序；n为洪水样本序列容量。

2.2 无权目标函数

洪水频率分析本质上属于回归分析，其目标函数(Objective Function)即为统计学中回归分析的损失函数(Loss Function)，是一种衡量系统在不同参数组合下的损失和错误程度的函数。目标函数是用来衡量模型的预测值与真实值的不一致程度，它是一个非负实值函数，其值越小，表示该方法的精度越高。本文结合回归分析中各类损失函数，构建了以下8种无权目标函数(见表1)：

(1)平均绝对误差(Mean Absolute Error，MAE)是预测值与真实值之间误差绝对值的平均值。

(2)平均绝对根误差(Root Mean Absolute Error，RMAE)是预测值与真实值之间误差绝对值的平均值的平方根。

(3)平滑平均绝对误差(Smooth Mean Absolute Error，SMAE)为了增强平方误差，提高对离群点的鲁棒性而提出的；当误差很小时，SMAE是平方形式的；当误差很大时，SMAE是绝对值形式的；SAME计算公式中含有一参数δ。当δ→0时，SAME接近MAE，当δ→∞时，SAME接近MSE。

(4)两权平均绝对误差(Two Weight Mean Square Error，TWMAE)是分配预测值小于真实值的点据和预测值大于真实值的点据这两部分点据不同的权重，再计算误差绝对值的平均值。

(5)四权平均绝对误差(Four Weight Mean Square Error，FWMAE)是分配预测值小于真实值且频率小于90%的点据、预测值小于真实值且频率大于90%的点据、预测值大于真实值且频率小于90%的点据、预测值大于真实值且频率大于90%的点据这四部分点据不同的权重，再计算误差绝对值的平均值。

(6)均方误差(Mean Square Error，MSE)是预测值与真实值之间误差平方的平均值。

表1 洪水频率分析中目标函数计算公式

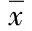
(7)均方根误差(Root Mean Square Error，RMSE)预测值与真实值之间误差平方的平均值的平方根。

(8)对数双曲余弦误差(Log Cosh Error，LCE)是预测值与真实值之间误差的双曲余弦的对数。

当预测值等于实测值时，损失函数达到其最小值0，取值范围为0至∞。图1给出了7种目标函数的变化情况(除FWMAE之外)，其中实测值为100，预测值在-80～120之间。

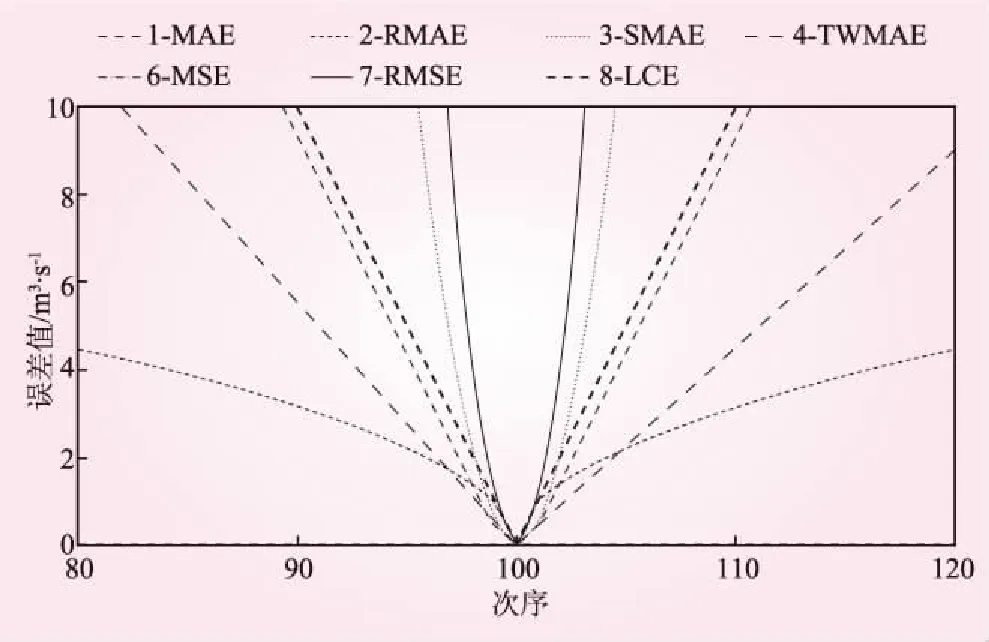
图1 各目标函数变化规律示意

2.3 加权目标函数

洪水频率分析的目的是计算稀遇频率洪水设计值。在实际工作中，经验适线法往往照顾频率曲线上端部分的点据，相当于增加大洪水点据在目标函数中的权重；也就是次序越小，其点据的权重越大[9]。另一方面，大洪水点据的离散程度也会增大，带来了更多的不确定性；也就是次序越小，其点据的权重越小。本文构建了四类加权目标函数(见表2)。

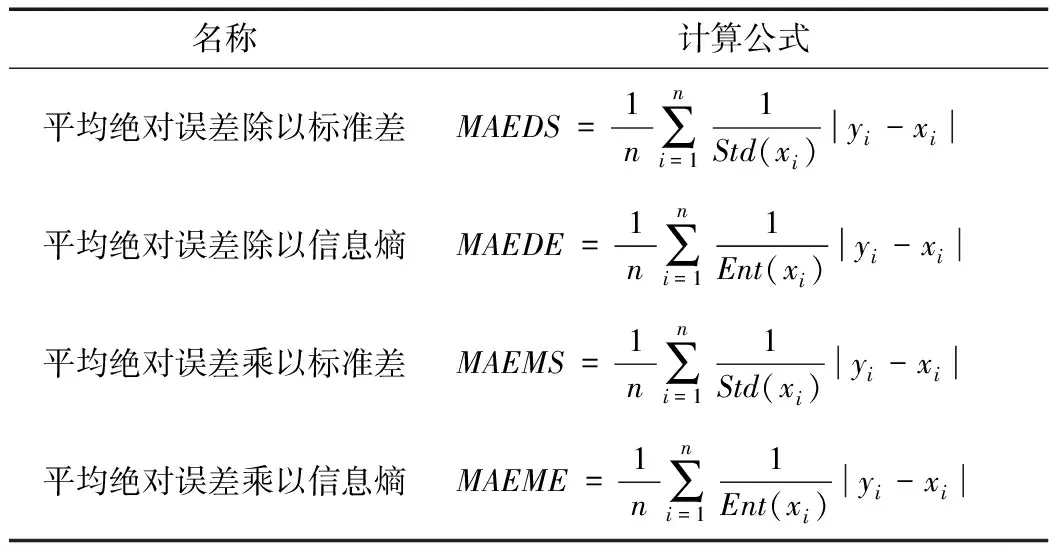
表2 洪水频率分析中加权目标函数统计

设P-Ⅲ型分布的参数Ex=100、Cv=0.5、Cs=1.5，洪水随机变量X的简单随机样本为(X1，X2，…，Xn)，计算第m项数值次序统计量X(m)的期望值E(X(m))、标准差Std(X(m))、信息熵Ent(X(m))，并绘制样本系列的经验概率密度函数和理论概率密度函数，以及次序统计量X(m)的概率密度函数f(m)(x)，见图2。

图2 数值次序统计量标准差和信息熵变化规律示意

由图2可知，随着次序m的增大，标准差和信息熵均减小；且在次序m较小时，减小趋势的梯度更大。图3给出了在给定总体分布参数的情况下前5个次序统计量的X(m)的概率密度函数，随着次序m的增大，期望值E(X(m))和实测值x(m)的绝对误差越来越大。

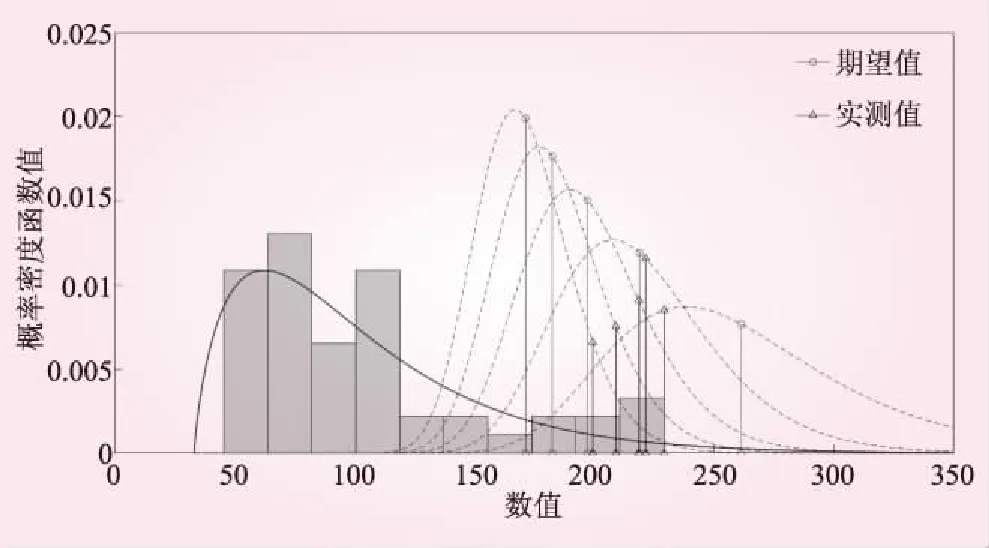
图3 数值次序统计量概率密度函数示意

表3 参数估计方法优劣评价指标及其含义

注：Ns表示统计试验的次数；x表示理论值；yi表示第i次的预测值。

3 目标函数统计试验

3.1 统计试验方法

构造一种基于拉丁超立方抽样、随机抽样的统计试验方法(即Latin Hypercube Sampling & Monte Carlo Statistical Test，简称“LM”)，在一定频率范围内生成服从指定分布(如P-Ⅲ型分布)的在有限频率区间内的洪水模拟序列，计算各种统计参数值和频率设计值，以检验不同参数估计方法的优劣[10～11]。LM统计试验方法计算步骤如下：

(1)将区间[Pmin，Pmax]等间隔分成10×n等份，并假设频率P在每一个小区间上服从均匀分布，其中Pmin=1/(n×1.5+1)，Pmax=1-Pmin。

(2)在每一个小区间上利用“乘同余法”产生10个服从均匀分布[Pmin，Pmax]的随机数Mt。

(3)从生成的10×10×n个均匀随机数Mt中随机选取n个随机数ut，并将其顺序随机打乱。

(4)利用“反函数插值法”转换为指定洪水频率分布函数F(x)的随机数xt=F-1(ut)；即根据洪水频率理论分布的总体参数Cs和均匀随机数ut(相当于频率P)计算P-Ⅲ型分布对应的ΦtΦt值。

(5)经算式xt=Ex×(1+Φt×Cv)，即可生成给定统计参数的P-Ⅲ型分布的连序洪水随机模拟系列(长度为n)，作为实测洪水样本系列。

(6)参数估计首先采用线性矩法初估参数值，然后采用NOES方法计算其最终值。其中，优化变量选取Ex、Cv与Cs/Cv，适线准则采用相应的目标函数，优化算法采用SCE-UA优化算法。

3.2 优劣评价标准

以参数值和设计值的无偏性及有效性为依据综合评价各种参数估计方法的优劣[12]。无偏性指标采用标准平均绝对误差(NMAE)，NMAE为正值表示设计值偏大；反之则偏小；其绝对值越小，则表示该方法的无偏性越好。有效性指标采用标准均方根误差(NRME)，NRME值越小，则表示该方法的有效性越好，具体见表3。

3.3 统计试验方案

根据大量流域水文站的实测洪水序列的统计参数规律和统计试验的实际需求，设定P-Ⅲ型分布统计参数方案编号依次为A、B、C、D、E，总体分布参数的取值分别为Ex=100，Cv=0.3、0.4、0.5，Cs=2.5×Cv、3.0×Cv、3.75×Cv、4×Cv、5×Cv，具体见表4。各组方案的统计试验次数Ns取500次，样本容量n取50，设计频率P取1%，0.5%，0.2%，0.1%。

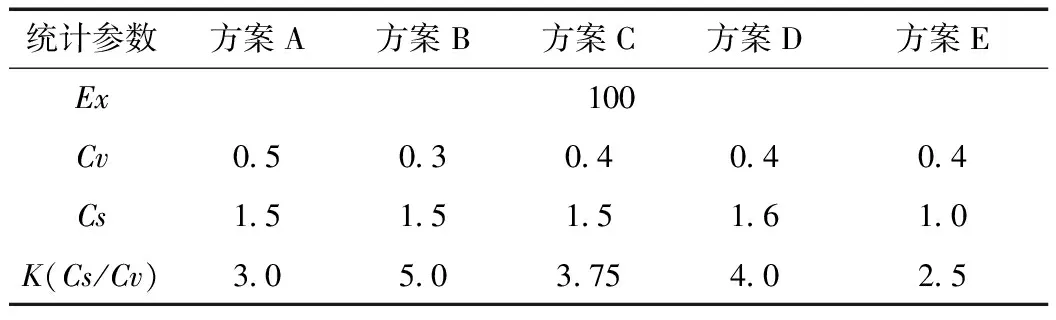
表4 统计试验选用的洪水频率分布统计参数

3.4 无权目标函数试验结果分析

采用基于MAE、RMAE、SMAE、TWMAE、FWMAE、MSE、RMSE、LCE共8种目标函数的NOES方法，分别计算基于5种统计参数方案共计30种统计试验方案的统计参数值(包括Ex、Cv与Cs)和洪水设计值XP(P取1%，0.5%，0.2%，0.1%)，以检验基于不同目标函数的NOES方法的无偏性和有效性。

(1)参数值统计试验结果。采用LM统计试验方法计算基于8种目标函数的NOES方法的参数值统计特性，见图4。从统计参数值的无偏性来讲，RMAE目标函数最优；且偏态系数Cs的NRMSE的绝对值最大，其无偏性最差。从统计参数值的有效性来讲，TWMAE目标函数最优；且偏态系数Cs的NRMSE的绝对值最大，其有效性最差。

图4 NOES方法的统计参数值无偏性和有效性

(2)设计值统计试验结果。采用LM统计试验方法计算基于8种目标函数的NOES方法的设计值统计特性，见图5。

图5 NOES方法的频率设计值无偏性和有效性

从频率设计值的无偏性来讲，RMAE目标函数最优；且随着频率P的减小，NMAE的绝对值增大，频率设计值的无偏性逐渐变差。从频率设计值的有效性来讲，TWMAE目标函数最优；且随着频率P的减小，NRMSE的绝对值增大，频率设计值的有效性逐渐变差。

3.5 加权目标函数试验结果分析

采用基于MAE、MAEDS、MAEDE、MAEMS、MAEME共5种目标函数的NOES方法，分别计算基于5种统计参数方案共计30种统计试验方案的统计参数值(包括Ex、Cv与Cs)和洪水设计值XP(P取1%，0.5%，0.2%，0.1%)，以检验基于不同加权目标函数的NOES方法的无偏性和有效性。

(1)参数值统计试验结果。采用LM统计试验方法计算基于4种加权目标函数的NOES方法的参数值统计特性，见图6。从统计参数值的无偏性来讲，MAEDS目标函数最优；且偏态系数Cs的NMAE的绝对值最大，其无偏性最差。从统计参数值的有效性来讲，MAEDE目标函数最优；且偏态系数Cs的NRMSE的绝对值最大，其有效性最差。

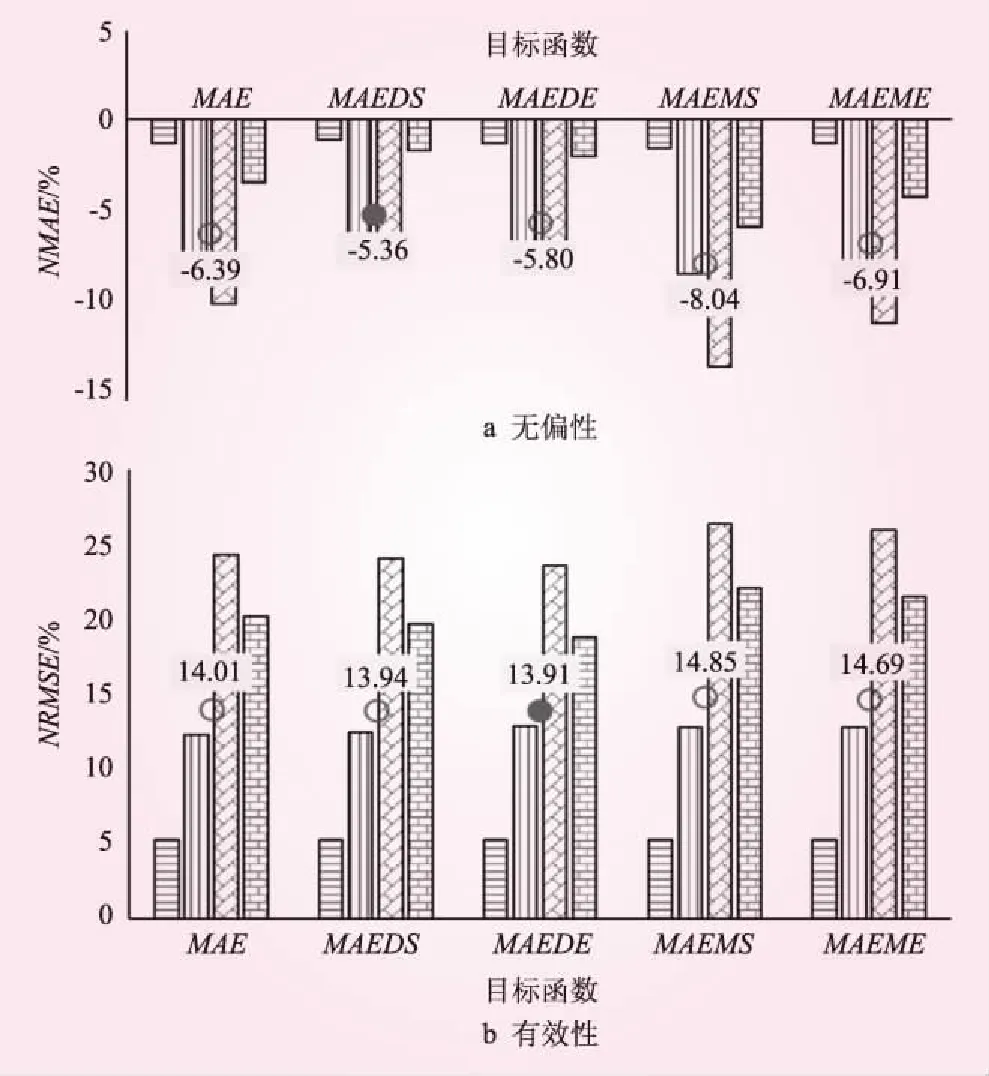
图6 基于不同加权目标函数的NOES方法的统计参数值无偏性和有效性

(2)设计值统计试验结果。采用LM统计试验方法计算基于5种加权目标函数的NOES方法的设计值统计特性，见图7。从频率设计值的无偏性来讲，MAEDS目标函数最优；且随着频率P的减小，NMAE的绝对值增大，频率设计值的无偏性逐渐变差。从频率设计值的有效性来讲，MAEDS目标函数最优；且随着频率P的减小，NRMSE的绝对值增大，频率设计值的有效性逐渐变差。

图7 基于不同加权目标函数的NOES方法的频率设计值无偏性和有效性

3.6 对比分析

从图4、5可知，从统计参数值和频率设计值的无偏性和有效性来讲，采用平均绝对根误差RMAE作为洪水频率分析的目标函数，可以有效减少洪水设计值的无偏性。从图6、7可知，从统计参数值和频率设计值的无偏性和有效性来讲，采用平均绝对误差除以标准差MAEDS作为洪水频率分析的目标函数，可以有效提高洪水设计值的有效性。在洪水频率分析目标函数的合理选取中，目标函数的选择取决于许多因素，包括是否有离群点、参数估计方法、误差分布规律等，没有一个通用的目标函数可以适用于所有统计参数的求解。综合分析，从统计参数值、频率设计值的无偏性和有效性整体上来讲，采用平均绝对根误RMAE为目标函数的NOES方法整体上精度高且稳健性优良，尤其在设计值无偏性上的优势更为明显。

4 实例分析

4.1 基本资料

雅砻江流域位于青藏高原东部，为金沙江第一大支流，干流河道全长1 535 km，流域面积12.8万km2。雅砻江流域甘孜水文站控制流面积为3.3万km2，自1952年4月设站至今。经插补延长后，采用年最大值抽样法(Annual Maximum Sampling，AMS)获得甘孜站1952年～2015年共计64 a的洪水年最大值系列(见图8)。

4.2 设计洪水

根据甘孜站1952年～2015年共计64 a的洪水年最大值系列，以P-Ⅲ型分布作为理论总体分布，首先采用线性矩法计算统计参数初始值；然后采用NOES方法分析计算统计参数值，优化变量选取Ex、Cv与Cs/Cv，适线准则采用MAE和RMAE目标函数，优化算法采用SCE-UA算法；计算给定频率P(1%、0.5%、0.2%和0.1%)的设计洪水XP，具体见图9、10。

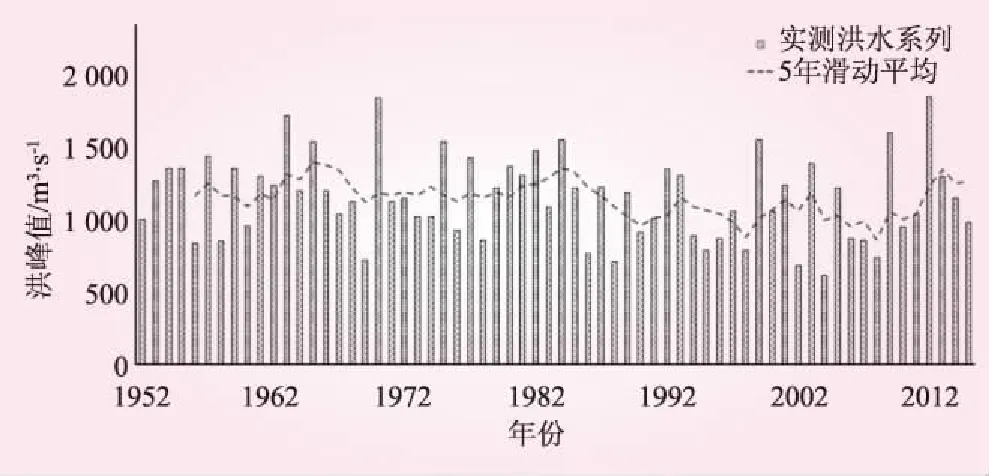
图8 雅砻江流域甘孜站洪水样本系列示意

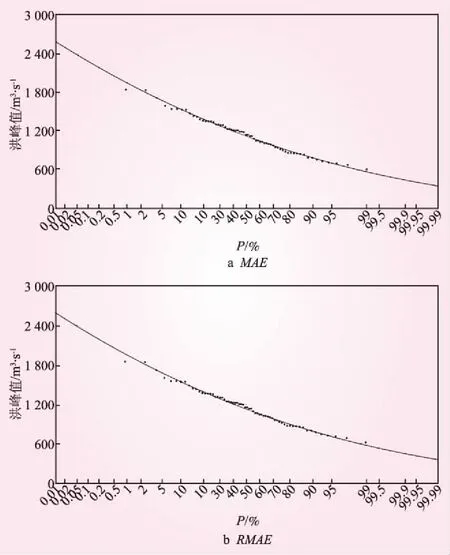
图9 甘孜站洪水频率曲线优化适线成果

图10 甘孜站基于不同目标函数的设计洪水对比示意

由图10可知，采用RMAE为目标函数的NOES方法计算的洪水设计值要比采用MAE为目标函数的NOES方法计算的洪水设计值偏大0.09%～0.18%，其平均值为0.14%；随着频率P的减小，两者的绝对误差逐渐增大。

5 结 论

结合洪水频率分析适线法的计算目的和洪水样本误差规律，构建了一种新的目标函数——平均绝对根误差RMAE，为采用NOES方法计算洪水设计值时合理选取目标函数提供了试验依据，其研究结论如下：

(1)从统计参数值、频率设计值的无偏性和有效性整体上来讲，采用平均绝对根误差RMAE为目标函数的NOES方法整体上精度高且稳健性优良，尤其在设计值无偏性上的优势更为明显。

(2)由于实测洪水样本序列的随机性和复杂性，各个样本点据在目标函数中的作用尚无统一的规律；基于传统水利水电工程水文设计经验，一般设计中考虑大洪水点距具有更大的权重，构建一种随着次序增大权重减小的权函数；或者基于误差规律，考虑大洪水点距具有更大的方差或信息熵，构建一种随着次序增大权重增大的权函数；经统计试验表明，两者均不能有效提高洪水设计值的统计特性，反而会增大洪水设计值的不确定性。