三自由度上肢康复机器人运动学分析和运动轨迹规划仿真*

2020-01-03栾晓燕王金武富灵杰戴尅戎曹岚

生物医学工程研究 2019年4期

栾晓燕，王金武,△，富灵杰，戴尅戎，曹岚

(1.上海交通大学生物医学工程学院，上海 200030；2.上海骨科内植物重点实验室，上海交通大学医学院附属第九人民医院，上海 200011)

1 引言

随着中国老龄化问题的加重，中风患者逐年增加。由中风引起的上肢运动功能障碍患者，在康复期间如果没有接受及时有效的康复训练，会造成关节挛缩，产生无法恢复的运动功能损害[1]。本研究设计了一款上肢康复机器人，具有肩关节的屈/伸，外展/内收以及肘关节的屈/伸三个自由度。康复机器人不同于工业机器人，追求的不是高精度控制和快速响应，而是安全地完成规定的康复运动[2]，因此，需要预先对机器人进行运动学分析和运动轨迹规划仿真，为后续康复机器人的控制提供依据[3]。

2 上肢康复机器人的结构与运动学分析

2.1 上肢康复机器人的结构

本研究设计的上肢康复机器人机械结构见图1，所有的零件均是在UG10.0中设计装配获得，大小臂托盘用来承载和固定患者的大小臂，使上肢随着托盘的运动而运动，并且大臂托盘的长度可以调节，以适应不同患者的臂长。康复机器人辅助患者训练时，患者采取坐姿，为适应不同坐姿身高的患者，利用电机驱动丝杆螺母调节基座高度。康复机器人具有肩关节屈/伸，外展/内收以及肘关节屈/伸三个转动副，转动副的轴线与人体对应关节的转动中心重合，三个转动副的转动依靠电机驱动完成。

图1 上肢康复机器人机械结构图

机器人连杆关系的研究通常采用D-H法。D-H坐标系因为坐标原点设置的不同分为前置D-H坐标系和后置D-H坐标系，有研究表明这两种坐标系是等价的[4]。本研究采用后置D-H坐标系法，建立的机器人各连杆D-H坐标系见图2。

图2 上肢康复机器人各连杆D-H坐标系

为了使设计的上肢康复机器人适合大多数人使用，机器人的连杆长度参照GB10000-88中国健康成年人身体尺寸文件，选择超过95%人群的平均尺寸[1]。因此L1=80 mm,L2=338 mm,L3=258 mm。关节变量q=[θ1θ2θ3]，其中θ1,θ2,θ3分别代表肩关节外展/内收，肩关节屈/伸和肘关节屈/伸的角度。

两相邻连杆间的关系用四个参数表示，分别是关节角θ，连杆偏置d，连杆长度a以及扭角α[5]。本研究设计的三自由上肢康复机器人的连杆参数见表1。

表1 上肢康复机器人的连杆参数

2.2 上肢康复机器人的运动学分析

康复机器人的运动学分析是研究机器人末端位姿与关节角之间的关系，分为正向运动学分析和逆向运动学分析[1]。

相邻连杆i-1和连杆i的位姿关系可以通过相邻连杆坐标系之间的齐次坐标变换矩阵表示[5]。此关系式为：

M(i-1)i=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(x,αi)

(1)

根据表1中的数据，分别可以获得M01,M12,M23。因此机器人末端坐标系相对于基座坐标系的位姿矩阵M03，即运动学方程为：

nx=cθ1×cθ2×cθ3-cθ1×sθ2×sθ3

ny=sθ1×cθ2×cθ3-sθ1×sθ2×sθ3

nz=sθ2×cθ3+cθ2×sθ3

ox=-cθ1×cθ2×sθ3-cθ1×cθ3×sθ2

oy=-cθ2×sθ1×sθ3-cθ3×sθ1×sθ2

oz=-sθ2×sθ3+cθ2×cθ3

(2)

ax=sθ1

ay=-cθ1

az=0

px=L1×cθ1+L2×cθ1×cθ2+L3×cθ1×c(θ2+θ3)

py=L1×sθ1+L2×cθ2×sθ1+L3×sθ1×c(θ2+θ3)

pz=L2×sθ2+L3×s(θ2+θ3)

根据位姿矩阵的定义，机器人末端的姿态和坐标分别为：

(3)

由式(2)可知，正向运动学分析公式明确，计算简单。但逆向运动学分析随着机器人自由度的增加，会出现多组逆解的情况[6]，需要根据特定情况选择最优解。

3 基于matlab的机器人仿真

3.1 机器人建模

利用matlab机器人工具箱Robotics Tool中的Link和SerialLink函数，建立机器人运动学模型。根据表1中的上肢康复机器人的连杆参数，确定函数的输入，具体Matlab程序如下，并将机器人模型命名为My Robot。

L(1)=Link([0,0,0.080,pi/2])

L(2)=Link([0,0,0.338,0])

L(3)=Link([0,0,0.258,0])

r=SerialLink(L,′name′, ′My Robot′);

3.2 三自由度上肢康复机器人的工作空间

康复机器人的工作空间是指机器人末端所能到达的所有空间的集合[7]。正常情况下，人体上肢肩关节和肘关节的运动范围见表2。

表2 人体肩关节和肘关节正常运动范围

利用康复机器人进行辅助康复训练必须保证安全性，所以康复机器人关节的运动范围一定要限制在人体关节正常活动范围之内[8]。本研究设定的三自由度上肢康复机器人的关节运动范围见表3。

表3 肢康复机器人肩关节和肘关节运动范围

根据表3，利用matlab编程，可以获得机器人的工作空间，见图3。后续所有的轨迹规划均需要控制在康复机器人工作空间内。

4 运动轨迹规划仿真

康复机器人的运动轨迹规划分为关节空间轨迹规划和笛卡尔空间轨迹规划两种[7]。关节空间轨迹规划具有规划简单，但无法直观显示机器人末端轨迹的特点。笛卡尔空间轨迹规划具有末端轨迹直观，但易出现特殊关节运动的特点[9]。

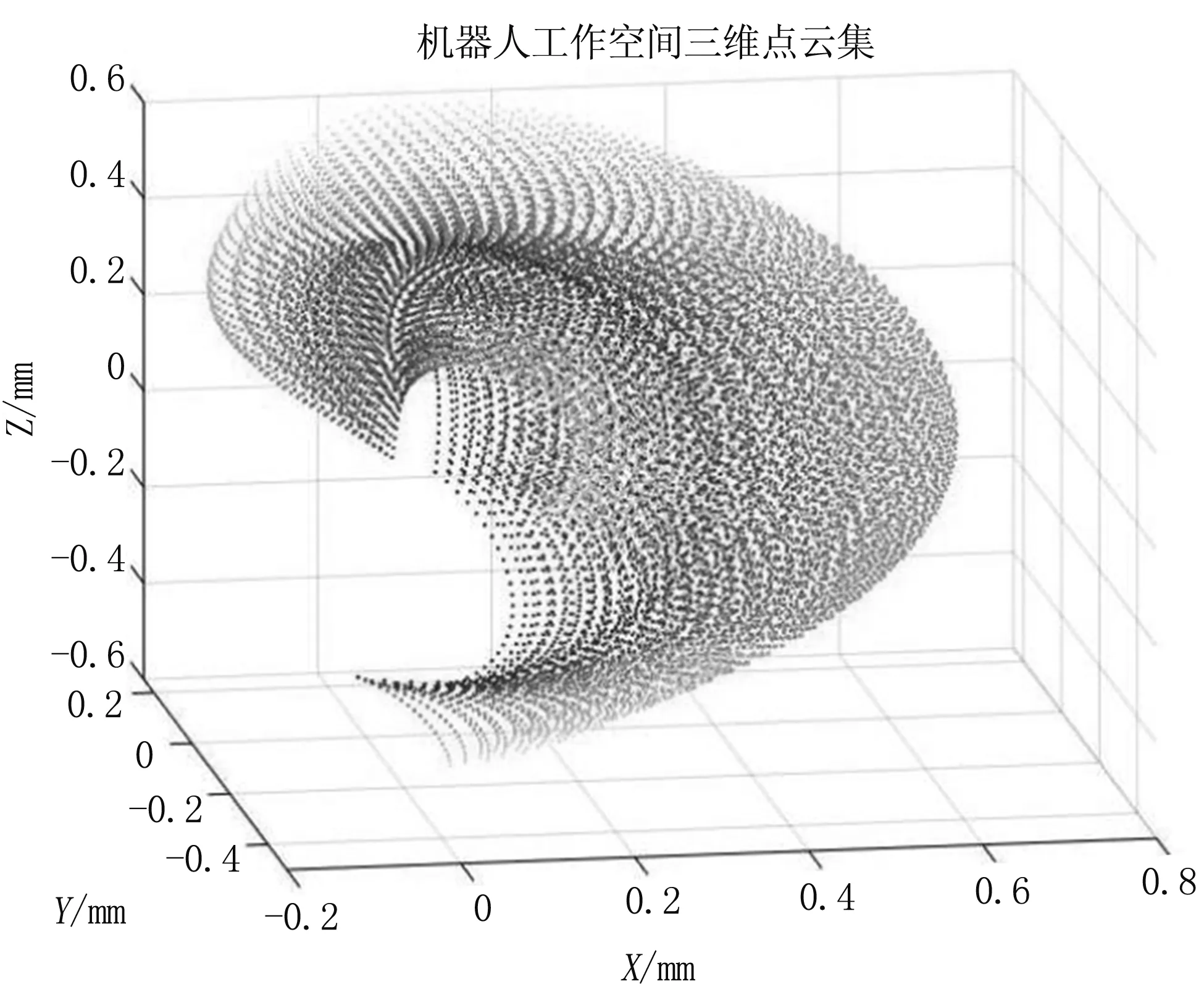
图3 机器人工作空间

4.1 关节空间轨迹规划

根据所设计的三自由度上肢康复机器人，设定起始和终止状态的关节变量分别为q0=[0 0 0]、q1=[pi/6pi/6 2*pi/3]。利用matlab机器人工具箱Robitcs Tool中的轨迹规划函数jtraj，获得规划轨迹见图4。

图4 关节空间运动轨迹图

三个旋转关节随着时间变化的角位移、角速度和角加速度曲线见图5。发现关节角位移连续且角速度和加速度曲线光滑，证明仿真过程中机器人运动平稳，无太大波动。

4.2 笛卡尔空间轨迹规划

利用运动正解函数fkine，解得在关节变量为q0=[0 0 0]、q1=[pi/6pi/6 2*pi/3]时机器人末端位姿分别为t1=transl(0.6760,0,0)、t2=transl(0.1293,0.0746,0.2980)，并以t1，t2作为始末状态进行轨迹规划。利用轨迹规划函数ctraj，获得规划轨迹见图6。