地震作用下双槽渡槽半主动变阻尼控制分析

2020-01-03徐建国王露安崔军豪徐一鸣

水利与建筑工程学报 2020年6期

徐建国，王露安，崔军豪，徐一鸣

(1.郑州大学水利科学与工程学院，河南郑州 450001；2.中建八局华北公司，河南郑州 450001)

由于半主动变阻尼控制在结构振动控制方面起到了很好效果，并在结构抗震减灾中得到了不断应用。半主动变阻尼控制装置通过适时调整结构阻尼来消耗能量，达到降低结构关键部位地震响应的目的。由于仅仅需要调整液压伺服阀的开口大小，故而所需的电能较少[1]，避免了主动控制所需要的高额定电压、能量消耗过大等导致的对系统控制要求过高的缺陷。变阻尼控制属于半主动控制，其控制力较容易实现，并且可以保证控制力出力大及在施加过程中的连续可变的特性。

Mohsen等[2]对半主动电磁摩擦阻尼器进行了全面的研究，并提出一种新的结构形式“SEMFD”。Gkatzogias等[3]通过对半主动控制技术在桥梁工程中的应用，提出一种基于性能的控制原则框架。Zhang等[4]提出一种新型AMD阻尼器件，以抑制不同地震激励下的桥梁振动。Wang等[5]研究了一种振动控制策略，并进行了实验验证。林耿雄[6]以减震榫为例，研究了分离支座在桥梁结构振动控制中的优势。董延东[7]通过对桥梁横向振动控制的研究，证实了桥墩横向刚度对结构振动有较大影响。黄永玖等[8]通过试验研究，表明剪切式高阻尼橡胶减震器对拉索体系具有良好的减震效果。黄劲柏等[9]对高排架预应力混凝土渡槽建立了力学简化模型，分析了三种抗震减震支座的渡槽上部结构自振周期、排架墩地震响应分析、上部结构地震位移响应和上部结构支座剪切变形响应，并对抗震减震效果进行了评价。潘崇仁[10]通过有限元软件建立克孜河渡槽三维模型，模拟渡槽运行期温度、应力分布规律。结果表明：运行期温度应力较大，通过在渡槽外壁采取保温措施，有效的改善了槽身的应力状态。张威等[11]基于混凝土连续介质损伤力学和概率密度演化理论，结合物理随机地震动建模方法和精细化有限元分析程序，建立了大型渡槽结构随机动力反应分析与可靠度评估框架。汪权[12]针对地震作用下高层结构振动调谐质量阻尼器(TMD)被动控制问题，基于沿结构高度分布多个阻尼器的策略，研究分布式多重调谐质量阻尼器(DMTMD)控制策略并应用于高层结构振动控制中。邬家利[13]拆解阻尼器观察其内部变化情况，发现磁流变液泄漏或沉淀; 对阻尼器密封性能进行了实验，得到了不同安装角度的泄漏情况。张玉民[14]研究了渡槽结构伸缩缝两端在地震中可能发生碰撞现象，危害渡槽的安全运营，甚至导致落梁破坏，针对这一问题，通过建立考虑碰撞效应的渡槽动力分析模型，研究了碰撞效应对渡槽地震反应的影响，并提出了对渡槽减震半主动控制方法。

鉴于半主动变阻尼装置在实际工程减震防灾领域的不断应用，且由于其在大型渡槽结构振动控制的研究较少，故此开展大型双槽渡槽地震响应振动控制研究很有必要。

1 双槽渡槽半主动变阻尼控制分析模型

1.1 双槽渡槽薄壁结构弹塑性动力分析模型

本文采用双槽渡槽梁段单元非线性动力分析模型，计算渡槽结构横向地震减震控制计算[15](双槽渡槽截面示意图见图1)。双槽渡槽截面尺寸较大，不能按照一般的开口薄壁梁来分析计算。通常做法是根据渡槽底板横向连接较为薄弱的结构特点，在每个渡槽底板中点处假想断开，将渡槽截面化为多个刚性横截面(不计渡槽底板变形)的简单薄壁梁(见图2)，各自沿其形心C弯曲，并绕其扭心S扭转。双槽渡槽非线性模型集渡槽线弹性模型与非线性多弹簧模型为一体，并应用多弹簧等效关系模拟结构塑性铰区的非线性滞回特性，充分考虑了截面混凝土、普通钢筋和预应力钢筋对非线性弹簧滞回曲线特征参数的影响，较全面准确地反映了结构的非线性动力性能。

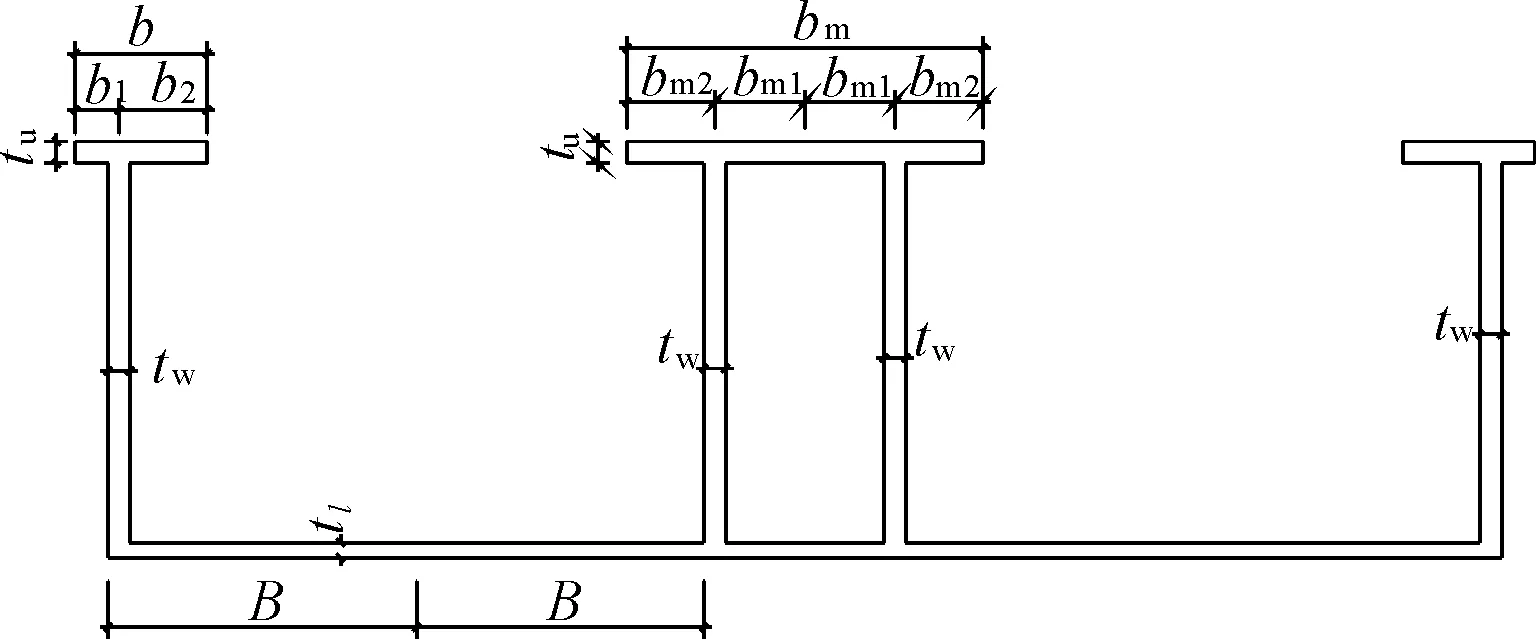
图1 双槽渡槽横截面

图2 横截面划分示意图

当渡槽截面在受到双向弯矩发生弯曲变形时，则此时的截面弯曲变形的中性轴并不与截面惯性主轴平行，这就要求进行微元划分和求解截面内力时必须沿主轴双向划分单元。应变计算时按照平截面假设，设某一位置处等效非线性弹簧内力和轴向变形可求为：

(1)

(2)

(3)

(4)

式中：Ps、δs分别表示某非线性弹簧的内力和单位长度的轴向变形；xs、ys为该非线性弹簧的位置坐标；φx、φy分别表示横截面对x轴和y轴的转动曲率[15]。

按照Guyan静力凝聚的方法，将多弹簧弹塑性渡槽薄壁结构单元模型与渡槽弹性模型整理组合为一体。分别采用能量驻值原理和虚位移原理建立空间双槽渡槽非线性动力分析模型(见图3)[9]。

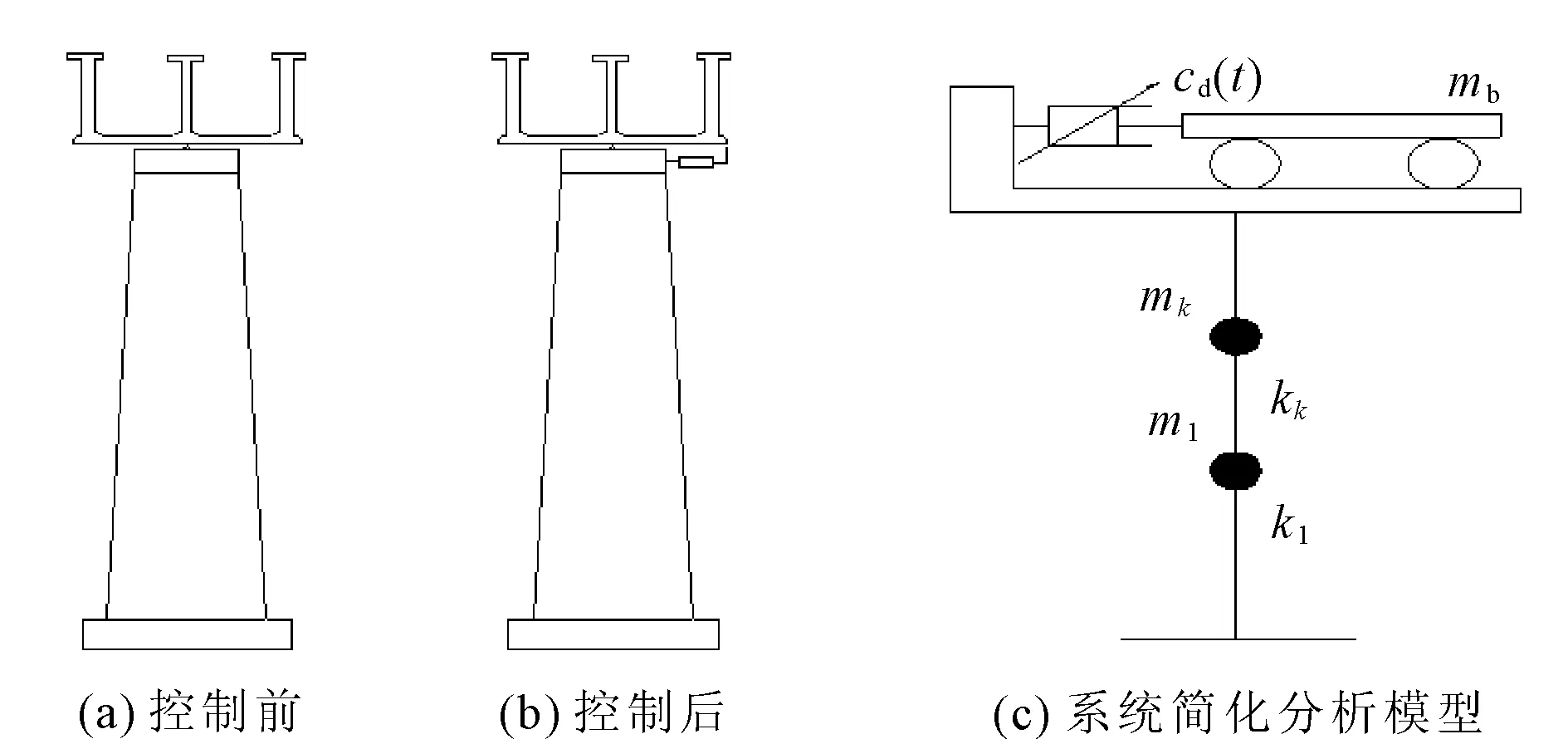
图3 双槽渡槽半主动结构控制系统

双槽渡槽结构层间剪切模型在安装变阻尼控制器装置后的动力方程：

(5)

整体阻尼阵采用Rayleigh阻尼：

C=aM+bM

(6)

其中：

原方程经整理后得：

(7)

其中：

式中：mb为双槽渡槽上部结构质量；kb为橡胶支座的水平刚度；cd(t)为阻尼器滞变系数。

1.2 变阻尼器控制原理

变阻尼控制器由调孔阀、液压缸及输油管线几部分组成(见图4)，当渡槽结构在地震荷载作用下产生动力响应时，测试系统自动检测到结构响应参数，由处理系统计算出相应阻尼力大小，并反馈控制系统作为调节孔阀开口尺寸的依据，从而实现变阻尼控制实施。当调孔阀完全关闭时，提供的阻尼力最大；当旁路调孔阀完全打开时，阻尼力最小。通过控制器连续调整管路上孔径的开口大小，使得阻尼器的阻尼系数在[Cdmin，Cdmax]区间连续变化，从而实现对变阻尼器的控制。

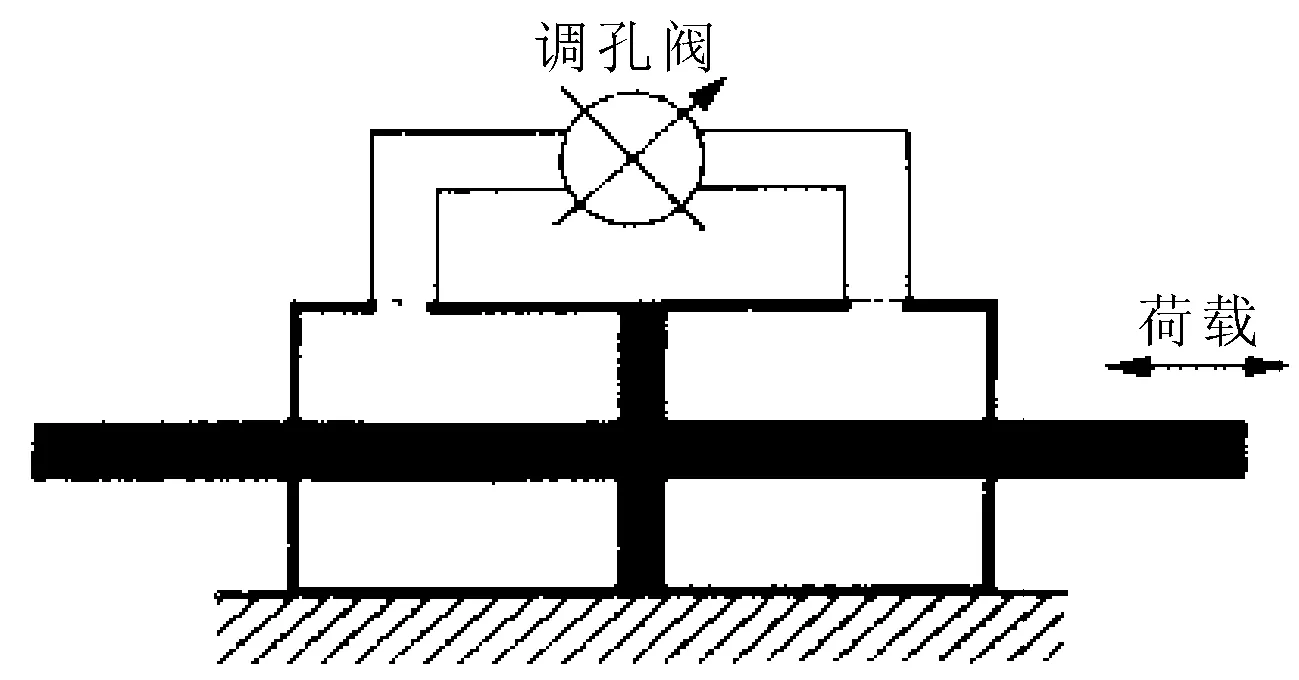
图4 变阻尼作动器示意图

1.3 控制装置的计算模型

模型主要建立了阻尼控制器装置中关于控制阻尼力、动力响应量和输入电压之间的函数关系。变阻尼作动器所提供的阻尼力由Maxwell模型确定：

(8)

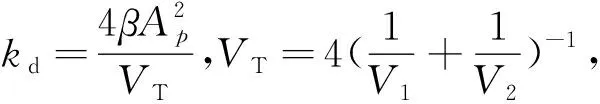
对于变阻尼控制器阻尼力计算模型，其它参数仅与变阻尼控制装置的固有参数和缸内流体特性有关，只有阻尼系数cd可以通过控制调孔阀的开口大小调节，并且可以近似表示为：

cd=(1-λ)cdmin+λcdmax

(9)

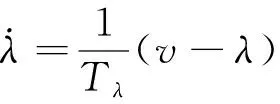
式中：cdmin和cdmax分别为变阻尼器所能提供的阻尼系数上下限值；λ为调孔阀开口控制参数，其取值范围为0≤λ≤1，Tλ为时间常数，v为控制电压。

2 主动控制力计算

(10)

Z(0)=0

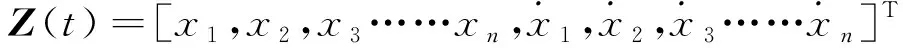
对于LQR算法，其性能指标定义为：

(11)

式中：tg为地震持续时间；Q2n×2n，Rp×p加权系数矩阵。

由式(4)、式(5)得到最小的主动控制力向量U(t)：

U(t)=-R-1BTPZ(t)

(12)

即：U(t)=-GZ，G称为增益矩阵

P由下式求解得到：

-PA-ATP+PBR-1B-TP-Q=0

3 半主动变阻尼控制力计算

采用离复位控制算法为控制策略，即通过适时采集作动器瞬时速度，权衡控制力与结构运动关系来确定具体取值大小。根据控制阻尼力与可调控制阻尼之间的换算关系，采用限界Hrovat控制算法调整变阻尼控制力。

(13)

4 计算实例

双洎河渡槽是南水北调中线总干渠最大的渡槽之一，渡槽全长240 m，单跨跨度40 m，全槽共分为1～6号跨，槽墩分为1～5号墩，在每个槽墩与槽身之间安装有可变阻尼器，槽身为预应力钢筋混凝土结构，渡槽与槽墩支墩的连接方式为简支，双槽槽身采用矩形单隔墙型式，槽身及墩体尺寸见图5、图6。槽身采用C50混凝土，槽墩采用C30混凝土，盆式橡胶支座弹簧水平向刚度为3.0×109N/m，槽墩底部采用钻孔灌注桩基础，现简化为固定端约束模式。渡槽槽身和支墩均采用考虑塑性铰的弹塑性梁段单元模型，该模型分为弹性梁段单元和非线性弹簧单元两部分，其中非线性弹簧单元按照其非线性加卸载曲线分析计算。渡槽结构阻尼采用瑞利阻尼，阻尼比ζ为0.05，a=0.256，b=0.008；地震荷载采用调幅0.2g的El Centro、Taft和Tianjin地震波；可变阻尼器的阻尼系数cd(t)下限为989.60 kN·s/m，上限为54 889.30 kN·s/m。

从El Centro波减震控制效果来看(见图7—图16)，第1跨跨中位移主动与半主动控制效率分别为75%和40%；第2跨跨中位移主动与半主动控制效率分别为71%和39%；第3跨跨中位移主动与半主动控制效率分别为75%和40%；1号墩墩顶位移主动与半主动控制效率分别为75%和40%；2号墩墩顶位移主动与半主动控制效率分别为37%和7%；第1跨跨中加速度主动与半主动控制效率分别为36%和10%；第2跨跨中加速度主动与半主动控制效率分别为7%和4%；第3跨跨中加速度主动与半主动控制效率分别为36%和2%；1号墩墩顶加速度主动与半主动控制效率分别为10%和0.4%；2号墩墩顶加速度主动与半主动控制效率分别为10%和2%；3号墩墩顶加速度主动与半主动控制效率分别为23%和5%；3号墩半主动控制作动器最大出力占主动控制作动器的34%。

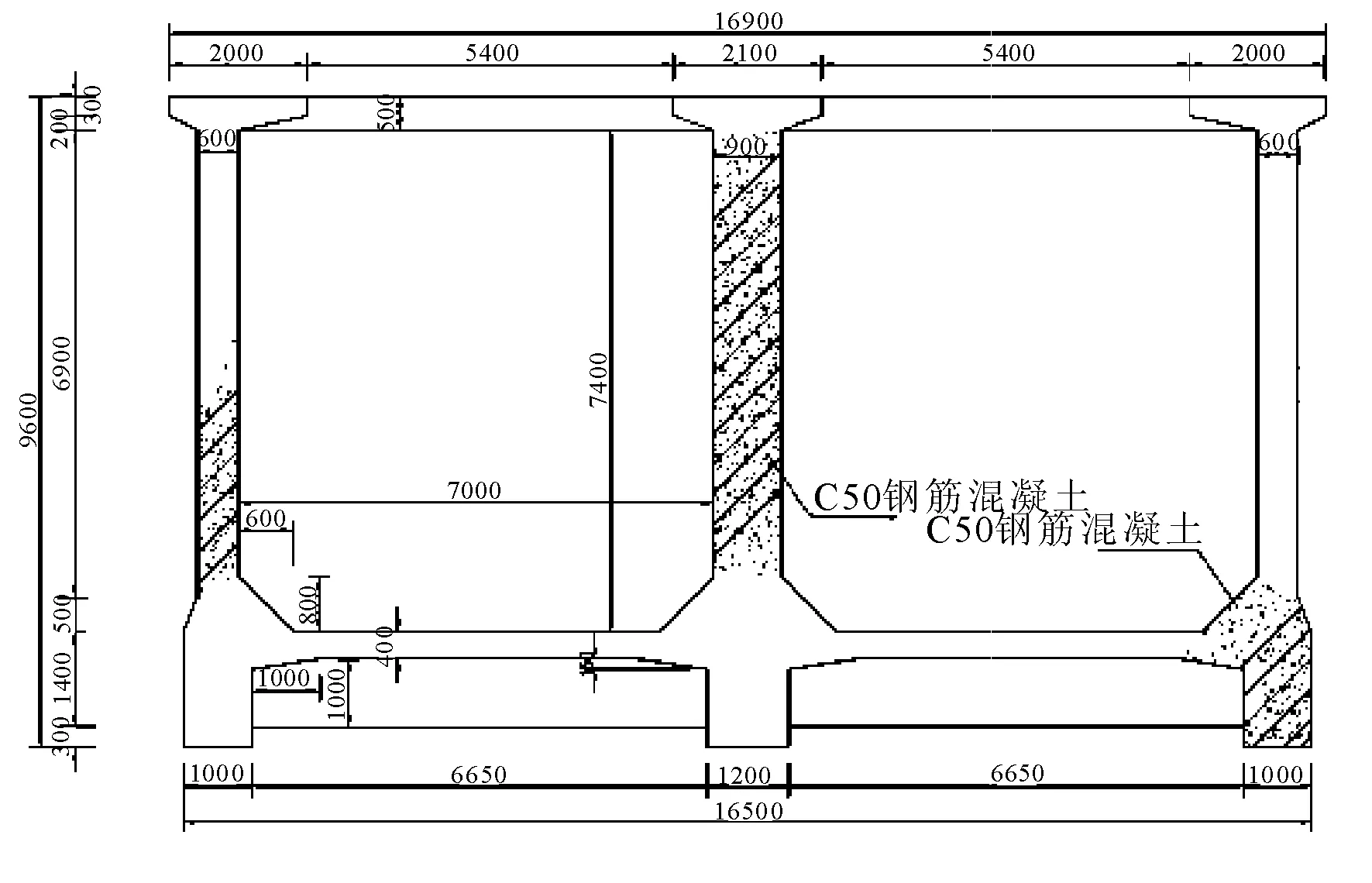
图5 双槽渡槽横截面示意(单位：mm)

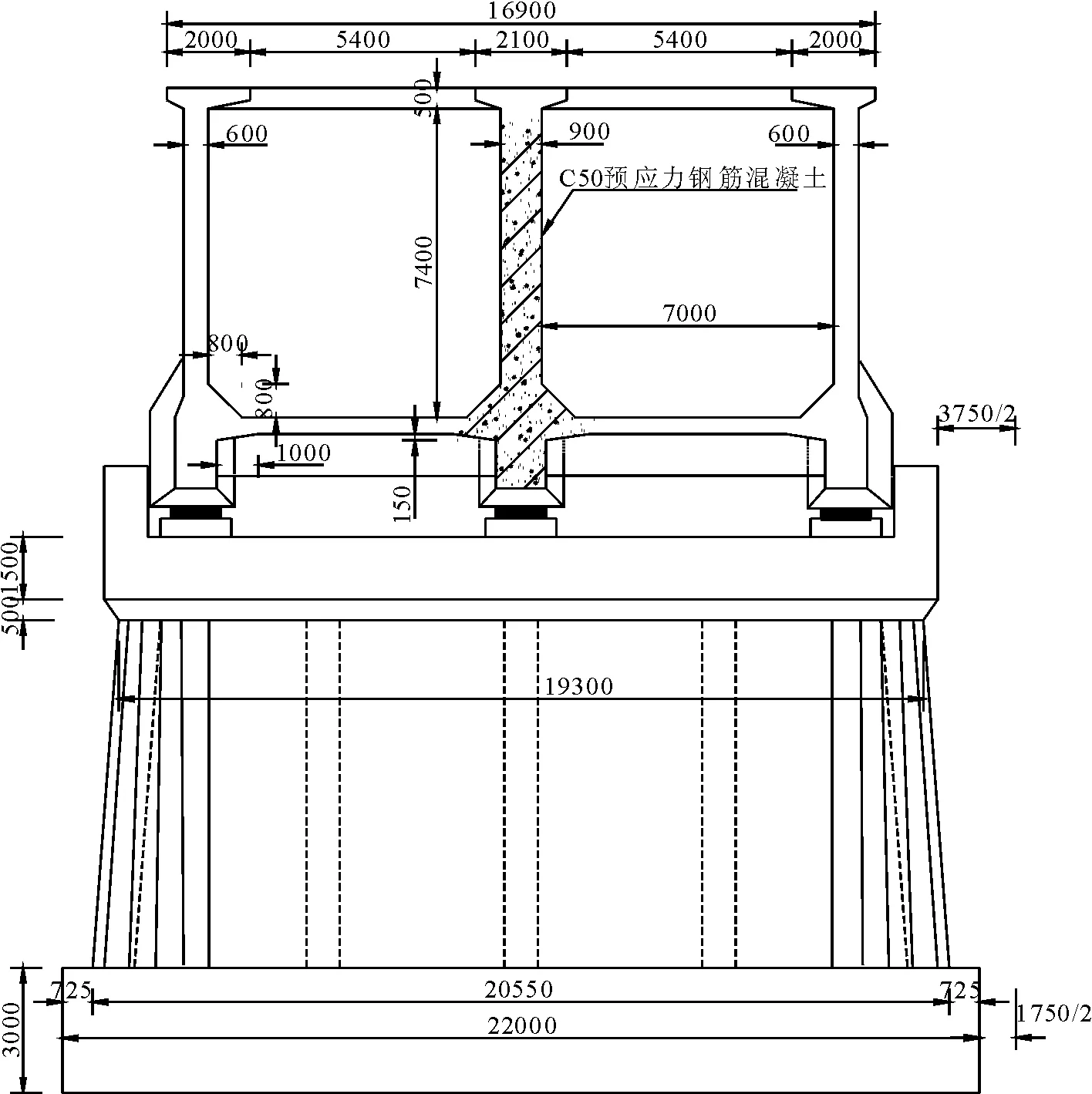
图6 渡槽横断面及槽墩尺寸示意(单位：mm)

从Taft波减震控制效果来看(见图17—图20)，第1跨跨中位移主动与半主动控制效率分别为86%和52%；第2跨跨中位移主动与半主动控制效率分别为87%和52%；第3跨跨中位移主动与半主动控制效率分别为69%和48%；1号墩墩顶位移主动与半主动控制效率分别为75%和50%；2号墩墩顶位移主动与半主动控制效率分别为58%和17%；第1跨跨中加速度主动与半主动控制效率分别为61%和15%；第2跨跨中加速度主动与半主动控制效率分别为60%和10%；第3跨跨中加速度主动与半主动控制效率分别为61%和15%；1号墩墩顶加速度主动与半主动控制效率分别为47%和7%；2号墩墩顶加速度主动与半主动控制效率分别为10%和2%；3号墩墩顶加速度主动与半主动控制效率分别为15%和0.02%。

图7 El Centro波第1跨跨中位移比较

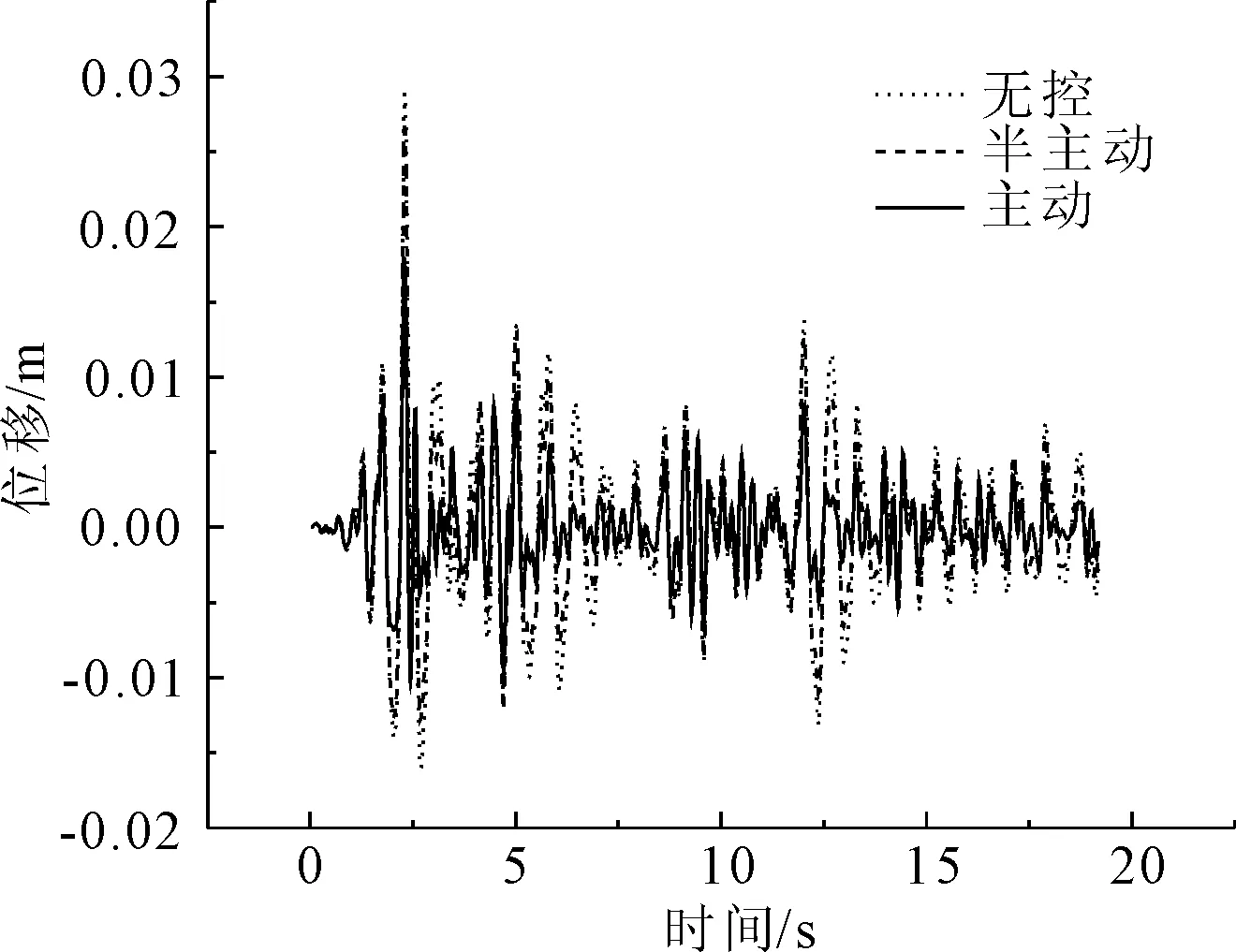
图8 El Centro波第3跨跨中位移比较

图9 El Centro波2号墩顶位移比较

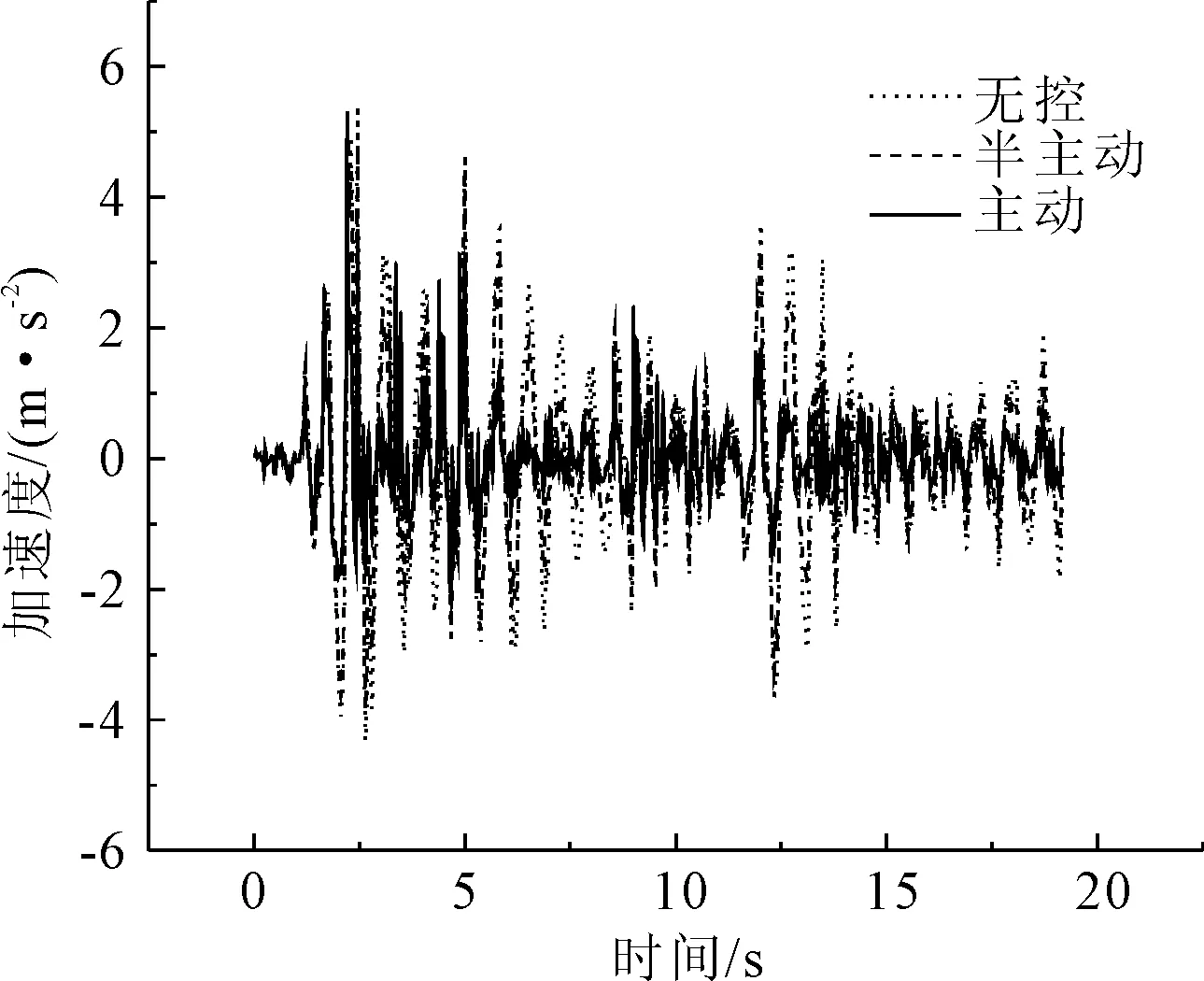
图10 El Centro波第1跨跨中加速度比较

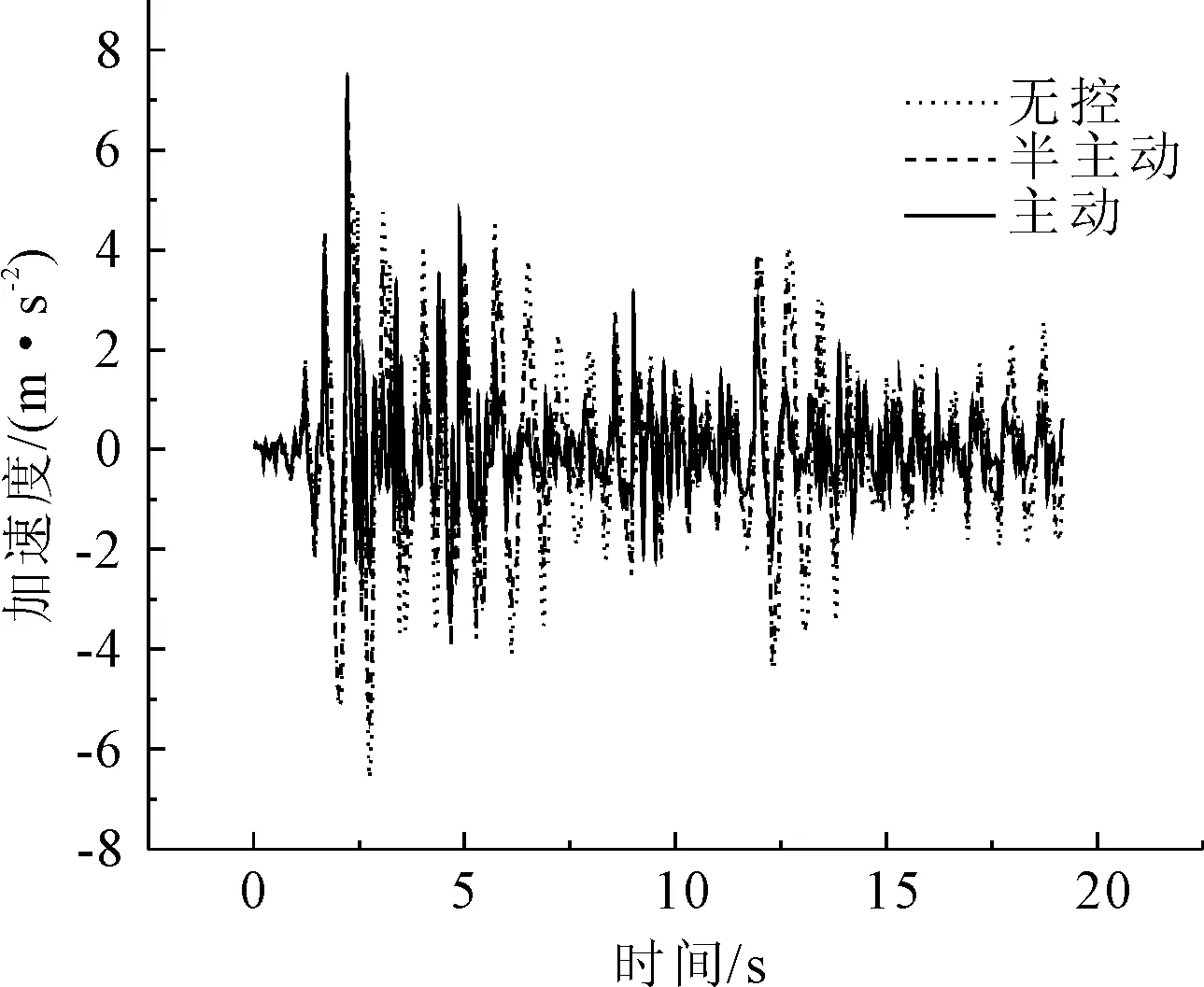
图11 El Centro波第2跨跨中加速度比较

图12 El Centro波第3跨跨中加速度比较

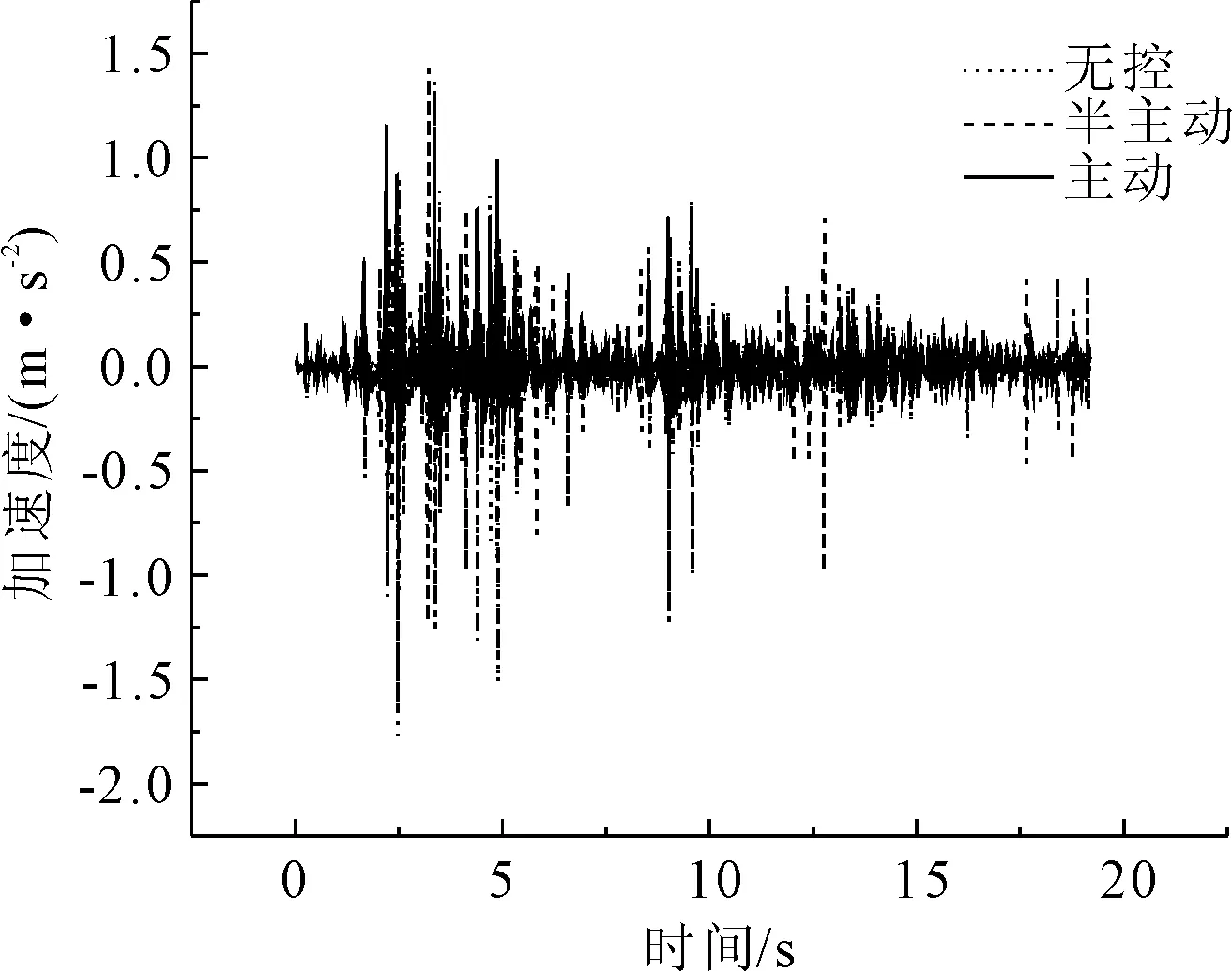
图13 El Centro波1号墩顶加速度比较

图14 El Centro波2号墩顶加速度比较

图15 El Centro波3号墩顶加速度比较

图16 El Centro波3号墩控制器控制力比较

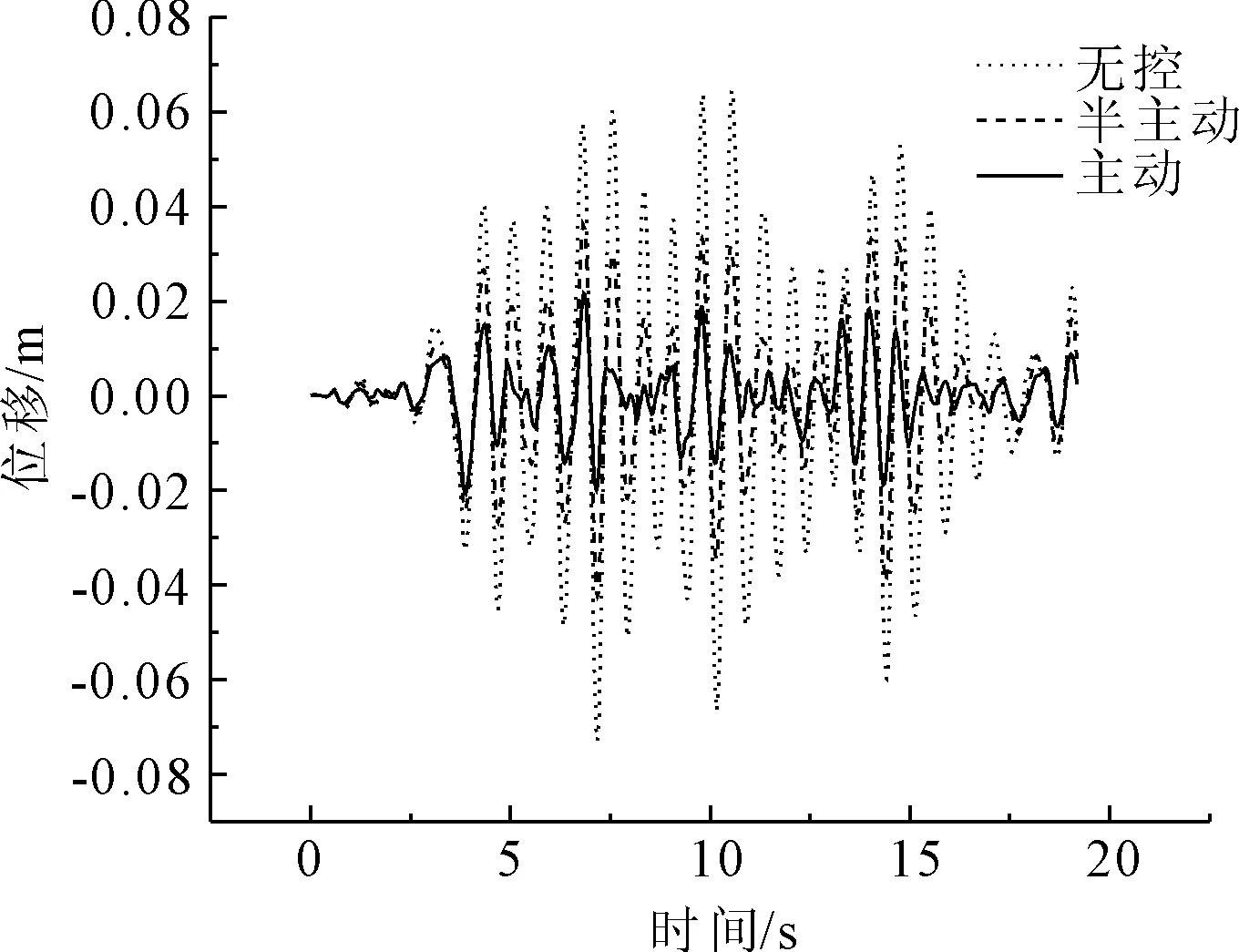
图17 Taft波第1跨跨中位移比较

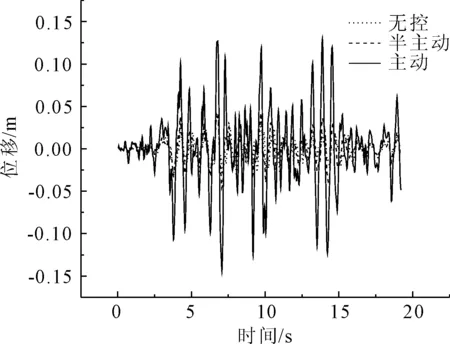
图18 Taft波1号墩顶位移比较

从Tianjin波减震控制效果来看(见图21—图24)，第1跨跨中位移主动与半主动控制效率分别为70%和38%；第2跨跨中位移主动与半主动控制效率分别为67%和39%；第3跨跨中位移主动与半

图19 Taft波2号墩顶位移比较

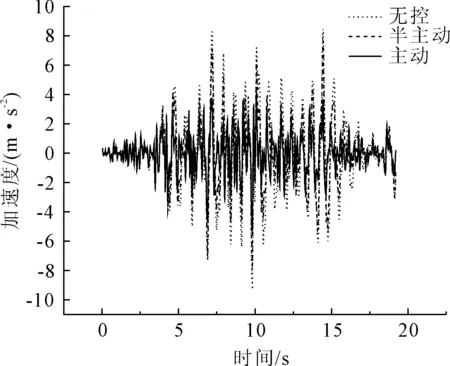
图20 Taft波第2跨跨中加速度比较

主动控制效率分别为70%和39%；1号墩墩顶位移主动与半主动控制效率分别为63%和50%；2号墩墩顶位移主动与半主动控制效率分别为63%和1%；第1跨跨中加速度主动与半主动控制效率分别为74%和24%；第2跨跨中加速度主动与半主动控制效率分别为67%和22%；第3跨跨中加速度主动与半主动控制效率分别为71%和23%；1号墩墩顶加速度主动与半主动控制效率分别为56%和18%；2号墩墩顶加速度主动与半主动控制效率分别为10%和4%；3号墩墩顶加速度主动与半主动控制效率分别为32%和11%；Taft波1号墩底弯矩值主动与半主动控制分别是无控墩底弯矩值的1.27倍和1.12倍；Tianjin波2号墩底剪力值主动与半主动控制分别是无控墩底剪力值的1.16倍和0.98倍。

图21 Tianjin波第1跨跨中位移比较

图22 Tianjin波第3跨跨中加速度比较

图23 Tianjin波1号墩墩底弯矩比较

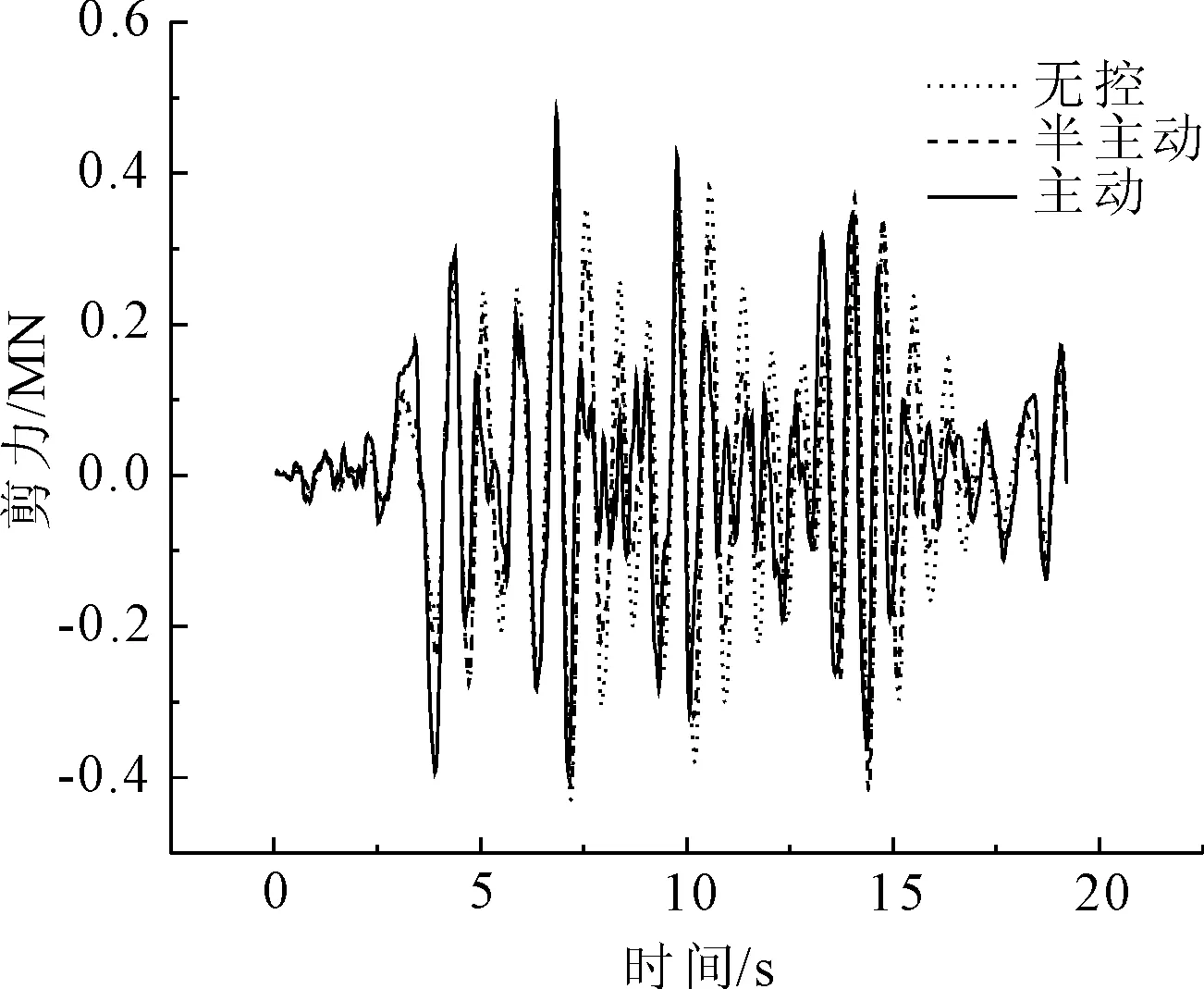
图24 Taft波2号墩墩底剪力比较

从图7—图24地震时程响应曲线，以及表格1—表格3各条地震波下的地震响应对比结果可以看出，主动控制和半主动控制措施都明显降低了各跨跨中横向位移和横向加速度最大值(如El Centro波第三跨跨中横向位移：无控为0.108 m、半主动控制为0.064 m、主动控制为0.027 m；Taft波第二跨跨中横向加速度：无控为8.476 m/s2、半主动控制为7.603 m/s2、主动控制为3.428 m/s2)；对比双槽渡槽槽墩基底总剪力和总弯矩最大值，半主动控制内力较主动控制内力有明显的降低(如Taft波1号墩底剪力：半主动控制为2.18×105N、主动控制为3.87×105N；Tianjin波1号墩底弯矩：半主动控制为3.42×106Nm、主动控制为3.85×106Nm)。同时也可以看到在半主动控制措施施加控制力后，在降低了结构位移反应的同时，部分槽墩墩顶加速度反应有所放大(如Tianjin波第三号墩顶加速度：无控为0.104 m/s2、半主动控制为0.115 m/s2、主动控制为0.071 m/s2)，墩底弯矩和剪力较无控时也增大明显，这主要是由于控制力反向施加于槽墩顶部造成的影响。同时也可以看出，半主动变阻尼控制效果对关键部位的位移控制优于对加速度的控制；半主动变阻尼控制作为被动控制装置，即使当外部大功率电源供电中断时也可以保持较好的控制效果。