植物网纹增厚导管流体力学建模与流动特性分析

2020-01-03徐天宇张立翔

排灌机械工程学报 2020年1期

徐天宇，张立翔

(昆明理工大学建筑工程学院，云南昆明 650500)

水分对于植物的生理生态有着重要的作用,它直接或间接影响着植物生长发育过程中的各种生理活动[1].木质部是连接根系和冠层的主要输水通道，水分由根系通过木质部到达叶片部，而输送的通道就是分布在木质部内部的导管和管胞[2].导管和管胞长短不一，内径一般为微米量级[3-5]，管内组织结构凸凹不均，分布较为复杂，导致导管水分传输的计算较为困难，目前仍以试验观测为主要手段[6-7].

为弥补试验观测的不足，一些学者采用CFD的方法构建木质部导管输水模型，探索导管流动特性.如ROTH[8]建立了导管二维简化模型，分析环纹导管的流动特性，得出水分流动特性与环纹间距的关系.徐天宇等[9]建立植物单管胞阻力计算的数学模型，研究纹孔结构与植物管胞内径及电阻率的关系，得出纹孔深度、纹孔直径、纹孔塞直径是影响管胞电阻率的主要因素.陈琦等[10]使用低雷诺数k-ε模型对管胞具缘纹孔进行数值模拟，发现纹孔的压降与纹孔塞直径成正比，与纹孔直径、纹孔深度成反比.大多数研究是对导管环纹、穿孔板和管胞纹孔的建模分析，而木质部导管成熟后的二次生长阶段会产生环纹、螺纹、网纹和孔纹等不同形式的次生加厚[11]，不同导管增厚形式对水分输运不尽相同，体现木质部输水方式的多样性，其中陈琦等[12]使用SSTk-ε模型对导管内壁环纹和螺纹增厚流动进行了数值模拟，而木质部导管成熟后期，木质部导管会产生更加复杂的网纹增厚[13]，其增厚方式对水分输运的影响研究鲜见报道.

文中提出一种网纹螺旋线数量分布模型，模拟木质导管网纹增厚对水分输运的影响.结合伯努利方程和层流模型的数值模拟，通过等效阻力系数的变化，分析导管内壁网纹螺旋线数量、螺纹间距、网纹高度、网纹宽度等因素对导管内部微流动的影响，揭示植物生长过程中通过木质部导管增厚的机制对导管水分输送的控制机理.

1 内壁网纹增厚导管模型

1.1 增厚导管模型

植物木质部导管内壁二次生长的增厚形式如图1所示.图1c,d显示了从网纹增厚到孔纹增厚的过渡过程，而孔纹增厚后期会产生联通两导管的纹孔结构，其中内壁网纹增厚是木质部二次增厚的一个常见的典型结构，也是水分输运的重要途径[11]，因此，文中通过对网纹增厚模型进行建模，探究其对水分输运的影响.

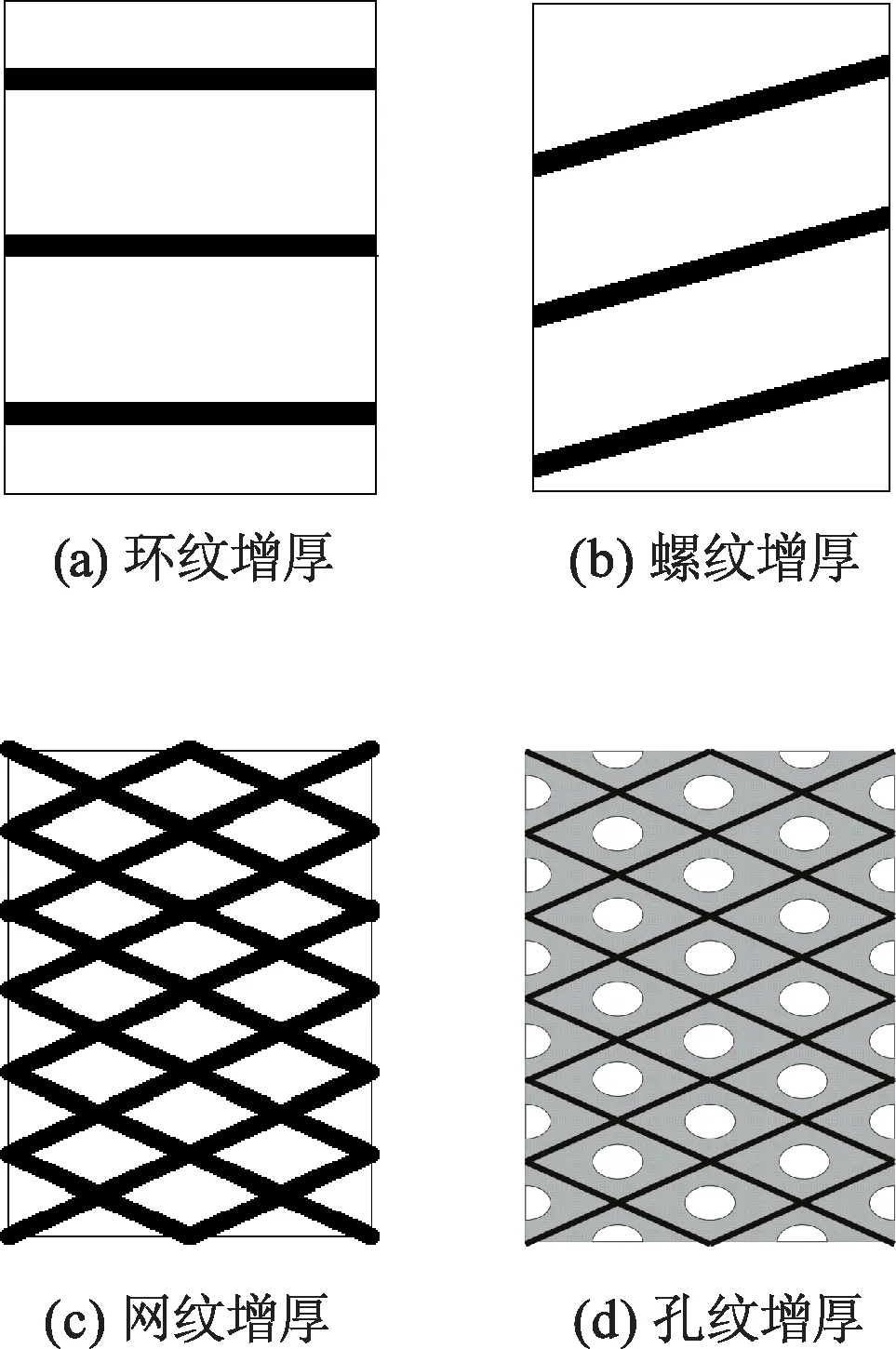
图1 木质部二次增厚示意图

1.2 内壁网纹增厚模型

设植物木质部导管内壁网纹增厚可用具有不同数量且具有一定尺度大小的螺旋线建模，如图2所示.图3为内壁网纹增厚模型沿内壁分布的剖面示意，其中箭头代表水分运动方向；Z1，Z2，…，Zn分别表示断面1、断面2，…，断面n.从图中可以看出，液体进入截面凸部断面2时，由于壁面网纹增厚导致断面收缩，形成进口收缩流，同时也造成凸部出口断面扩散流.由于凸部产生的收缩-扩散流增加流体与壁面的摩擦和碰撞，产生较大的局部能量损失.

图2 内壁网纹增厚导管模型

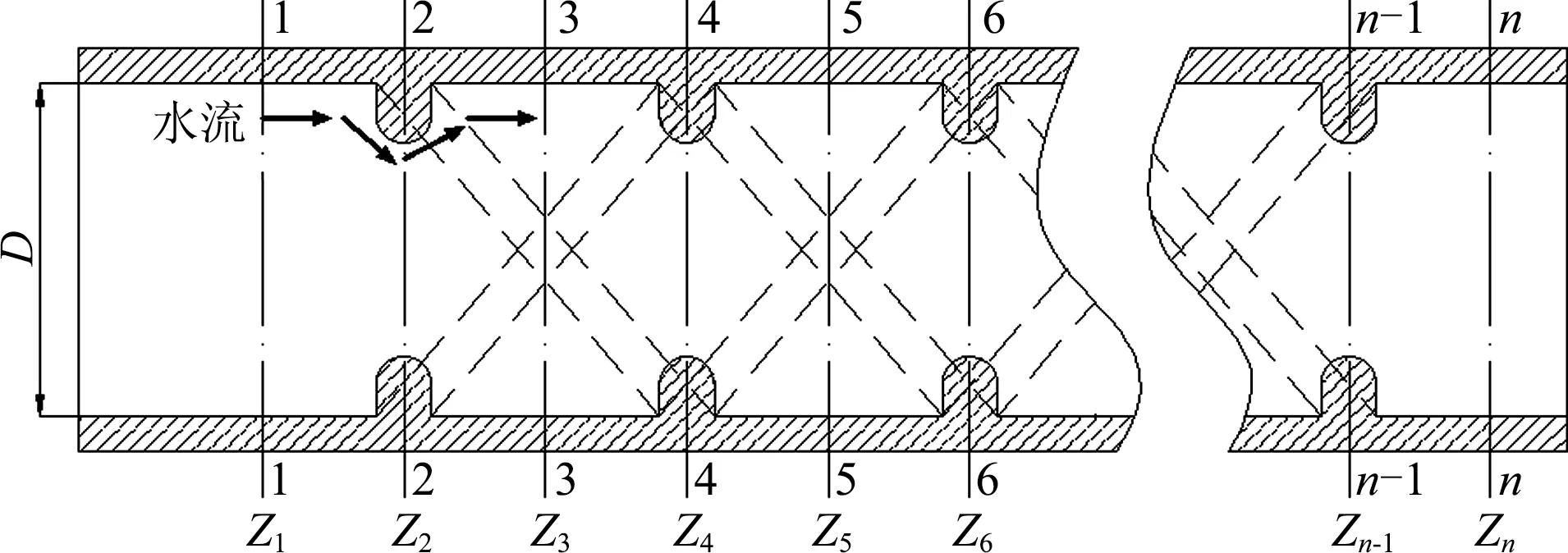
图3 内壁网纹增厚模型的流动示意

Fig.3 Diagram of flow path in reticulated thickening model

假设任意断面间的流动满足伯努利方程，则从进口至出口各断面z1，z2，…，zn间分段写出伯努利方程为

(1)

式中:pn,vn分别为断面n处的平均压力和流速;ρ为液体质量密度;g为重力加速度;zn为断面处的位置水头;ξn-1为断面n-1到断面n的局部损失系数;λ为沿程损失系数;ln-1为相邻两断面间的长度.将式(1)各式等号两边各项依次相加得

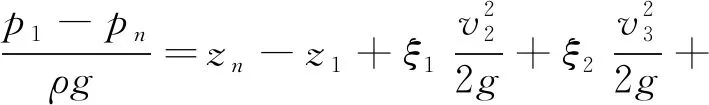
(2)

由导管的连续性方程知

v1A1=v2A2=v3A3=…=vnAn,

(3)

式中:Ai(i=1,2,…,n)为相应断面处的通流面积.将式(3)代入式(2)得

(4)

若令，

(5)

式(4)简化为

(6)

可表示为

(7)

或用流量表示为

(8)

式中:ξ称为导管的等效损失系数;Δp为导管进口至出口的压力差;L=zn-z1为导管长度(垂直高度);Q为导管内平均流量.显然，ξ反映了导管内部网纹增厚及几何特性对流动的影响，而式(7)-(8)则反映了植物导管几何特性、水分输送力以及输送驱动力之间的物理力学关系，揭示了植物导管水分的输送机理.

2 CFD数值模拟

2.1 控制方程

为了确定网纹增厚导管的等效损失系数ξ，在已知边界条件的情况下，还需确定导管计算段进出口间的压差Δp.鉴于管内壁凸点的复杂性，文中采用CFD数值模拟的方法确定Δp.因导管内Re数小于1，根据文献[14-15]的报道，使用层流模型进行结果对比具有更好的计算精度.

2.2 网格设计

考虑到网纹增厚凸部结构的不规整性，网格划分使用四面体或六面体的非结构网格.在凸部突出的区域，由于几何曲率变化较大，在凸部采用网格加密的方式进行细化.网格规模以出/入口压降预测精度为依据，进行网格无关性检验(见表1)，表中N为网格数量，PDD为压降差异,标准网格和细化网格的网格密度计算预测的压降差异为0.24%，认为网格数对计算结果已没有影响，因此采用标准网格密度，其总单元数为724 230个.网纹壁面网格分布形式如图4所示.

表1 网格密度无关性检验

图4 网纹壁面网格分布

2.3 边界条件

当前，木质部导管水分运动的力学机理尚不完全清楚，文中仍按流体力学的基本原理设定水分运动的边界条件.壁面采用非滑移条件，进口已知速度取为0.003 m/s[5]，压力出口为环境气压.同时，为减缓入口、出口人为边界的影响，在进口和出口段设置足够长的计算过渡段.

2.4 数值实现

计算硬件平台为高性能计算系统，使用5台PowerCube-S01云立方汉柏高性能并行计算机，计算软件为ANSYS FLUENT17.1.通过数值模拟计算出不同条件下导管段的压降Δp，再利用式(7)计算导管的等效损失系数，并分析网纹增厚导管内部的流动特性.

3 计算结果

为便于比较分析，取导管网纹模型长度为300 μm，内径为30 μm，纹宽和纹高为4 μm，轴向纹间距为20 μm，螺旋线数量为4，分别对不同导管模型进行计算，分析导管的流动特性.

3.1 凸点分布特性的影响

3.1.1 网纹螺旋线数量

在其他参数设定的情况下，改变导管网纹螺旋线数量，通过CFD数值模拟，可得到导管内部的压力、流速等流场参数，由此可得到导管进/出口压力差Δp、导管流量Q等流动参数，再根据式(7)即可算出网纹增厚导管的等效损失系数ξ如表2所示,表中N1为网纹螺旋线数量，Qa为平均流量，ξ为等效损失系数.

由表2可知，随网纹螺旋线数量增加，网纹导管内平均流量减小，总压降增大，等效损失系数也逐渐增大，当网纹螺旋线数量增加到8条时，压降增大约16.34%，等效损失系数增大约26.45%.这表明，随着网纹螺旋线数量增加，网纹导管中的过流面积减小，平均流量减小，而网纹螺旋线数量增加同时会导致导管内壁的阻力增大，因此导管内的压降增大，等效损失系数随之增大.显然，随螺旋线数量的增加，导管的输送阻力明显加大，输送能力将降低.

表2 导管内网纹螺旋线数量对压降和等效损失系数的影响

Tab.2 Effects of number of helical curls on pressure drop and flow resistance coefficient

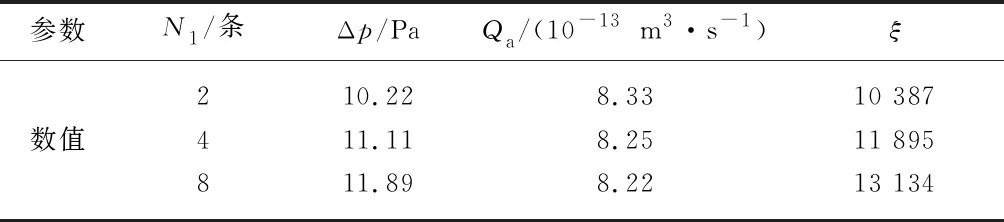
参数N1/条Δp/PaQa/(10-13m3·s-1)ξ210.228.3310 387数值411.118.2511 895811.898.2213 134

3.1.2 导管内径

在其他参数设定的情况下，等效损失系数的计算方法相同，结果见表3，表中lv为导管内径.

表3 导管内径对压降和等效损失系数的影响

Tab.3 Effects of vessel inner diameter on pressure drop and flow resistance coefficient

参数lv/μmΔp/PaQa/(10-13m3·s-1)ξ3011.118.2511 895数值406.0314.854 335503.6723.29951

由表3可知，随导管内径增加，网纹导管内平均流量增大，总压降减少，等效损失系数也逐渐减小，当导管内径增加到50 μm时，压降减少了约66.97%，等效损失系数减少约92.01%.这表明，随着导管内径增加，网纹导管中的过流面积增大，平均流量增大，而网纹螺旋线数量、网纹高度、网纹宽度等导管内壁的阻力参数不变，因此导管内的压降降低，等效损失系数随之降低，输送能力提高.

3.1.3 螺纹间距

在其他参数设定的情况下，等效损失系数的计算方法相同，结果见表4,表中ds为螺纹间距.

表4 导管内螺纹间距对压降和等效损失系数的影响

Tab.4 Effect of helical curl spacing on pressure drop and flow resistance coefficient

数值ds /μmΔp/PaQa/(10-13m3·s-1)ξ1011.658.2212 780数值2011.118.2511 8952511.018.3311 524

由表4可知，随导管内螺纹间距增加，网纹导管内平均流量增加，总压降减小，等效损失系数也逐渐减小，当导管内螺纹间距增加到25μm时，压降减少约5.49%，等效损失系数减少约9.83%.这表明，螺纹间距的增大，使网纹导管内部网纹螺旋线旋转圈数减少，内部总体阻力减少且网纹增厚过流面积增大，压降减少，等效损失系数降低，输送能力提高.

3.1.4 网纹高度

在其他参数设定的情况下，等效损失系数的计算方法相同,结果见表5，表中hv为网纹高度.

表5 导管内网纹高度对压降和等效损失系数的影响

Tab.5 Effects of reticulated curl height on pressure drop and flow resistance coefficient

参数hv/μmΔp/PaQa/(10-13m3·s-1)ξ2.39.538.449 151数值3.010.028.3210 2964.011.118.2511 8955.012.768.2114 455

由表5可知，随导管内网纹高度增加，网纹导管内平均流量减小，总压降增大，等效损失系数也逐渐增大，当导管内网纹高度增加到5.0 μm时，压降增大约33.89%，等效损失系数增大约57.96%.这表明，随着导管网纹高度增加，网纹增厚处的截面面积变小，导致木质部导管的整体流动通道变小，平均流量减少，木质部导管的局部流动阻碍的变大，产生更多的能量损失，从而使得导管压降增加，等效损失系数增大，输送能力降低.

3.1.5 网纹宽度

在其他参数设定的情况下，等效损失系数的计算方法相同.结果见表6，表中bv为网纹宽度.

表6 导管内网纹宽度对压降和等效损失系数的影响

Tab.6 Effects of reticulated curl width on pressure drop and flow resistance coefficient

参数bv/μmΔp/PaQa/(10-13m3·s-1)ξ2.310.568.3010 955 数值3.010.678.2811 1684.011.118.2511 8955.011.578.2312 631

由表 6 可知，随导管内网纹宽度增加，网纹导管内平均流量减小，总压降增大，等效损失系数也逐渐增大，当导管内网纹高度增加到5.0 μm时，压降增大约9.56%，等效损失系数增大约15.30%.这表明，随着导管网纹宽度增加，网纹导管中的阻力增大，总压降减少，且流体过流面积减少，平均流量减少，输送能力降低.但对比网纹高度，其对等效损失系数的影响较小.

综合上述5种情况分析结果可发现，网纹模型使用伯努利方程建模，结合CFD数值模拟，可将木质部导管内壁网纹增厚产生的阻力机制用等效水头损失系数模拟，得出网纹高度对输送效率的影响最大，螺旋线数量的影响次之，网纹宽度和网纹螺纹间距的影响最小.因网纹高度的增加会导致导管流动壁面凸部在径向方向增大，会使壁面的回旋流动区域变大，导致等效内径更小，输送效率影响最大，网纹增厚其他参数变化相对网纹高度只单纯在结构阻力方面对输水效率的影响，因此对于网纹导管增厚水分输运最主要影响因素是结构变化导致的回旋流动区域大小的变化，回旋流动区域越大，等效内径越小，输送能力越低，反之则越高.

3.2 网纹导管内部流动特性分析

选取网纹增厚导管进行流场分析.其中模型长度为300 μm，内径为30 μm，纹宽和纹高为4 μm，轴向纹间距为20 μm，螺旋线数量为8，图5为网纹增厚导管中流体整体压力分布云图，图6为网纹增厚导管中速度分布云图.从图5中可以看出导管整体压力变化,其入口壁面压强较大，随着流体流动，压强均匀减小，当在近壁面遇到网纹凸部时，因流动遇到阻力，使流动方向产生突变，局部能量损失增大，使凸部前后产生了较大压差.图6中流体沿导管壁面流动的整体流速很小，由于增厚网纹的存在，使凸部壁面流动产生了局部回旋流动，此时导管流体流动的等效内径小于实际导管内径，也解释了网纹增厚参数变化导致流量降低，压降增大的原因.

图5 网纹增厚导管中流体的压力分布云图

Fig.5 Pressure contours in reticulated thickening vessel

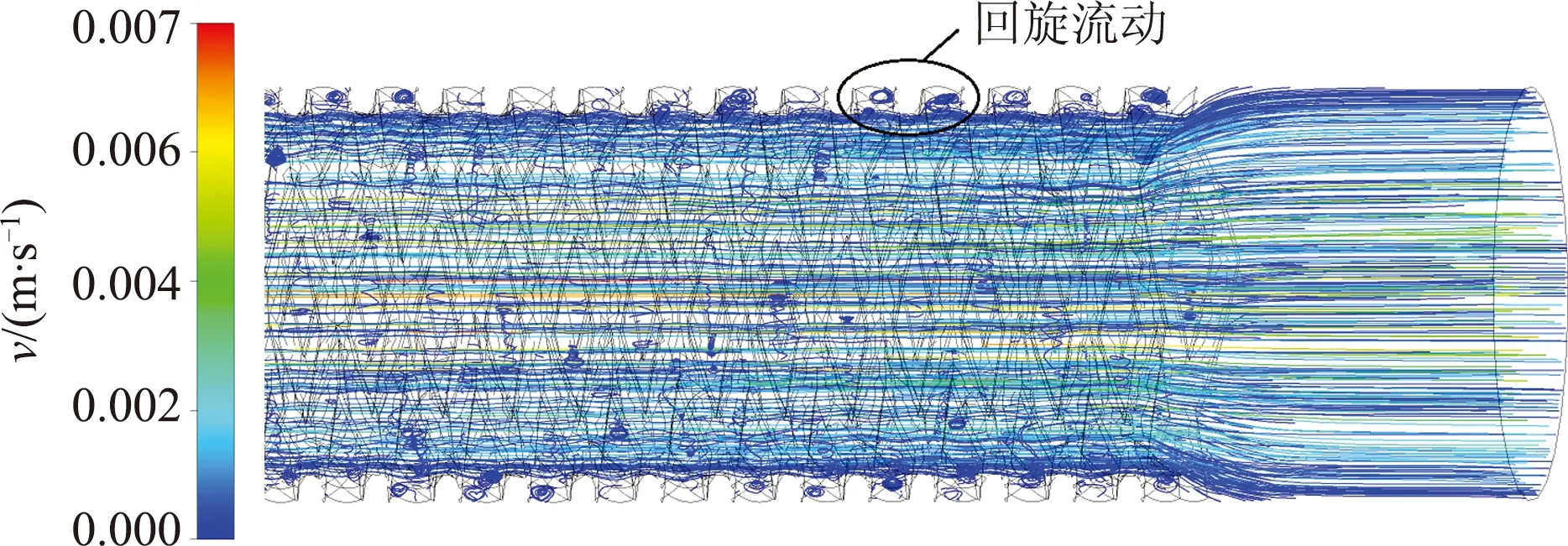
图6 流体沿导管壁面流动示意图

Fig.6 Fluid velocity contours and streamline in cross-sections in reticulated thickening vessel

3.3 不同类型增厚导管与光滑导管结构流阻分析

为了研究木质部导管的水分传输效率，对不同类型增厚导管和理想光滑导管进行比较分析(见表7)，计算导管由不同增厚结构引起的结构流阻，计算公式为

(9)

式中：F表示结构流阻；ξs为相同内径理想光滑管道的等效损失系数.显然，结构流阻越接近于1，导管的传输效率就越接近理想管道.

表7 不同增厚结构导管和光滑管等效损失系数计算值

Tab.7 Calculated flow resistance coefficients of different thickening vessels and smooth vessel

D/μmξ网纹管ξ螺纹管ξ环纹管ξ光滑管3011 89511 13211 4998 126404 3353 9344 1492 81950951895923426

选取网纹、螺纹、环纹3种不同类型增厚导管与光滑导管进行阻力分析，其中不同增厚导管的参数为长度为300 μm，纹宽和纹高为4 μm，轴向纹间距为20 μm，其中网纹导管的螺旋线数量为4；得到不同增厚导管等效损失系数见表6，D为导管内径，所示通过式(9)计算得出导管内径大小与导管的结构流阻之间的变化规律如图7所示.图中计算得出不同类型增厚导管的结构流阻θfr与导管内径大小成正比，增厚导管内径D越大，在其他设置条件一致的情况下，结构流阻越大.

图7 不同增厚导管的结构流阻与内径的关系

Fig.7 Relationship between flow resistance coefficientand inner diameter for different thickening vessels

3种导管增厚类型中网纹增厚导管整体结构流阻最大，环纹增厚导管次之，螺纹增厚导管最小.以导管网纹增厚为例，在导管内径D=30 μm 时，结构流阻的比值为31.67%;导管内径为D=50 μm 时，结构流阻的比值为55.21%，说明内径增加，导管增厚的结构引起的阻力所占比重越小，导管的流动特性越接近光滑管道.表7中，3种不同导管增厚结构，在导管内径较小时，导管等效损失系数大，说明内部结构特征影响水分传输效率大，因此作为3种增厚结构中最复杂的网纹结构其阻力最大，且网纹结构更容易使导管产生回旋流动区域，而环纹增厚比螺纹增厚阻力大的原因可能是螺纹与导管径向呈一定角度，对回旋流动区域产生一定扰动，使其回旋流动区域减小，阻力减小.在导管内径较大时，3种增厚结构对等效损失系数的影响基本一致，说明在导管尺寸较大时内部结构变化对流动阻力影响很小，这与文献[2，12]等研究结论相似.