轴流式水轮机顶盖强度及模态有限元分析

姚婷婷，郑源

(河海大学能源与电气学院，江苏 南京 210098)

在轴流式水轮发电机组中，顶盖是水轮机重要的支撑和过流部件，机组运行过程中所产生的轴向推力通过顶盖法兰向周围混凝土基础传递，顶盖的过流面承受着水压力的作用.顶盖与座环和水流直接接触，若顶盖在水流、机械等激励作用下引起共振，将传递至整个机组，尤其是在顶盖受力不均匀的状态下，振动更为明显，从而会导致结构产生疲劳破坏.顶盖刚度直接影响水轮发电机组的振动以及主轴摆动，顶盖强度将决定顶盖是否发生损坏.因此，顶盖既要满足其水力性能的要求，还要具有良好的刚强度特性和动态特性，以保证机组的安全稳定运行.

近年来，在水轮机结构特性方面，国内外学者进行了大量研究：钟苏[1]从拓扑结构、几何形状、板厚尺寸3个方面系统地对影响混流式水轮机顶盖刚度的主要因素进行了分析，发现筋板厚度、外法兰结构形式对顶盖轴向刚度影响较大；庞立军等[2]对带圆筒阀的水轮机顶盖轴向刚度的影响因素进行了分析；贾伟等[3]从顶盖刚度、强度等方面对国内某水电站轴流式水轮机顶盖进行了有限元分析，并对顶盖结构提出优化方案；岳志伟等[4]为了防止水轮机转轮引起的共振，结合流固耦合的办法，对其进行了模态分析；龙慧等[5]利用ANSYS Workbench软件对灯泡贯流式水轮机的座环进行了静力学分析和模态分析，为水轮机的座环以及整机的优化设计提供了一定的依据；梁权伟等[6]发现水轮机转轮在水中的一阶固有频率与转频类似，而且实际裂纹位置与水轮机应力集中部位一致，因此，可通过模态分析对电站产生振动的原因进行分析.

随着流固耦合技术的发展，许多学者对水力机械进行了基于流固耦合的应力特性和变形以及振动特性的研究，其准确度和有效性已获得了广泛的认可[7-8].然而，目前对轴流式水轮机组顶盖强度分析时，水压力载荷施加均采用恒定水压力，没有考虑到水压力的分布对应力特性及变形的影响.此外，目前关于轴流式水轮机动态特性的研究，主要是围绕转轮引起的共振、主轴、支撑系统、厂房等结构振动特性展开，关于轴流式水轮机顶盖振动特性的文献鲜见报道.

文中运用ANSYS Workbench平台对某轴流式水轮机在不同工况下进行全流道数值计算，得到顶盖过流面准确的水压力分布，利用单向流固耦合的方法将水压力载荷精确加载到顶盖表面，得到不同工况下顶盖的静应力分布、变形量和模态特性，从而实现对顶盖强度的校核与预测及动态性能分析，并对顶盖结构优化设计提供一定参考.

1 轴流式水轮机流场数值模拟

1.1 计算模型

以某电站轴流式水轮机为研究对象，对水轮机在不同工况下的流场进行数值模拟.在三维建模过程中，将整个水轮机组划分5个部分，分别为蜗壳、固定导叶、活动导叶、转轮、尾水管.轴流式水轮机的三维实体模型如图1所示.

图1 轴流式水轮机全流道模型

Fig.1 Complete flow passage model of axial-flow hydro-turbine

水轮机的基本参数分别为转轮型号ZZD32B-LJ-330，转轮直径3.3 m，设计水头Hd=33 m，设计流量Qd=69.5 m3/s，设计转速nd=214.3 r/min，转轮叶片数Z=6，固定导叶数Z0=12，活动导叶数Z1=24.选取设计水头(工况Ⅰ)、最小水头(工况Ⅱ)、最大水头(工况Ⅲ)、设计水头下甩负荷(工况Ⅳ)和最大水头下甩负荷(工况Ⅴ)5种工况进行计算，各工况基本参数见表1，表中H为水头，n为转速，Ψ为活动导叶转角，Ω为桨叶转角，P为水轮机出力功率.

表1 各工况基本参数

Tab.1 Operating parameters of five working conditions

工况 H/mn/(r·min-1)Ψ/(°)Ω/(°)P/kWⅠ最小水头31.00214.324511 438.6Ⅱ设计水头33.00214.324512 483.0Ⅲ最大水头39.01214.324515 695.3Ⅳ设计水头甩负荷52.24283.124525 993.2Ⅴ最大水头甩负荷61.39295.924529 934.6

1.2 计算方法

内部流场流动用连续性方程和Navier-Stokes方程联立求解描述，采用标准k-ε湍流模型来封闭方程组.采用有限体积法对控制方程组进行离散，扩散项和压力梯度采用有限元函数表示，对流项采用高阶求解格式.采用全隐式多重网格耦合方法对流场进行求解，将动量方程和连续性方程耦合求解.

1.3 网格划分

对流体区域进行网格划分.由于轴流式水轮机全流道过流部件多，几何形状较复杂，所以采用适应性较强的四面体网格划分，对转轮和导叶部分进行局部网格加密.对水轮机组网格划分进行无关性验证，以效率的相对差值为指标，设置收敛精度为10-5，当网格数大于378.00万时，效率的相对差值在0.1%以内.综合考虑计算精度与节省计算资源，最终确定网格总数为378.10万，蜗壳、固定导叶、活动导叶、转轮、尾水管网格单元数分别为38.33万，67.71万，68.23万，168.94万，34.93万.

1.4 边界条件

在ANSYS CFX上进行数值模拟计算，进出口边界条件设置为压力进口(total pressure)、自由出流出口(opening)，固壁面采用绝热无滑移边界条件(no slip)，转轮流体域与顶盖相接部分定义为流固耦合边界.采用近壁函数法对湍流流动的近壁进行处理，同时采用冻结转子法(Frozen rotor)设置座环与转轮和转轮与尾水管的交界面，处理旋转坐标系与静止坐标系流动参数的转换.

1.5 计算结果

计算得到5种工况下座环与顶盖交界面水压力的分布作为顶盖强度有限元计算的流固耦合表面荷载边界条件.由于各个计算工况的压力分布规律基本相同，只是数值不同，所以只给出设计水头工况下的压力云图，如图2所示.根据对5种工况下轴流式水轮机内流场分析表明，座环与顶盖交界面上导叶的进口处压力大，由外而内逐渐减小，具有明显的压力梯度.

图2 顶盖过流面压力云图

2 顶盖强度和模态分析

2.1 计算模型与边界条件

采用UG软件对研究对象进行三维实体建模，水轮机顶盖为钢板组焊件，分半把合，主要由大小法兰、内外环板、筋板等部分组成，其中顶盖的大法兰通过螺柱与水轮机座环相连接.顶盖过流面导叶活动部位设置不锈钢拉磨板，导叶全关位置处设鸽尾槽.顶盖内圆最小处直径为Φ3 310 mm.顶盖的材料为Q235-A，其性能参数分别为密度7 850 kg/m3，弹性模量2.06×1011Pa，泊松比0.28，屈服强度235 MPa.

由于顶盖结构复杂，故采用自由网格划分方式，设定单元大小为40 mm，并对导叶孔、台阶、筋板等部件进行加密，共生成23.90万个单元、43.70万个节点，顶盖网格如图3所示.

图3 顶盖网格划分

模型边界条件包括结构载荷和约束.2种结构载荷分别为惯性载荷和表面载荷.为了防止产生刚体位移，顶盖约束条件设置在顶盖与座环连接螺栓处，约束相应节点的自由度.顶盖约束与载荷的设置如图4所示.

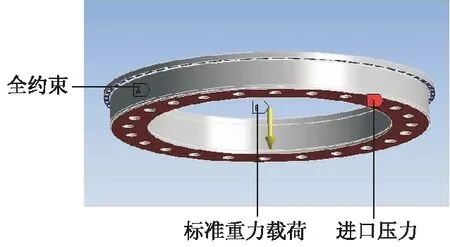
图4 顶盖载荷与约束

2.2 流固耦合计算结果

2.2.1 顶盖强度分析

通过ANSYS软件对顶盖在5种工况下进行有限元求解计算，得到顶盖的静应力分布及总变形，如表2所示.

表2 顶盖的最大静应力与最大位移

Tab.2 Maximum static stress and displacement in head cover

工况H/mσmax/MPaδmax/mmⅠ31.0042.8230.076 4Ⅱ33.0049.2210.087 9Ⅲ39.0157.7900.103 2Ⅳ52.2479.0430.141 1Ⅴ61.3991.3880.163 1

由表2可以看出，5种工况下计算最大静应力和最大位移均随着水头的升高而增大，这是因为加载在流固耦合面上的压力载荷随着水头的升高而增大.对顶盖进行强度校核时，取Q235-A的安全系数nb=3，材料的屈服强度为σs=235 MPa，许用应力[σ]=σs/nb=78.33 MPa.由此可见，顶盖在各工况下的最大静应力远小于屈服强度，所以顶盖在大部分工况下均能满足强度要求，顶盖的可靠性较高.在甩负荷工况下，顶盖最大静应力大于许用应力，在静应力、残余应力及动应力联合作用下，机组长期运行及多次甩负荷工况下会对顶盖产生裂纹破坏，故应尽可能避免在甩负荷工况下运行.

图5，6分别为5种工况下顶盖的总变形及静应力分布.由图5可以看出，不同计算工况下顶盖的变形趋势是相同的，最大变形发生在下面板圆孔间、辐向筋板圆孔处、内外圆环无辐向筋板支撑处.这是由于下面板直接承受水压力，下面板及内外圆环无筋板支撑，故变形较大.靠近顶盖与座环把合螺栓处有固定约束，故位移为0.

图5 不同工况下顶盖变形

图6 不同工况顶盖静应力分布

由图6可以看出，不同工况下顶盖的静应力变化趋势相同，顶盖的最大静应力分布在辐向筋板的圆孔处、下面板的圆孔之间、内外圆环与上下面板交接处.这是由于下面板直接承受水压力，下面板的圆孔之间无辐向筋板的支撑.在加载了流固耦合面的载荷之后，下面板厚度较薄，刚度和强度不足，所以造成了此处的应力集中和应力最大值，应力集中若周期循环将对顶盖结构产生疲劳破坏.为了防止疲劳破坏，应该尽可能的减弱应力集中，在不增加顶盖重量和工艺制造难度的情况下，适当地加大辐向筋板的厚度，以提高刚度；焊接部分应光滑过渡，避免产生尖角.

2.2.2 顶盖模态分析

分别对顶盖在无预应力和有预应力情况下进行模态分析，得到顶盖在空气中有、无预应力下的前6阶固有频率，如表3所示.

由表3可知，在有预应力的情况下顶盖的固有频率比无预应力情况下的稍有增大，这是因为在流固耦合作用下使顶盖产生了应力刚化现象，导致顶盖的固有频率有所提高.总体上，各阶频率增大均不高于0.5%，因此预应力对顶盖的模态分析的影响很小，在顶盖的模态分析中可以忽略.

表3 顶盖有、无预应力下前6阶固有频率

Tab.3 1stto 6thorder natural frequencies of head cover with and without prestress

阶次f/Hz无预应力有预应力ε/%1139.13139.620.3522139.22139.650.3093149.43149.980.3684149.45150.040.3955163.35163.950.3676169.95170.630.400

设计水头工况下(工况Ⅱ)有、无预应力的顶盖前6阶振型如图7，8所示，可以看出：在有预应力、无预应力2种情况下，顶盖的各阶振型基本相同；顶盖的第1，2阶振型相似，第3，4阶振型相似，仅存在着90°夹角的差别；第1，2阶模态为弯曲振型，第3，4阶模态为摆动振型，第5阶为顶盖下面板扭转振型，第6阶为顶盖的三瓣振动.由此可见，在低阶模态下，振动区域主要位于顶盖下面板处.

图7 无预应力下顶盖前6阶振型

图8 有预应力下顶盖前6阶振型

为了判断水轮机组在运行过程中是否发生共振的情况，将顶盖的模态频率与各种水力激振频率以及倍频进行比较.

1) 机组转频与机组转速相关,其计算公式为

(1)

式中：n为机组转速；k为阶次，k=1，2，3，….

2) 由导叶出口产生的不均匀流动引起的脉动频率，其计算公式为

(2)

式中：Z1为轴流式水轮机活动导叶数，Z1=24.

3) 水流从叶片进口到出口随着叶片的转动，所受作用力以一定的频率(即叶片的旋转频率)变化.叶片的旋转频率计算公式为

(3)

式中：Z为轴流式水轮机转轮叶片数，Z=6.

另外，由于其他因素所引起的振动频率难以用公式计算，需要实测得到.根据对上述计算结果比较可发现：顶盖流固耦合振动第1阶固有频率为139.62 Hz，而机组旋转造成的水动力不平衡低阶频率f1、导叶出口脱流引起的脉动频率f2以及叶片的旋转频率f3与之相差较大，因此发生共振的可能性较小.

3 结 论

1) 相对于以往只考虑顶盖的单一载荷研究，提出了一种基于单向流固耦合的方法对顶盖强度和模态进行分析.在甩负荷工况下，顶盖的最大静应力接近材料的许用应力.如果长期在甩负荷工况下运行，容易产生裂纹破坏.

2) 不同工况下，最大位移均发生在下面板无筋板支撑处、筋板圆孔处及内外圆环处.在下面板无筋板支撑处及内外圆环与上下面板交接处均发生应力集中，容易产生疲劳破坏.在不增加顶盖重量和工艺制造难度的情况下，适当加大辐向筋板的厚度，以提高刚度.焊接部分应光滑过渡，避免产生尖角.

3) 应用流固耦合技术，对顶盖在重力和水压力情况下产生的预应力模态进行分析，并与无预应力时的顶盖模态进行比较，结果表明，预应力对顶盖应力刚化现象不明显，因此在顶盖的模态分析中可以忽略其影响.此外，对顶盖固有频率进行了分析，并与机组旋转造成的水动力不平衡低阶频率、导叶出口脱流引起的脉动频率以及叶片的旋转频率进行比较，频率值相差较大，发生共振的可能性较小.