基于泛克里金插值的WSN位置指纹预处理*
2020-01-02乐燕芬张贺娜施伟斌
乐燕芬,张贺娜,施伟斌
(上海理工大学光电信息与计算机工程学院,上海 200093)
随着物联网、移动智能终端的快速发展,近年来位置相关的服务和应用,如展览馆、商场、仓库、机场等楼宇环境内基于位置的用户信息的传递导航等受到了广泛的关注。而无线传感器技术(WSN,Wireless Sensor Networks)由于其安装方便、即插即用、低功耗等特点广泛应用于智能楼宇中,使得基于WSN的室内定位的实用性和必要性日趋显著[1]。其中基于接收信号强度(RSS,Received Signal Strength)的方法由于不需要额外的硬件设备且具有非视距传输的特点而成为室内定位技术的重要实现手段。
基于测距RSS的定位技术要求基于信号传播特征建立无线信道模型再匹配测量数据完成定位[2]。这就要求模型能精确反映空间的信号传播特性。而室内环境有墙体等障碍物存在并有较频繁人员活动,使得无线信号因多径效应、斑块效应等出现扰动,表现出复杂、时变的传播特性,使得由信号强度估算传播距离有较大的误差,因此也有文献采用多维标度法,直接利用无线信号强度进行定位以期克服扰动对定位的影响[3]。
RSS定位算法的另一类是位置指纹识别法。该方法通过离线阶段采集的监测区域内的采样点RSS获得该区域信号分布的指纹描述。在线阶段通过测量信号与指纹的匹配来估计目标位置。这种方法不需要预设信号的传播衰减模型,更关注离线与在线阶段的RSS信号是否具有一致的分布模式。对于RSS指纹定位技术目前的工作集中在2个方面,一个是定位匹配算法的研究,包括基于机器学习的建模[4]、特征提取[5]等寻求RSS信号与位置的非线性关系;另一个研究重点在于位置指纹库的构建。后者主要的研究目的就是在保持甚至提高定位精度的前提下尽可能降低离线阶段建立位置指纹库所需的人力、时间成本。在此研究方向目前也已有不少的研究成果。如文献6采用德洛内三角剖分(Denaunay Triangulation)算法,把所有采样点进行三角形网格划分,以采样点为顶点构成的三角区域内的插值则通过该3个采样点线性生成[6]。文中的实验表明该算法与反距离加权插值(IDW,INVERSE DISTANCE WEIght)有相当的插值精度。由于RSS信号衰减与传播距离总体上并不满足线性关系,为了克服此线性插值的不足,文献7提出了三次三角插值。该方法用二元三次多项式描述三角区域内RSS信号强度与三角形顶点的距离关系,从而确定插值点的RSS值[7]。这在一定程度上解决了线性插值的局限性。但德洛内三角剖分纯粹从离散几何角度出发,按采样点的绝对物理位置坐标进行划分,并不考虑室内具体环境的布置和构造对RSS信号的影响。近年来,克里金方法(Kriging)也逐渐被应用到室内定位的RSS插值中,并针对室内RSS信号的分布特点,进行了各种方式的探索和改进。如文献8在用普通克里金(OK,Ordinary Kriging)插值时用模拟退火算法改进了理论变异函数的拟合精度[8];文献9则采用RSS信号与链路通讯质量LQI作为主辅变量,利用协同克里金法完成空间插值[9];而文献10针对不同时间段内室内人员活动度不同,采用普通克里金插值法构建相应时段的位置指纹库[10]。上述方法都利用了RSS信号的空间相关性,用克里金方法挖掘RSS信号在空间的分布特性,但应用这两类克里金方法的前提是,空间变量也即RSS信号在监测区域内具有一致的变异性,也即样本数据具有同样的期望和方差。而对于RSS信号,在整个监测区域内测量值不可能为常数。不仅是因为复杂的室内环境,同时也因为无线信号总体上随传播距离的增加而衰减。这使得这两类克里金插值算法在生成RSS指纹库时有其局限性。
针对此问题,本文提出了一种基于泛克里金(UK,Universal Kriging)插值的指纹预处理方式,通过漂移函数的加入解决传播距离引起的RSS信号衰减,用变异函数描述室内环境下RSS信号的空间变化,并以一个典型办公区域为例,通过环境分析结合RSS值的分布确定变异函数的形式,对真实RSS指纹进行插值构建位置指纹库。通过在线阶段加权K近邻算法验证了所构建指纹库对降低离线人力时间成本及提高在线定位精度的有效性。
1 泛克里金插值算法原理
克里金插值法又称空间局部插值法。该方法考察空间属性在空间位置上的相关性与变异分布,由待插值点影响距离范围内的采样点来估计待插点的属性值,是有限区域内对区域变量的一种无偏最优估计。普通克里金插值法计算公式为:
(1)
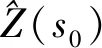
变异函数γ也称为半方差函数,定义为:
(2)
该函数只与采样点间的分离距离h有关,而与位置s和s+h无关,反映信号的空间结构性和随机性变化。实际应用时,常用样本变异函数拟合获得理论变异函数。样本变异函数的计算采用下式:
(3)
式中:Nh是分离间距为h的采样点对个数,是随h变化的量。样本变异函数给出了当前采样空间内信号的离散变异结构,通过拟合的方式获得理论变异函数来表征采样空间内任意距离下的信号变异特性。球状模型、指数模型、高斯模型等都是常用的拟合函数模型。
普通克里金法要求信号满足二阶平稳假设,即E[Z(s)]=m,m在空间上是常量。而实际应用中空间信号很难满足此假设,也即E[Z(s)]=m(s),是空间位置s的非平稳函数。针对这种情况,泛克里金插值通过增加一个确定性漂移,把在位置s上的信号表示为:
Z(s)=m(s)+r(s)
(4)
式中:m(s)为采样信号的确定性漂移函数,也称趋势;r(s)是期望为0的残差量,满足二阶平稳条件。漂移形式需依据背景资料分析、样本变异函数的图形观察来确定[11],如文献12中f(s)采用路径结合墙壁的信号衰减模型[12],更常用的是采用位置s相关的多项式来表达[11,13-14],此时m(s)用P个坐标相关函数fp(s)的线性组合来表示:
(5)
这样,泛克里金插值公式可表示为:
(6)
式中:
(7)
按照无偏估计的原则,要求下式成立:
(8)
即要满足:
FTW=F0
(9)
式中
F0=[1,f1(s0),…,fP(s0)]T
(10)
此时估计方差可表示为:

(11)
式中:
(12)
γ=[γ(s0-s1)…γ(s0-sN)]T
(13)
这样问题就转化为:
(14)
采用Lagrange乘数法解决此问题,可以得到一个线性方程[15]:
(15)
式中:λ是引入的Lagrange算子。解此方程可得权重系数wn。
实际应用时,根据式(3)获得样本函数,拟合后获得理论变异函数γ,而本文的漂移函数采用二元二次多项式,表示为:
(16)
式中:(x,y)是位置点s的坐标,系数β=[β0,β1,…,β5]T是待定的回归参数,Fs=[1,x,y,x2,xy,y2]T。
图1给出了基于泛克里金插值的指纹预处理过程。通过对离线采集的RSS信号预处理,分析信号的空间分布趋势,对监测区域进行划分。对每个区域通过变异函数和漂移函数的拟合,按照无偏和最小方差的准则,利用Lagrange乘数法求解获得插值权重。确定区域的插值密度,对离线指纹库插值后构建预处理后的位置指纹库。利用该指纹库可完成在线阶段的位置估计。

图1 基于泛克里金插值的指纹库预处理过程
2 基于泛克里金的RSS插值
2.1 数据预处理
在WSN室内定位中,采集的样本数据是每个参考点接收的来自各个锚节点的RSS信号。首先需要分析数据的空间分布趋势。实验监测区域为40 m×15 m的办公楼面,包括两侧走廊和中央大厅。在两侧走廊天花板上间距4.2 m共布置了18个锚节点,分别标记为#1~#18。整个监测区域内间隔1.8 m设置参考采样点,共90个。
图2给出了位于(33.8,14.4)坐标的#18锚节点在每个采样点的RSS测量值。由于信号的RSS值在负几十dBm范围,为了直观显示信号强度,显示的时候每个RSS测量值加了100。从图中可看出,不同采样点采集的RSS信号强度变化较大,甚至在某些采样点无法采集到有效的RSS信号。针对实际物理环境中RSS的分布,引入漂移函数来描述区域内RSS信号的非平稳或区域异常变化;其次针对具体的监测观察区域,可根据物理布局划分多个子块进行变异函数的拟合,避免出现在全局范围进行变异函数拟合时过于复杂、难以拟合的情况。

图2 RSS信号在各采样点的强度分布
2.2 拟合的变异函数和漂移函数
变异函数主要描述空间不同采样距离与信号之间的关系;而这个关系在复杂室内环境下具有很强的局部性,随空间布局而变化。图3虚点线给出了4个锚节点在中央大厅区域采样点的样本变异函数。横坐标是归一化的分离距离。从图3中可看出,处于空间不同位置的每个锚节点有自己独特的变异函数。针对此实验现象,为更准确描述信号的空间分布特性,对每个锚节点分别进行变异函数拟合。

图3 样本变异函数及拟合的理论变异函数
变异函数模型目前常用的有球状模型[8,15]、高斯模型和指数模型,也有文献采用高次多项式进行拟合[13-14]。具体采用何种理论模式可根据插值区域样本变异函数的趋势进行选择,使拟合结果较优。本文采用交叉验证法进行检验,保证插值的剩余误差平均值和方差最小[13]。图3中实点线是其中#1、#6锚节点基于模型获得的理论变异函数。这两个锚节点分别采用指数模型和高斯模型确定理论变异函数。从图中可看出不同锚节点拟合后的变异函数存在较大的差异,说明分布于走廊末端的1号锚节点与分布在中央大厅边侧的6号锚节点具有不同的信号传播衰减特性,同时也表明在室内环境下,锚节点的分布会影响信号的变异模型。
通过实验中采集的样本数据,采用最小二乘法确定了漂移函数的系数β。表1给出了其中几个锚节点的漂移函数系数。

表1 各锚节点漂移系数
2.3 插值结果与分析
图4分别给出了#1与#12锚节点基于中央区域64个采样点,插值形成484个位置指纹的RSS分布图。每个锚节点插值时采用相应的变异函数参数和漂移系数。从图4可看出锚节点有各自的RSS分布特性,插值形成的RSS与实测值基本吻合。

图4 插值后的RSS分布
为了进一步分析拟合模型的有效性和准确性,采用了交叉证实法,从中央区域的64个采样点,选取1个测量值,并从采样值序列中暂时去除该值,利用余下的63个采样点确定变异函数参数和漂移系数。再利用泛克里金预测该采样点的估计值,并与实际测量值进行比较。图5逐点给出了采样区域内3个锚节点各自的拟合残差,平均拟合残差分别为4.3 dBm、3.5 dBm及9.1 dBm。从图中可看出,某些位置的拟合残差较大,甚至达到了20 dBm。分析采样数据可发现,这些采样点由于某些原因均未收到相应的锚节点信号,在指纹库中记录为-100 dBm,与其周围采样点的信号值有较大异常,很难用模型精确描述,插值结果也相对误差较高。

图5 拟合精度比较
3 定位精度分析
为了评估所提泛克里金插值方法构建指纹库的性能,在监测区域内随机挑选了26个位置点在线采集RSS信号,基于不同的位置指纹库,利用WKNN(WeightedK-nearest Neighbor)[16-17]算法进行定位。该算法比较在线采集的RSS信号与指纹库内各指纹的欧氏距离,选取距离最小的K个指纹,并取欧氏距离的倒数作为权重,利用这K个指纹位置的加权平均作为估计位置来完成定位。本实验中K取4。表2给出了相应的平均定位误差。其中OK或UK分别指普通克里金插值和所提的泛克里金插值,其后的数字表示插值后形成的指纹库的指纹数量,比如UK_484表示采用泛克里金插值形成484个指纹。IDW插值时采用了2种方法:IDW_484表示利用全部采样点估计形成484个指纹,而IDW6_484则表示利用距离最近的6个采样点插值估计形成484个指纹,其中距离指数都取2。

表2 基于不同指纹库时的定位精度比较
由表2首先可知,不管采样密度大小,基于UK_484指纹库的定位精度均高于OK_484、IDW_484、IDW6_484及原指纹库;当间隔1.8 m进行采样,利用UK算法插值形成484个参考指纹后,定位精度甚至达到0.86 m,相比较基于原指纹库的定位误差1.56 m,定位误差降低约45%;其次随着插值点数量的减小,相应的定位精度也有所降低,但UK_225仍具有与OK_484相近的定位精度。
同时也可观察到,随着采样点的稀疏,并不是插值密度越大,构建的指纹库越能反映RSS分布特点。比如采样点数量为16个时,UK_225的定位精度相对最高,而几种不同方法生成的484插值点构成的指纹库定位精度反而降低。这说明插值要根据采样点的间隔选择合理的插值密度。结合表中64个采样点时基于UK_484的定位精度最高,而32个和16个采样点时,分别是基于UK_225和UK_100指纹库的定位精度相对高,说明6倍~8倍的插值密度较合适。另外从表中也观察到,利用32个采样点插值形成的UK_225与包含64个采样点的原指纹库的定位精度相当,说明适当降低离线阶段的采样数量,插值构建指纹库后依旧可以得到相当的定位精度。
本实验中走廊两侧共布置了18个锚节点,本文也分析研究了插值精度与锚节点数量的关系。表3给出了基于不用数量锚节点,利用UK插值构建指纹库的定位误差。

表3 锚节点数量对指纹库构建精度的影响
从表3可看出,在本文实验区域内,包含12个锚节点构建的指纹库定位精度最高,而锚节点数量的减少对指纹库精度影响不大,如在5个锚节点的情况下,UK_484的平均定位精度仍然达到了将近1 m;而过多的锚节点反而会引起定位精度下降。这也说明多个锚节点的RSS信号存在冗余,并且这种冗余反而使RSS的特征模糊,不利于定位匹配。在实际应用中,锚节点的数量也需要与监测区域面积相匹配,布置过多的锚节点可能使RSS信号特征模糊,并不一定有利于定位精度的提高。
4 结束语
本文针对基于RSS信号的指纹定位技术,提出一种基于泛克里金插值的指纹预处理方式。根据每个锚节点RSS信号空间分布特点,构建相匹配的变异函数和漂移函数找到位置与RSS信号的关系,通过插值形成分布密度高的位置指纹从而降低离线阶段的人力、时间成本或提高在线定位精度。实验结果表明,①基于此方法构建的离线指纹库在采用同样的在线定位算法时有更高的定位精度,在本实验中原始1.8 m的参考点密度经插值后定位精度可达约0.9 m;②为使构建的位置指纹库能有效体现RSS信号的空间特性,插值点数量与采样点的数量宜在6倍~8倍;③需根据监测定位区域选择合适数量的锚节点以构建最能反映空间信号特征的位置指纹库;④基于泛克里金插值的指纹预处理方式能有效降低离线阶段的人力和时间成本。
