雷电快电场测量仪幅频特性的时域标定方法研究*
2020-01-02石立华周颖慧
贾 晟,石立华*,邱 实,孙 征,李 云,周颖慧
(陆军工程大学电磁环境效应与光电工程国家重点实验室,南京 210007)
自上世纪70年代以来快电场测量仪开始被应用于自然闪电和人工引雷情况下地面垂直电场的测量[1-3]。快电场测量仪可以捕捉雷电过程中的瞬态变化,记录电场波形变化细节[4],使得其在闪电起始过程定位[5]、通道特性研究[6]等方面发挥重要作用,成为雷电观测的基本手段之一。
IEEE标准指出,校准电磁脉冲传感器时域参数时,应该考虑其频域的特性。标准中给出了两种校准方法,标准天线法和标准场法[7]。其中,标准场法的校准原理是:为待校准的传感器提供可准确计算的参考电场,将传感器置于电场环境中校准测量。该标准中指出产生标准电场的设备包括TEM室、GTEM室、波导等设备。TEM室(Transverse Electromagnetic cell)结构简单,检测方法简便,可以产生均匀性良好的电场,作为标准电场[8-9]。其内部电场幅值可通过输入电压与结构尺寸参数计算出,其金属外壳可以屏蔽外界电磁环境干扰和避免内部电场对外界辐射,提高了实验结果的可靠性[10]。
幅频特性曲线常用的标定方法为频域标定法,原理是将连续正弦波作为激励馈入到TEM小室,测量每个频点处传感器的响应与馈入的连续波幅值,绘制传感器的幅频特性曲线[11]。除此以外,还可以通过时域方法标定传感器的幅频特性曲线。由传感器输入、输出时域波形建立传感器的数学模型,描述系统的传递函数,最终得到该传感器的幅频特性曲线。这种时域标定方法属于系统辨识理论的范畴,当前一些学者运用该方法来研究传感器的特征参数。石立华等[12]人研究了脉冲磁场传感器的时域标定问题,基于系统辨识理论建立了传感器的时域模型和误差修正模型。孟萃等[13]人建立了时域动态模型来研究核电磁脉冲传感器的灵敏度系数一致性问题。谭坚文等[14]人采用时域方法针对脉冲电流探头的输出波形低频失真建模及校正。
快电场测量仪用于捕捉雷电过程中的细节事件。由于设计传感器时灵敏度与时间常数不能兼顾[4],因此传感器输出信号中存在低频失真的现象。若想通过传感器所记录的波形还原电场变化,那么补偿低频失真是关键内容。因此,使用前需要明确传感器的幅频特性[15-17],在波形失真的情况下根据时域波形对实测数据实现动态校正补偿,是传感器响应信号后处理的重要环节。
本文基于输入-输出误差模型理论,依据标准场法的校准原理,搭建了快电场测量仪幅频特性曲线标定系统,采用最终预报误差法辨识模型阶数,建立传感器系统的最优模型,对快电场测量仪(以下简称“快天线”)幅频特性展开时域标定,并与频域标定结果和时域FFT标定结果作对比。通过设计快天线的逆系统,对输出信号补偿低频失真,还原真实电场变化。实验结果表明,基于输入-输出误差模型的时域标定法能够准确标定快电场测量仪的幅频特性曲线,所设计的逆系统可以很好的还原电场信号。
1 传感器幅频特性标定方法
传感器幅频特性标定方法可分为时域和频域标定。频域标定是采用不同单频点的连续波来标定传感器的幅频特性特性曲线,而时域标定本质上是建立数学模型来求解传感器的传递函数。
1.1 幅频特性频域标定方法
将不同单频点连续正弦波馈入TEM小室,记TEM小室输出电压为V1,快天线响应电压为V2,记录实验中每次TEM小室输出电压V11、V12、V13、V14、V15……和对应的快天线响应电压V21、V22、V23、V24、V25……,则幅频响应H(f)可以表示为:
(1)
根据式即可绘制出传感器的幅频特性曲线。
1.2 幅频特性时域标定方法
1.2.1 输入-输出误差模型理论
系统辨识理论作为一种“黑箱”建模理论,在电磁脉冲传感器时域测量与波形校准等方面发挥了重要作用。
输入-输出误差模型是系统辨识理论中的一种线性时不变模型。它是采用数学的方法对系统的输入、输出数据提炼出数学模型,该模型以紧凑形式描述系统的传递函数,表达出系统的动态特性[18]。
快天线电场传感器可视为线性移不变(LSI)系统,设输入信号为u(k),输出信号为z(k),则有:
(2)
式中:B(z-1)=b0+b1z-1+b2z-2+b3z-3+…+bmz-m,A(z-1)=1+a1z-1+a2z-2+a3z-3+…+anz-n,ε(k)是误差项。因此对于传感器系统,其传递函数H(z)可用多项式B(z-1)和A(z-1)表示,
(3)
从z域变换到频域,根据z=ejω和ω=2πfi/fs,所以,
(4)
因此,可以通过数学模型的传递函数获得传感器系统的幅频响应等信息。
1.2.2 模型阶次辨识
为使所建立的数学模型与实际系统高度吻合,式中B和A的阶数nb和na是重要的影响因素。本文采用最终预报误差法FPE(Final Prediction Error)来辨识模型阶数nb和na,建立最优数学模型。最终预报误差法是选用预报误差项作为准则函数,当预报误差项最小时,其对应的阶数就最接近真实模型的阶数,此时的数学模型将与实际系统一致性很好。
考虑到实验系统本身存在的白噪声,将式改写成最小二乘格式,
z(k)=hT(k)θ+ε(k)
(5)
式中
(6)
因此,预报误差可表示为
(7)
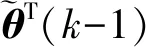
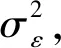
(8)
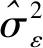
1.2.3 时域分步标定
方波具有丰富的频域分量,其上升沿含有高频分量,可以反映出传感器的高频响应特性,其“平顶”降落可以反映出传感器的低频响应特性。受普通示波器采样深度的限制,要想获得系统准确的高频和低频信息,需要采集不同时间尺度的输入和输出波形。因此,在时域标定过程中选择不同脉宽的方波作为输入波形,分步标定快天线的高频和低频响应。
1.3 幅频特性时域FFT标定方法
设传感器输入信号为x1,输出响应为y1,对传感器的输入与输出时域波形分别做傅里叶变换,对应的频域为|Fx|、|Fy|,则频域响应H(f)为
(9)
由式可得传感器的幅频特性曲线。
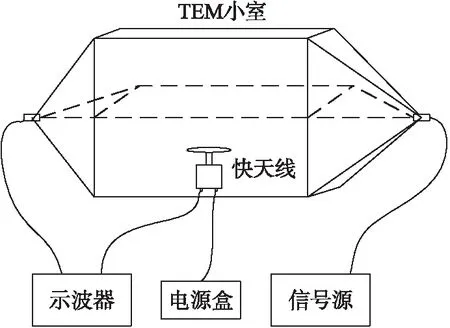
图1 实验设置图
2 幅频特性标定实验
2.1 实验系统设置
本文基于TEM小室搭建了标准场校准系统[19],实验设置如图1所示。实验中采用Rigol DG4162型函数/任意波形发生器(以下简称“信号发生器”)作为信号源,内阻为50 Ω,其特点是输出波形稳定,幅值准确,波形失真程度低,用于输出稳定连续的正弦波和方波。采用Tek 3024型示波器采集数据,该示波器带宽范围可达200 MHz,采样率为2.5 GHz,最小水平分辨率为2 ns/格,最大垂直分辨率为 10 mV/格,完全满足实验要求。实验时,设置示波器通道内阻均为50 Ω。
将快天线连接电源,置于TEM小室的下层空间中央位置,保持天线的圆形平板与TEM小室的中间隔层平行,避免由于人为因素引入实验误差。信号发生器输出端口通过同轴线向TEM小室馈入激励信号。TEM小室另外一端通过同轴线连接至示波器通道一,监测馈入TEM小室的波形;快天线的输出端口连接至示波器通道二,监测快天线响应。
2.2 频域标定
将不同频点的正弦波馈入TEM小室,在小室下层空间产生均匀电场作为传感器输入,快天线的响应幅值随频率变化而动态变化。实验时利用信号发生器产生幅值为20 V、不同频率的正弦波,注入TEM小室,按照每十倍频程记录一组TEM小室输出电压V1和快天线响应电压V2(根据具体情况可以适当增加频点数)。根据式,连续正弦波标定快天线幅频特性曲线的结果如图2所示。从图2中可以看出由于读数误差的存在,幅频曲线高频部分光滑程度较差,快天线-3 dB带宽范围约为200 Hz~6 MHz。
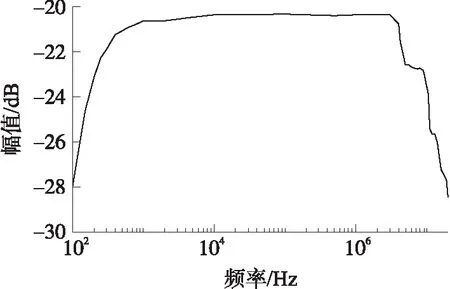
图2 连续波标定幅频曲线结果
2.3 基于输入-输出误差模型的时域标定
2.3.1 传感器高频响应标定
设置示波器采样率为2.5 GHz,采样长度为10k个点,示波器水平分辨率为40 ns/格。为了更好获取快天线高频响应,向TEM小室注入频率为1 MHz的方波,采集输入与输出波形,建立数学模型。选取目标数据段,即输入波形和输出波形的上升沿,如图3(a)所示。
根据FPE定阶法,选取最终预报误差最小情况下的模型阶数作为最优模型阶数。确定多项式B和A的阶数分别为6、6,传递函数H(z)为
H(z)=(5.358×10-4+0.003 8z-1-9.755×10-4z-2-
0.007 5z-3+2.696×10-4z-4+0.003 9z-5)×
(1-0.079z-1-2.851z-2+0.131 5z-3+2.73z-4-
0.056 7z-5-0.876z-6)-1
(10)
比较模型输出结果和传感器输出结果,波形吻合程度高达96%,如图3(b)。将H(z)由z域变换到频域,因此可求出快天线传感器高频部分幅频响应,如图3(e)。快天线高频的-3 dB带宽范围(即>-23 dB范围内)是<7 MHz。
2.3.2 传感器低频响应标定
设置示波器采样率为1 MHz,采样长度不变,水平分辨率为200 μs/格。向TEM小室注入方波信号,频率为400 Hz,获得快天线传感器的低频部分响应,如图3(c)。选取波形时确保“平顶”部分完整。根据FPE定阶法,分别确定多项式B和A的阶数为6和9,其传递函数H(z)为
H(z)=(0.0611+0.0993z-1+0.0226z-2-0.0569z-3-
0.0834z-4-0.0426z-5)(1+1.198z-1-0.358z-2-
1.1545z-3-0.926z-4+0.0088z-5+0.448z-6+
0.1537z-7-0.159z-8-0.2035z-9)-1
(11)
比较模型输出结果与传感器响应结果,模型辨识结果与传感器输出结果吻合程度为95.6%。根据系统传递函数求出快天线低频部分的幅频特性曲线,如图3(f),快天线低频的-3 dB带宽范围是>200 Hz。
基于输入-输出误差模型时域标定幅频曲线结果较为光滑,高频段和低频段连接部分幅值差小于0.2 dB,误差在可接受范围内。
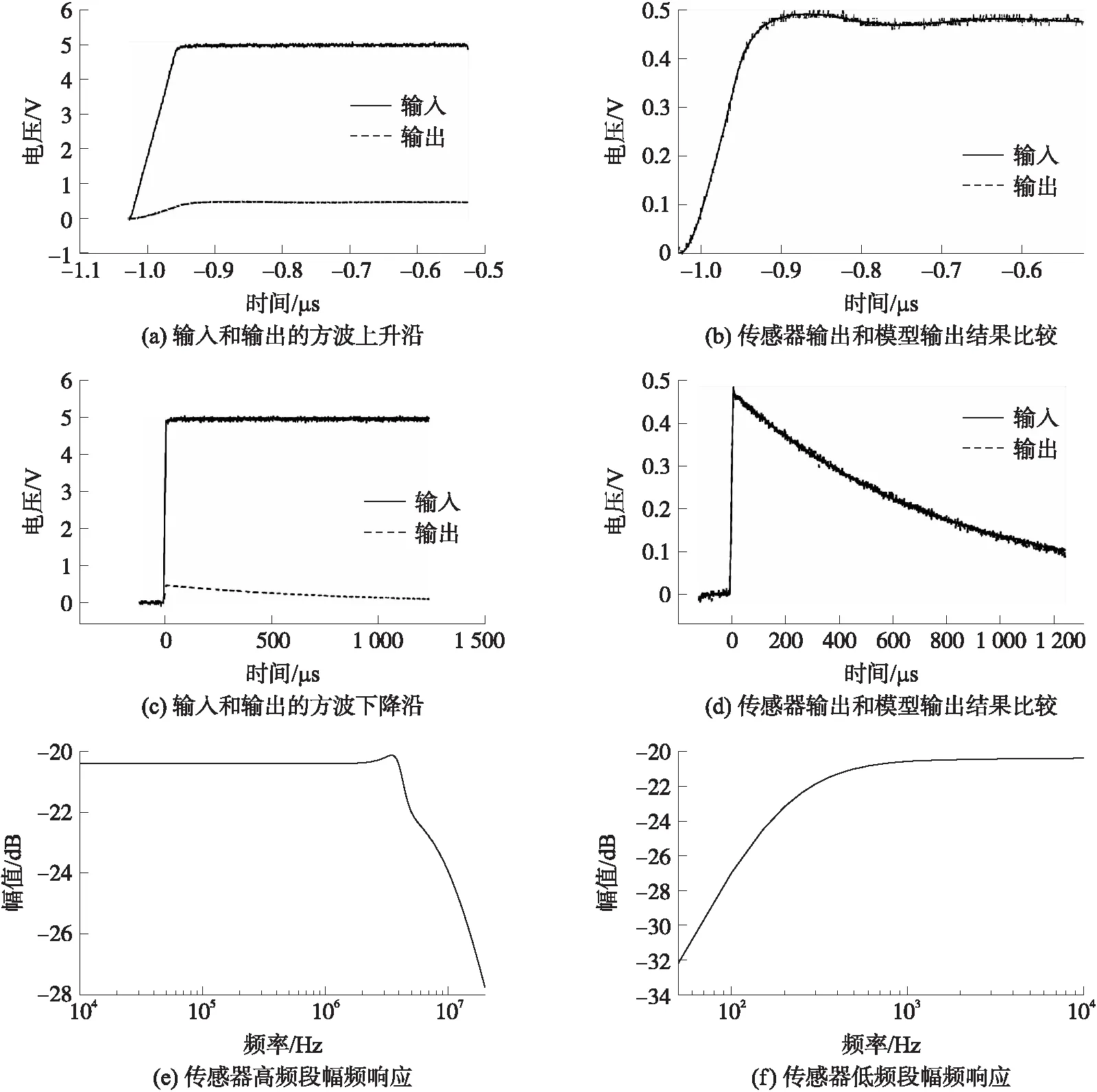
图3 基于输入-输出误差模型的幅频特性时域标定结果
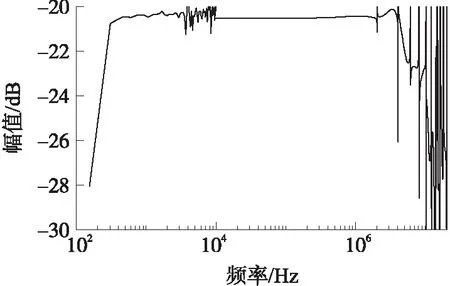
图4 时域FFT标定结果
2.4 时域FFT标定
仍选用基于输入-输出误差模型时域标定的数据计算传感器幅频特性曲线,结果如图4所示,通过比较可以看出傅里叶变换获得的曲线效果较差,由于高低频内噪声的存在,图4中曲线振荡严重,突出体现在3 MHz以上和3 kHz~10 kHz之间。采样长度不足的问题导致低频段的幅频曲线上点数较少,曲线光滑度较差。
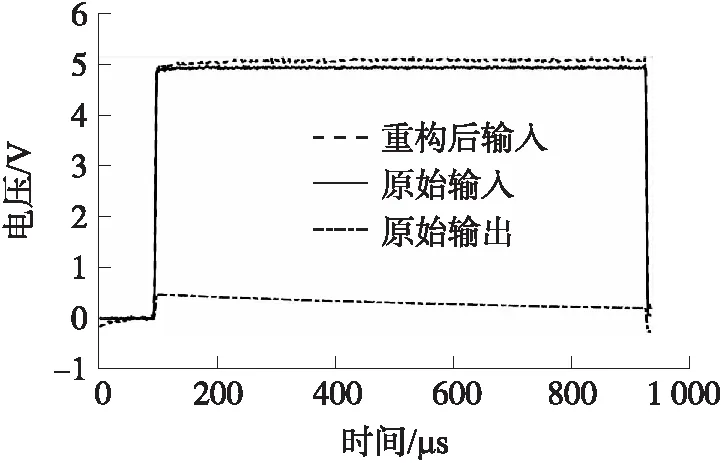
图5 模型重构结果与原始输入对比
3 波形失真补偿
对失真波形补偿,本质上是设计快天线的逆系统,对失真波形重构。建立快天线的逆系统模型,将快天线响应作为模型输入,模型的输出就是实际上快天线的输入。以图5中快天线输入和失真波形为例,通过重构逆系统、模型辨识,确定逆系统传递函数H(z)为
H(z)=(10.38-3.526z-1-4.17z-2+1.11z-3-5.52z-4-
8.71z-5+6.44z-6+1.91z-7-2.11z-8+4.19z-9)×
(1-0402z-1-0.354z-2+0.1996z-3-0.619z-4-
0.837z-5+0.661z-6+0.156z-7-0.272z-8+
0.5z-9-0.0325z-10)-1
(12)
根据逆系统传递函数得到重构后的波形如图5所示。对比模型输出和快天线输入,重构结果很好,波形趋势一致。
4 结果对比与分析
①图6(a)为频域标定结果和基于输入-输出误差模型时域标定结果的对比。对比幅频特性曲线频域标定结果和时域标定结果,可以看出,两种方法的结果的“平顶”部分吻合程度基本一致。在传感器系统响应-3 dB带宽范围内,时域标定结果与频域标定结果一致。在-3 dB带宽范围外,两种方法所得结果的吻合程度也比较高。图6(b)为时域FFT标定结果和基于输入-输出误差模型时域标定结果的对比,模型辨识方法的优越性非常明显。
②幅频曲线标定结果可以看出,在低频截止频率段与高频截止频率段,快天线灵敏度系数可看作频率f的函数,而在中频段,快天线响应幅值与输入信号频率大小无关,可看作一常数。因此在截止频段使用峰值标定传感器灵敏度是没有意义的,即在标定传感器灵敏度之前,应首先明确传感器的幅频特性。
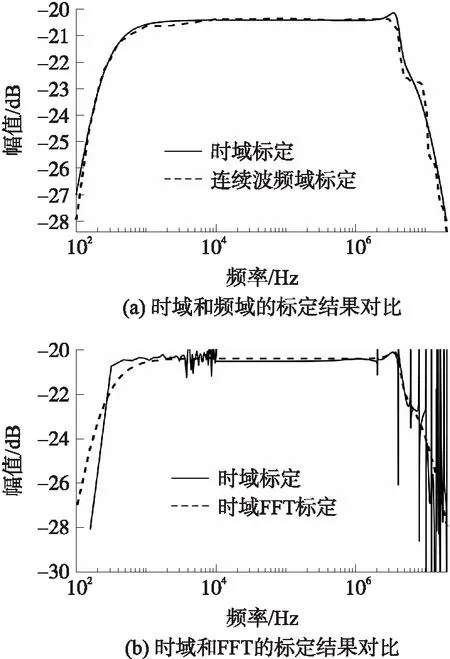
图6 连续波频域标定、时域标定和时域FFT标定结果对比
③频域标定法、基于输入-输出误差模型的时域标定法和时域FFT标定法比较:

基于频域测量的幅频曲线标定法基于时域测量的输入-输出误差模型标定法基于时域测量的FFT标定法实验设备连续波信号源加接收机,或网络分析仪脉冲信号源加示波器脉冲信号源加示波器特点小信号测量、非参数化的幅频曲线脉冲大信号测量、参数化模型脉冲大信号测量、非参数化模型应用获知频带特性,获得通频带内的幅度校准系数获知波形响应特征、频带特性,获得全波形的校准模型,可直接用于失真恢复获知波形响应特征、频带特性,FFT和逆FFT在高频段噪声影响严重
④幅频特性曲线标定过程中,确保实验步骤连续,一次性完成数据采集,以保证传感器和相关实验设备所处状态一致。
5 传感器标定结果的实际应用
本文方法获得的电场传感器标定结果不仅为确定传感器灵敏度系数和响应带宽提供了描述参数,同时也为校正传感器失真提供了有效方法,在雷电电磁场波形的准确测量中获得了应用。
图7为一次地闪回击过程的快慢天线测量结果及快电场传感器的校正结果。其中,慢天线通常用于测量雷电过程的电场慢变化,主要反映放电过程的电荷变化引起的电场抬升,这类天线具有较大的时间常数,低频特性良好;而快天线主要反映电场快速变化,低频响应不足,因此存在后沿保持能力不足,类似于图3(d)中的“平顶下降”现象。利用实验室阶跃波标定获得的结果,根据建立的快天线逆系统模型对实测快天线数据低频补偿,并将结果与慢天线数据对比。
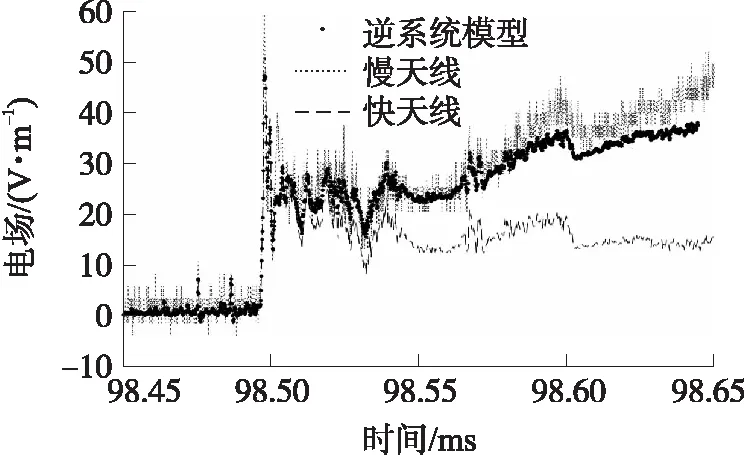
图7 模型补偿结果与实测结果比较
由图7可看出,对快天线数据做低频补偿后取得较好的效果,后沿得到有效校正,与慢天线反映的电场抬升趋势吻合一致。
6 总结
本文基于输入-输出误差模型理论对快电场测量仪建立数学模型,分步计算出快电场测量仪的幅频特性曲线,并与频域标定方法、时域FFT标定方法作比较。建模过程中采用最终预报误差法(FPE)确定传递函数的最优阶数,提高了模型吻合度。本文设计了快电场测量仪的逆系统模型对失真方波和实测雷电电场数据校正补偿,均取得了较好的结果。
