失配诱导光热敏感凝胶-橡胶双层梁弯曲行为分析

颜慧贤，董 则

（1.三明学院 机电工程学院，福建 三明 365004；2.三明学院 装备智能控制福建省高校重点实验室，福建 三明 365004）

刺激响应性水凝胶是近年来备受关注的新型智能材料[1-3]。 这类材料可以对温度、pH、湿度等因素的变化作出积极响应而发生体积、形状的变化，在人造肌肉、软机器、机械手和爬行器等领域具有广泛应用前景[4-6]。 凝胶应用于这些领域时，常需要粘附于基底，利用凝胶与基底溶胀系数的失配使复合结构发生弯曲，从而实现致动效应[7]。 对于层状凝胶复合结构的弯曲行为，国内外学者展开了相关研究并取得了一定的成果。 Cai 等利用梁理论对粘附于不可压弹性基底的中性凝胶双层复合结构的弯曲行为进行研究，并比较了采用不同弹性模型时结果的差异性[8]；Takuya 等[9]讨论了温敏凝胶-弹性基底复合结构的弯曲大变形特征；Arbabi 等[10-11]研究了pH 敏感凝胶-中性凝胶双层复合梁的弯曲行为，并给出解析解；Abdolahi 等则对温敏凝胶-不可压弹性体-温敏凝胶三层复合结构的弯曲行为展开研究，给出了曲率表达式。

本文则主要讨论光热敏感凝胶-橡胶双层复合梁的弯曲行为，利用光热敏感凝胶溶胀变形理论与梁弯曲理论推导相应的平衡方程、弯矩方程与应变协调方程，计算不同光强、温度条件下此类双层复合梁的曲率半径，分析弯曲变形规律。

1 理论模型

1.1 双层梁模型简介

本文研究的双层复合梁结构如图1 所示，下层为不可压橡胶，上层为光热敏感凝胶。 将该复合梁浸于溶液中，随着环境光强、温度的变化光热敏感凝胶层溶胀或收缩，而橡胶层体积保持不变。上、下层材料溶胀率的严重失配使得应力集中于复合梁的边缘，从而使得双层复合梁发生弯曲。 假设光热敏感凝胶层与橡胶层的初始厚度均为 1，初始宽度分别为 t10和 t20，初始长度为L0。

图1 光热敏感凝胶-橡胶复合梁示意图

1.2 光热敏感凝胶溶胀本构

在光辐射作用下，光热敏感凝胶吸收光能并转化为热能使凝胶温度升高，从而导致凝胶溶胀或收缩。 Toh 等[12]给出了光热敏感凝胶的本构方程

式中：SiK是作用于凝胶的名义应力；是凝胶的自由能密度函数；FiK为变形梯度；N 为凝胶网络链数密度；k 和T 分别为玻尔兹曼常数和凝胶感受到的温度；v是单个溶剂分子体积；J 为变形梯度第三不变量；I0为辐射光光强；hf 为单个光子的能量；分别为凝胶网络和溶剂的体积比热容；μs为溶剂化学势，而 χ0=A0+B0T 和 χ1=A1-B1T 为两个溶剂与凝胶网络相互作用参数，φ=1/J=1/（1+vCs）为聚合物体积分数；T=T0+ΔT=T0+αI0φ，T0为环境温度，ΔT 为光热转化增加的温度，α 为比例系数；A0,A1,B0和B1是4 个与凝胶种类相关的材料参数。

1.3 光热敏感凝胶-橡胶双层复合梁弯曲理论

如图2 所示，由于光热敏感凝胶层的溶胀以及橡胶层的不可溶胀作用，上下层的尺寸失配使得凝胶层与橡胶层间存在相互作用力[14]。 在相互作用力作用下，双层梁发生弯曲，如图3 所示。

如图2 所示，设凝胶层和橡胶层横截面间的相互作用力分别为F1和F2，由于无其他外力作用，因此可得

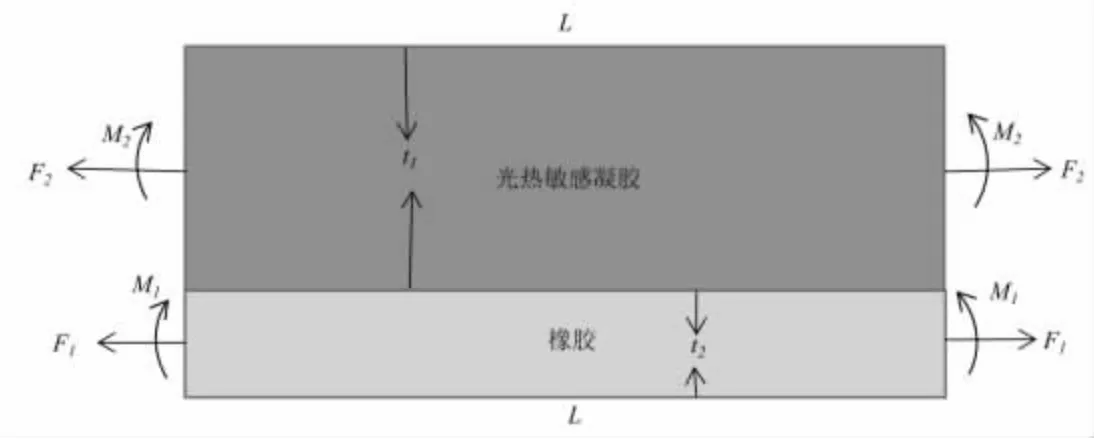
图2 凝胶-橡胶双层复合梁受力图

图3 双层梁弯曲示意图[13]

其中：M1和M2分别为作用于凝胶与橡胶横截面的弯矩； 而t1和t2分别为弯曲后的凝胶层和橡胶层的厚度，分别满足 t1=λ3t10，t2=t20，λ3为凝胶宽度方向溶胀比。

材料力学表明梁弯曲的曲率与弯矩成正比[13]，因此可得

其中：E1I1和E2I2分别为凝胶和橡胶的抗弯刚度；E1和E2分别为凝胶和橡胶的杨氏模量；I1和I2分别为凝胶和橡胶梁对弯曲中性轴的惯性矩，ρ 为曲率半径。

假设双层复合梁弯曲时其厚度的量级远小于其曲率半径，可近似认为凝胶层与橡胶层的曲率相等，因此，式（4）和式（5）简化为

由于凝胶的可溶胀性，其杨氏模量随凝胶的溶胀发生相应变化，因此，凝胶材料其弹性变形难易程度往往用增量模量表征[14]。 因此，凝胶梁的弯矩为：

而凝胶梁增量模量的计算方法如下。 在光辐射条件下，光热敏感凝胶溶胀，由于凝胶沿厚度方向无应力作用，由式(1)得

面内应力S1与面内溶胀率λ1的关系由本构方程（1）解得

将式(9)与式(10)联立得

因此，光热敏感凝胶增量模量为

假设凝胶层的最终厚度和宽度分别为λ1和t1=λ1t10，而橡胶层的厚度和宽度仍为1 和t2=t20，根据材料力学求得凝胶层和橡胶层对弯曲中性轴的惯性矩分别为：

界面处的应变协调条件为

其中：ρ 为双层复合梁的曲率半径。

将式(2)～(9)、(12)～(15)联立求得双层复合梁的曲率半径 ρ

其中，A 和 B 分别为

2 数值模拟

光热敏感凝胶在一定的光强、温度条件下预溶胀后粘附于橡胶层构成双层复合梁结构，随着光强、温度的改变，凝胶层继续溶胀或收缩使双层复合梁发生弯曲。 本节利用matlab 软件计算了不同预溶胀条件下光热敏感凝胶-橡胶双层复合梁的曲率半径随光强、温度变化关系，模拟用到的物理常数与材料参数如表1 所示。

表1 材料参数与物理常数[15]

2.1 光强的影响

图4 给出了温度T0为300 K，凝胶预溶胀率λ1分别为1, 2 和3 时双层复合梁的曲率半径ρ 随光强I0变化的关系曲线。 由图4 可见，温度一定，预溶胀率相同时，双层复合的曲率半径均随着光强的增大而增大。 这是由于温敏性水凝胶其平衡溶胀率随温度升高而降低，当环境光强越强时，因光热转化作用而获得的温升越高，温度越高凝胶吸收的溶剂越少。 凝胶的弹性模量与其含有的溶剂量有关，溶剂含量越低其弹性模量越大，凝胶材料则越硬越不容易变形。 因此，光强越强时，双层复合梁越不容易变形，其弯曲程度越小，曲率半径越大；预溶胀率越大时，光强相同的情况下曲率半径越小，双层复合梁弯曲程度越大，这是因为预溶胀率越大，凝胶材料初始含水率就越高，材料越软越容易发生变形。

2.2 温度的影响

图5 给出了光强I0=500 W, 凝胶预溶胀率I0分别为1, 2 和3 时双层复合梁的曲率半径ρ 随温度T0变化的关系曲线。 由图5 可见，双层复合梁的曲率半径随温度的增大先增大后减小，呈抛物线形状，曲率半径存在一个极大值。这可能与温敏性凝胶存在最低临界转变温度(LCST)有关。当温度在LCST 附近时，凝胶的溶胀率随温度升高发生突变式变化，凝胶急剧收缩使其弹性模量增大到一临界值，而温度高于LCST 后凝胶又缓慢溶胀。 由图5 还可以看出，预溶胀率越大，相同温度时双层复合梁的曲率半径越小，弯曲程度越大。

图4 温度T0=300 K时，不同预溶胀条件下双层复合梁的曲率半径ρ随光强I0 变化关系

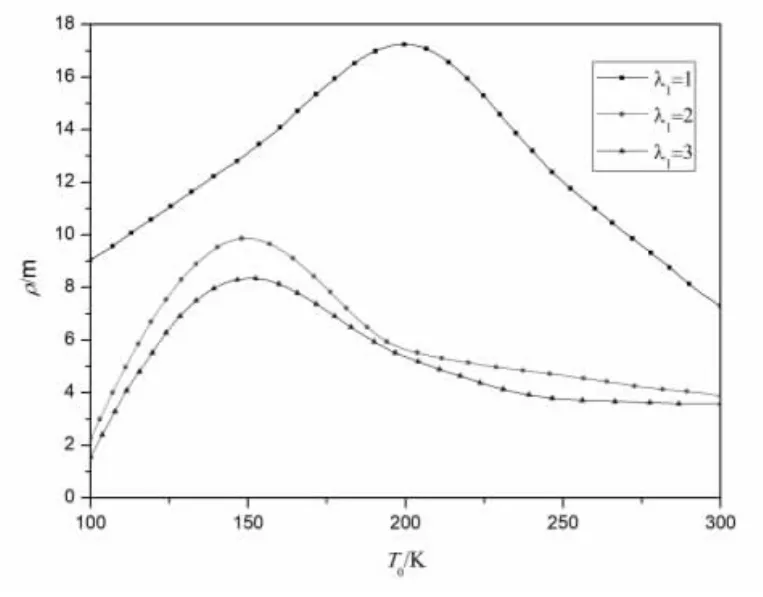
图5 不同预拉伸时曲率半径ρ随温度T0 变化关系曲线

3 结论

结合光热敏感凝胶溶胀大变形理论与梁弯曲理论推导了光热敏感凝胶-橡胶双层复合梁弯曲曲率半径的计算模型，并用matlab 进行计算，得到以下结论。

（1）光强对光热敏感凝胶-橡胶双层复合梁弯曲行为有很大影响，温度一定，预溶胀率相同时，双层复合的曲率半径均随着光强的增大而增大； 预溶胀率越大时，光强相同的情况下曲率半径越小，双层复合梁弯曲程度越大。

（2）双层复合梁的曲率半径随温度的增大呈抛物线变化关系，曲率半径存在一极大值。 这或许与光热敏感凝胶存在最低临界转变温度(LCST)有关，温度在LCST 附近时，随着温度的升高凝胶急剧收缩，温度高于LCST 后凝胶又缓慢溶胀。