基于T-S模糊的Delta算子时滞系统的H∞控制
2020-01-02王佑恩陈小翠
王佑恩,陈小翠
(三明学院 信息工程学院, 福建 三明 365004)
在实际生活中,随着工业过程的连续化、复杂化,诸多的控制系统都极其复杂,具有高度的非线性性、不确定性和时滞等特性,并且这些系统大都存在苛刻的约束和各种限制,使得一般的控制无法达到有效的控制。 时滞的存在却会给这些系统带来一系列不良因素,它的存在往往会导致系统性能降低以及系统不稳定,更甚引发系统故障的可能性增加。 而模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础,模拟人的近似推理和决策过程,所以模糊控制在处理不精确、控制具有高度不确定性的复杂系统时具有突出的优越性。 从E.H.Mamdani 在1974 年制造出用于锅炉和蒸汽机的第一个模糊控制器开始,直到Takeshi Yamakawa 倒立摆实验证明了模糊控制的应用后,模糊系统引起了大量的学者的关注,其中由Takagi 和Sugeno 提出的T-S 模糊系统在模糊系统是最活跃的一个分支[1]。 近几十年来,有关模糊系统和模糊控制方法的成果也越来越完善。 例如,文献[2]提出连续时间的模糊化和离散化;文献[3-4]研究模糊系统的输出反馈问题;文献[5-8]分析了非线性模糊系统的H∞稳定性问题、H∞滤波问题和H2/H∞采样控制;文献[9] 概述了T-S 模糊控制的研究现状,分析了保守性的问题。
1980 年中期,Middleton R 和Goodwin G 提出一种新的离散化描述方法——Delta 算子方法[10]。近十几年以来,在对Delta 算子系统研究的不断加深的过程中,研究这方面问题的学者们讨论了一系列的控制问题,包括了系统的稳定性[10]、滤波问题[11]和容错控制[12]、保性能控制[13]、H∞控制[14]等控制问题。
本文针对模糊Delta 算子描述的范数有界不确定时滞系统,设计一个具有H∞性能的状态反馈控制器的控制问题。 假设系统含有运用Lyapunov 稳定性理论,将控制问题化为线性不等式矩阵问题,由此给出满足H∞性能指标γ 的状态反馈控制器的存在条件和设计方法,然后通过Matlab 的工具箱LMI 解得状态反馈控制器Kj,j=1,2,…,p。 最后通过数值计算,验证了该方法的可行性。
1 问题描述
考虑下列 T-S 模糊 Delta 算子时滞系统,并且该系统是非线性的,如果 θ1(tk)是 Ni1,且 θ2(tk)是Ni2,…,且 θp(tk)是 Nip,则

这里 i 是被控对象原则,Nij(θ(tk))表示隶属度,且Delta 算子表示为系统状态向量 x(tk)是 n 维的,系统控制输入 u(tk)是 m 维的,w(tk)为外部扰动,h,dk分别表示采样周期和系统时滞,且假设 0<dk<d*(d*是已知正整数),Ai,Adi,Bi,Bli,Ci是常数矩阵,假设系统的不确定性矩阵ΔAi,ΔAdi满足范数有界,即

式中:M、Ei、Edi为已知适维常数矩阵,F 为满足FTF≤I 的适维不确定性参数矩阵。 基于并行分布式补偿原理,建立如下的模糊状态反馈控制器 j:如果是 θ1(tk)是 Ni1,且 θ2(tk)是 Ni2,…且 θp(tk)是Nip。

基于以上假设,T-S 模糊Delta 算子时滞系统(1)可以重写为

和控制器模型(3)可以写成如下形式

这样,将(5)式代入(4)中,得到模糊Delta 算子时滞闭环系统

定义 1[15]对给定的正常数 γ,如果闭环系统(5)具有以下性质
(1) 闭环系统是渐近稳定的;
(2) 在零初始条件(x(tk)=0,k<0)下,‖z‖2< γ‖w‖2,∀w∈L2[0,∞)。则称闭环系统(5)具有给定的H∞性能γ。
本文的主要研究模糊Delta 算子时滞系统(1)的H∞控制问题。 考虑T-S 模糊性,应用Lyapunov稳定性理论,设计一个状态反馈控制器(4),无论系统含有时滞现象和不确定矩阵F,都使得闭环系统(5)渐近稳定,且闭环系统具有H∞性能γ。
2 主要结果
为了使得闭环系统(5)渐近稳定,需寻找一个状态反馈控制律Kj,从而提出相应的设计方法.在这之前,首先介绍以下两个引理。
引理 1[15]给定适维矩阵 Y、D 和 F,其中 Y 是对称的,则 Y+DEF+ETFTDT<0 对所有满足 FTF≤I的矩阵 F 成立,当且仅当存在一个常数 ε>0,使得 Y+εDDT+ε-1ETE<0。
引理 2[15](Schur 补性质)设对称矩阵其中 S11是 r×r 的,以下 3 个条件等价
(1) S <0;
应用Lyapunov 理论,结合引理1 和引理2,得到本文的主要结论。
定理 1基于 T-S 模糊,对 Delta 算子时滞不确定系统(1),在给定 γ(γ>0)的情况下,若存在对称正定矩阵P,S,使得对系统时滞dk和所有的不确定矩阵F,下列矩阵不等式

成立,则模糊 Delta 算子时滞系统(1)存在一个状态反馈控制器 u(tk)= Kjx(tk)使得闭环系统渐近稳定,且满足H∞性能γ。
首先,假设 w(tk)=0 条件下,有


另一方面

由(8)和(9)式得

由(6)式可知,Ωij<0,从而 δV(tk)<0。 由 δ 域 Lyapunov 稳定性理论,闭环系统(5)是渐近稳定的。
进一步对任意非零 ‖z‖2< ‖w‖2,∀z∈L2[0,∞),由(9)和(10)式有

根据引理 2 可得:(6)式成立等价于 Φij<0,从而由(13)式可得

由初始条件,(14)式两边同时由0 到N 求和得

由等式 w(tk)∈L2(0,∞),即可得到‖z(tk)‖≤ γ‖w(tk)‖,则闭环系统(6)具有给定的 H∞性能γ。 定理得证。
由于矩阵不等式 (6) 是非线性的, 接下来将其转化为先行矩阵不等式, 从而利用线性矩阵不等式刻画给出系统(1)控制律的存在条件,并由此线性矩阵不等式的可行解给出H∞控制律的构造方法。
目前,对同步交流发电机旋转整流器进行故障诊断的方法主要有励磁电流分析法[3]和输出电压分析法[4]。其中,励磁电流分析法通过采集同步交流发电机励磁机励磁电流,对其进行傅里叶变换提取相关特征,并进行故障诊断[5],而输出电压分析法则采集同步交流发电机三相输出电压信号,对其进行小波变换并获取相关特征参数,从而实施故障诊断操作[6]。此外,亦可以利用旋转整流器整流电压进行傅里叶变换或者小波变换以提取故障特征,从而进行故障诊断操作[7]。因此,利用傅里叶变换法或小波变换法处理相关信号,均能提取相关故障特征参数,并实施同步交流发电机旋转整流器的故障诊断。
定理2基于T-S 模糊,对Delta 算子时滞不确定系统(1),如果存在标量ε>0, 矩阵W,对称正定矩阵使得下列不等式

成立, 那么模糊 Delta 算子时滞系统(1)存在状态反馈控制器使得闭环系统(5)渐近稳定,并且具有H∞性能γ。
证明 由定理1 成立, 即(6)式成立, 则模糊Delta 算子时滞系统(1)存在状态反馈控制器。 现将和(2)式代入(6)式得

根据引理1, 上式成立当且仅当, 存在一个整数ε 使得

成立。 根据引理2, (14)式等价于

对(15)式左右两边同时乘矩阵 diag{P-1, I,P-1,I,I,I,εI}再根据引理 2 得:

3 数值算例
为了验证所提方法的可行性, 考虑倒立摆平衡问题, 变量假设如下:摆与垂直方向的夹角为x1,角速度维x2, 重力加速度为g=9.8 m/s2, 摆的质量m=2 kg,滑车的质量M=8 kg,摆的长度2l=1 m,滑车上的作用力u,外部扰动变量w, 所以摆动方程[16]为
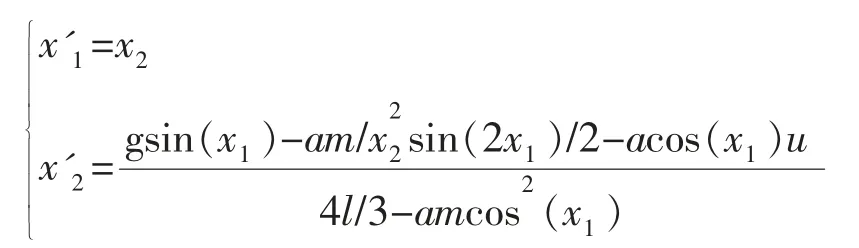
基于以上假设, 得到下面T-S 模糊Delta 算子时滞系统


令采样周期h=0.1,性能γ=1,外部扰动w(tk)=sin2tk,系统时滞上界。应用MATLAB 求解线性矩阵不等式(11),解得

所以模糊Delta 算子时滞系统(1)的鲁棒H∞控制的状态反馈控制律为

4 结语
本文在运用李雅普诺夫理论和LMI 方法的基础上,研究T-S 模糊Delta 算子时滞系统的控制问题,将控制问题转化为线性矩阵不等式的可行解问题,从而给出状态反馈控制器存在的条件和控制器设计方法,证明闭环系统是渐近稳定的,且具有给定的性能.
