横向紊流风中移动车辆纵向风速谱分析
2020-01-02段青松吴再新李建兴马存明
段青松,吴再新,李建兴,马存明
(1.四川省铁路产业投资集团有限责任公司,四川成都 610094;2.西南交通大学土木工程学院,四川成都 610041)
中国是世界上少有的几个受风灾较严重的国家,轻微的风灾可能会引起车辆的限速,影响车辆的运输能力,严重的风灾可能会造成车辆停运、晚点,甚至引发安全事故。车辆在横风作用下的安全性问题引起了广大学者的关注,必须采取措施避免此类事故的发生[1-3]。在横向紊流风作用下,移动车辆的风速谱可能会发生变化,进而引起风荷载特性的改变。因此,对移动车辆风速谱特性的研究可为准确模拟车辆风荷载打下良好的基础。
国内外的学者对移动车辆的风速谱特性进行了研究。Cooper[4]在 1984年首先通过“Taylor 冻结假设”基于von Kármán 谱推导了来流横风垂直于移动车辆运行方向时的移动车辆纵向风速谱,该风速谱的推导得到了许多学者的认可,并作为进一步分析风-车-桥耦合作用的基础,但是该推导只针对横向紊流风与移动车辆垂直时的工况。吴梦雪[5]利用Cooper的相关理论通过数学表达式的方式给出了基于Simu 谱的移动点风速谱表达式,但是该解析式的形式过于复杂,不便于应用。为了解决这一难题,李小珍等[6]通过解析表达式的形式给出了基于Cooper 理论的Simu 谱和von Kármán 谱的移动车辆风速谱,认为移动车辆风速谱存在多普勒效应。吴梦雪和李小珍与Cooper 对移动点的风速谱推导均是利用“Taylor 冻结假设”,但与Cooper 不同的是二者均忽略了车辆移动引起的紊流积分尺度的变化。不依赖于传统的“Taylor 冻结假设”和各向同性紊流假设,胡朋等[7]在谐波合成法的基础上提出了一种“直接生成法”并验证了其有效性。Watkins 等[8]通过现场实测试验分析了移动车辆引起的风场紊流强度的变化。目前,对移动车辆风速谱特性相关变化规律的理解尚未进行总结归纳,有待进一步加强。
本文在上述研究的基础上,基于Cooper 移动车辆风速谱理论给出移动车辆风速谱的解析表达式,并分析风偏角、风速与车速比值等因素对移动车辆风速谱峰值及其对应频率的缩放系数的影响。首先,给出静止点von Kármán 谱以及移动车辆风速谱的解析表达式;然后,通过风洞试验模拟紊流场;最后,推导模拟紊流场对应的移动点风速谱,并对其相关特征展开分析。
1 移动点风速谱推导
1.1 静止点风速谱推导
紊流的相关性可以用速度的相关函数f(r)和g(r)来表示。f(r)是相距r的空间2 点的速度分量在轴线方向的互相关函数(图1(a)),g(r)是相距r的空间2点的速度分量在垂直于轴线方向的互相关函数(图1(b))。具体定义如下:
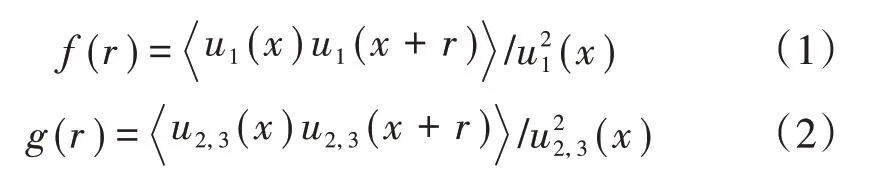
式中:u1,u2,u3为空间某点在x,y,z方向的脉动风速。
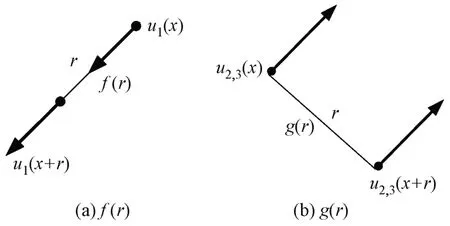
图1 互相关函数
纵向和竖向的紊流功率谱密度函数分别为
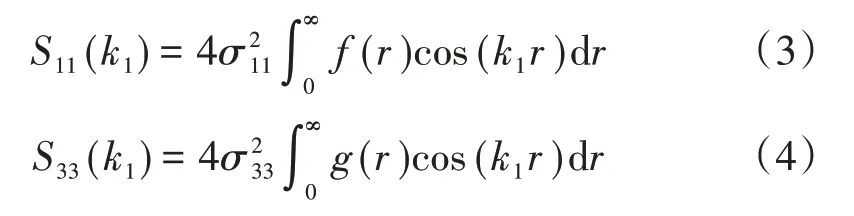
式中:σ11和σ33均为脉动分量的均方根值为来流平均速度,f为频率。
在三维紊流理论中,紊流积分尺度可通过对相关函数的积分得到,即

von Kármán[9]根据球对称假设推导了g(r)与f(r)之间的关系,为
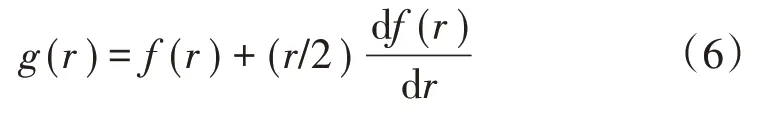
式(5)可以表达为
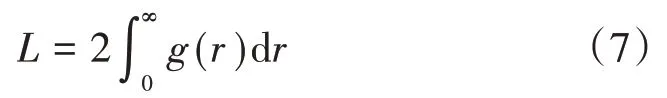
Bullen 基于各向同性紊流理论,推导了互相关函数的数学模型,即
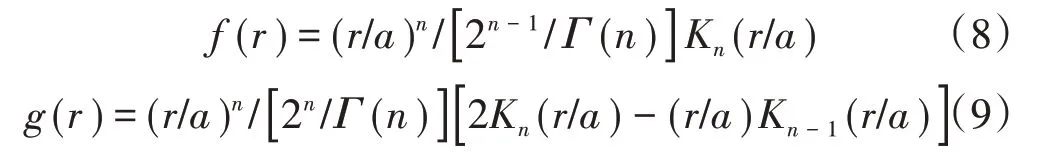
式中:a和n分别为控制形状和尺度的参数;Kn和Kn-1为第二类型贝塞尔函数;Γ为Gamma函数。
各向同性紊流中,紊流积分尺度L与参数a之间满足如下关系:
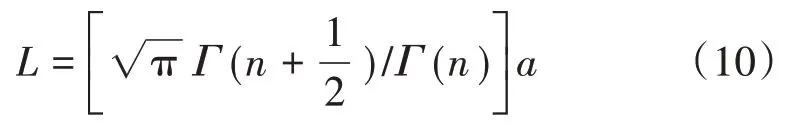
将式(8)、式(9)分别代入式(3)、式(4),可得
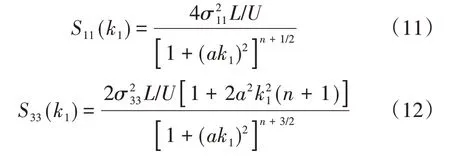
当n=3/2时,可得到von Kármán谱[10]:
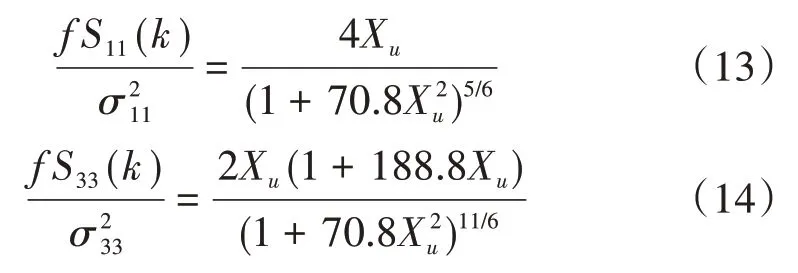
式中,Xu=k1L/(2π)。
1.2 移动点风速谱推导
大多数文献研究的风速谱主要是考虑空间某一静止点的风速谱,未考虑移动点在来流紊流场中的风速谱。高速铁路车辆等多处于运动状态,有必要分析移动点的风速谱,便于进一步分析移动车辆的相关特性。
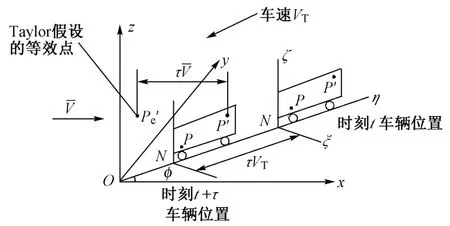
图2 移动车辆上固定2点与等效点示意
根据“Taylor冻结假设”,可将时间延迟τ转变为等价的空间间隔因此,相应于物理点P′(时刻t+τ),在“冻结”紊流场(时刻t)中有对应的等效点。随着车辆一起运动的点P和点P′的紊流互相关性就等价为“冻结”紊流场中的点P和点的紊流互相关性。
在图2中,“冻结”紊流场中的点P和点之间的等效间隔在x,y,z轴上的投影距离分别为
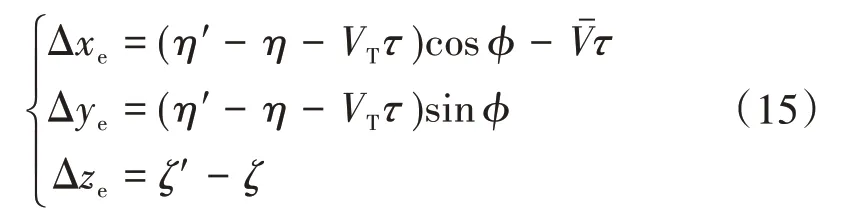
根据以上分析可知,运动车辆上固定2 点之间的紊流互相关函数可以表示为
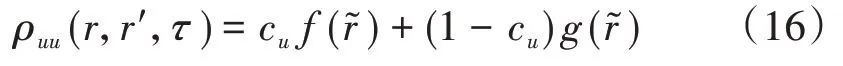
当点P和点P′重合时,式(15)变为
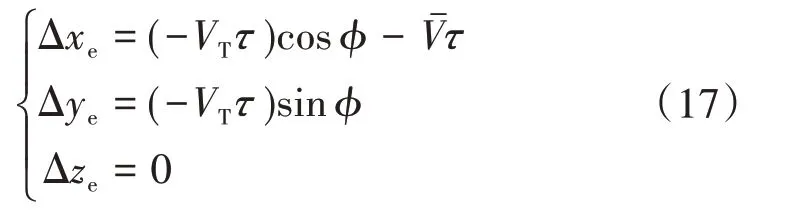
移动单点的紊流自相关函数通过傅里叶变换可得紊流功率谱密度函数,为
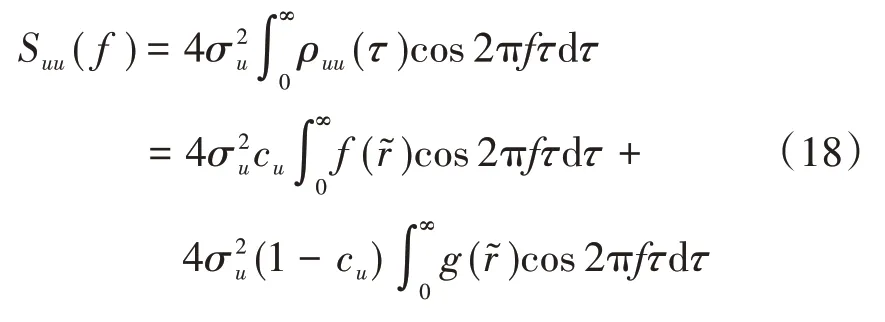
式中,σu为脉动速度的均方差。
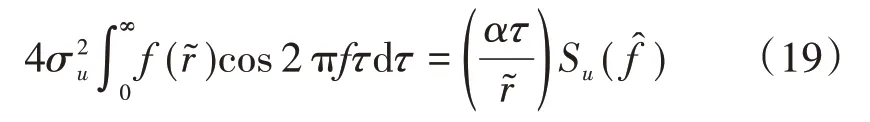
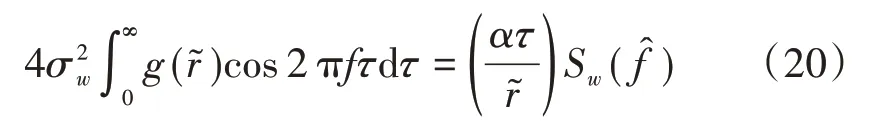
将式(19)与式(20)带入式(18),可得
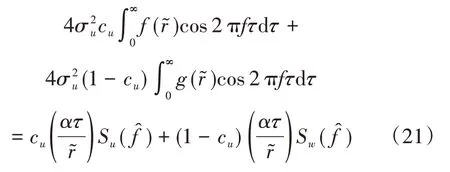
对于von Kármán 紊流风速谱模型,α=0.747。某一移动点的自相关及功率谱密度函数的相关参数分别为
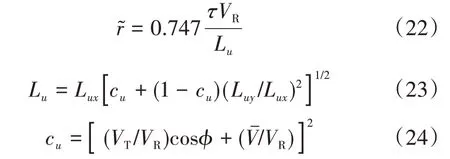
对应于静止点风速谱为von Kármán 谱的移动点风速谱可表示为
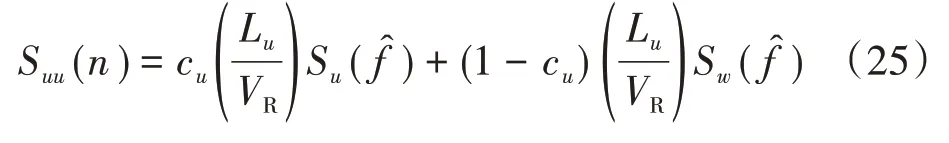
因此,基于Cooper 关于移动车辆功率谱密度函数的理论以及静止风速谱的理论推导过程,可以得到移动点风速谱的通用公式,同时可以得到纵向谱为von Kármán 谱对应的移动点风速谱。移动点横向风速谱的推导与纵向脉动风速谱类似,二者结果的不同主要与ci(i=u,v),Lu及VR有关。本文只针对移动点的纵向风速谱进行分析。
为了验证本文推导过程的正确性,图3给出了车速分别为0,10 m/s,纵向积分尺度为45 m,来流风方向垂直于列车运行方向时,推导结果与Cooper 结果的对比曲线。图中横坐标轴为对数坐标,纵坐标轴为线性坐标。可知,推导结果与Cooper 的结果吻合较好,证明了本文推导过程的正确性。
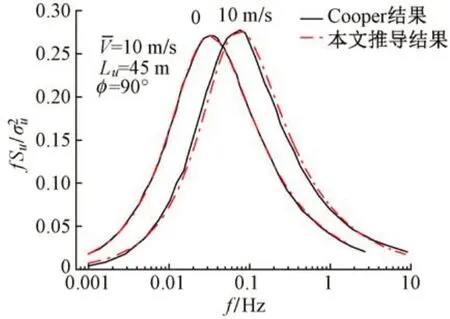
图3 基于von Kármán谱的移动点脉动风速谱对比曲线
2 移动点风速谱特性分析
在西南交通大学XNJD-3 风洞实验室进行紊流场模拟。采用TFI 眼镜蛇三维脉动风速测量仪(Cobra Probe)。紊流场布置为:尖塔在风速入口处前方,并排放置13 个,间距为1.6 m,尖塔底部宽为0.5 m,高为4.3 m,尖塔的具体尺寸见图4。紊流风的采集频率为512 Hz,采集时间为180 s。
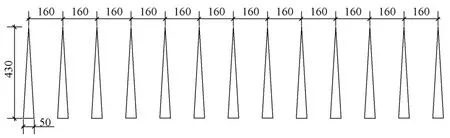
图4 紊流风场试验的布置(单位:cm)
试验前需检验风洞中的风场特性均匀性。在距尖塔水平2.5 m,距地面竖向1.0 m 处,沿横向和纵向对各测点的紊流风特性进行多次测量。结果显示2种紊流场的风特性在空间位置变化很小,风场的均匀性良好,完全满足试验的要求。紊流场风速谱与von Kármán 谱对比见图5。可知,二者吻合较好,基本满足水平各向同性假设。
尖塔紊流场主要紊流特性见表1。将表1中参数带入式(25),即可得到移动点风速谱结果。
图6给出了风偏角ϕ=15°~175°时,试验模拟紊流场的静止点风速谱对应的移动点风速谱结果,车速与风速比值为0~5。当车速为0 时,即为尖塔紊流场的静止点风速谱。移动点风速谱中的积分尺度采用表1中的数值。
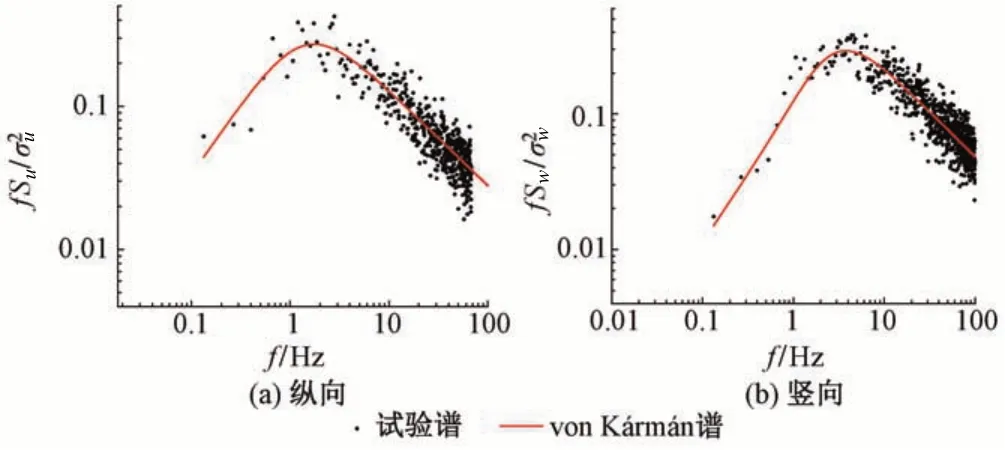
图5 紊流场风速谱与von Kármán谱对比

表1 尖塔紊流场主要紊流特性
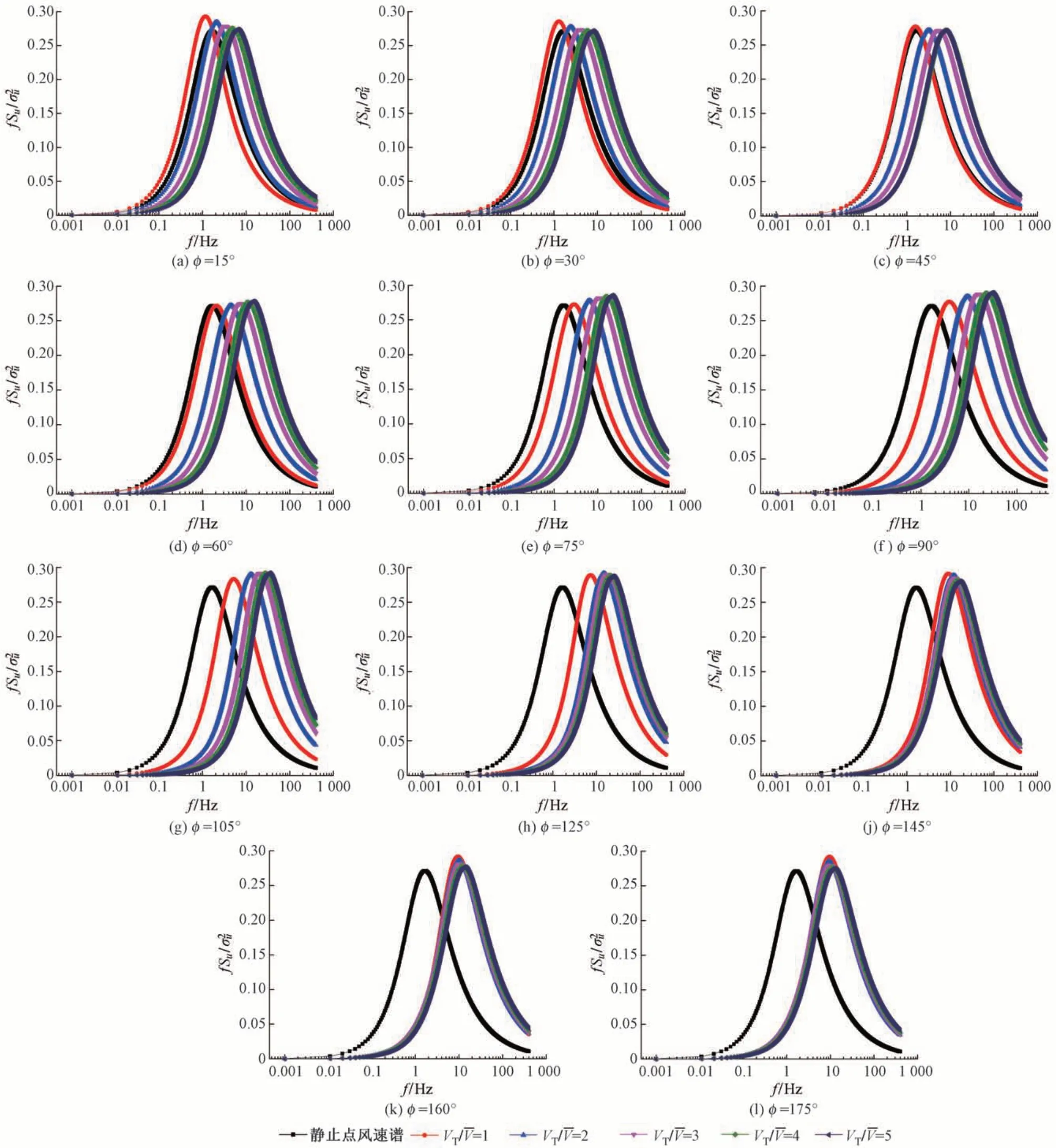
图6 不同风偏角与车速时移动车辆风速谱
由图6可知:
2)当ϕ=15°~30°时,随着不断增大,移动点风速谱峰值逐渐减小,当分别为4 和5 时,移动点风速谱峰值基本相同。当ϕ=45°时,不同下移动点风速谱峰值逐渐接近;当ϕ=60°时,不同下移动点风速谱峰值基本一致。风偏角继续增大,随着不断增大,移动点风速谱峰值逐渐增大;当风偏角分别为160°和175°时,不同下移动点风速谱基本重合,但随着不断增大,风速谱峰值逐渐减小。
3 移动点风速谱峰值特征分析
为了进一步分析车速与风速比值、风偏角对移动点风速谱的影响,图7给出了在不同风偏角及时的移动点风速谱峰值放大系数。其中,放大系数为移动点风速谱峰值与静止点风速谱峰值的比值,移动点、静止点风速谱峰值及其对应的频率可从图6中提取。
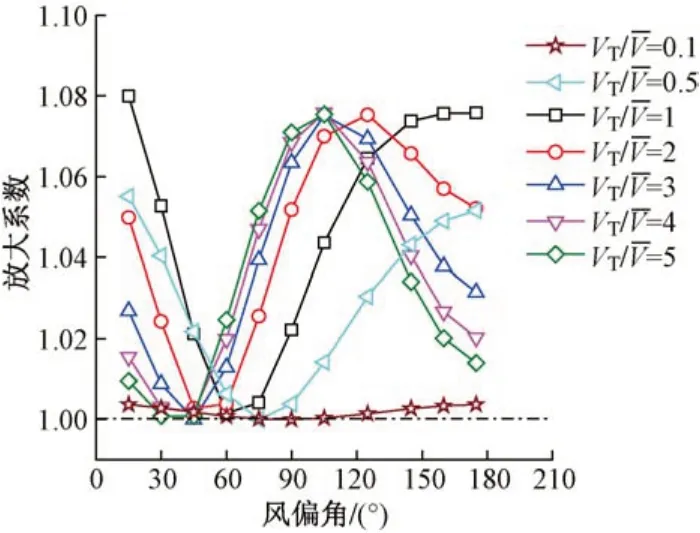
图7 移动点风速谱峰值放大系数
由图7可知:
1)移动点风速谱峰值比静止点风速谱峰值大;随着风偏角增大,移动点风速谱峰值可分为3个区域,即逐渐减小区域I,逐渐增大区域Ⅱ和逐渐减小区域Ⅲ;随着增大,放大系数的最大值与最小值对应的风偏角基本不变。
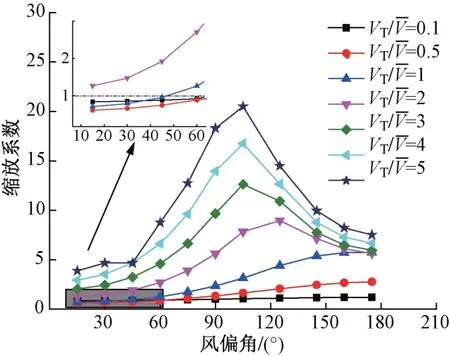
图8 移动点风速谱峰值对应频率的缩放系数
4 结论
1)利用Taylor 冻结假设,基于静止点纵向风速谱von Kármán 谱解析得到了移动车辆风速谱,并验证了推导公式的可行性与正确性。
2)在风洞实验室模拟了与von Kármán 谱吻合较好的大气紊流场,得到了不同风偏角、车速与风速比值时的移动车辆风速谱。
