一种时间序列鉴别性特征字典构建算法∗

(北京交通大学 计算机与信息技术学院,北京 100044)

时间序列是一系列按时间进行排序的实值数据组成的集合.在许多研究领域或实际应用领域之中存在着大量的时间序列数据,例如恶意软件检测、风能预测、工业自动化、电压稳定评估、移动设备追踪等领域[1-3].目前,获得的时间序列通常具有如下两个特点:时间序列数据集的规模很大,同时,每条时间序列数据的维度都很高.

时间序列分类(time series classification,简称TSC)技术的研究涉及到许多方面的技术问题,这些问题可能包括时间序列特征的发现或生成以及如何存储或压缩时间序列等.Esling 等人对时间序列的研究领域给出了详细介绍[4].Bagnall 等人对各种时间序列分类算法进行了详细分析[5].一般TSC 算法可大致分为两类:基于完整时间序列的方法和基于局部特征的方法[6].前者基于全局相似性进行分类预测,主要研究相似性的不同度量方式和使用方法[7-11];而后者基于时间序列的局部特征进行分类预测,通常利用不同的特征生成和转换技术来发现局部特征,然后基于建立的特征集合直接构建分类模型或对时间序列数据进行转换[12-15].然而,目前多数的TSC算法无法以足够的精度和速度充分处理大规模的数据.一些精度较高的分类算法,例如,基于局部鉴别性特征Shapelet 的转换算法的时间复杂度为O(N2×n4)[16],其中,N为时间序列数据集中的实例数,n为时间序列的长度.基于时间序列转换的集成分类算法(the collective of transformation-based ensembles,简称COTE)[17]的分类精度显著地优于常见的时间序列分类算法,但该算法中包含多个时间复杂度非常高的基分类器.

为了提高TSC 算法的分类效率,时间序列的快速转换表示方法成为当前的一个研究热点.本文对基于特征包(bag-of-pattern,简称BOP)的分类模型进行研究,这类模型具有分类精度高和运行速度快的特点.BOP 模型将时间序列分成一系列子结构,并将这些子结构作为离散化特征构建特征字典,最后将基于特征频数的向量作为模型训练和分类的基础.最早的特征包模型(bag-of-patterns using symbolic aggregate approximation,简称BOPSAX)[18]使用固定长度的滑动窗口和符号聚合近似技术(SAX)将每个窗口中的子序列转换成离散化特征,然后使用基于频数向量的欧几里德距离作为相似性度量方式,最后通过1NN 分类器进行分类预测.Senin 等人利用SAX 技术和向量空间模型构建了一种新的时间序列分类模型(symbolic aggregate approximation and vector space model,简称SAX-VSM)[19],该模型基于词频-逆向文档频率(term frequency-inverse document frequency,简称tf-idf)对符号化特征进行加权,同时使用余弦距离代替欧式距离进行相似性度量;此外,它只为每个类构建一个特征向量,而不是每个样本一个向量,这极大地缩短了模型的运行时间.Neuyen 等人[14]对基于SAX 的转换方法的可变长度的单词进行了研究,并将序列学习算法用于转换后的时间序列分类问题.SAX 技术本质上仍然是在时域空间对时间序列进行处理,然而,实际中的一些问题在时域空间进行处理时会比较困难,而在频域空间更容易取得好的处理效果.例如,通常可在频域空间将代表噪声的频率成分去除来实现降噪.此外,频域中包含一些时域难以发现的鉴别性信息.

离散傅里叶变换(discrete Fourier transform,简称DFT)[20,21]可将时域空间的时间序列转换为一组频域空间的不同频率的正弦波.因此,基于离散傅里叶变换的时间序列符号化表示方法受到各国研究人员的重视.Schafer等人[22]提出用符号傅里叶近似(symbolic Fourier approximation,简称SFA)来代替SAX 对时间序列进行离散化表示.接着,Schafer 又提出了一种基于SFA 的特征包算法(bag-of-SFA-symbol,简称BOSS)[23],但该算法对时间序列离散化过程中只简单挑选前l个傅里叶值,未考虑傅里叶值的鉴别性.为此,Schafer 等人进一步提出一种用于时间序列的单词抽取方法(word extraction for time series classification,简称WEASEL)[24],该方法用鉴别性较强的top-l个傅里叶值代替前l个傅里叶值对时间序列进行符号化,但是该方法存在一个明显的缺陷,其将所有长度子序列转化得到的单词设为定长,即,所有子序列经离散傅里叶变换后保留的傅里叶值的个数相同.然而,实际中不同周期的时间序列子序列所含有的鉴别性频域信息量可能不同,单一的固定长度会导致损失大量鉴别性信息或包含冗余信息.为此,针对目前基于SFA 的时间序列离散化表示方法存在的问题,本文首先提出一种用于时间序列分类的基于SFA 的可变长度单词抽取算法(variable-length word extraction algorithm,简称VLWEA).该算法为每个窗口长度学习性能最优的单词长度.图1 展示了本文提出的变长单词抽取算法相对于定长单词抽取算法所具有的优势.图中,w表示滑动窗口长度,lw表示长度为w的滑动窗口中提取的单词长度,c1和c2表示类别.

图1(b)中给出了长度为6 和8 的滑动窗口获得的4 个子序列经过SFA 转换得来的完整字符序列.图1(a)所示为用定长单词抽取算法得到的特征(假定共同单词长度为4),其中,“6aabc”表示一个长度为6 的滑动窗口子序列抽取出的长为4 的字符序列,即特征.图1(c)中给出了变长单词抽取算法获得的两种长度滑动窗口对应的特征,变长单词抽取算法旨在获得具有更强鉴别性的子序列.从图1 可以看出,定长单词“8abab”无法区分长为8的两类子序列,而变长单词“8ababc”和“8ababd”可区分两类子序列.此外,定长单词“6aabc”和“6acbc”虽可区分长度为6 的两类子序列,但与变长单词“6aa”“6ac”相比,包含了更多的冗余成分.

与此同时,针对基于VLWEA 建立的特征字典中存在大量冗余特征的问题,本文基于tf-idf 的基本思想定义了一种新的特征鉴别性强弱度量方式来对鉴别性特征进行选择,并能根据不同周期生成的特征的整体分类性能动态设定各周期生成特征的选择阈值.本文的主要贡献概括如下.

(1)本文提出了一种基于网格搜索的滑动窗口单词长度学习算法.该算法为不同窗口长度学习分类性能最优的单词长度,不同窗口长度可能生成不同长度的单词.变长单词可有效减少鉴别性信息的损失,在此基础上可以获得更优的分类效果.与此同时,我们分析了Bigrams 语法模型对基于变长单词特征字典的模型分类性能的影响.

(2)本文基于tf-idf 的基本思想定义了一种新的特征鉴别性评价统计量用于特征选择.

(3)针对采用固定阈值进行特征选择忽略了不同周期转换得来的特征存在性能差异的问题,我们提出一种根据不同滑动窗口生成特征的整体分类性能以动态地设定各窗口生成特征选择阈值的机制,该机制可有效缩小时间序列特征空间的规模并提高模型的分类性能.

本文第1 节介绍基本概念和理论基础.第2 节介绍本文使用的相关算法.第3 节给出实验方式和实验结果.第4 节总结全文.

1 定义与理论基础

本节介绍时间序列的基本概念和基于SFA 的时间序列转换表示方法的理论基础.

1.1 时间序列

下面我们首先介绍本文用到的一些基本概念.

定义1(时间序列).时间序列T是由n个有序的实际观测值t0,t1,…,tn-1组成的一个实值序列,即T={t0,t1,…,tn-1},其中,ti∈R.

用D={T0,T2,…,TN-1}表示包含N条时间序列的数据集合,其中,每条时间序列Ti={ti1,ti2,…,tin}.

定义2(时间序列子序列).给定一条完整的时间序列T={t0,t1,…,tn-1},该序列T中长为ω的窗口S之中包含的ω个连续值组成的序列称为时间序列T的子序列,若其在时间序列T上的起始位置为a,则S(a,ω)=(ta,ta+1,…,ta+ω–1),其中,0≤a≤n-ω.

定义3(特征字典).特征字典是用于表示时间序列数据的特征集合.

本文构建的特征字典中的每个元素为一个指定长度滑动窗口生成的字符序列.表1 给出文中涉及的常用符号.

1.2 时间序列离散傅里叶变换

本节我们介绍时间序列的离散傅里叶变换过程[20,21].

给定一条由n个数值组成的离散序列T={t0,t1,…,tn-1},其离散傅里叶变换公式为

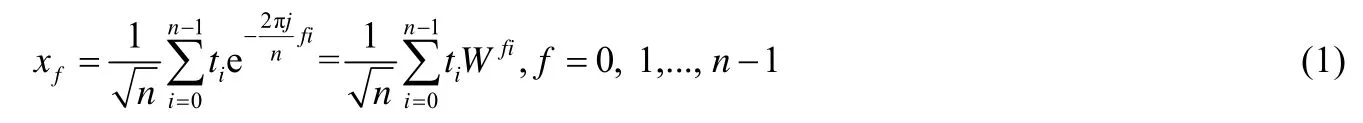
其中,j为虚数单位,即,W 为

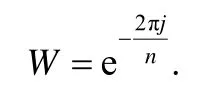
经公式(1)可将离散数值序列T转换为序列x,转换过程可表示为

上式可简单记作:

其中,F称为离散傅里叶变换矩阵.

矩阵F中第i行表示第i个正弦波,xi表示时间序列在这个正弦波上的投影,即,时间序列T中包含的第i个频率正弦波成分的多少.它反映了时间序列与该频率正弦波的相关性.

数据x={x0,x1,…,xn-1}为经离散傅里叶变换得到的数据,称为频域向量.时间序列T可通过逆变换来恢复,即,

其中,FH表示正交矩阵F的共轭转置.

定理1(Parseval theorem)[25].若x为序列T经离散傅里叶变换得到的序列,则有

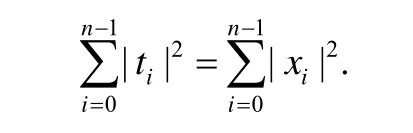
上述定理说明序列T在时域空间的能量与在频域空间的能量相同.

时间序列的每个元素可以表示为

复数xf通常称作傅里叶系数(Fourier coefficient).

通过欧拉公式可以将公式(1)表示为

傅里叶系数xf可分为realf实数部分和imagf虚数部分:

经过傅里叶变换,我们得到的傅里叶系数值序列可以表示为

由于realn-f=realf,imagn–f=-imagf,imag0=0,所以上述2n维数组可用n维数组表示.

当n为偶数时,imagn/2=0,x可以表示为

当n为奇数时,x可以表示为

考虑到傅里叶值的对称性,为了减少计算量和存储空间,一般用n维数组对傅里叶值进行存储.由于x中的傅里叶值代表了固定周期内的时间序列的频率成分,因此,符号傅里叶的近似过程就是对这些傅里叶值进行选择和符号化转换.下面我们介绍基于SFA 的特征生成过程.

1.3 基于SFA的特征生成

基于SFA 的特征生成过程分为两步:首先,从子序列转换得到的傅里叶值数组中选择鉴别性最强的top-l个傅里叶值;其次,利用分箱技术将选择的傅里叶值依序转换为符号组成单词,即,特征.

傅里叶值的鉴别性度量本质上是根据一系列标定类属性的实值来判断这组值对应的频率成分的鉴别性强弱.Schafer 等人[24]提出利用F统计量对傅里叶值的鉴别性强弱进行度量,然后选择鉴别性最强的前l个傅里叶值.这样处理比简单挑选top-l个傅里叶值生成的特征更具有鉴别性.本文我们也使用F统计量进行傅里叶值鉴别性度量,与Schafer 所提方法不同的是,我们为每个窗口长度选择分类性能最优的傅里叶值个数进行特征生成,而Schafer 等人使用的方法所有滑动窗口都选择鉴别性top-l个傅里叶值.计算reali或imagj对应的实数集上的F统计量的类内方差MSW和类间方差MSB的计算公式[24]为

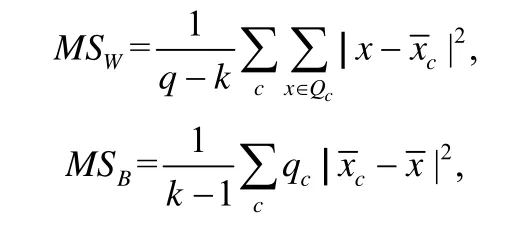
其中,Q为reali或imagj对应的傅里叶值集合,q为集合Q中实数的个数,k为集合Q中的类属性取值个数,x为集合Q中的任意实数.Qc为集合Q中类属性值为c的傅里叶数值集合,qc为集合Qc中实数的个数,为集合Q中所有实数的均值,为Qc中所有实数的均值.

F值的计算公式为

当F值用于傅里叶值选择时,我们希望找到最大的F值,其等价于不同类均值之间的最大差,此时,傅里叶值的鉴别性最强.

例如,给定一个长为10 的子序列,假设我们选择的前4 个傅里叶值为“0.11,0.23,0.02,0.63”,利用分箱技术我们可将该实值序列转换成为一个字符序列,假设为“abcd”,由于不同长度的滑动窗口代表不同周期的频率成分,它们生成的特征不同,为此,每个单词都对应固定的滑动窗口长度,上述生成的单词通常表示为“10abcd”.Schafer在文献[23]中对SFA 的具体符号化过程进行了详细介绍,这里不再赘述.

n0元语法模型(n0-gram)是自然语言处理中很重要的统计语言模型.该模型在实际应用中通常假设某个词出现的概率只与它前面的一个或几个词有关,即,马尔可夫假设.当n0=i时(i为正整数),称为i元语法,也称为i阶马尔可夫链,此时第j个词出现的概率只与其前i-1 个词有关.n0取1、2 和3 时,基于n0元语法表示获得的词组称为一元单词(unigram word)、二元单词(bigram word)和三元单词(trigram word).此外,若特征字典有m个特征,则基于n0元语法要考虑的词组合可能有个.因此,为了缩小特征字典的规模,通常只考虑一元和二元词组组成的特征.为了弥补所有周期抽取定长单词所导致的鉴别性信息的损失,Schafer 等人[24]将n0元语法用于时间序列的特征构建过程中,他们将连续出现的两个特征组成一个新的特征加入到特征字典.本文将一元和二元语法模型分别记为Unigram 和Bigrams,并对Bigrams 语法模型对变长单词特征字典的性能影响进行了实验分析.

1.4 特征的鉴别性评价

tf-idf 是一种用于寻找文本中关键词的统计方法[26,27].它通常用来评估一个词与一篇文档的主题的相关程度.词对一篇文档的重要性与其在该文档中出现的频率成正比关系,同时,与其在语料库中出现的频率成反比.如果某个词在所有的文档中都出现,则意味着与主题并不相关.本文基于tf-idf 的基本思想设计了一种新的tfidf 统计量对特征的鉴别性进行评价.新定义的鉴别性评价指标主要从两个方面对各类特征的鉴别性进行评价.

(1)某类特征和该类的相关程度.主要通过tf 值来度量,我们用某类特征在该类所有实例中的出现频率来度量该特征和所属类别的相关性.

(2)某类特征对该类的鉴别性强弱.实际中,某类中高频特征也可能是其他类中的常见特征.此时,该特征不能有效区分不同类别.为此,我们用idf 度量该特征对所属类别的鉴别性强弱.

下面首先对本文定义的tf-idf 计算公式进行介绍.我们用特征在某类中出现的相对频率代替其在某个实例中出现的频率以衡量它与某类实例的相关程度.我们用f(t,c)表示特征t在其类属性c对应的实例集合中出现的次数,即,类属性为c的特征t在类属性为c的所有实例中出现的次数总和.特征t在其类属性c对应的特征字典中的频率tf(t,c)的计算公式为

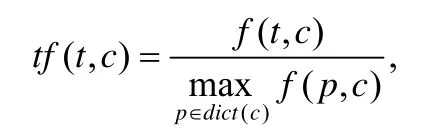
其中,dict(c)表示类属性c对应的特征字典,p表示任意特征.

我们在自然对数尺度下对特征频率进行比较分析,对频率公式tf(t,c)进行如下处理:

如果tf(t,c)值越大,则特征t在类属性c对应的实例中出现的频率越高,意味着它与类属性越相关,但不能说明它对于类属性c的鉴别性越强.为了准确度量特征的鉴别性,我们提出一个新的idf 计算公式.在定义的idf 公式的分子中用实例总数减去类属性为c的实例数,即,只考虑类属性不为c的实例中包含特征t的情况;idf 公式分母中只计数类属性不为c且包含特征t的实例数,这样可以直接反映特征t在其他各类实例中的出现频率.我们使用的类属性为c的特征t的逆文档频率idf(t,c)的计算公式为

其中,N为实例总数,Nc为类属性为c的实例数,为数据集中包含特征t同时类属性不为c的实例数.idf(t,c)值越大,说明类属性为c的特征t在其他类中出现的频率越低.基于tf-idf 的基本思想,我们定义的类属性为c的特征t的鉴别性度量值d(t,c)的计算公式为

上式说明:类属性为c的特征t在类属性为c的实例中出现的相对频率越高(tf(t,c)值越大),而在其他类实例中出现的次数越少(idf(t,c)值越大),则该特征对类属性c的鉴别性越强.即,类属性为c的特征t的d(t,c)值越大,其对类属性c的鉴别性越强.为了给出我们定义的特征的鉴别性度量公式的直观解释,下面我们通过一个计算实例来与其他研究人员常使用的tf-idf 公式进行对比.

Table 2 A calculation example of formula tf-idf表2 tf-idf 公式计算实例

表2 中ti表示第i个特征,其所在列中数字表示包含该特征的各类别实例数,ci表示第i类,Ni表示数据集中第i类实例的个数.这里,为了计算方便,我们假定每个特征在每个包含该特征的实例中的出现频数为1.

Senin 等人[19]和Schafer[28]使用的tf-idf 计算公式虽有小的不同,但本质上是一致的.这里,我们使用Schafer在文献[28]中的公式进行说明.基于文献[28]中的公式,特征t1对类属性c1的tf 值为该特征在c1类中频数取对数加 1,即,tf(t1,c1)=1+ln(5)=2.6;idf 值为数据类别总数和包含该特征的类别数的比取对数加 1,即,idf(t1,c1)=1+ln(2/2)=1;特征t1对类属性c1的鉴别性评价值为df(t1,c1)=2.6×1=2.6.

同理可得:

tf(t1,c2)=1+ln(50)=4.9;idf(t1,c2)=1+ln(2/2)=1;df(t1,c2)=4.9×1=4.9,

tf(t3,c1)=1 +ln(90)=5.5;idf(t3,c1)=1 +ln(2/2)=1;df(t3,c1)=5.5×1=5.5,

tf(t3,c2)=1 +ln(2)=1.7;idf(t3,c2)=1 +ln(2/2)=1;df(t3,c2)=1.7×1=1.7.

上面的计算公式主要存在两个问题.

(1)在tf 值的计算过程中直接对频数取对数,极大地缩小了频数间的差异.例如,c1类中特征t1和c2类中特征t1的频数比为1:10,而计算tf 值后比例变为1:1.9.

(2)idf 值不能准确反映特征的鉴别性.例如,特征t1和t3对各类别的idf 值都为1,这导致实际的鉴别性评价值仅为tf 值,不能准确反映这两个特征对不同类别的鉴别性.这是由于Schafer 在文献[28]中的idf 计算公式使用类属性取值个数和包含某特征的类的个数的比值来衡量特征对于某一类的鉴别性.然而,实际上,由于类内变异的存在,某类中的少数实例中可能具有其他类的特征,这会导致idf 度量出现偏差.

下面我们介绍基于本文定义的tf-idf 计算公式得到的特征鉴别性评价值.

首先,由于我们假定每个包含特征t的实例中特征t出现的频数都为1,因此,某类特征的最大频数不超过该类实例数.为了简便起见,在计算过程中,我们假定各类特征的最大频数为该类实例数.同时,根据表2,我们可知类别为c1的特征t1的频数为5,则其频率为5/100=0.05,因此tf 值为tf(t1,c1)=ln(1+0.05)=0.05.

由于在其他类实例(即,c2类,该类实例数为100)中包含类c1的特征t1的实例数为50,因此,根据公式(9),idf值为idf(t1,c1)=ln[(200-100+1)/51]=0.7.进而可得df(t1,c1)=0.05×0.7=0.035.

同理可得:

tf(t1,c2)=0.4;idf(t1,c2)=2.8;df(t1,c2)=0.4 ×2.8=1.12,

tf(t3,c1)=0.6;idf(t3,c1)=3.5;df(t3,c1)=0.6 ×3.5=2.1,

tf(t3,c2)=0.02;idf(t3,c2)=0.1;df(t3,c2)=0.02 ×0.1=0.002.

从上面的计算结果可以看出,基于本文的计算公式,特征t1对类c1和c2的tf 值比为1:8,与实际的频数比1:10接近,更准确地反映了特征和各类别的相关性.另一方面,特征t3的对类别c1和c2的idf 值分别为3.5 和0.1.从中可以看出,特征t3对类别c1具有更强的鉴别性.这样就有效解决了由简单地通过特征所属的类的个数进行鉴别性评价所导致的误差.因此,从计算得到的df(t,c)值更容易区分同一特征对不同类别的鉴别性.例如,基于Schafer等人给出的公式,特征t3对类别c1和c2的df(t,c)值比为3.2:1,而基于本文定义的公式比值为1050:1.综上所述,利用本文定义的鉴别性度量公式,更有利于区分各类别的鉴别性特征.

1.5 特征选择阈值设定

通过固定阈值进行特征选择忽略了不同长度滑动窗口生成的特征的分类性能,这会降低生成特征字典的的质量.为此,我们提出了一种动态阈值设定机制,该机制利用单一长度滑动窗口转换得到的特征字典对应的分类性能为其生成的特征设定阈值.首先,我们用交叉验证在单一长度滑动窗口转换得到的训练集上进行分类预测,假设获得的精度为a;然后,基于该精度和最大精度的差值为其生成特征设定选择阈值.滑动窗口对应精度越高,则其特征选择阈值越小.函数f(a)将某窗口长度精度映射为该窗口生成特征的阈值因子,定义如下:

其中,amax为单一滑动窗口获得的最大交叉验证精度.

下面我们给出不同长度窗口对应的阈值计算公式:

其中,θ为加权因子(θ＞0),al为长度为l的滑动窗口对应的交叉验证精度.

加权因子θ用于校正阈值因子存在的偏差.滑动窗口对应的交叉验证精度和最优值差距越大,则对应窗口生成特征的选择阈值越大,从而根据整体分类性能对特征进行选择可有效提升所建立的特征字典的有效性.

2 算法设计

本节对我们提出的特征字典构建算法进行详细介绍.

2.1 滑动窗口最优单词长度学习算法

各种特征包方法(BOP)的不同之处在于将实值序列转换为单词的具体过程.本文我们使用的数值序列离散化方法是SFA[22].本文提出为每个窗口长度在指定范围内动态学习性能最优的单词长度.下面首先介绍本文提出的为每个窗口长度学习最优单词长度的算法.

算法1.computeBestWindowsF(D,min,max,minF,maxF,k).

算法1 给出了本文从指定区间为每个窗口长度寻找最优傅里叶值个数(即,最优单词长度)的过程.首先,我们使用监督SFA 对训练集D进行转换得到数组AF(第2 行),其中,AF第1 维对应不同长度滑动窗口的序号,维度为max-min+1;第2 维对应训练实例的序号,维度为N;第3 维为转换后的实例,维度为对应滑动窗口从该实例上获得的子序列的个数,且实例中的每个单词长度为maxF(若滑动窗口长度小于maxF,则单词长度为窗口长度).由文献[22]可知,使用单一滑动窗口对N个实例进行监督傅里叶符号化转换的时间复杂度为O(|Wi|×wilogwi),其中,wi为第i个滑动窗口长度,Wi为该滑动窗口在数据集D上生成的子序列集合,|Wi|表示集合Wi中元素个数.由于|Wi|包含O(N×n)个子序列,wi≤n,因此,算法1 第2 步的算法复杂度为O(N×n3logn).然后,我们在转换后的数据AF的基础上从区间[minF,maxF]中学习各滑动窗口对应的性能最优的单词长度(第3 行～第12 行).

在学习各窗口最优单词长度的过程中,我们依次只使用单一滑动窗口长度对训练实例进行转换(第6 行),这一转换过程只需要截取每个单词序列(AF[i][x][y])的前j个字母即生成指定长度的单词,这一过程的时间复杂度可忽略.然后在转换得到的数据集上利用交叉验证进行预测(第7 行),并将正确预测实例数最大值对应的傅里叶值的个数作为该窗口长度对应的最优单词长度(第8 行～第11 行).整个单词长度的学习过程需执行max×maxF×k次模型训练和预测过程.本文我们使用的预测算法是一种适用于处理大规模稀疏表示数据的运行较快的逻辑回归算法[29],其算法复杂度取决于使用的梯度下降算法的收敛速度,这不在本文讨论范围之内.我们假定使用的分类模型的时间复杂度为T(n),则算法1 的时间复杂度为O(maximum(N×n3logn,max×maxF×k×T(n))).实验过程中,我们将交叉验证重数统一设为10.

2.2 鉴别性特征生成

本节我们介绍如何对训练集和测试集中的实例进行符号化转换,这一过程是算法1 中数据符号化转换的主要内容.转换过程主要分为两步.

(1)利用监督SFA 技术将时间序列或子序列转换为一组傅里叶值序列;

(2)利用离散化技术将傅里叶值转换为字母表中的字母.

傅里叶值的选择关系到时间序列及其子序列转换得来的特征的鉴别性强弱.不同位置的傅里叶值的鉴别性强弱不同.我们利用F统计量度量每个位置的傅里叶值的鉴别性,然后选择整体分类性能最优时对应的傅里叶值个数作为该长度窗口生成单词的长度,最后利用装箱技术将时间序列子序列对应的各最优傅里叶值转换为字母表中的字母,这些字母共同组成一个单词,即,特征.下面介绍本文使用的傅里叶值的挑选算法.

算法2.SelectFourierCoefficient(wi,W,bestF).

算法2 基于指定长度的子序列集合计算各个位置傅里叶值的鉴别性强弱.首先,对原始子序列进行离散傅里叶变换.由于单个长度为n的时间序列进行离散傅里叶变换的时间复杂度为O(nlogn),因此这一过程的时间复杂度为O(N×n2logn)(第2 行).矩阵A中每行对应一个子序列转换得到的傅里叶值数组,A[i]表示所有子序列的第i个位置的傅里叶值组成的数组(即,矩阵A的第i列).算法2 中依次计算第i个位置傅里叶值的鉴别性强弱统计量F值,然后将对应的傅里叶值序号和F值组成一对元组添加到集合indexBestF中(第5 行～第7 行).最后,根据F值对集合indexBestF中的元素进行降序排列(第8 行),并返回其中前bestF个元组组成的集合(第9 行～第10 行).算法2 的时间复杂度为O(N×n2logn).

获得子序列集合对应的最优傅里叶值序号数组后,我们对子序列进行符号化转换,傅里叶值符号化的过程是将reali或imagj映射到符号空间的过程.下面给出将时间序列子序列转换成特征的算法.

算法3(VLWEA).createFeature(indexBestF,S,alphabet).

算法3 给出了将时间序列子序列转换成单词的算法过程,首先,根据最优傅里叶值序号数组将转换得到的子序列傅里叶值数组S中对应位置的傅里叶值依次利用装箱技术映射为字母表中的字母(第3 行),并将获得的字母依次组合起来构成一个单词(第4 行),最后得到的单词序列即为一个特征.这一符号化转换过程需要在离散化区间中执行O(|S|×log|alphabet|)次运算[22].

2.3 特征选择和鉴别性特征字典构建

本节我们给出基于变长单词生成算法建立特征字典的过程,以及基于tf-idf 的特征选择算法.首先,给出利用可变长度的单词建立特征字典的算法过程.

算法4.createFeatureDictionary(min,max,windowBestF[],D,alphabet).

算法4 给出了基于训练集建立特征字典的算法过程.首先,遍历训练集中的每个实例(第2 行);然后,利用长度从min 到max 的滑动窗口在时间序列上进行滑动获得一系列子序列,并将这些子序列逐个转换为单词(第3行～第6 行);最后,将不重复的单词作为特征加入到特征字典中(第7 行).算法4 中特征构建过程的主要部分为训练集实例的SFA 转换过程,因此,特征库构建过程的时间复杂度也为O(N×n3logn).

基于特征包的方法转换过程中会生成规模巨大的特征字典.为提高分类模型的效率,通常需要对输入模型的特征进行选择.本文提出了一种根据不同窗口生成特征的整体分类性能来动态设定特征选择阈值的特征选算法.下面介绍本文提出的鉴别性特征字典构建算法.

算法5(TfIDfDynamicVLWEA).createTfIdfFeatureDict(dict,corrects[],θ).

算法5 介绍了本文使用的特征字典建立算法.首先计算各滑动窗口生成特征的选择阈值(第2 行～第3 行).然后,遍历字典dict中的每个特征(第4 行),计算特征的d(t,c)值(第6 行),然后将d(t,c)值大于等于其所对应的窗口阈值的特征加入到鉴别性特征字典TfIdfDict中(第9 行～第10 行).

综上所述,算法1 最优参数学习和算法4 特征库构建是本文模型的主要构成部分.因此,本文通过动态阈值构建变长特征字典模型的时间复杂度为O(maximum(N×n3logn,max×maxF×k×T(n))),其中,T(n)为参数学习过程中使用的分类模型算法复杂度.

2.4 基于特征字典的时间序列转换表示

这节我们给出基于SFA 的BOP 模型中用于训练集和测试集中实例转换的算法[24].这一过程主要分为两步:首先,在训练集上利用某长度得到的所有不重叠子序列为每个窗口长度训练用于时间序列转换的监督符号傅里叶近似转换对象,训练转换对象主要是为了计算滑动窗口子序列每个位置的F值(算法2)和用于将傅里叶值数组进行离散化的分箱区间(文献[23]中有详细介绍);然后,用训练得到的转换对象对时间序列进行转换[24].下面我们给出时间序列的转换算法.

算法6.SupervisedSFATransform(TfIdfDict,T,min,max,transferObjects[]).

算法6 给出了将一条时间序列转换为符号序列频数数组的算法.该算法用指定长度滑动窗口从给定时间序列的初始位置进行滑动依次获得一系列可重叠的子序列(第2 行～第3 行),然后通过对应长度的监督符号傅里叶近似转换对象将每个子时间序列依次转换成一个单词,即,时间序列包含的特征(第4 行).若转换得到的特征在给定的鉴别性特征字典中,则将该特征加入到转换后的实例中,作为转换后实例的一个特征(第5 行～第6 行).此时,若转换后的实例中没有该特征,则为转换实例加入该特征,并将该特征的取值设为1;若转换后的实例中已有该特征,则该特征对应的值加1.最后返回获得的特征频数序列,即为转换得到的时间序列.

逻辑回归(logistic regression)是统计学中的经典分类方法.它是一个对数线性模型.本文我们使用基于L2正则化的逻辑回归模型对转换后的实例进行分类[29].此外,本文还利用逻辑回归学习到的权重对特征字典进行分析.

3 实验分析

本节对我们所提模型的相关实验内容进行详细介绍.主要包括4 个方面:模型参数分析、模型设计的方法分析、分类精度比较和模型的可解释性分析.本文在UEA & UCR 时间序列知识库提供的65 个长度小于750的时间序列数据集上对模型进行分析[30].表3 给出了各数据集的信息,其中,Train/Test 表示训练集和测试集的实例数,n为时间序列长度,|C|为类属性取值个数.我们的实验环境CPU 是3.40GHz,内存为16G.

Tabel 3 Introduction to 65 time series datasets表3 65 个时间序列数据集介绍

3.1 模型参数实验分析

本节我们对模型TfIDfDynamicVLWEA 的几个重要参数进行实验分析.

(1)训练集规模和时间序列长度对模型运行时间的影响分析;

(2)模型精度和压缩比(即,TfIdf 特征库中特征数和初始特征库中特征数的比值)对阈值加权因子θ的敏感性;

(3)模型精度对最大滑动窗口长度和最大单词长度的敏感性.

首先,分析模型的运行时间分别与训练集规模、时间序列长度的关系.我们使用一个生成的二分类数据集进行实验.训练集和测试集中各包含100 个长度为200 的时间序列,且每个数据集中两类实例个数相同.在实例数递增分析实验中,我们设置初始训练集和测试集各由原数据集中10%的实例构成,然后训练集和测试集中实例个数以原训练集实例个数的10%递增,并始终保持数据集中类属性分布和时间序列长度不变.我们分别统计模型在上述10 组数据上的运行时间.在时间序列长度递增分析实验中,我们将时间序列长度从原长度的10%开始按10%递增,同时保持训练集和测试集规模不变,这样进行10 组实验并统计模型运行时间.图2 给出了模型TfIDfDynamicVLWEA 的运行时间的实验结果.

从图2 可以看出,模型TfIDfDynamicVLWEA 的运行时间与训练集实例个数呈线性关系,而与时间序列长度呈多项式关系.这与第2 节分析获得的模型算法复杂度相符.

下面我们在10 个数据集上对模型各参数的敏感性进行分析.图3 和图4 中加粗曲线表示10 个数据集上模型TfIDfDynamicVLWEA 的平均精度变化曲线,我们标出了每个点对应的平均精度.

首先,我们分析加权因子对模型TfIDfDynamicVLWEA 的精度和特征库压缩比的影响.从图3(b)中可以看出,随着θ的增大,压缩比显著减小,当θ大于5 后,减速变缓.同时,从图3(a)中可以看出,随着θ的增大,数据集精度呈现出不同的变化趋势.例如,数据集Beef 和Ham 上的模型精度随θ增大,先增大后减小;数据集BeetleFly、ShapeletSim 等的精度随θ增大,变化不大;数据集Herring 的精度随θ增大,呈现先减小后增大的趋势.由于当θ为3时,模型的平均精度最大,压缩比较优,因此综合考虑,我们选择将模型的参数θ设为3.

Fig.2 The running time of model TfIDfDynamicVLWEA图2 模型TfIDfDynamicVLWEA 运行时间分析

Fig.3 Analysis of the influence of the parameter θ on model TfIDfDynamicVLWEA图3 模型TfIDfDynamicVLWEA 参数θ的影响分析

图4 给出了10 个数据集上模型TfIDfDynamicVLWEA 精度及平均精度随最大滑动窗口长度和最大单词长度的变化趋势.

从图4(a)和图4(b)可以看出,不同数据集对不同参数的敏感性不同.从图4(a)中可以看出,Lightning7 数据集上的精度随最大滑动窗口长度的递增总体呈增长趋势,数据集 ShapeletSim、BeetleFly、Symbols、ToeSegmentation1 和Ham 对最大窗口长度不敏感,数据集Beef 和Herring 对最大滑动窗口长度较为敏感,随窗口长度呈递增趋势,精度变化明显.上述实验结果表明,很难设定最优滑动窗口长度.由于最大滑动窗口长度取250 时,图4(a)中平均精度值最大,同时也为了保证对比实验的公平性,我们将模型TfIDfDynamicVLWEA 的最大窗口长度设为250.

从图4(b)可以看出,数据集Beef 和Herring 对最大单词长度较为敏感,数据集ShapeletSim、BeetleFly、Car、Symbols 和ToeSegmentation1 对最大窗口长度不敏感,数据集Ham、Lightning7 和ToeSegmentation2 随最大单词长度发生变化,精度有波动.在区间[8,18]中10 个数据集上的平均精度在15 时最大,因此,我们将模型中TfIDf DynamicVLWEA 的最大单词长度设为15.

此外,由于目前基于SFA 对时间序列进行符号转换的研究[19,23,24]表明字母表大小设置为4 时,BOP 模型具有更强的鲁棒性.因此,本文将字母表大小固定为4.

Fig.4 Sensitivity analysis of model TfIDfDynamicVLWEA accuracy to parameters max and maxF图4 模型TfIDfDynamicVLWEA 精度对参数max 和maxF 的敏感性分析

3.2 设计方法分析

我们在表3 中的65 个数据集上对本文所提模型中设计的新方法进行分析.主要包括如下3 个方面.

(1)可变单词长度和固定单词长度比较;

(2)Bigrams 特征对可变长度特征字典性能的影响;

(3)基于tf-idf 统计量的特征选择算法和基于卡方统计量特征选择算法的比较.

我们使用符号VLWEA 表示采用可变长度单词生成算法的特征字典建立模型,FLWEA 表示采用固定长度单词生成算法的特征字典建立模型.VLWEA_U、FLWEA_U 分别表示对应模型在特征字典建立过程中只将单个单词作为特征,且不对特征进行选择.FLWEA_B、VLWEA_B 分别表示模型在特征字典建立过程中使用Bigrams 语法模型进行特征生成,即,将连续的两个单词组成一个新的单词作为特征.符号Chiδ和TfIdfδ分别表示模型中使用单一阈值的特征选择算法,其中,δ表示使用的阈值.例如,Chi3VLWEA_U 表示模型VLWEA_U 中使用阈值为3 的卡方统计量进行特征选择,即,保留卡方统计值大于等于3 的特征.TfIDfDynamicVLWEA 表示本文提出的使用动态阈值设定的VLWEA 模型,其中加权因子θ统一取为3.我们使用的对比模型包括:不利用Bigrams 语法进行特征生成,只利用可变长度单词或固定长度单词组成的特征字典建立模型VLWEA_U 和FLWEA_U,结合不同特征选择算法和不同阈值的模型Chi3FLWEA_U、Chi3VLWEA_U、TfIdf0.3VLWEA_U、TfIdf0.3VLWEA_B 和TfIDfDynamicVLWEA_U.实验中,上述所有VLWEA 和FLWEA 模型的最小和最大滑动窗口长度都分别设为4 和250,字母表的大小统一设定为4,其他处理方式与定长单词生成模型WEASEL 相同.同时,使用相同参数设置的分类模型对转换后的测试集进行分类预测.

接下来,我们利用Demsar 提出的模型分类性能显著性和平均排名比较方法在65 个数据集上对本文新提出的方法进行分析[31].表4 中给出了多种条件下建立的特征字典对应的逻辑回归模型在65 个数据集上的分类精度、平均精度和模型在65 个数据集上精度最高的数据集个数.表4 中给出的模型实验结果都是通过在每个数据集上进行5 次实验取均值获得的.在对特征选择算法的性能对比过程中,为了对比实验的公平性,我们通过选取适当的阈值,使得不同特征选择算法在65 个数据集上的平均压缩比相近,即,65 个数据集上选择后的特征字典大小和原特征字典大小的比的平均值相近.模型TfIdf0.3VLWEA_U、TfIdf0.3VLWEA_B、Chi3VLWEA_U和Chi3FLWEA_U 的平均压缩比分别为27.3%、24.6%、32.6%和36.3%.

从图5 中我们可以看出:使用阈值为3 的卡方统计量进行特征选择的定长单词生成模型Chi3FLWEA_U 的性能排名最低,这说明可变长度单词生成算法有助于提升模型分类性能.使用本文定义的鉴别性特征评价统计量进行特征选择的变长单词生成模型TfIdf0.3VLWEA_U 在65 个数据集上特征字典的平均压缩比优于基于卡方统计量的特征选择算法模型(Chi3VLWEA_U 和Chi3FLWEA_U)压缩比的条件下,分类性能排名更优.这说明,本文提出的基于tf-idf 的特征选择算法与基于卡方统计量的特征选择算法相比,能够更有效地进行特征选择.与此同时,从图5 中我们还可以看出:在相同阈值条件下,结合Bigrams 语法的特征生成模型TfIdf0.3VLWEA_B 的排名低于模型TfIdf0.3VLWEA_U,这说明,Bigrams 语法模型不能有效地提升变长特征生成算法的分类性能.因此,综合考虑生成特征字典规模和分类模型的运行效率,在接下来的对比实验中,我们的模型中不再采用Bigrams 语法进行特征生成.此外,基于动态阈值的特征选择模型TfIDfDynamicVLWEA_U 在65 个数据集上的性能平均排名第1,这显示了本文提出的动态阈值设定算法的有效性.从表4 中我们还可以看出,TfIDfDynamic VLWEA_U 在65 个数据集上的平均精度最高和精度最高的数据集个数最多.因此,在接下来的实验分析中,我们使用TfIDfDynamicVLWEA_U 模型与其他各类模型进行对比,并将其简记为VLWEA.

Fig.5 The classification performance significance analysis and the average rank of the dictionaries built under 6 conditions on 65 datasets图5 6 种条件下构建的字典在65 个数据集上的分类性能显著性分析和模型平均排名

3.3 分类精度比较

本节我们将本文所提鉴别性特征字典建立模型VLWEA 分别与基于特征包的模型、1NN 模型、基于shapelet 的模型和集成分类模型的分类精度进行对比分析.两个常用的基准1NN 分类模型为:基于欧式距离的1NN(ED1NN)和基于动态时间规整的1NN(DTW1NN);两个基于Shapelet 的非集成分类模型包括:快速Shapelet分类(fast Shapelet,简称FS)[32]算法和Grabocka 等人提出的基于启发式Shapelet 搜索算法的分类(learning Shapelets,简称LS)模型[33];6 种特征包模型为:SAXVSM、BOSS、TSBF、使用Bigrams 语法进行特征生成的模型WEASEL_B、使用Unigram 语法进行特征生成的WEASEL 模型WEASEL_U 以及Kate 等人提出的基于DTW 距离的特征生成算法(DTW features,简称DTW_F)[34];3 种集成分类模型包括:Deng 等人提出的基于11 种近邻分类模型的集成分类算法(elastic ensemble,简称EE)[35]、基于Bostrom 等人提出的Shapelet 转换表示方法建立的集成分类模型(ST)[16]和COTE.模型WEASEL_B 和WEASEL_U 的参数设置采用Schafer 等人提供的代码中的默认设置,模型预测精度我们取5 次实验的平均值(见表4,其中,C2FB 代表WEASEL_B,C2FU 代表WEASEL_U),其他模型采用Bagnall 等人[5]提供的实验结果.下面我们将本文模型和各类模型在65 个数据集上分别进行对比,并给出了VLWEA 和对比模型相比在65 个数据集中的精度高、平、低的数据集个数,例如,“30/20/15”表示和对比模型相比,VLWEA 有30 个更准确,20 个相同,15 个更差.

首先,我们对VLWEA 和6 个BOP 模型的比较结果进行分析.从图6 和具体的“高/平/低”对比结果统计可以看出,VLWEA 模型与模型 WEASEL_B(35/9/21)、WEASEL_U(41/6/18)、TSBF(48/5/12)、BOSS(35/2/28)、SAXVSM(55/2/8)及DTW_F(51/2/12)相比,分类精度高的数据集个数都是最多的.VLWEA 在不使用Bigrams 语法进行特征生成的条件下,比WEASEL_B 在更多的数据集上取得更好的分类效果.这再次说明本文可变长度单词生成算法在特征生成上的有效性.

从图7 中和具体的“高/平/低”对比结果统计可以看出,VLWEA 与模型ED1NN(60/1/4)和DTW1NN (53/3/9)相比显著更好,分类效果具有绝对优势.

图8 和对比结果统计说明,VLWEA 和2 个不使用集成分类算法的基于Shapelet 的分类模型LS(49/6/10)、FS(60/3/2)对比同样具有显著优势.

图9 和具体的精度“高/平/低”对比结果统计说明,VLWEA 和3 个集成分类模型COTE(27/7/31)、EE(45/3/17)、ST(40/6/19)相比,比EE 和ST 更好,但比COTE 略差.

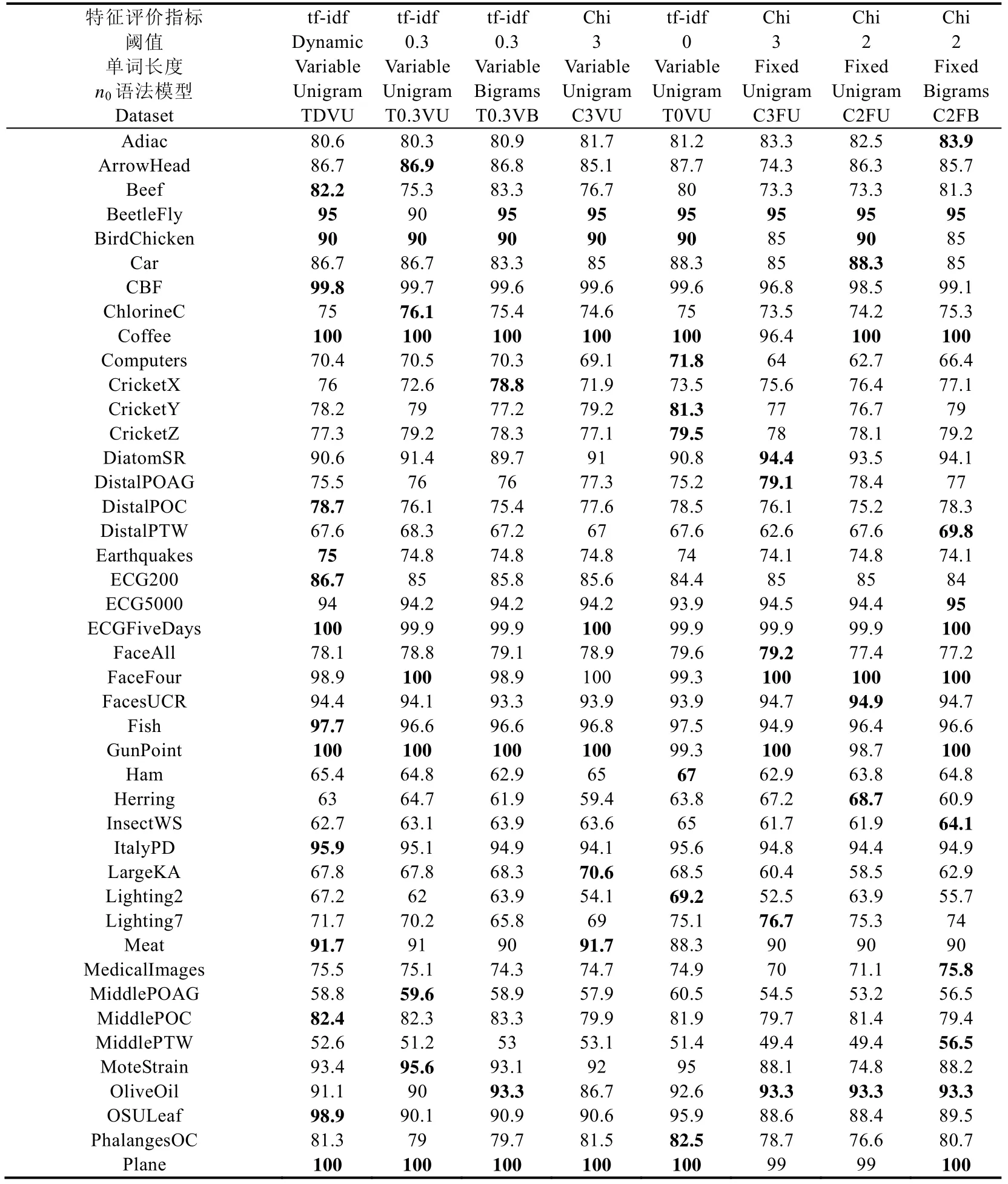
Tabel 4 Accuracies of the feature dictionaries built under eight different conditions (%)表4 8 种不同条件下建立的特征字典对应的模型分类精度(%)

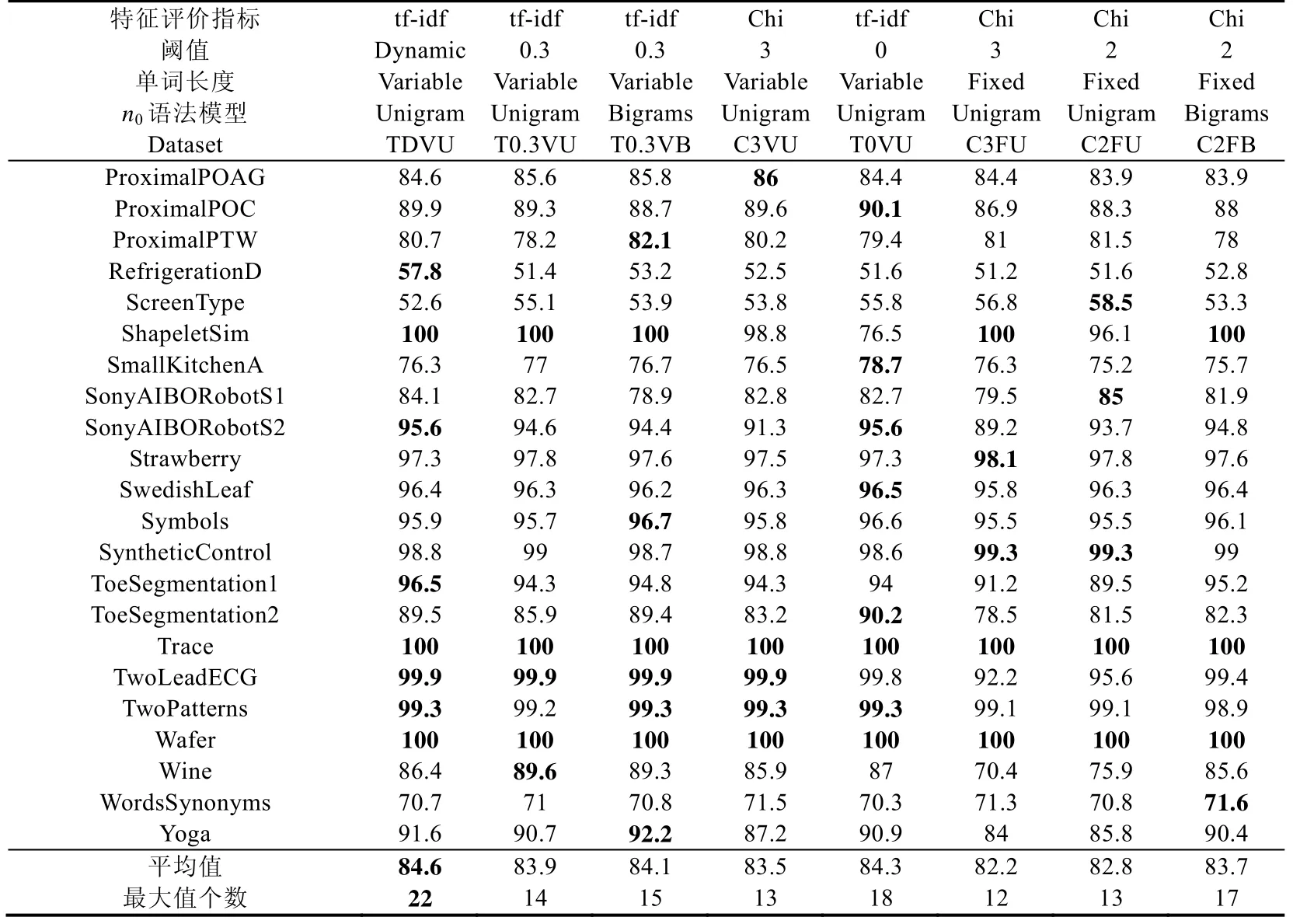
Tabel 4 Accuracies of the feature dictionaries built under eight different conditions (%)(Continued)表4 8 种不同条件下建立的特征字典对应的模型分类精度(%)(续)

上面表4 中我们将各特征字典构建模型符号表示中的TfIdf 简记为T,Chi 简记为C,Dynamic 简记为D,VLWEA_X 和FLWEA_X 分别简记为VX 和FX,X 表示使用的n0元特征生成模型,U 表示Unigram,B 表示Bigrams.例如,模型TfIDfDynamicVLWEA_U 记作TDVU.表4 中每行加粗数值表示对应行的最优值.

Fig.6 Comparison of accuracy between VLWEA and 6 BOP models on 65 datasets图6 VLWEA 和6 个BOP 模型在65 个数据集上的分类精度比较

Fig.7 Comparison of accuracy between VLWEA and 2 1NN models on 65 datasets图7 VLWEA 和两个1NN 模型在65 个数据集上的分类精度比较

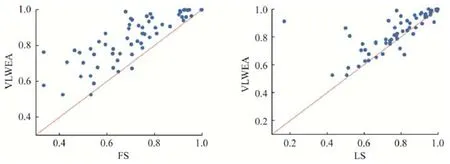
Fig.8 Comparison of accuracy between VLWEA and 2 shapelet models on 65 datasets图8 VLWEA 和两个Shapelet 分类模型在65 个数据集上的分类精度比较

Fig.9 Comparison of accuracy between VLWEA and 3 ensemble models on 65 datasets图9 VLWEA 和3 个集成分类模型在65 个数据集上的分类精度比较

最后,我们对本文提出的模型VLWEA 分别与其同类型和异类型模型的性能显著性和平均排名进行对比分析.从后文所示图10 可以看出,VLWEA 与其他6 个BOP 模型在65 个数据集上的性能相比没有显著差异,但是VLWEA 的分类精度排名最高.与非BOP 模型相比,VLWEA 的排名只比COTE 差,比ST、EE、LS、FS、ED1NN和DTW1NN 的排名都更好.与当前最先进的模型的对比结果说明了本文所提出的特征字典建立方法的有效性.

3.4 实例分析

本节对VLWEA 模型的可解释性进行分析.我们选择多分类数据集CBF 对模型学习到的最优单词长度和生成特征的鉴别性进行分析.该数据集的训练集实例共有3 类.我们用每类实例各特征的频数平均值组成一个均值序列代表该类实例.图11 给出了CBF 各窗口长度的最优单词长度的箱型图和9 个由原始序列生成的鉴别性子序列图示.

从图11(a)可以看出:在忽略极少数异常值的情况下(如图11(a)中的长度15),25%的最优单词长度落在[3,4]之间,50%的最优单词长度落在区间[4,7]中,25%的最优单词长度位于[7,11]之间,因此,固定长度单词生成算法在单词生成过程中会不可避免地损失鉴别性信息或携带大量冗余信息.从图11(b)可以看出,本文提出的可变长度单词生成算法可以有效地学习最优单词长度.例如,图中不同长度:24、27、50、16 和120 对应的特征分别有针对性地将原序列尾部的冗余信息“**…*”去除(符号“*”代表字母表中的任意字母),只保留具有鉴别性的部分.此外,对于图11(b)所示长度为120 的4 个原始序列,若单词长度为2,则只生成一个特征“cc”;单词长度为3 时,生成特征“ccb”和“ccd”;单词长度大于4 时,可以生成4 个特征,但会包含一定冗余信息.而本文算法可以有效学习单词的最优长度,且不包含冗余信息.这也再次验证了图11 给出的示例.

Fig.10 The classification performance analysis and the average ranks of VLWEA and 13 models on 65 datasets图10 VLWEA 和13 个分类模型在65 个数据集上的分类显著性分析及平均排名

Fig.11 Optimal word lengths and 9 generation features obtained by VLWEA图11 VLWEA 学习得到的最优单词长度和9 个生成特征

由于建立的特征字典规模巨大,我们根据学习到的权重选择top-10 个特征对数据集进行表示.图12 中给出了3 类实例均值序列的直方图.从图12 中我们可以看出,这些特征具有明显的鉴别性,例如,特征“74ccadd”只有类属性为c0的实例具有,特征“29ccbbb”和“29acbbb”特征对于类属性为c1的实例具有较强的鉴别性.具有特征“54ccbcd”和“74ccbdd”的实例类属性为c1的可能性很小.

Fig.12 Top-10 discriminant features generated by VLWEA on dataset CBF图12 数据集CBF 上VLWEA 生成的top-10 鉴别性特征

4 结 论

在进行时间序列数据挖掘之前,对时间序列数据重新表示是一个重要的研究课题,其目的是,一方面通过减少算法实际处理数据的量来提高算法的运行速度,另一方面,充分表达原始时间序列数据的本质内容以提高分类精度.针对目前基于SFA 的时间序列进行离散化表示方法存在的问题,本文提出了一种可变长度单词抽取算法,该算法可以有效学习不同滑动窗口对应的最优单词长度.与此同时,针对特征字典规模巨大的问题,本文定义了一种新的鉴别性特征选择统计量,并设计了一种动态阈值设定机制来对生成的特征进行选择,该方法在有效缩小特征字典规模的同时,可以获得较高的分类精度.