基于粒子群优化灰色神经网络的机床主轴热误差建模
2020-01-01王建军
冯 伟 ,王建军
(1.中国一拖集团有限公司,河南 洛阳471004;2.西安交通大学机械工程学院,陕西 西安710049)
热误差是机床的主要误差源,研究表明热误差占机床总误差的40%~70%[1],尤其在精密机床中所占比例更大。主轴是机床的关键部件,由温度导致的主轴热变形会严重影响机床的加工精度[2]。对热误差进行准确的预测并实施补偿,对于提高机床的加工精度具有重要意义。
国内外在热误差建模方面做了大量研究[3],已经发展了诸如多元线性回归[4]、人工神经网络[5]、时间序列[6]、灰色理论[7]、动态神经网络[8]等多种热误差模型。人工神经网络具有较强的非线性预测能力,因此能够更好的预测机床热误差。BP神经网络是应用最广的神经网络,但存在收敛速度慢容易陷入局部最优解的缺点。王春暖等[8]建立了基于改进粒子群优化BP神经网络的机床热误差模型,能够避免预测结果陷入局部最优解,且预测的精度优于普通BP神经网络和支持向量机。但输入神经网络的时间序列中存在较大的随机性和不确定性,遗传算法采用概率的变迁规则指导搜素方向,能够很好处理BP神经网络权重初始化的随机性问题,Huang等[9]采用遗传算法优化BP神经网络进行热误差建模,预测的精度得到很大提高。然而,遗传算法存在编程实现复杂的缺点,为此本文提出基于粒子群优化灰色神经网络的建模方法,采用灰色神经网络(GNN)修正网络的权值阈值,然后利用粒子群算法(PSO)获取最优权值阈值得到主轴热误差模型,从而进一步提高模型预测的精度。
1 热误差建模
1.1 温度测点优化
通过对温度测点进行优化,减少温度测点个数,提高模型运算效率和精度。在这里计算各温度测点与热误差之间的相关系数,在同组中得出对热误差影响最大的点。
设温度测点序列 T={T1,T2,…Tm},Ti={Ti1,Ti2,Ti3,…Tin},其中m为总共温度测点数,n为时序上的总共测量次数,热误差测量序列为E={E1,E2,…En},通过相关系数公式可以计算得出各温度测点和热误差之间的相关系数。
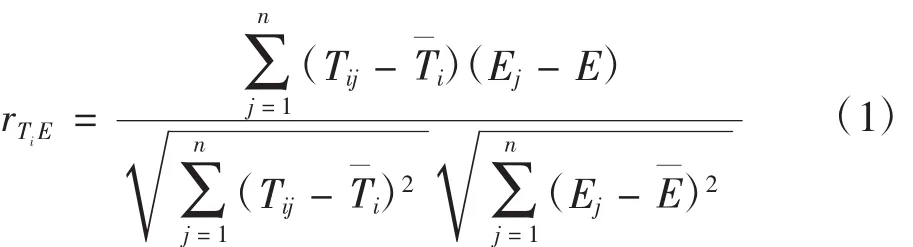
1.2 BP神经网络
BP神经网络是在工业上应用最广的神经网络,具有反向误差传播结构,可以对网络的权值阈值进行修正。BP神经网络可以看作非线性拟合函数,在BP网络中首先要对网络进行训练,使其具有联想和预测能力,然后输入要预测的数据进行预测。
在该网络中具有输入层、隐含层和输出层三层结构。在这里设置网络的结构为3-7-2,其中隐藏层节点数7是根据Kolmogorov定理进行选择,最大迭代次数设置为1000,学习目标设置为0.1,学习率设置为较大值时会加快网络收敛,但在最佳值时会产生震荡使之无法收敛,应设置为较小值,这里设置为0.25,动量因子设置为0.9,输入层到隐藏层的传递函数设置为‘tansig',隐藏层到输出层设置为‘purelin'。
1.3 灰色神经网络
灰色模型可以对缺少规律的问题进行白化处理,挖掘数据深层次的有用信息去揭示未知信息,在灰色神经网络中采用了BP神经网络的误差反向传播的结构,可以有效地修正网络的权值阈值[10]。
在灰色神经网络中,需要对原始数列进行一次累加处理,得到呈指数增长的数据序列。从而可以以一个微分方程的形式进行数据的拟合和预测。n个输入参数的微分方程表达式如下:
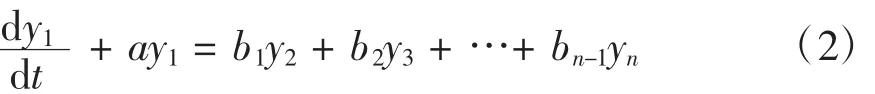
其中 a,b1,…,bn-1为网络的 n 个输入参数;y2,…,yn为系统输入参数;y1为系统的输出参数。得到的微分方程的时间响应式为:
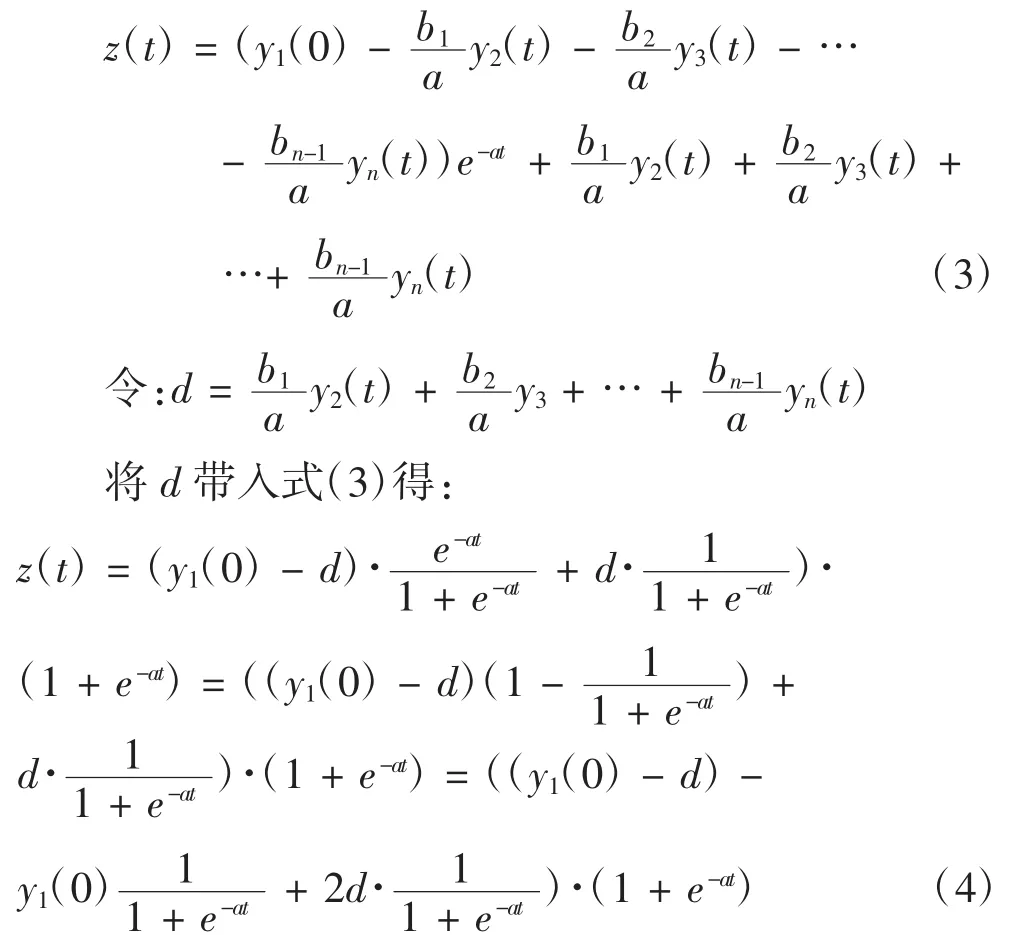
变换后的式(4)映射到拓展的BP神经网络可以得到n个输入一个输出的灰色神经网络。网络拓扑结构如图1所示。
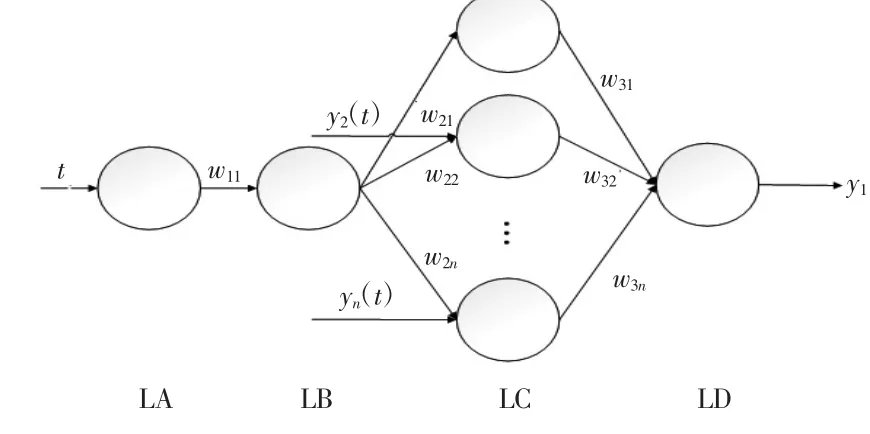
图1 灰色神经网络拓扑结构
1.4 PSO优化灰色神经网络
PSO算法最早是由Kennedy和Eberhart根据鸟类捕食行为提出,在PSO算法中每个粒子都作为鸟群中的鸟的角色,每个粒子的位置信息都作为问题的可能解。在算法中每一个粒子都通过适应度函数得出的适应度值来判断自身位置的好坏,在PSO算法中每个粒子还必须具有记忆功能,用以记录自己所经过的位置,通过社会共享行为来进行自身速度和方向的调整来获得最优位置[11]。
在PSO算法中寻优公式如下:
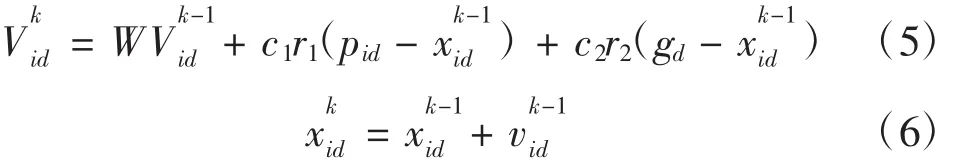
在灰色神经网络中因为随机赋值,导致网络容易陷入局部最优解。在PSO优化的灰色神经网络中用PSO算法对初始参数进行优化,有效的避免灰色神经网络在迭代过程中陷入局部最优,在PSO优化的网络中选择灰色神经网络的预测值和实际测量值的绝对误差作为适应度函数,流程图如图2所示。

图2 PSO优化灰色神经网络流程图
在PSO优化的灰色神经网络中设置学习因子c1、c2为 2.05,粒子长度设置为 4,种群规模(粒子数)设置为30,PSO算法优化部分设置为100代,最大限制速度设置为5,权值最大值和最小值分别设置为0.9、0.4,在优化的灰色神经网络中迭代次数设置为100代。
2 热特性试验
2.1 实验装置及实验方案
该实验以XK63100机床为研究对象,采用NI公司数据采集系统实时获取主轴系统温度及热变形数据,如图3所示。测点温度由磁K型热电偶测量,主轴热漂移量由电涡流传感器测量。用7个热电偶获取机床主轴的温度场,主轴主要热源为轴承,由于后轴承封在主轴齿轮箱中,因此主要测前轴承、主轴部分温度,环境温度作为参考,温度测点布置如表1所示。采用五个电涡流传感器分别测量主轴热伸长及径向倾斜,热变形测量示意图如图4所示,温度和热变形测量现场如图5所示。

图3 实验测量系统

表1 温度传感器布置
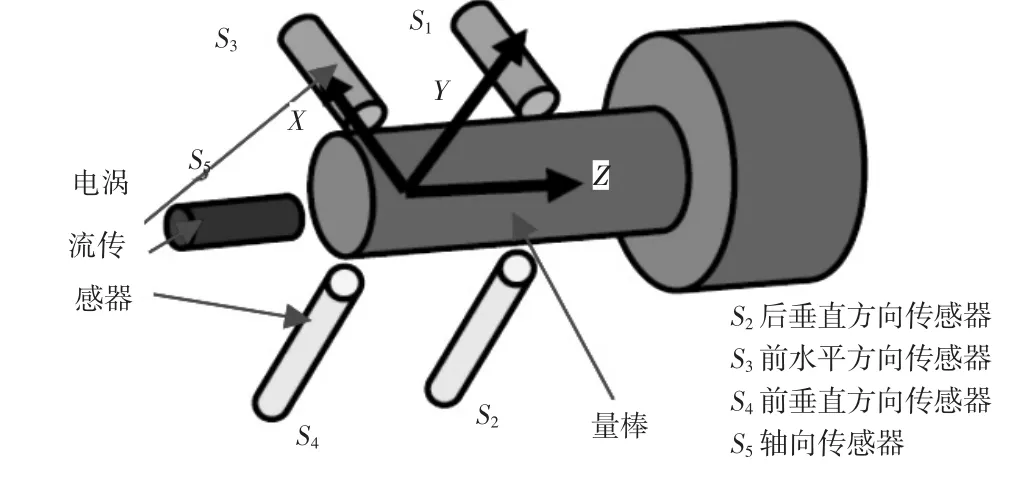
图4 热变形测量示意图

图5 主轴温度场和热变形测量
主轴转速按照热机时的转速(800 r/min)从冷态开始加热210 min,模拟实际加工过程中主轴转速变化,设定主轴转速在0~1 500 r/min范围内按阶梯变化并设定每15 min变换1次转速,共连续运行135 min,主轴转速图如图6所示。
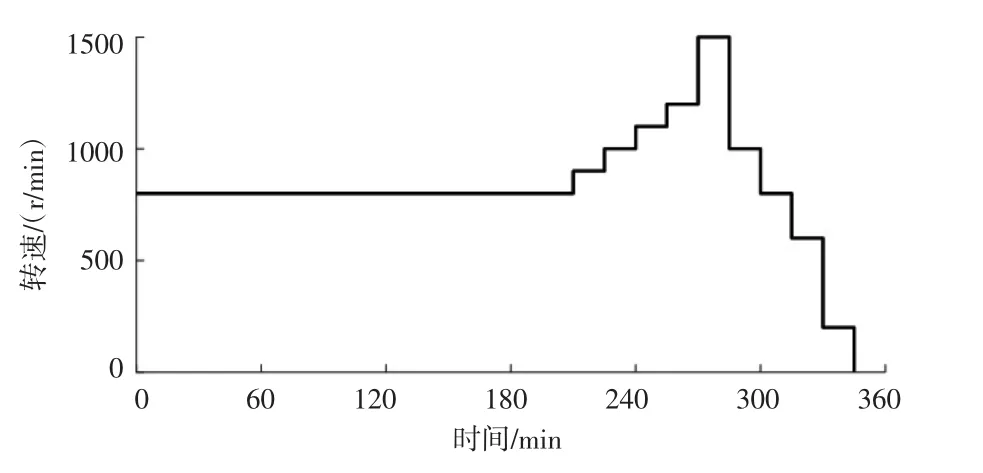
图6 主轴转速图
通过五点法采集的热变形数据可计算得出主轴俯仰角 θy和偏摆角 θx, 计算公式如下:
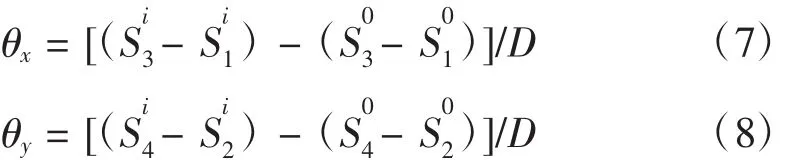
2.2 实验结果
主轴热特性实验获得的温度场如图7(a)所示。随着主轴转速增加,各测点温度总体不断增大,约250 min主轴前端和前轴承温度达到最高,其中前轴承发热最为严重,最高温度达到49.8℃,主轴前端和后端最高温度分别为37℃和31.1℃。主轴后端温度在250 min时还在缓慢上升,在310 min时达到最高31.1℃。由于结构限制,无法得到主轴内部的温度,测点温度只是一种近似,但测量结果也能反映温度随时间变化情况。另外,车间室温随外部环境温度变化也略有变化,但变化不大,在2~3℃左右。

图7 主轴热性能
实验获得的主轴热变形如图7(b)所示。随着温度的升高,主轴热变形逐渐增大。约经过250 min主轴轴向伸长最大达到210.9 μm,主轴前端垂直方向最大偏移89.7 μm,后端垂直方向最大偏移量82.2 μm,主轴在垂直方向表现出“抬头”现象。主轴前端水平方向最大偏移58.0 μm,后端水平方向最大偏移量55.6 μm,主轴在水平方向发生倾斜。通过转速图、主轴温度场图和主轴热变形图的对比,可知主轴转速、热变形与温度呈近似比例变化,然而热变形相对于温度场存在滞后现象,这主要是由于主轴结构热惯性的存在。试验获得的主轴热倾角如图8所示。
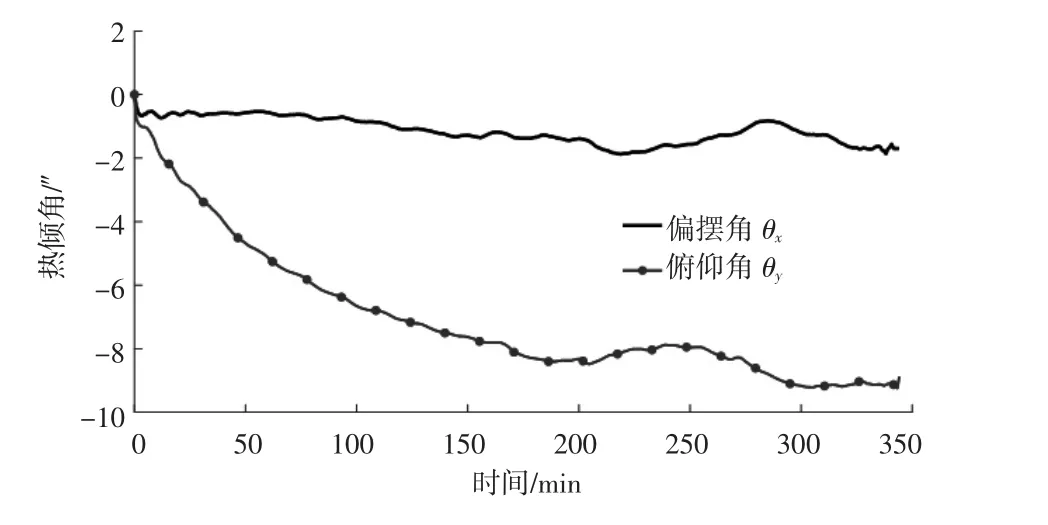
图8 主轴热倾角
3 模型性能比较
3.1 温度测点选择
该数据在采集时已经进行分组,从图7(a)中可以看出温度数据分为三组,只需相关系数计算即可,在这里选择轴向热误差进行相关系数的计算,经过式(1)计算得出温度测点相关系数值如表2所示。

表2 温度变量相关系数
对比各组相关系数值选出三个温度测点T1、T4、T5,用这三个温度测点进行网络训练。
3.2 模型预测
选择优化后的三个温度测点作为各个网络的输入,轴向热变形和俯仰角θy作为网络的输出,将选择的的温度数据、热变形数据和热倾角数据进行归一化处理,以加快网络收敛。并在每个网络中用所选数据的前260 min对应的数据进行训练,用剩下的85 min数据预测。轴向热误差预测如图9(a)所示,俯仰角 θy预测如图 9(b)所示。
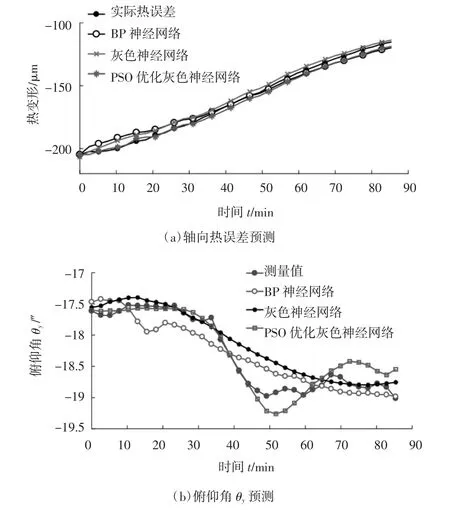
图9 模型预测
PSO优化灰色神经网络值得到的最优初始参数分别为 a1=0.530 2,b1=0.384 6,b2=0.453 2,b3=0.637 0,得到的个体适应度曲线如图10所示。

图10 最优个体适应度
3.3 模型性能比较
通过对预测数据和实际数据做差可以得到残差图,轴向热变形残差如图11(a)所示,俯仰角θy残差如图11(b)所示。通过残差图可以看出PSO优化灰色神经网络预测残差波动范围相比于其他的两个网络较小,计算得出PSO优化网络得出的轴向热伸长和俯仰角θy平均残差分别为2.293 μm和0.134 μm;灰色神经网络的出的平均残差分别为3.075 μm和0.181 μm;BP神经网络得出的平均残差分别为3.546 μm 和 0.215 μm。
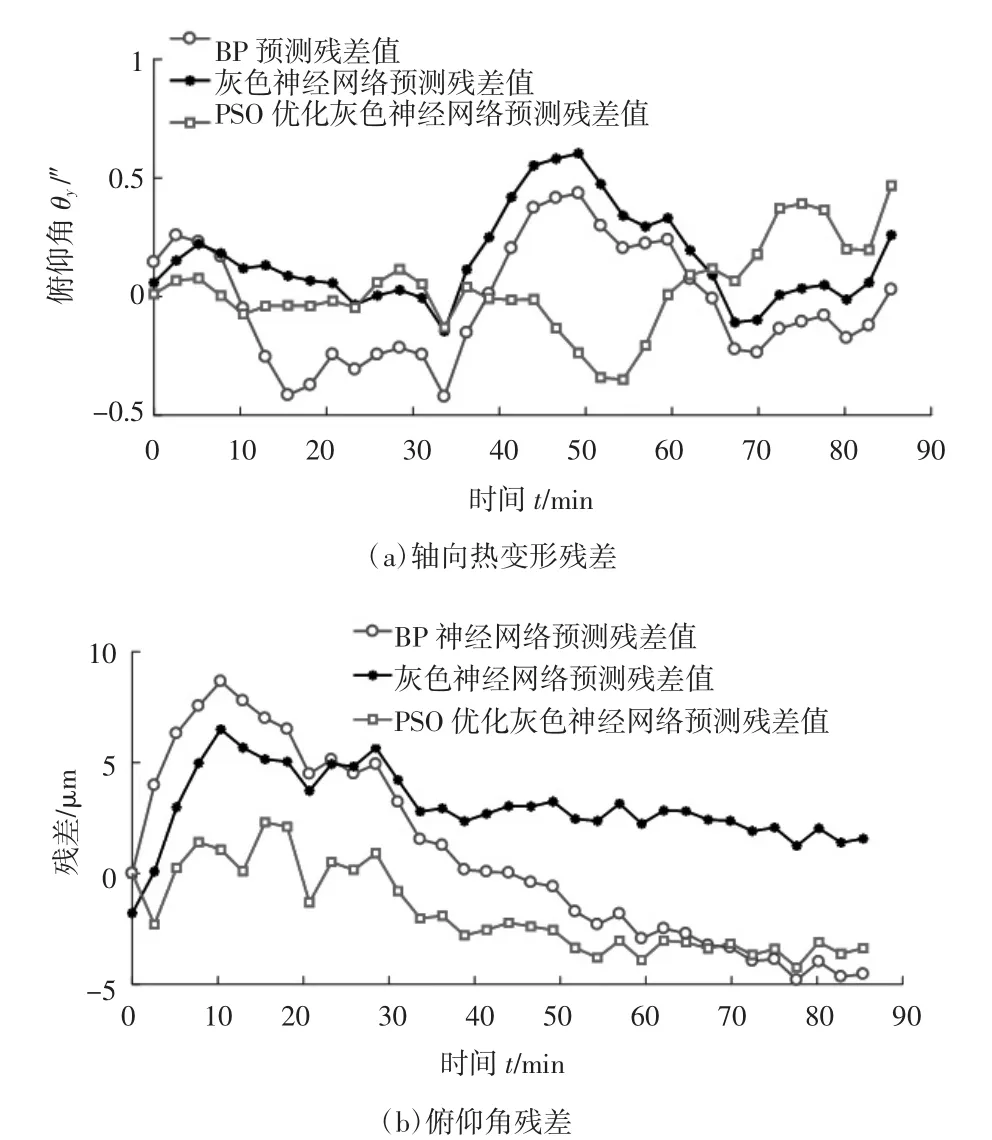
图11 网络预测残差
计算预测值与实际值的平均相对误差得出PSO优化的灰色神经网络预测轴向热误差和热倾角的相对误差分别为1.55%和0.72%;灰色神经网络预测的平均相对误差分别为1.91%和0.99%;BP神经网络预测平均相对误差分别为2.21%和1.20%。从这些平均残差和相对误差中也可以看出PSO优化后的网络预测精度得到了改善,有效的避免了局部最优解的出现。
4 结束语
本文建立了PSO优化的灰色神经网络的轴向伸长和俯仰角模型,并将该模型的预测性能与灰色神经网络BP网络进行对比,得出以下结论:
(1)该网络预测得出的轴向热伸长和俯仰角θy平均残差分别为2.293 μm和0.134 μm。
(2)计算该网络预测得出数据的平均相对误差分别为1.55%和0.72%,均小于灰色神经网络和BP网络的预测平均相对误差。
(3)PSO算法能够实现对灰色神经网络的初始参数进优化,并能有效提高网络模型的收敛性和预测精度。为主轴热误差补偿模型提供了一种新的方法。
