基于schijf方法的船闸通航船舶下沉量预报

李俊敏， 李铃杰 ， 孙艳兵

(武汉理工大学 a.交通学院； b.高性能船舶技术教育部重点实验室， 湖北 武汉430063)

0 引 言

随着西部大开发和长江经济带经济发展的需要，长江水运蓬勃发展，东西部地区的水运物资对流日益增加。2010年货运量为7 880万t；2011年达10 032万t，首次突破1亿t(提前19年达到设计通过能力)，比上一年同比增长27.3%；2017年更是达到1.38亿t(超过设计通过能力的38%)；三峡船闸通过量年均增长11%[1]。三峡通航管理局提供的数据显示：2014年，三峡船闸每天过闸船舶需求量为130～170艘，运输繁忙季节超过180艘，正常情况下每天能安排140艘左右的船舶过闸，船舶平均待闸时间约为33 h[2]。此外，三峡船闸的设计日过闸次数为 22.1次，闸次间隔时间为 59.7 min，昼夜平均工作时间为 22 h。从实际运行情况看，2005年-2011年，船闸日均过闸次数分别为 12.3 次、11.5 次、11.8 次、12.7 次、11.9 次、13.3 次、14.3 次，远低于设计日过闸的22.1次[3]。据不完全统计，2017年正常时期，最大船舶待闸量达1 200艘，检修期间达1 500艘。由此可见，三峡船闸目前压船现象十分严重。

在确保船舶安全通过三峡船闸的前提下，研究进闸船舶的极限装载吃水或过闸极限航速是提升三峡船闸船舶通过量和货运量的有效途径。其中,进闸船舶下沉量预报是研究进闸船舶极限装载吃水或过闸极限航速的基础，因此开展船闸通航船舶下沉量预报研究具有十分重要的科研与工程应用价值。

文献检索表明，船舶进闸下沉量的国内外文献较少。其中：张义军[4]基于实船测试数据综合分析船舶过闸的航行下沉量；谭志荣等[5]将最大吃水与定额吨进行拟合，提出过闸船舶吃水在某一区间内时的最优装载；KOOMAN[6]以船队进船闸的模型试验提出船队进闸时的水位变化回归模型。张松[7]在船模在受限水域数值分析的基础上，对该船模在浅水和深水航行条件下进行数值计算，分析船速、航道岸壁、浅水对下沉及纵倾的影响。张云鹏[8]分析影响船舶沿岸航行富余水深的影响因素，其中下沉量因素是不确定量，可通过水动力学理论分析得到船体下沉量区间。

1 船舶下沉量理论预报

1.1 schijf方法

该方法是在里斯本(1949年)和罗马(1953年)的PIANC大会上提出的，假设如下:(1)容器周围水位的降低是均匀的；(2)回流在航道截面上均匀分布；(3)忽略岸边和船上的摩擦以及所有损失；(4)适用于梯形截面的航道。基于流体力学的连续性方程和伯努利方程，构建在浅水航道通航船舶的下沉与回流计算模型，推理如下：

连续方程(简化版)为

伯努利方程(PIANC修订版)为

(2)

由式(1)和式(2)可化简得DAND & Ferguson公式：

(3)

(4)

令

则式(4)变换为一元三次方程y3+py+q=0,当式(5)成立时，用Cardan-Tartaglia公式求解：

δ=-(27q2+4p3)≥0

(5)

即在亚临界条件下(常规排水量型船舶)，式(4)有以下解：

回流速度u：

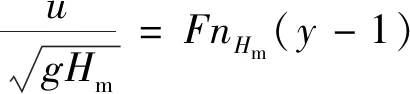
(6)

下沉量Zb：

(7)

式(6)和式(7)中：

对式(7)采用VB编程软件进行数值求解，如图1所示。下沉量Zb表达式为

图1 VB编程界面

(8)

1.2 schijf方法下沉量数值计算

影响schijf方法计算下沉量精度的主要因素之一是α的不同取值。将α的取值确定在(1，1.3)，将船舶下沉量的理论预报值与航宽为34 m的三峡船闸48艘实船测试值进行对比。VB编程计算的部分结果如表1所示。

表1 α取不同值时部分下沉量计算值

1.3 基于schijf方法的下沉量预报误差修正

采用schijf方法计算船舶下沉量时，假定船舶在浅水航道航行时船舶周围的流场变化是一致的。对船闸通航船舶而言，存在显著差异：(1)船闸中的流场呈现较强的非一致性动态变化(如：船闸冲/放水会产生非恒定流)；(2)船舶进闸航行时会产生船行波，在船闸前端的闸门会产生相应的反射波；(3)船闸是矩形截面，而schijf方法一般适用于梯形截面的航道；(4)船闸通航船舶存在较严重的岸壁效应，而schijf方法忽略岸壁效应。

因此，基于schijf方法计算船闸通航船舶的下沉量预报值难以确保预报精度，有必要通过船闸通航船舶下沉量的实测值开展下沉量预报误差分析，以提高船闸通航船舶下沉量预报精度。

采用统计分析软件SPSS对理论预报值开展非线性回归分析，采用2种误差回归模型。

1.3.1 独立参数下的多自变量误差回归非线性模型

将实测下沉量与schijf方法计算的下沉量相减得到的误差Rb1作为因变量，将堵塞率m和平均深度傅汝德数FnHm作为自变量。表2是α取不同值时，独立参数下多自变量误差回归非线性模型拟合优度。

表2 独立参数下多自变量误差模型拟合优度

由表2可知：

(1) 当α取1.30时，独立参数下多自变量误差模型的拟合优度最高，为0.92。该模型修正后的下沉量预报值与实测下沉量之间的均方根误差为3.260%，大于3%。48艘过闸船舶下沉量对比如图2所示。

图2 α=1.30时独立参数下多自变量误差模型修正下沉量与实测下沉量对比

(2) 当α取1.20时，独立参数下多自变量误差模型的拟合优度为0.87，均方根误差为2.998%，小于3%。48艘过闸船舶下沉量对比如图3所示。

图3 α=1.20时独立参数下多自变量误差模型修正下沉量与实测下沉量对比

综合考量，选取α=1.20时的独立参数下多自变量误差回归非线性模型为

(9)

其拟合优度为0.87。

1.3.2 组合参数下的单自变量误差回归非线性模型

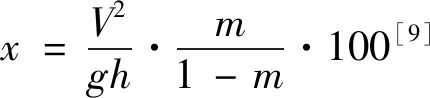
表3是α取不同值时，组合参数下单自变量误差回归非线性模型的拟合优度。

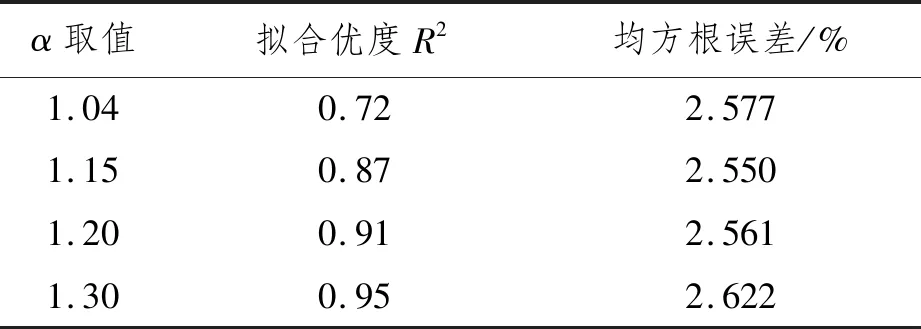
表3 组合参数下单自变量误差回归非线性模型拟合优度

由表3可知：当α取1.30时，组合参数下的单自变量误差回归非线性模型的拟合优度最高，为0.95，且修正后的下沉量预报值与实测下沉量之间的均方根误差为2.622%(小于3%)。48艘过闸船舶下沉量对比如图4所示。

图4 α=1.30时组合参数下单自变量误差模型修正下沉量与实测下沉量对比

综合考量，选取α=1.30时的组合参数下的单自变量误差回归非线性模型为

Rb2=0.0052-0.0034x-0.0399x2-0.0033x3

(10)

1.3.3 下沉量预报模型

综合考量，采用α=1.30时的组合参数下的单自变量误差回归非线性模型进行船闸通航船舶下沉量预报，模型为

Z预=Zb+Rb2

(11)

式中：Z预为基于schijf方法的三峡船闸下沉量预报值；Zb为schijf方法在α=1.30时计算的船舶下沉量；Rb2为组合参数下的单自变量误差回归非线性模型计算值。

2 结 论

将浅狭航道通航船舶的下沉量理论计算方法引入船闸通航船舶下沉量理论预报中。基于三峡船闸48艘通航船舶下沉量实测值，构建船闸通航船舶下沉量理论预报误差修正模型，提出三峡船闸通航船舶下沉量预报模型，为后期构建三峡船闸通航船舶航速与装载吃水的动态耦合模型奠定基础。