资产评估中城商行存款预测模型的选择与效果分析
2020-01-01袁国军
袁 杰,袁国军
(皖西学院 经济与管理学院,安徽 六安 237012)
当前,我国城市商业银行的资本实力大幅增强,资产规模迅速提升,同时,城商行也在积极的借助资本市场力量寻求快速发展的机会。截至2017年底,我国7家国内商业银行已在A股上市。至2018年初,成都银行也顺利登上A股市场。
可以看出,我国城市商业银行正在不断成长,城商行将不断涉及股改、股权转让、重组、IPO业务以及外资和民间资本进入银行业等事件。而合理的股权估值将成为这些资本活动的顺利开展的基础。
由于银行的特殊性,在进行股权价值评估时选取的估值方法时,很难套用普通企业的价值评估方法。因此,对于银行这种特殊的行业,在资产评估实务中选取普通企业的评估方法将造成较大的结果误差。因此,我国已有很多学者对于商业银行价值评估方法进行了探究,费亚群、李文卿运用EVA折现方法计算银行整体价值并与市场价值进行对比研究[1]。李斌运用收益法、成本法、市场法对商业银行对并购中商业银行的价值评估进行探究[2]。洪志军、谭跃、程锦将实物期权方法应用在银行并购价值评估中[3]。陈艳利、殷翠微从非上市城商行股权转让定价被高估状况出发,研究市场法在非上市城商行中的可行性[4]。可以看出,城商行的资产评估或价值评估研究,我国学者大多是从两个方向进行研究:一是,对资产评估中各种估值方法在商业银行价值评估方法的适用性进行对比研究。二是,某种方法在城商行资产评估中的可行性。在现阶段,根据查阅我国学者研究成果和已上市商业银行公告中披露的资产评估报告及说明显示,收益法在商业银行价值评估中使用较多,也得到国内学者一致认可[5-7]。对于收益法,在商业银行评估指导意见《资产评估专家指引第3号——金融企业收益法评估模型与参数确定》以及目前对商业银行价值评估研究中,均提及了存款预测的必要性和重要性,但两者均未提及如何对于存款量这一复杂的指标的预测方法。而在近期的商业银行资产评估说明与报告中,如2010年深圳发展银行股份有限公司拟平安银行股份有限公司整合项目评估报告,2015年南京栖霞建设股份有限公司收购河北银行8.75%股权项目评估说明,2014年江苏金智科技股份有限公司,拟转让所持有的江苏银行股份有限公司部分股权项目,2016年张家港银行及杭州银行首次公开发行股票招股说明书,也均未提及对于存款这一重要指标的预测方法。存款预测的合理性是银行整体评估值合理的前提条件,如何选择合适的存款预测模型是现阶段银行资产评估实务中亟待解决的问题。
因此,对我国的城商行估价中的应用进行进一步的研究,不但有助于完善我国城商行价值评估和价值管理理论体系,还有助于加强城商行管理者和资本投资者的决断能力,在我国产评估行业不断发展完善的今天,具有一定的现实意义。
一、资产评估中存款预测方法与预测模型的选择
城商行的吸收存款预测与其他经济预测一样,首选需要对预测模型进行选择,这是城商行存款预测的核心,也是价值评估中最为关键的部分。对于商业银行而言,经济因素、政治因素、法律因素以及政策因素等均会对存款造成不同的影响[8-9],如何选择合适的存款预测模型也是一项较为困难的工作。选择一个合理的存款预测模型,不仅需要对预测模型的特点、类型进行分析,还需要结合城商行评估的特殊性以及资产评估工作的具体情况,使得预测结果客观、可行和准确。
一般的经济预测可分为两类:定性和定量分析。其中,定性研究主要方法有德尔菲法、判断预测法、市场调查法、类推法等。定量研究方法主要运用计量统计方法,对数据资料进行分析,得到所需要的预测结果。预测模型还需结合计量经济学、数理经济学等理论方法。现阶段常用的预测模型主要有:线性回归模型、移动平均模型、趋势外推模型、灰色模型、ARIMA模型、投入产出模型以及神经网络模型[10]。
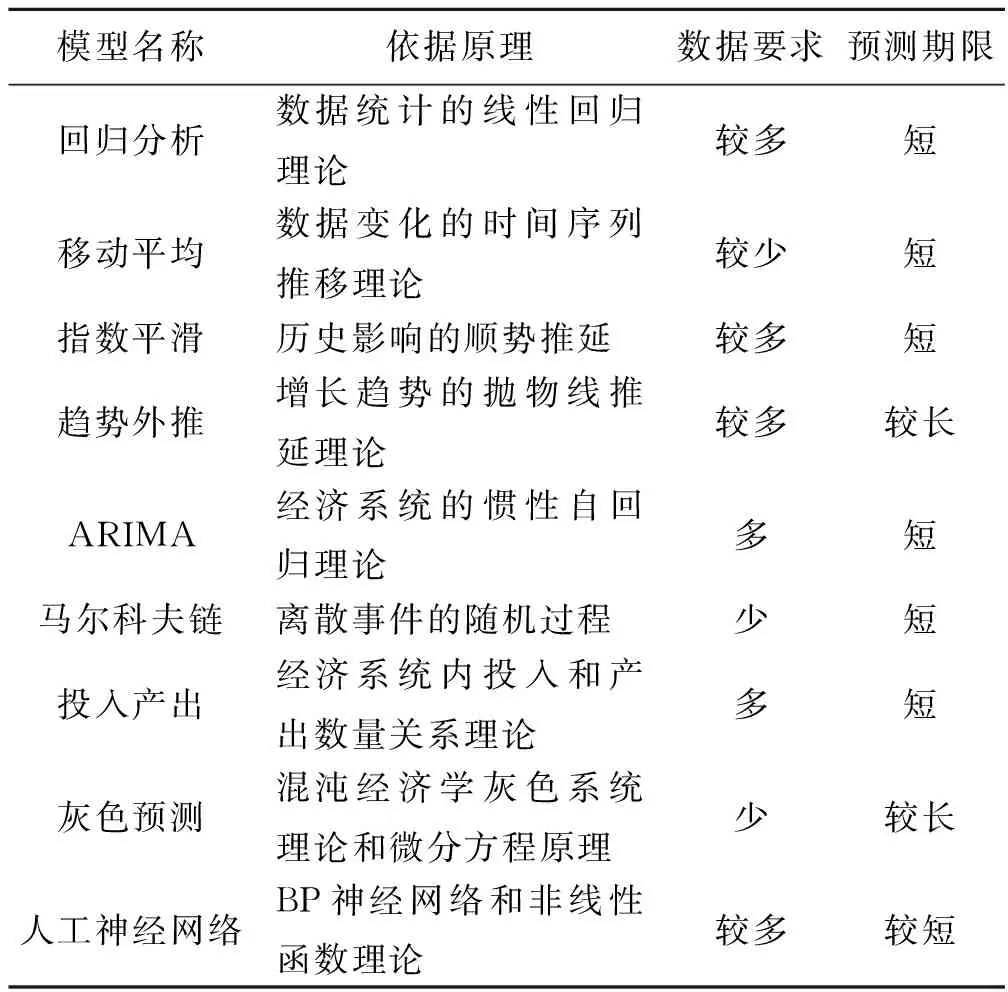
表1 预测模型对比分析
数据来源:笔者整理
如前文所述,存款预测是一个复杂的问题,不仅需要考虑经济因素、政治因素、法律因素以及政策因素等,还需要考虑银行所处区域以及银行自身状况。然而对于资产评估而言,运用少量的数据,即可进行准确且期限较长的预测,将成为城商行存款预测模型的首选。
然而,灰色理论是基于小样本和不良信息不确定性系统。以提取有价值的信息,实现进化规律的正确模拟,并用少量数据实现定量预测[11]。可以看出,银行存款的复杂与不确定性,以及资产评估中可能存在的样本缺乏,信息缺乏等情况,也正是符合灰色模型的理论基础。
因此本文考虑灰色模型中的EGM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)、Verhulst灰色模型对城商行的吸收存款数据进行适用性及预测效果分析。
二、资产评估中存款预测模型构建
由于存款量是等时等间距的,因此常用的单阶单变量的预测模型有EGM(1,1)、ODGM(1,1)、EDGM(1,1)和DGM(1,1)模型等。
(一)GM(1,1)模型
根据历年银行存款量X(0)=x(0)(1),x(0)(2),x(0)(3),…,x(0)(n),X(1)为X(0)的1-AGO序列,则X(1)=x(1)(1),x(1)(2),x(1)(3),…x(1)(n)。而Z(1)=z(1)(2),z(1)(3),z(1)(4),…,z(1)(n)为X1的紧邻均值生产序列。
其中
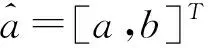
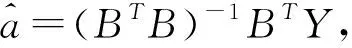
(二)ODGM(1,1)模型
(三)DGM(1,1)模型
DGM(1,1)模型是GM(1,1)模型的一种离散的形式,其建模的过程与GM(1,1)模型是基本类似的,只是DGM(1,1)的模型参数序列为β=[β1,β2]T,且矩阵B与矩阵Y变更为一下形式:
则β=(BTB)-1BTY。从而,DGM(1,1)模型为:
x(1)(k+1)=β1x(1)(k)+β2
(四)EDGM(1,1)模型
EDGM(1,1)模型是GM(1,1)模型的一种均值估计参数模型,是以x(0)(k)+az(1)(k)=b均值差分方程式的解当做响应式而得到的模型称为均值差分的GM(1,1)模型。
(五)灰色Verhulst模型
灰色verhulst模型是依据生物演化繁殖、人口变化等特征对malthusian进行整合,并入一个发展的限制项得到以下的verhulst模型[12-13]:
Verhulst模型首先根据原始符合样本数据序列x(0)分别得到一阶累加(1-AGO)新数据序列x(1)以及紧邻均值生成序列Z(1)。建立灰色Verhulst模型微分方程为:
式中,a,b为参数项,其最小二乘估计为
A=[a,b]T=(BTB)-1BTY
式中
从而灰色Verhulst模型为:
x(0)(k+1)=x(1)(k+1)-x(1)(k),(k=0,1…)
三、资产评估中存款预测模型的效果分析
(一)数据选取
选取银行存款总量数据主要源于wind资讯搜集上市城市商业银行2007—2016年年报,选取A股上市的城市商业银行吸收存款数据。如表2。
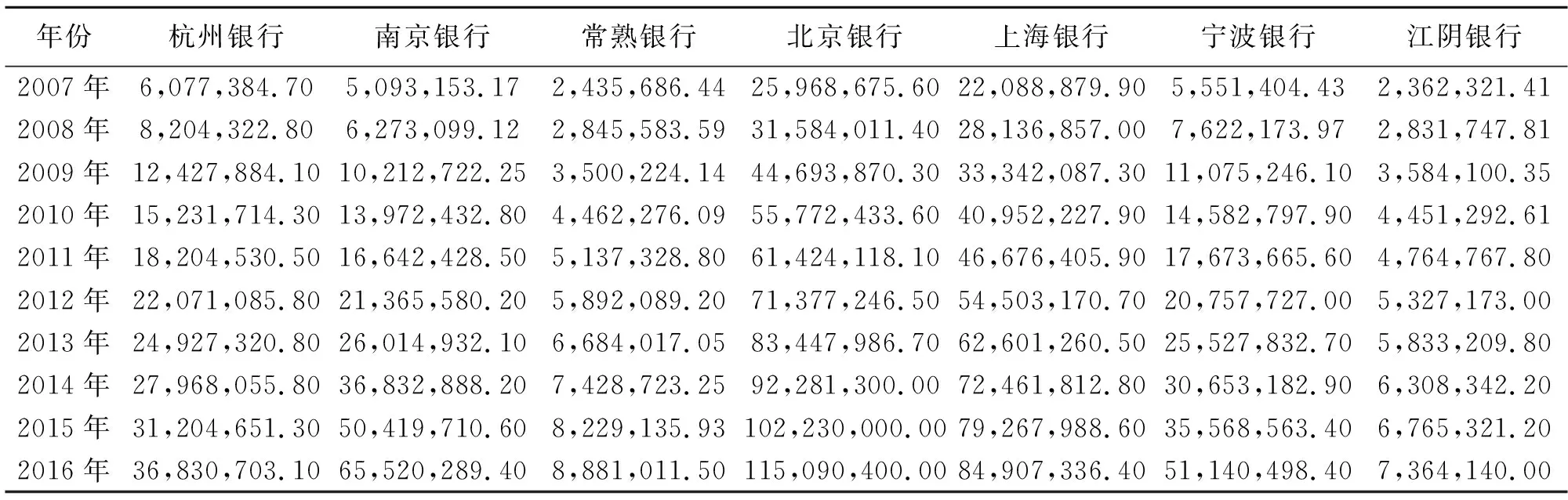
表2 2007—2016年城商行吸收实际存款量 金额单位:人民币万元
数据来源:笔者整理
(二)模型适应性分析
根据各银行年报中吸收存款量得到2007—2016年各城商行吸收存款的原始数据,运用灰色模型进行模拟,其模拟值见表3—表5,由于篇幅所限,只列举杭州银行、上海银行、宁波银行。
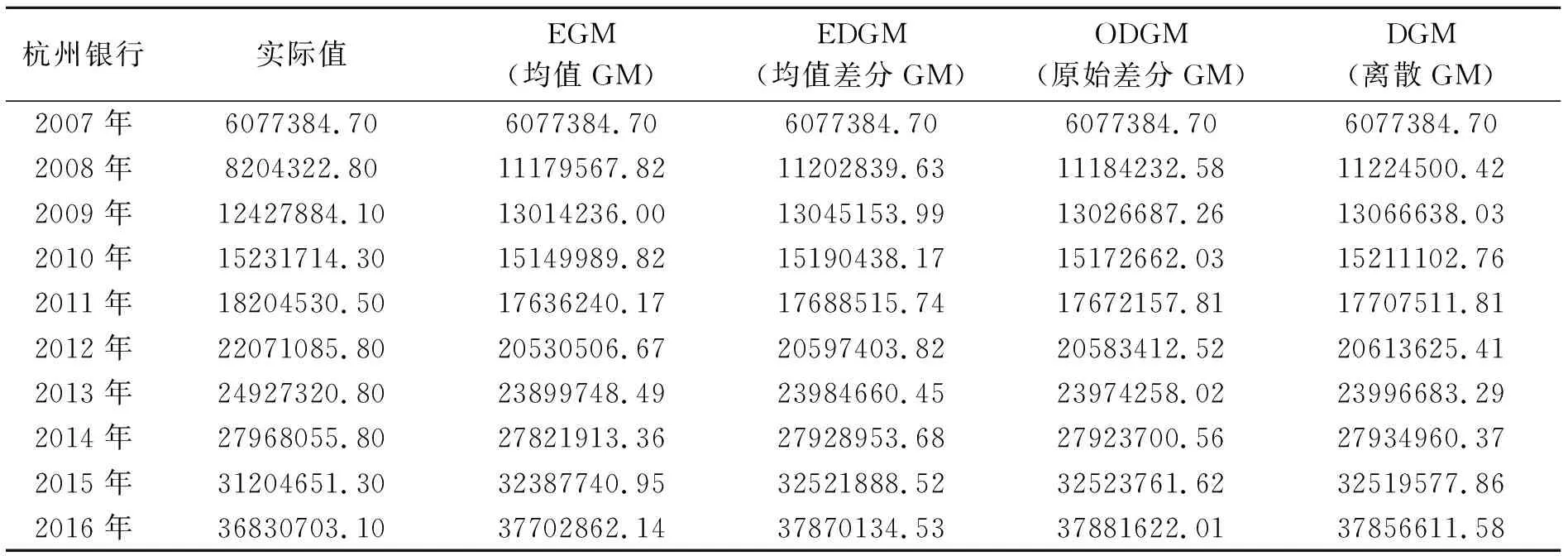
表3 杭州银行模拟值与实际值对比分析 金额单位:人民币万元
数据来源:笔者整理
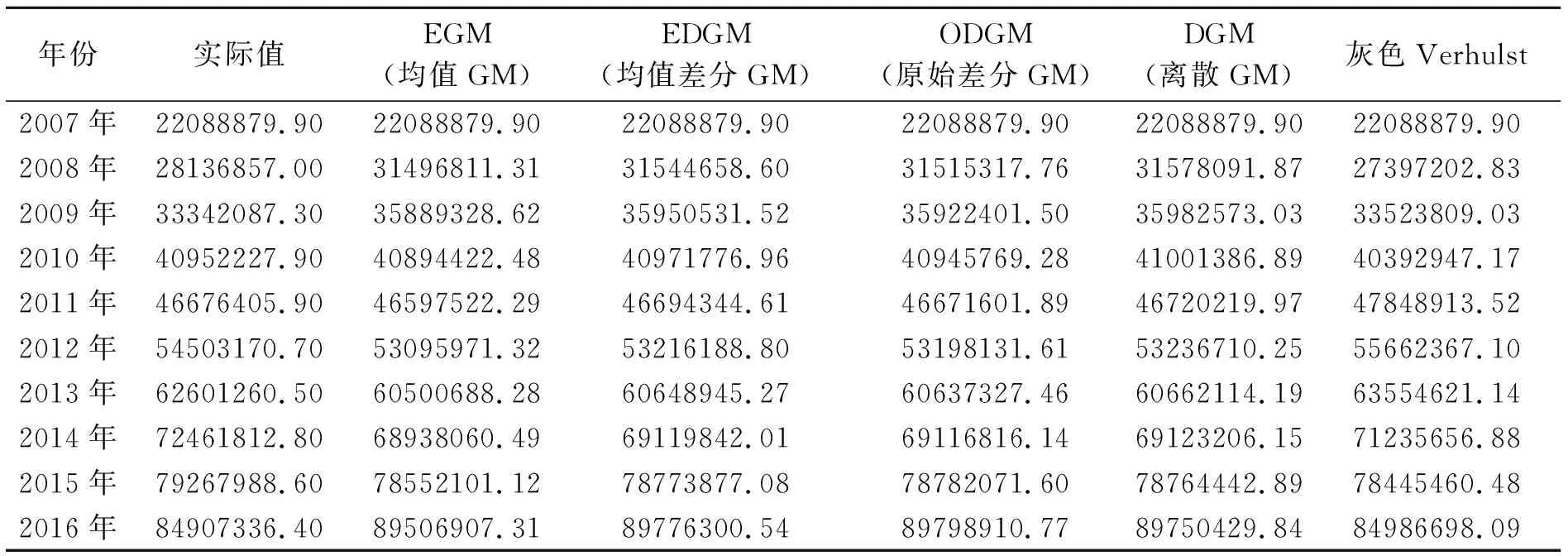
表4 上海银行模拟值与实际值对比分析 金额单位:人民币万元
数据来源:笔者整理
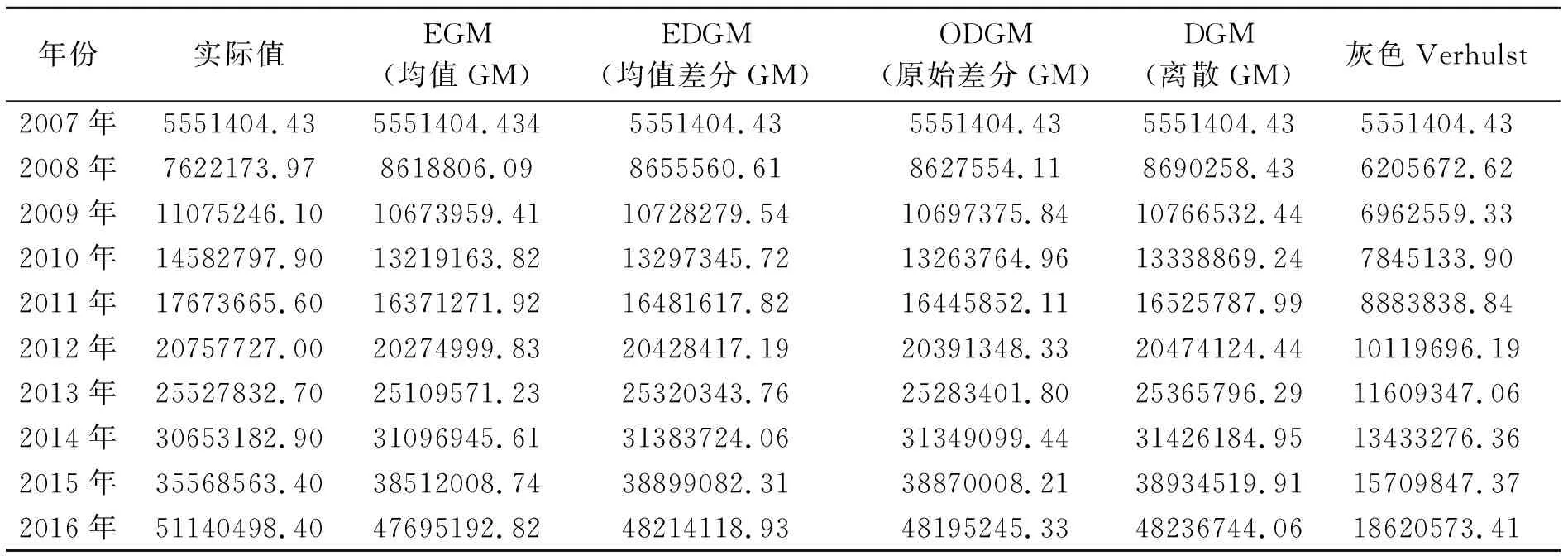
表5 宁波银行模拟值与实际值对比分析 金额单位:人民币万元
数据来源:笔者整理
(三)模型精度分析
对上述模型进行精度比较。主要为残差、相对误差、平均相对误差、残差平方和,其公式依次为:
在此次模型中,主要选择相对误差,平均相对误差对模型的精度进行比较。
7家城商行,EGM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)和Verhulst灰色模型的精度及误差值统计,见表6。
根据表6,可知,对于我国城商行的吸收存款量而言,EGM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)和Verhulst灰色模型的预测精度从小到大依次为,Verhulst 表6 城商行相对误差对比分析 数据来源:笔者整理 本文通过分析现阶段常用的经济预测模型,考虑到资产评估业务及银行存款量的特殊性,建立EGM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)和Verhulst灰色模型,分别对杭州银行、南京银行、常熟银行、北京银行、上海银行、宁波银行、江阴银行,2007—2016年年报所列吸收存款量进行分析,得到如下结论: 1)银行吸收存款预测的复杂性与不确定性,以及资产评估实务中,样本缺乏,信息贫瘠,符合灰色模型的理论基础。但由于多种灰色模型不同的特点,在预测时所得到的所得到的误差精度检验结果各不同,因此,进一步解释了在实际应用模型时精度测试的重要性。 2)对于资产评估业务中城商行吸收存款预测而言,Verhulst模型稳定性较差,灰色模型拟合精度排序为:Verhulst 3)在资产评估实务中,可以选取DGM模型,与城市商业银行战略规划,以及银行业监管指标相结合对银行存款量进行预测。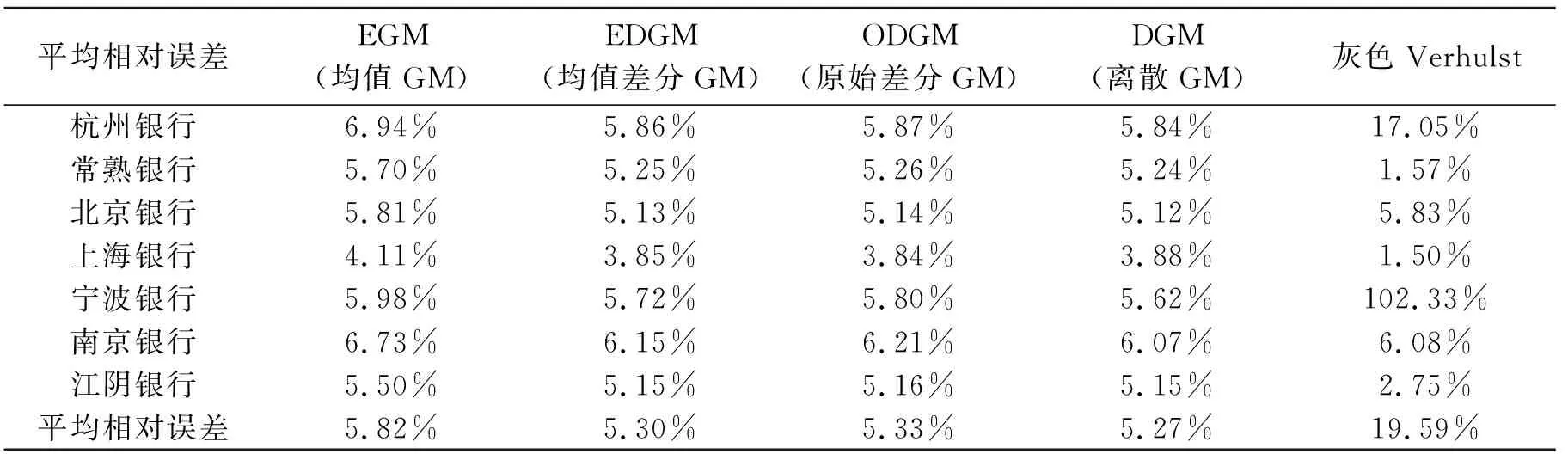
四、结论
