增程器轴系平行不对中故障诊断特征研究*
2020-01-01吴强
吴 强
(武汉交通职业学院,湖北 武汉 430065)
在能源枯竭和环境污染的大环境下,各汽车企业都在研究和开发新能源汽车,而增程式电动汽车就是其中一个重要研究方向。
增程式电动汽车依靠增程器和动力电池组作为能量来源,增程器含有发动机和发电机两大部件,组成长轴系系统,在增程器轴系旋转系统的常见故障中,不对中故障是其中之一。从相关资料了解到,旋转系统所发生的常见故障中有超过60%是不对中故障所诱发的[1],不对中故障常常会引发碰磨、裂纹、油膜失稳等。增程器轴系旋转系统由于有着高效率、高性能的要求,使得在设计制造时转子与轴承间的间隙越来越小,进而使旋转系统发生故障的可能性大大增加。对于不对中故障,诸多学者开展了研究。徐福泽建立了单一转子系统不对中有限元模型,在转子动力学分析软件DyRoBeS 中,通过NewmarK-β数值积分法求得了不对中故障的振动特性,得到了诊断特征[2]。太兴宇建立了单跨式转子系统的不对中动力学模型,通过改变不同的状态参数,对转子系统的不对中故障进行了仿真分析[3]。许小伟建立了增程器轴系动力学模型,利用多体动力学软件仿真,分析了不同类型不对中故障产生的动力学响应特性[4]。以往的研究主要集中在简单的单一轴系系统,但增程器轴系旋转系统具有较复杂的轴系结构,故障变化较简单单一轴系系统更加复杂,不能用普通轴系系统模拟。也有学者即使探索了增程器故障特征,却没有对故障特征的出现进行分析,也未对其准确性进行进一步的验证。而如果直接实物设置故障,再采集相关数据进行故障特征提取,则会损坏增程器,更甚者有危害于试验人员,故此种方法也有一定的限制性[5]。
研究增程器轴系系统不对中故障诊断特征对于增程器故障检测分析具有重要意义,且同时借助虚拟样机技术进行多体动力学仿真,可节约成本、缩短实验时间和保证研究安全,可对机械系统多种可能出现的故障进行模拟[6]。
故本文通过建立增程器轴系虚拟样机刚柔混合模型,以研究具有高发性的平行不对中故障为目标,对多工况进行仿真分析,提取了平行不对中故障诊断特征,并对故障特征进行机理分析,再利用小波分析,对提取的故障特征的准确性进行验证,以此为增程器轴系平行不对中故障的诊断提供依据。同时,也由此探索了一种结合多技术的故障诊断特征研究方法,可借鉴于诊断增程器其他故障。
1 增程器多体动力学刚柔混合模型的建立
本文研究的增程器是一款额定功率为24kW的特定型号增程器,根据内燃机和发电机设计标准,设计计算得到了增程器各零部件的基本尺寸。统筹使用三维CAD 软件CATIA、有限元软件ANSYS 和多体动力学虚拟样机软件ADAMS:在CATIA 中建立了增程器各部件三维实体模型,并将各部件组装成整个增程器轴系系统三维模型;在ANSYS 中对曲轴等部件进行了强度分析和模态分析,验证了零部件的设计要求,并建立了柔性曲轴;在ADAMS中导入增程器轴系系统三维模型和柔性曲轴,根据增程器轴系系统实际构造特性,对相关部件的材料属性、运动副、连接关系、外部激励和驱动进行设置。得到的增程器轴系系统多体动力学刚柔混合模型如图1所示。

图1 增程器轴系系统多体动力学刚柔混合模型
2 增程器不对中故障特征参数提取
考虑多不对中工况研究,本文模拟仿真了4组不对中故障工况:不对中Δ0 为0mm 的正常工况、不对中Δ1 为0.5mm 的轻微不对中工况、不对中Δ2 为1mm 的中度不对中工况以及不对中Δ3 为2mm的严重不对中工况。
2.1 额定转速工况下不对中故障仿真分析
不对中故障将导致增程器转子出现上下或者左右振动[3],同时兼具在增程器上添加传感器测量的可行性考虑,通过对大量数据特征进行分析,拟从转子的质心振动入手探索故障诊断特征。
2.1.1 不对中故障下时域分析
图2 为Δ0、Δ1、Δ2 和Δ3 工况下的转子振动时域图。可以发现,当发生不对中故障,正常与故障工况下的转子振动时域曲线相差不大,仅仅是在波动范围上有微小差别,即随着不对中值的增大,时域曲线波动也变大。这是因为不对中故障会使转子在轴承中跳动,从而导致振动波动变大。
时域信号对不对中故障有一定的描述作用,但不足以作为故障特征。

图2 多种不对中值工况下的转子振动时域曲线
2.1.2 不对中故障下转子振动频域分析
将各种不对中工况下的转子振动信号通过FFT 快速傅里叶变换得到转子振动频谱图。在经过滤波处理后得到不对中值为Δ0、Δ1、Δ2和Δ3下的四种工况频谱图,如图3所示。
观察图3(a)可以发现,在Δ0不对中值的正常工况下,转子振动频谱图中表现出了1.0倍转频分量的频率特性,这与四冲程内燃机的增程器在运转过程中会出现1.0 倍转频分量的理论相符。继续观察图3(b)、(c)和(d)可以发现,伴随着不对中故障的产生,频谱图中由Δ0 工况的只有1.0 倍转频分量,变化为Δ1、Δ2 和Δ3 工况下的1.0 倍转频、2.0倍转频和3.0倍转频与4.0倍转频的高次分量的组合,但主要以1.0 倍转频和2.0 倍转频为主要振动频率分量,且随着不对中值的增大,1.0 倍转频和2.0 倍转频分量振动加剧,即1.0 倍转频和2.0倍转频分量幅值增加。
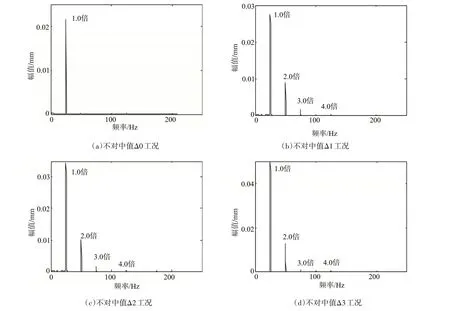
图3 转速1500rpm各种平行不对中值下转子振动频谱图
2.2 其他转速工况下不对中故障仿真分析
为进一步研究不对中故障在不同转速下对转子系统的影响特性,取转速分别为1000rpm 和2000rpm 继续进行仿真分析。图4 和图5 分别为转速1000rpm 和2000rpm 下的各种不对中值工况的转子振动频谱图。
观察图4和图5可以发现,所呈现的频谱规律与额定转速下的规律相同,即正常工况下,频谱中只表现了1.0 倍转频分量;不对中工况下,频谱中还出现了2.0 倍转频等高阶响应,随着不对中值Δ增加,1.0倍转频和2.0倍转频分量响应加剧。
2.3 仿真结果总结及故障特征提取
为全面分析转子振动频谱随不对中故障的变化规律,做出多种转速下转子振动频谱随不对中值响应的三维瀑布图,如图6所示。
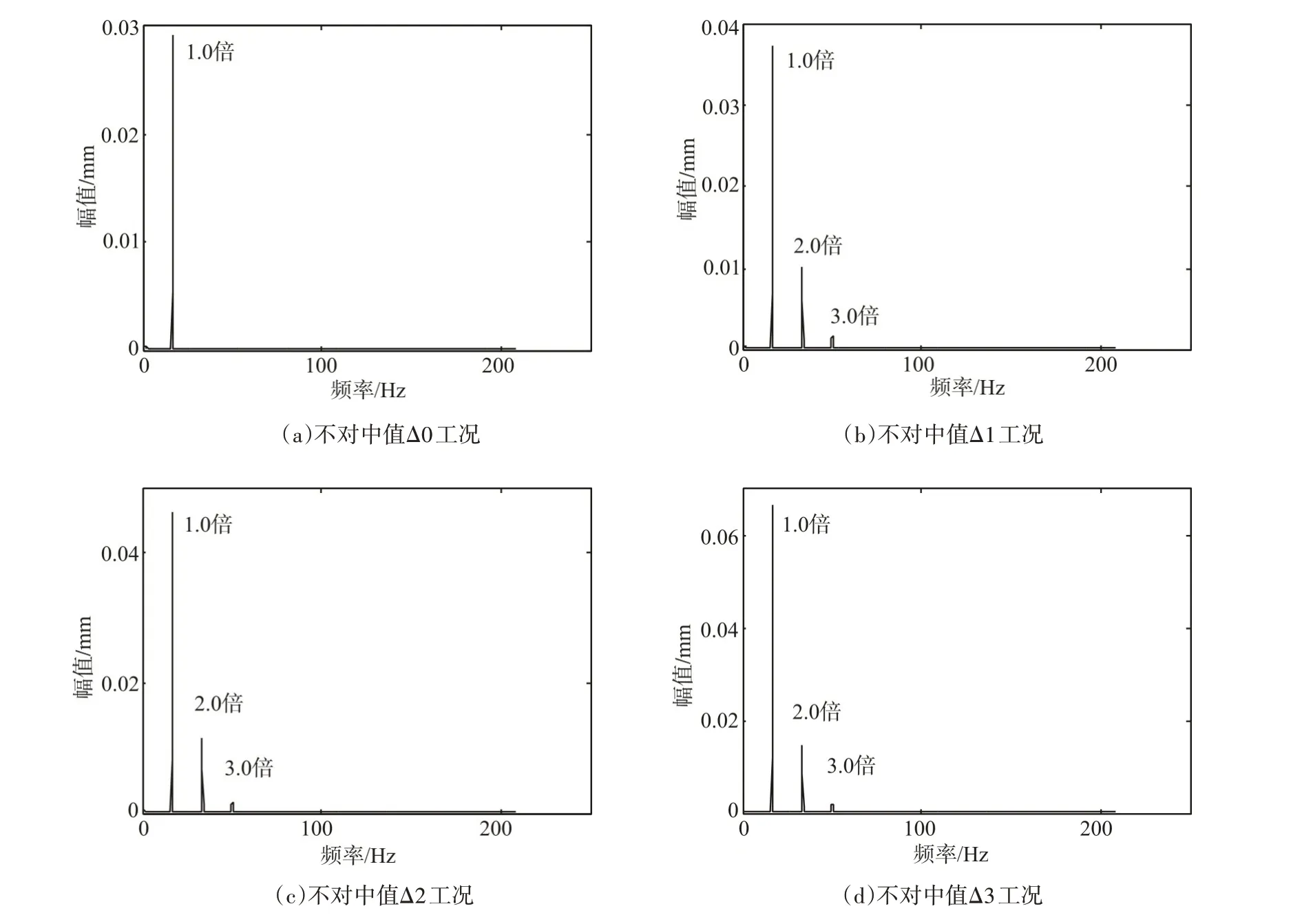
图4 转速1000rpm各种平行不对中值下转子振动频谱图

图5 转速2000rpm各种平行不对中值下转子振动频谱图
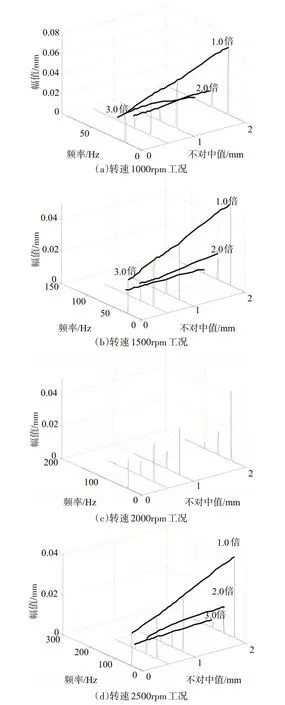
图6 多种转速工况下转子振动随不对中值响应瀑布图
(1)在各个瀑布图中,不对中值Δ0 工况的频谱图只历经了1.0 倍转频的瀑布帘,即只有1.0 倍转频分量特性;不对中值Δ1、Δ2 和Δ3 工况的频谱图历经了多条瀑布帘,即表现了多种频率成分的组合。
(2)不对中值Δ1、Δ2 和Δ3 工况下频谱图随不对中值的增大,1.0 倍转频和2.0 倍转频分量的瀑布帘不断上流,即不对中值越大,1.0 倍转频和2.0倍转频分量振动越明显。
为对所呈现出的倍频值规律进行具体量化,列出转速分别为1000rpm、1500rpm、2000rpm 和2500rpm 下各工况的1.0 倍转频分量和2.0 倍转频分量幅值如表1所示。

表1 多转速、多不对中值工况下特定倍频分量幅值
结合表1 的数值量化规律发现:任意转速下,不对中故障的产生都会促使1.0倍转频和2.0倍转频分量的增加,且不对中值越大,分量增加越多。表1所呈现的倍频值规律与振动频谱图相一致。
因此,结合上述研究,可以以转子振动1.0 倍转频分量和2.0 倍转频分量作为增程器轴系平行不对中故障的诊断特征。
3 平行不对中故障机理研究分析
当联轴器转子间出现平行不对中时,转子的轴线间会有了平行偏移,会在转子上产生径向力和轴向力。图7 为联轴器平行不对中时的受力图,两半联轴器的平行不对中量为Δ,结合在P点,主动转子和被动转子的旋转中心为O1 和O2,转子的角速度为ω,则联轴器上P点的转角为ωt。

图7 联轴器平行不对中受力图
转子系统在旋转运动时,不同心的两转子的轴心因受到螺栓力作用,两轴会往中心靠拢。因结合点P到两转子中心的距离为被动轴大于主动轴,即PO2>PO1,故在主动轴上产生压力,被动轴上产生拉力[6]。在PO2 上取一点A,且有PO1=PA。通常情况,不对中量Δ较小,可以近似地认为O1A垂直于PO2,则有:
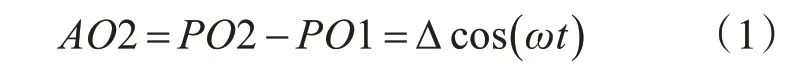
可近似认为两半联轴器变形相等,即有:
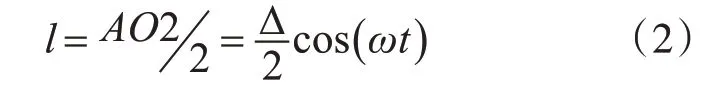
设主动轴的刚度为K,则主动轴上的压缩力和被动轴上的拉伸力为:
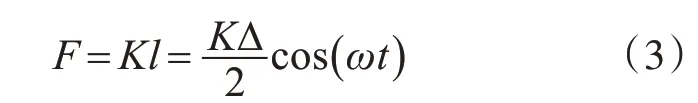
将轴上力F沿水平方向和竖直方向分解为FX和FY:

式(4)中,FX表示水平方向上有2 倍于转速变化的激振力,FY的第一项KΔ/4 为两轴间的拉力,其为定值,第二项KΔcos(2ωt)/4 表示竖直方向上有2 倍于转速变化的激振力。因在水平和垂直方向存在2 倍于转速变化的激振力,即转子系统旋转一个周期,径向力会交变两次,径向方向上会产生2.0 倍转频为主的振动分量特征。同时经过相关研究发现,除了会表现2.0 倍转频特征外,还时常出现1.0 倍转频特征分量。由式(4)可知,不对中导致的激振振动会随着不对中值Δ的增加而加剧。
由故障机理可知,仿真出现2.0倍转频分量正如对不对中故障机理研究中所提到的,平行不对中故障会出现2倍于转速变化的2ωt激振力,从而引发2.0 倍转频的特征分量;仿真发生1.0 倍转频分量的增大,则是因为平行不对中故障拥有转频特征频率;仿真同时伴有3.0 倍转频和4.0 倍转频等高阶分量,是因为转子系统在振动过程中由于转频的波动,除了出现1.0 倍转频和2.0 倍转频分量,还会出现高倍频作为常伴频率[7]。
由此可知,仿真得到的结果与故障机理理论研究分析基本一致。因此,结合上述仿真和机理研究,可以进一步确定以转子振动1.0倍转频分量和2.0 倍转频分量作为增程器轴系平行不对中故障的诊断特征。
4 不对中故障特征的小波分析
通过多体动力学仿真分析,提取了转子振动频谱中1.0倍转频和2.0倍转频分量的增程器轴系平行不对中故障诊断特征。为对由此方法获得的故障诊断特征的准确性进行验证,可使用小波分析技术的分解与重构功能[8]来进行验证。借助小波分析频带分离技术,频率信号被分解到不同频带上,由此得到1.0 倍转频和2.0 倍转频在相关频带内细节信号,进行信号响应的分析。利用sym3小波对额定转速1500rpm 下的转子振动信号进行3层小波分析,得到各层信号如图8所示,其中s为源信号,d1 到d3 为高频信号,a3 为低频信号。根据采样定理,1.0 倍转频和2.0 倍转频分别在a3 和d3层。
观察图8 可发现,随不对中值增加,1.0 倍转频和2.0倍转频所在频带内的信号波动逐渐变大,这验证了前文研究得到的不对中故障会引起1.0倍转频和2.0倍转频分量振动加剧的结论,从而验证了所得的故障诊断特征的正确性。随不对中值的增加,2.0倍转频所在频带内信号振动波动大于1.0倍转频所在频带内的信号振动波动,这验证了前文机理研究中提到的平行不对中故障的故障特征主要为2.0 倍转频,1.0 倍转频特征只是其伴有特征频率。1.0倍转频和2.0倍转频分量频带内信号表现出一定的周期性,这说明转子系统不对中故障是周期性出现的。
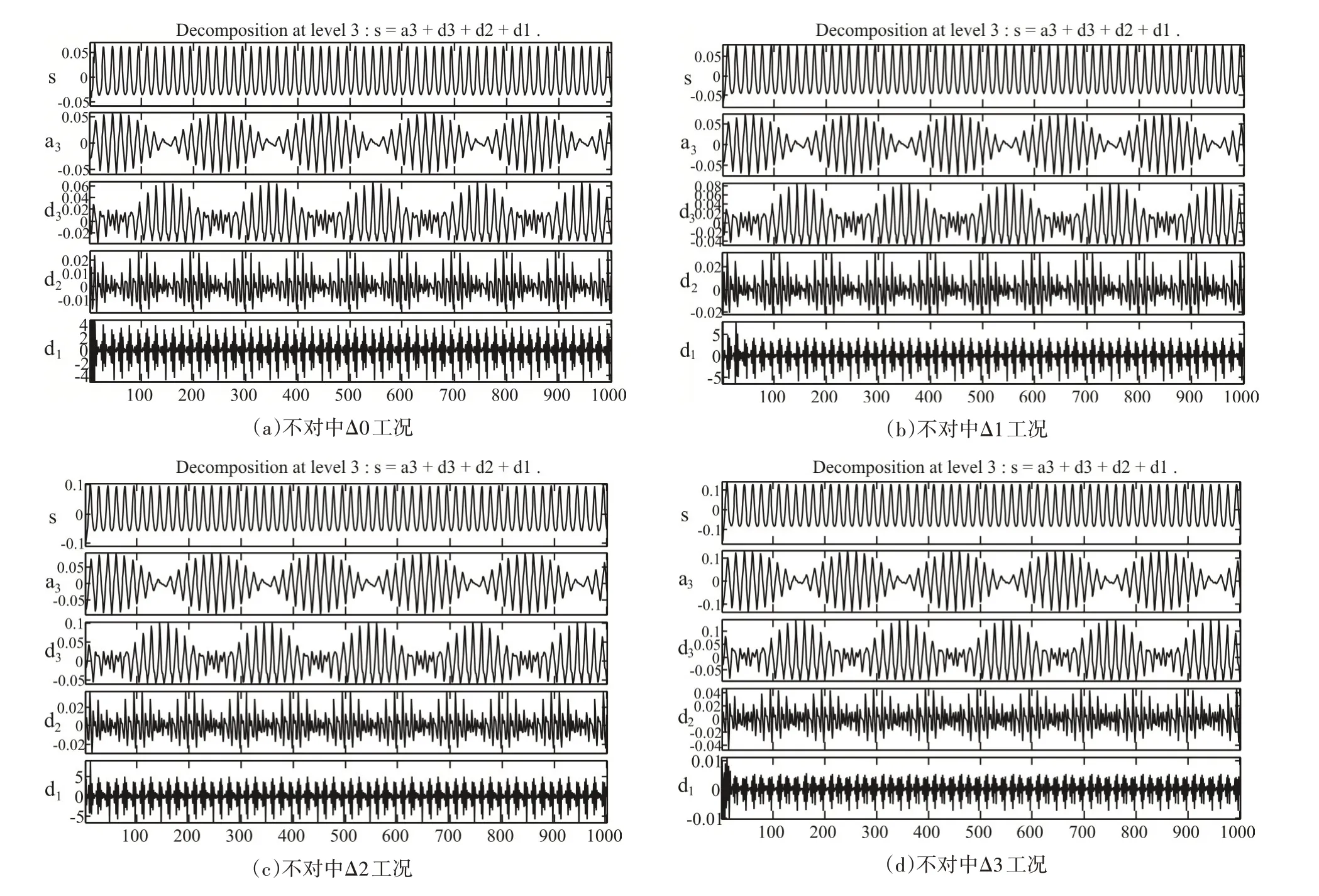
图8 转速1500rpm多种不对中值工况下小波分解
5 结论
在虚拟样机中搭建了增程器轴系系统多体动力学刚柔混合模型,通过多工况仿真分析,获取了平行不对中故障诊断特征,再结合小波分析,对诊断特征准确性进行验证。可以得出以下结论。
(1)通过仿真,结合机理研究,可将增程器轴系系统转子质心振动频谱的1.0转频和2.0倍转频分量作为增程器轴系系统平行不对中故障诊断特征。
(2)利用小波分析的频带分离技术,3 层分解了所提取的故障诊断特征,由于1.0倍转频所在的a3层信号和2.0倍转频所在的d3层信号的波动有逐渐变大的趋势,则对该故障诊断特征的准确性进行了验证。
(3)由此探索的一种结合多技术的故障特征诊断方法,可借鉴于诊断增程器其他故障。
