基于ARIMA-PCR模型的福建省物流需求预测
2020-01-01黄建华陈严铛卢箫扬
黄建华,陈严铛,卢箫扬
(福州大学 经济与管理学院,福建 福州 350108)
区域物流需求预测在完善物流规划、推动地区经济发展、实现物流资源合理配置等方面发挥着重要作用,受到地方政府和学界的广泛关注。2003—2018年,福建省货运量年平均增长率为10.42%,高于全国的年平均增长率(8.45%)。然而受区域经济发展水平、区域贸易、区域产业结构等多种区域因素的影响,福建省物流需求增长呈现非线性增长趋势,增幅波动大于全国平均水平,这增大了物流需求预测指标选取和预测方法选择的难度。单个计量模型在处理多指标的高维度时间序列问题时,预测效果不佳,因此,如何有效地选取预测指标和提高物流需求预测精度是福建省政府制定物流发展规划和经济发展计划的重要内容,也是目前福建省物流领域研究的热点[1]。
在物流需求预测指标选取上,大致分为综合指标和细分指标,有关综合指标的研究主要是选取货运量、交通运输量等单因素自相关指标进行预测[2-3],取得了较好的预测效果。但单一指标忽略了其他影响因素的作用,将增加物流需求预测的不确定性。细分指标通过分析多因素的相互作用很好地克服了上述问题,但选取哪些指标成为关键。后锐等[4]运用MLP神经网络方法揭示了区域经济与区域物流需求之间的映射关系,为区域物流需求指标选取提供了新思路。栾维新等[5-6]在此基础上,引入GDP、进出口总额、固定资产投资额、三次产业产值等多种经济因素对物流需求量进行预测,降低了物流需求预测误差。但上述研究存在以下不足:指标选取的主观随意性较大,指标构建框架不一,结果缺乏可泛化性和可比性;选择多样化的指标会增大模型的复杂度,且各指标间容易存在共线性问题,若不进行降维处理则容易产生伪回归现象,使预测结果并非最优。
在物流需求预测方法选择上,现有方法主要分为两类,即时间序列线性预测和非线性预测。传统的时间序列预测方法,如指数平滑法[7],由于数据易受异常值影响,预测误差较大。王红瑞等[8]将自回归和移动平均组合,形成新的时间序列预测方法,但该研究建立在数据是平稳的、无趋势的假设基础上,这使得该方法在处理波动数据时存在局限性。CHEN等[9]通过运用ARIMA模型将自回归移动平均法推广到非平稳序列中去,使预测模型的灵活性得到提高。葛娜等[10]通过对时间序列的原始数据进行预处理、模型识别与定阶、参数估计等步骤,建立ARIMA预测模型,结果表明所建立的ARIMA模型能较好地描述需求的变化趋势,但单个ARIMA模型无法体现出其他因素的作用,预测结果不确定性大。WANG等[11-12]则将时间序列ARIMA模型与神经网络算法相结合构建了组合预测模型,提高了预测精度,然而神经网络基于大样本数据,且对模型参数选择敏感[13-14],方法运用不当会加大预测误差。主成分回归法(PCR)将多个指标用线性组合的方式转化为少数相互正交的新变量,可以避免单一ARIMA模型预测不确定性大和神经网络参数选择敏感的问题,在指标遴选和数据降维方面具有很强的适用性[15-16]。IMANI等[17]将PCR引入ARIMA模型进行预测,经检验所构建的模型能合理预测里海海平面数据。MALLICK等[18]运用多个ARIMA-PCR模型预测印度市场不同期限利率的收益率及各利率间的相互作用,研究取得了良好的预测效果。目前关于ARIMA-PCR模型的研究较多集中于自然科学与经济学等领域的预测,尚未有学者将ARIMA-PCR模型应用于物流需求预测研究,考虑到福建省物流需求具有影响因素多、数据呈时序性等特征,选取单个ARIMA模型无法体现出其他因素的作用。若同时对多个指标分别建立ARIMA预测模型,再将各指标的预测结果运用PCR进行有机结合,则可有效提高预测的精度和预测结果的稳定性。因此,笔者从指标选取和预测方法选择两个角度出发,构建基于ARIMA-PCR模型的福建省物流需求预测模型具有一定的理论和现实意义。
1 福建省物流需求指标体系构建
物流需求是派生性需求,物流需求量受到多种因素的影响和制约。以福建省1981—2017年的统计数据为基础,从多维度选取影响因素,并运用相关分析[19-20]检验已选指标的合理性,筛选出数量少、相关性高的影响因素构建指标体系。
1.1 指标选取
考虑到指标的可量化性,结合国内外研究现状,用货运量表示物流需求量,分别从区域经济发展水平、区域贸易和区域产业结构3个维度选取影响因素,构建指标体系。
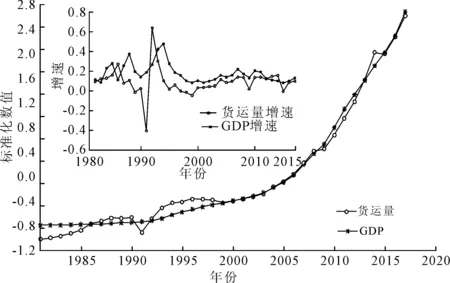
图1 1981—2017年福建省货运量与GDP数据对比
(1)区域经济发展水平。区域经济发展速度越快、规模越大、效率越高,经济发展水平越好,则物流需求量就越大。1981—2017年福建省GDP与货运量经标准化处理后的数据对比如图1所示,可知两组数据随时间变化的趋势非常接近,用简单的线性回归方法得到货运量与GDP的相关系数为0.995,回归方程拟合程度R2为0.987,说明简单线性回归方程拟合程度好,两指标存在强线性相关关系。但GDP并不是决定地区物流需求量的唯一因素。福建省货运量增速的变化幅度明显大于GDP增长的变化幅度,说明物流需求并不只受GDP因素的影响,还与其他因素如固定资产投资额、工业总产值等有关。
(2)区域贸易。区域贸易包括对内贸易和对外贸易,主要指标有社会消费品零售总额、进出口贸易额等。据福建省统计局数据分析可知,2018年福建省全年社会消费品零售总额达14 317.43亿元,较上年增长10.8%,全年进出口总额为12 354.30亿元,同比增长6.6%。区域贸易成为福建省区域经济发展的重要组成部分,区域贸易活动有力促进了福建省物流需求的增长。
(3)区域产业结构。区域物流需求来源于区域经济社会各个产业,是对区域内初始品、半成品、成品的多重测度,涉及经济活动的全过程,需要各产业结构的可量化指标,即第一产业产值、第二产业产值、第三产业产值。
1.2 数据来源及指标体系构建
为了检验所选指标是否合理,选取常用的Pearson相关系数法[21-22]检验变量间的相关程度和显著性水平,由式(1)计算变量间的相关系数r。
(1)
货运量与各指标相关性分析如表1所示,可知各项指标与货运量之间的Pearson相关系数均在0.950以上,且均在0.001水平下显著,表明所选指标与物流需求存在显著的相关关系,可有效预测福建省物流需求。基于此,构建福建省物流需求量影响因素指标体系,如表2所示。各指标原始数据如表3所示,数据来源为福建省统计年鉴。

表1 货运量与各指标相关性分析
注:***表示P<0.001
2 基于ARIMA-PCR的福建省物流需求预测模型构建
ARIMA模型是时间序列方法的一种变形,是将差分、自回归、移动平均方法组合起来,基于历史数据进行预测,在短期区域物流预测中具有较高的精度。运用多个ARIMA模型可以综合考虑多因素的作用,增加预测稳定性。考虑到各指标间的交叉、重叠或相互共线的问题,需对指标进行降维。PCR方法是在损失少量原有信息的前提下,将多个指标用线性组合的方式转换为相互正交的少数主成分变量,并进行主成分回归,在降低模型复杂度和减少共线性问题上应用广泛。因此,针对福建省物流需求的特征,构建ARIMA-PCR模型对物流需求进行预测,建模流程如图2所示。

表2 物流需求量影响因素指标体系
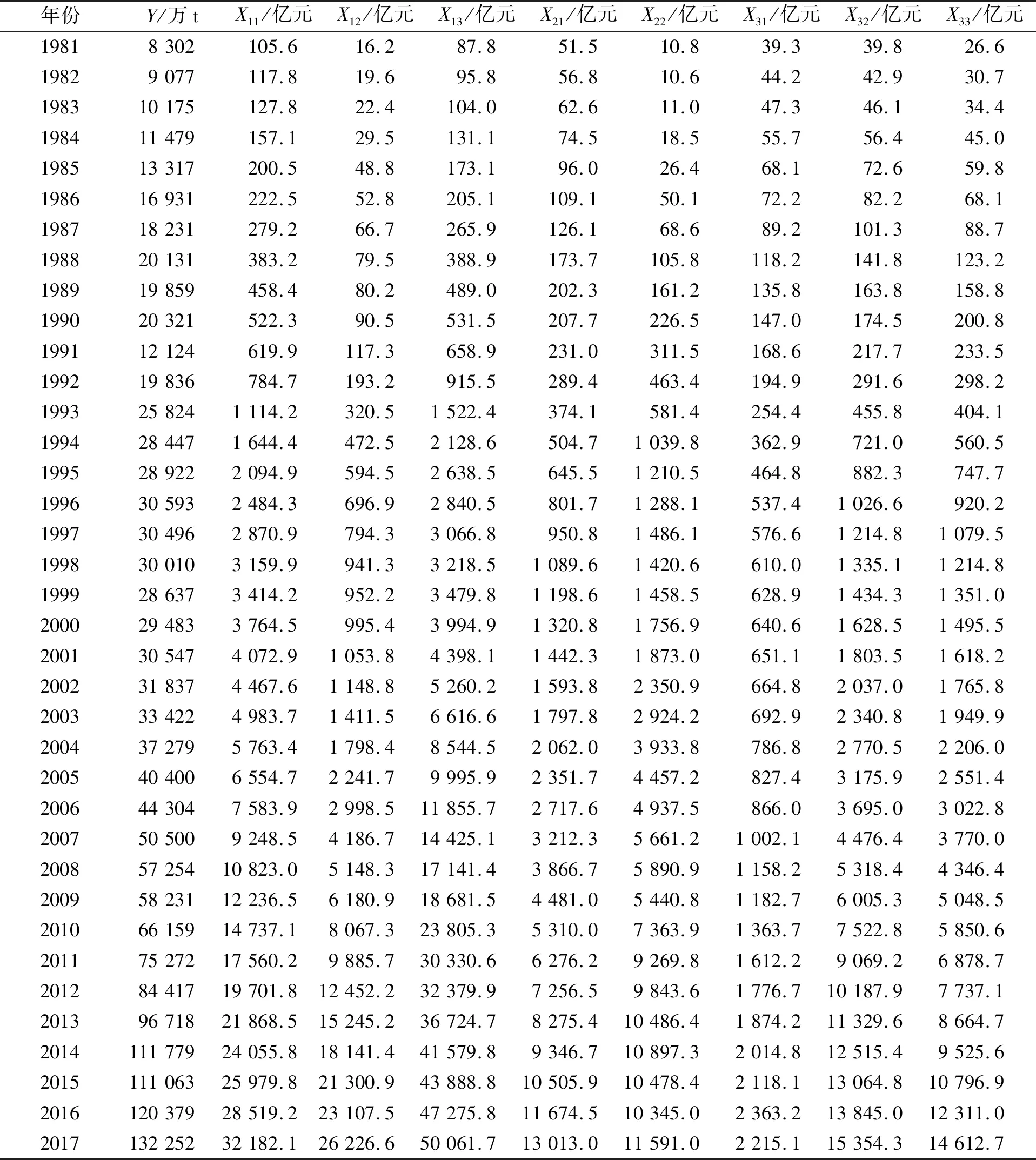
表3 福建省物流需求预测原始数据
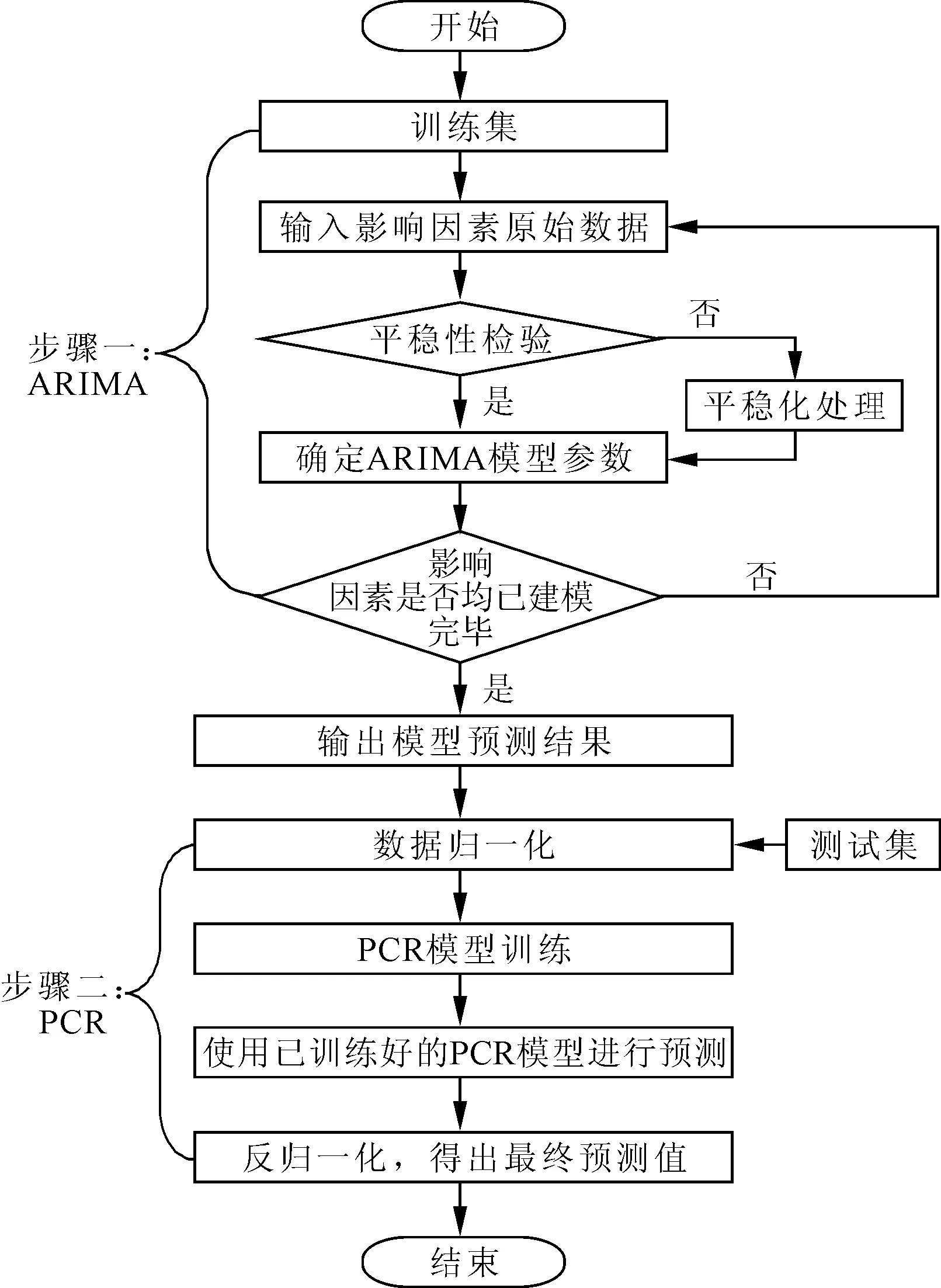
图2 基于ARIMA-PCR模型的预测流程图
2.1 基于ARIMA模型的指标预测
将表3中数据拆分为训练集(1981—2015年)和测试集(2016—2017年),训练集用于建模,测试集用于检验模型有效性。建模步骤如下:
(1)对指标X11的原始数据进行平稳性检验,若不平稳,经d阶差分,将数据转化为平稳序列。
(2)运用自回归AR(p)和移动平均MA(q)模型对平稳化后的新序列进行建模,称满足如下形式的模型为ARIMA(p,d,q)模型:
ΔdXj=φ1ΔdXj-1+φ2ΔdXj-2+…+φpΔdXj-p+
εj+θ1εj-1+θ2εj-2+…+θqεj-q
(2)
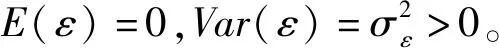
经检验确定X11的最优模型为ARIMA(1,1,1),标准化后模型的实际值、拟合值与残差序列如图3所示,可看出在经过1阶差分后,残差围绕0值上下随机波动,可认为数据干扰随机,预测值与拟合值变动趋势一致,说明所建立的模型能较好地拟合数据的真实情况。
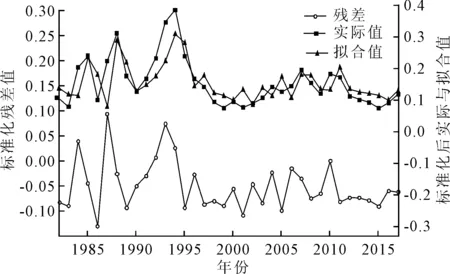
图3 ARIMA(1,1,1)模型残差、实际值与拟合值
(3)其他指标的建模步骤与上述类似,分别建立各指标的ARIMA模型及各模型2016年和2017年的预测值,如表4所示。
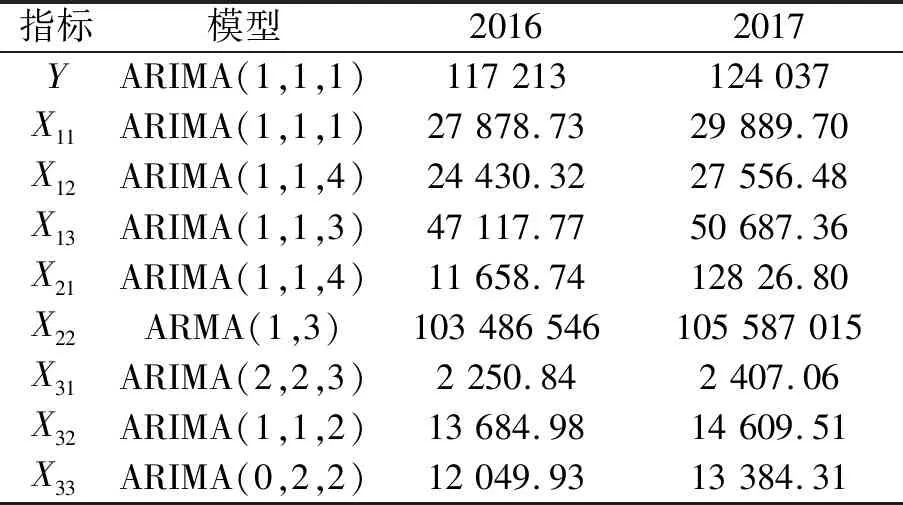
表4 指标的模型及预测值
2.2 基于PCR模型的需求量预测
(1)将各个ARIMA模型的预测数据(见表4)与训练数据集组成新的时间序列矩阵,经标准化后得到无量纲的数据矩阵X,将其作为主成分回归的输入矩阵。
(3)
其中,xij为第i年第j个指标的原始数据。
(2)计算矩阵X的相关系数矩阵R=(rij)m×n,其中rij的计算公式为:
(4)
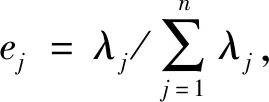
经计算可得知前两个主成分累计包含了原始数据99.634%的信息,因此提取前两个主成分,即:
Z1=0.113x1+0.111x2+0.113x3+0.113x4+
0.110x5+0.111x6+0.113x7+0.112x8
(5)
Z2=-0.062x1-1.777x2-0.079x3-0.597x4+
1.843x5+1.481x6+0.117x7-0.552x8
(6)
(4)将所提取的主成分Z1和Z2对货运量Y进行最小二乘线性回归,得到回归方程Y=33 812.882Z1+189.427Z2+43 081.297。回归方程检验结果如表5所示,可看出方差膨胀因子VIF<10,表明主成分指标不共线,所建立的回归方程有效,拟合优度R2为0.994,接近于1,回归系数落于95%置信区间内,说明模型拟合程度好。

表5 回归系数检验表
(5)将提取的两个主成分分别代入回归方程后,得到2016年和2017年福建省的货运量分别为117 213万t和124 037万t。
3 ARIMA-PCR模型的有效性及预测结果分析
为了验证所构建ARIMA-PCR模型的有效性,借鉴李赤林等[23]的研究,引用相同的数据集对各指标建立BP神经网络模型,BP神经网络的参数如表6所示,对建立的模型训练10次,加权平均得到预测值。各模型2016和2017年的预测结果与实际值对比如图4所示,由图4可知,ARIMA-PCR模型的预测值最接近实际值。

表6 BP神经网络参数
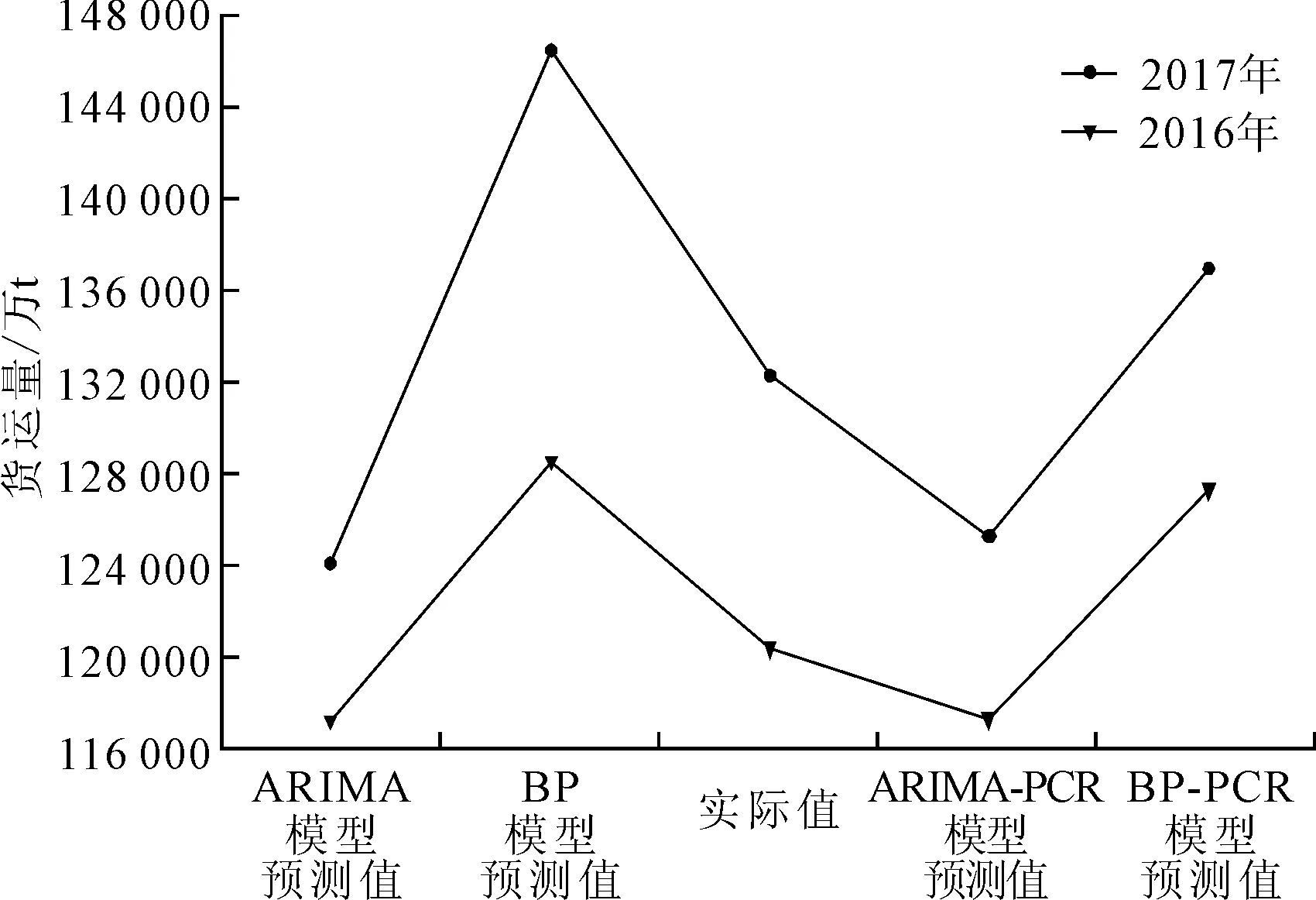
图4 各模型预测结果对比图
3.1 模型的有效性分析
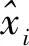
(7)
(8)
由表7可知:①BP-PCR模型、ARIMA-PCR模型的预测效果分别优于BP模型、ARIMA模型,说明选取多种影响因素对物流需求进行预测比选取货运量单一指标进行预测的结果具有更高的精度;②在预测方法上,基于主成分回归的组合模型预测效果要优于单一模型和基于多元线性回归的组合模型,这是因为主成分回归降低了指标间的多重共线性问题,减少误差,从而精度得到提升。这也是整体上ARIMA-PCR模型取得了最好预测效果的原因。

表7 各种预测方法比较
3.2 模型预测结果分析
以1981—2017年统计数据为训练集,代入已建好的ARIMA-PCR模型,预测2018—2022年福建省物流需求量,结果分别如图5和表8所示。由表8可知,2022年福建省货运量需求将达178 607万t,较2017年的132 252万t增长近35%。由图5和表8可知,未来5年,福建省物流需求量将进一步扩大。
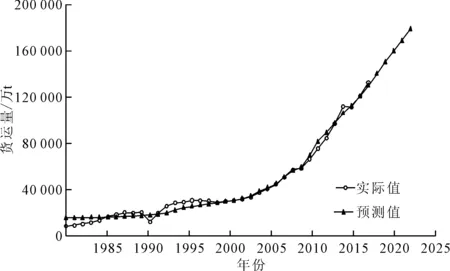
图5 ARIMA-PCR预测值与实际值对比

表8 基于ARIMA-PCR模型的货运量预测结果(2018—2022年)
4 结论
为了精准地预测福建省物流需求,为福建省物流业发展提供数据支撑和决策参考,笔者构建了ARIMA-PCR组合预测模型。首先,从多维度选取影响因素,构建物流需求预测指标体系;其次,利用ARIMA模型对各指标分别进行建模预测;最后,将预测结果进行主成分回归分析,建立货运量与所提取主成分之间的多元回归关系。结果表明,对福建省物流需求的预测,ARIMA-PCR模型相较于其他模型能取得更好的预测效果,并得到以下主要研究结论:
(1)在指标选取上,从多角度出发选取影响因素进行组合预测,其结果具有更高的精度,但是在指标选取时也要进行适当的筛选和数据降维,减少多重共线性等问题对预测结果的干扰。
(2)在预测方法上,通过对比ARIMA模型、BP神经网络模型及各组合预测模型的预测效果可知,ARIMA-PCR模型更能真实准确地反映福建省物流需求量的变化特征。
(3)根据模型预测结果可知,未来5年福建省物流需求量将保持持续增长趋势,物流业对经济的贡献度将逐年提升。基于此,福建省政府部门可以依据未来5年的物流需求量进行物流系统科学规划,加快物流节点和交通线路的投资,加强各种交通运输方式的衔接,进一步促进物流业高效率运转。物流企业要提高服务水平,转变经济发展方式,增强与制造企业等的协调联动能力。
(4)笔者侧重于从经济角度出发选取指标,在未来的研究中,可以从更多层面综合选取指标,构建指标体系进行物流需求量预测。
