考虑不确定需求的应急避难场所选址研究

李建光，赵寒青

(上海市地下空间设计研究总院有限公司，上海 200020)

近年来，大规模自然灾害在世界各地频繁发生，导致人们的生命安全受到威胁。例如，2004年印度洋海啸袭击了10多个国家，造成29.2万人死亡或失踪[1]。如何有效地实施灾害应急管理，减少经济损失，保障人身安全，降低次生灾害风险，提高人类社会应对自然灾害的应急能力，越来越受到政府部门和学者的重视。作为一种事前防灾减灾的准备措施，避难场所布局规划已经成为政府部门缓解灾害影响与提高应急救援能力的迫切需求和必然选择。

目前，国内外学者对应急避难场所选址问题进行了大量研究[2-5]。如陈志芬等[6]分析了应急避难场所层次选址的决定因素和基本目标, 并结合应急避难场所的不同选址类型, 分别以避难效果和成本为目标, 建立了包含临时、短期、中长期三级层次的应急避难场所选址模型。LI 等[7]基于时变避难需求评估，分别以最小化避难场所建设成本与受害者总疏散距离为目标，构建了一个层级应急避难场所选址模型与一个居民点分配模型。然而，避难需求的不确定性对灾害准备阶段应急避难场所布局规划提出了挑战。一些研究已经强调了应急避难场所选址问题中的不确定因素[8-10]。KINAY等[11]考虑被选避难所的利用率与能力限制，发展了一个机会约束优化模型来捕获避难需求的不确定以及优化避难节点选址。BAYRAM等[12]考虑了疏散需求的不确定性以及道路网络与避难场所的扰动，以最小化期望总疏散时间为目标，建立了一个基于场景的两阶段随机规划疏散模型，以优化避难场所选址、分派疏散者到最近的避难场所以及选择最短疏散路径。HU等[13]考虑了潮汐人群与伤员分诊，以最小化设施建设成本与最小化最坏情形疏散距离为目标，构建了一个双目标鲁棒优化模型来确定避难场所与医疗中心选址、避难场所能力、居民点对避难场所与医疗中心分配、避难场所对医疗中心分配以及相应疏散流与伤员流的大小。针对具有不确定性的疏散需求问题，以上研究或者基于期望情形运用随机规划方法[14]来优化避难场所选址，或者基于最坏情形运用鲁棒优化方法[15]来确定避难场所选址。然而，基于期望情形获得的解缺乏鲁棒性，而基于最坏情形获得的解过于保守。因此，在进行应急避难场所布局规划时，决策者需要折中考虑不确定需求的期望情形与最坏情形。

为了降低避难场所布局结果的保守性与提高布局结果的鲁棒性，笔者通过离散场景表征避难需求的不确定性，同时考虑决策者对于优化期望情形与最坏情形的偏好，以避难场所建设成本与加权的期望情形、最坏情形运输成本之和最小为目标，构建了一个鲁棒随机规划模型来确定避难场所选址以及居民点疏散者对避难场所的分配。最后，通过灾害场景设计与数值实验，分析了决策者的期望情形权重与最坏情形权重对避难场所布局的影响。

1 问题与模型

应急避难场所布局规划研究需要确定避难场所的选址以及居民点疏散者对避难场所的分配。为了有效、有序地管理疏散和运输，将一个居民点的疏散者视为一个整体，仅且被分配到一个避难场所，并非分配到两个或多个不同的避难场所。同时，为了有效减少整个疏散与运输过程的混乱与无序，尽可能避免疏散者混淆目的地避难场所，居民点对避难场所的分配考虑作为独立于场景的决策变量。此外，假定疏散者完全遵循管理者制定的疏散计划。

1.1 符号定义

(1)集合。定义I为居民点i的集合，∀i∈I；K为候选避难场所k的集合，∀k∈K；S为灾害场景s的集合，表征灾害发生强度与造成的破坏程度，∀s∈S。如针对地震灾害，其中s表征地震发生的等级与造成的破坏程度。

(2)参数。fk为避难场所k的建设成本；Γk为避难场所k的避难能力；ci,k为居民点i与避难场所k之间运输单位人流的成本；wi,s为场景s下居民点i需求避难的人数；ps为场景s发生的概率；θ为决策者偏好于优化期望情形的权重；1-θ为决策者偏好于优化最坏情形的权重。

(3)决策变量。zk为0-1变量，取值为1表示避难场所k被建立，否则为0；xi,k为0-1变量，取值为1表示居民点i的疏散者分配给避难场所k，否则为0。

1.2 模型构建

基于决策者优化期望情形与最坏情形的权重，建立鲁棒随机规划模型(M1)：

(1)

s.t.

(2)

xi,k≤zk,∀i,k

(3)

(4)

zk,xi,k∈{0,1},∀i,k

(5)

其中，式(1)为目标函数，表示最小化总成本，总成本由避难场所建设成本、加权的期望情形与最坏情形运输成本构成；约束式(2)是保证居民点i分配到一个避难场所；约束式(3)是确保每一个居民点仅且分配到一个被建立的避难场所；式(4)为避难能力约束，确保加权的期望情形与最坏情形避难需求小于等于避难场所k的能力；式(5)为0-1变量约束。

针对非线性目标函数式(1)与约束式(4)，引入两个辅助决策变量R与Uk分别线性化目标函数式(1)与约束式(4)。此时，模型(M1)可以转换为模型(M2)：

(1-θ)R

(6)

s.t.

(7)

xi,k≤zk,∀i,k

(8)

(9)

(10)

(11)

R,Uk≥0,∀k

(12)

zk,xi,k∈{0,1},∀i,k

(13)

2 数值实验

2.1 参数设定

居民点与候选避难场所的地理分布与数据信息如图1所示，居民点与候选避难场所分布在一个20×20 km2的二维平面，其中圆圈与正方形分别代表居民点与候选避难场所；不同大小的圆圈代表居民点人口(popi)的相对范围大小；不同大小的正方形代表避难场所能力的相对范围大小；各居民点的人口与避难场所的能力随机取自各自对应的区间范围。居民点i与候选避难场所k之间的距离(di,k)通过欧式距离表示。设定fk=50Γk，∀k；ci,k=5di,k，∀i,k。考虑6种灾害场景，针对s=1，设定wi,1=αi，1×popi，∀i,即场景1下居民点i的疏散人数等于该场景下的疏散比例αi，1乘以该居民点人口数量，场景1下的疏散比例αi，1～U[0.10,0.25]。类似地，基于疏散比例和居民点人口数量，其他场景下居民点疏散人数可以确定为：针对s=2，设定wi,2=αi，2×popi，∀i，αi，2～U[0.25,0.40]；针对s=3，设定wi,3=αi，3×popi，∀i，αi，3～U[0.40,0.55]；针对s=4，设定wi,4=αi，4×popi，∀i，αi，4～U[0.55,0.70]；针对s=5，设定wi,5=αi，5×popi，∀i，αi，5～U[0.70,0.85]；针对s=6，设定wi,6=αi，6×popi，∀i，αi，6～U[0.85,1.00]。此外，场景1至场景6的概率分别取为0.10、0.20、0.35、0.20、0.10与0.05；决策者基于自己的偏好在区间[0,1]内确定θ值。

在Matlab环境中编码所构建的模型M2，并调用IBM ILOG CPLEX 12.6软件求解，求解采用的电脑配置为Intel Core i5 2.67 GHz CPU与4 GB RAM。

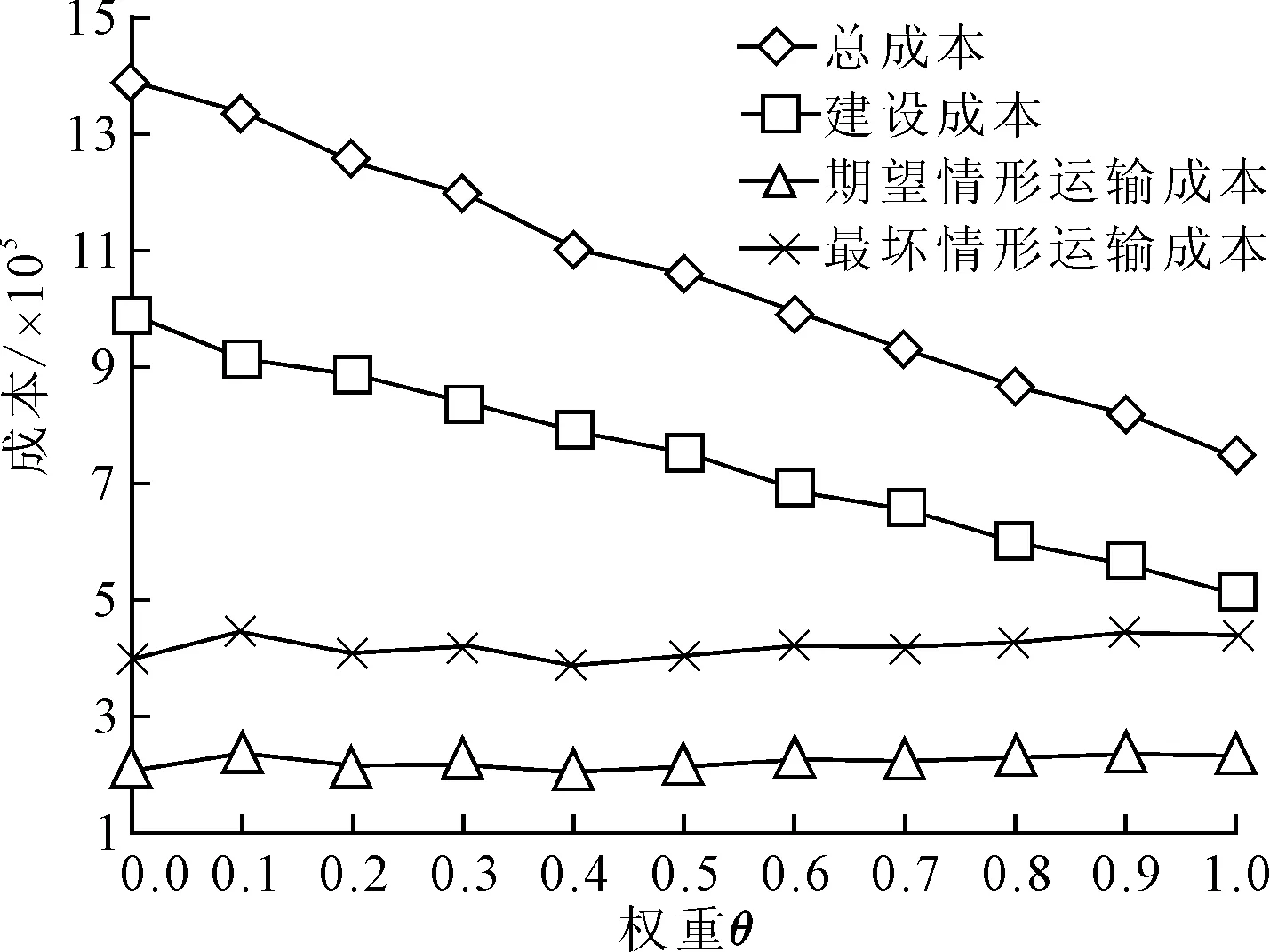
图3 不同权重θ值对成本的影响

2.2 结果分析

通过设定θ∈{0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}，分析不同θ值对避难场所选址和成本的影响。不同权重θ值对避难场所数量与成本的影响结果分别如图2和图3所示。由图2可知，随着θ值的增加，建立的避难场所数量总体上趋向于减少。虽然有不同θ值对应的避难场所数量不变、甚至随着θ值的增加避难场所数量出现反弹的情况，但结合图3可知，不同θ值产生不同的建设成本，并且随着θ值的增加避难场所建设成本逐渐下降。如当θ值从0.2变动到0.4时，尽管避难场所数量保持不变，但建设成本从8.85×105减少到7.85×105，下降幅度为11.3%；当θ值从0.9增加到1.0时，尽管避难场所数量从5增加到6，但建设成本从5.6×105减少到5.1×105,下降幅度为8.9%。随着θ值的增加，总成本逐渐减少。当θ值从0.0增加到1.0时，总成本从1.382×106减少到7.422×105，下降幅度达46.3%。这主要是因为随着θ值的增加，避难场所建设成本与加权后的最坏情形运输成本逐渐减少。同时，随着θ值的变动，期望情形与最坏情形下的运输成本基本保持在小范围内变动；最坏情形运输成本一直大于期望情形运输成本。总之，上述结果表明如果决策者偏好基于最坏情形来优化避难场所选址，则需要建立更多的避难场所，产生更高的建设成本与总成本；反之，如果决策者偏好基于期望情形来优化避难场所选址，则需要建立更少的避难场所，产生更低的建设成本与总成本。这主要是因为最坏情形下获取的解需要适用所有场景，需求对所有场景具有鲁棒性，而解的鲁棒性的获取需要通过建立更多的避难场所来实现，以使建立的避难场所能够满足不同场景下的避难需求。

同时，θ值的变化对避难场所选址及居民点对避难场所的分配产生很大影响，不同权重θ值下避难场所选址结果如表1所示，θ值分别为0.0、0.5、1.0时避难场所选址与居民点对避难场所的分配关系分别如图4～图6所示。

表1 不同权重θ值下避难场所选址结果

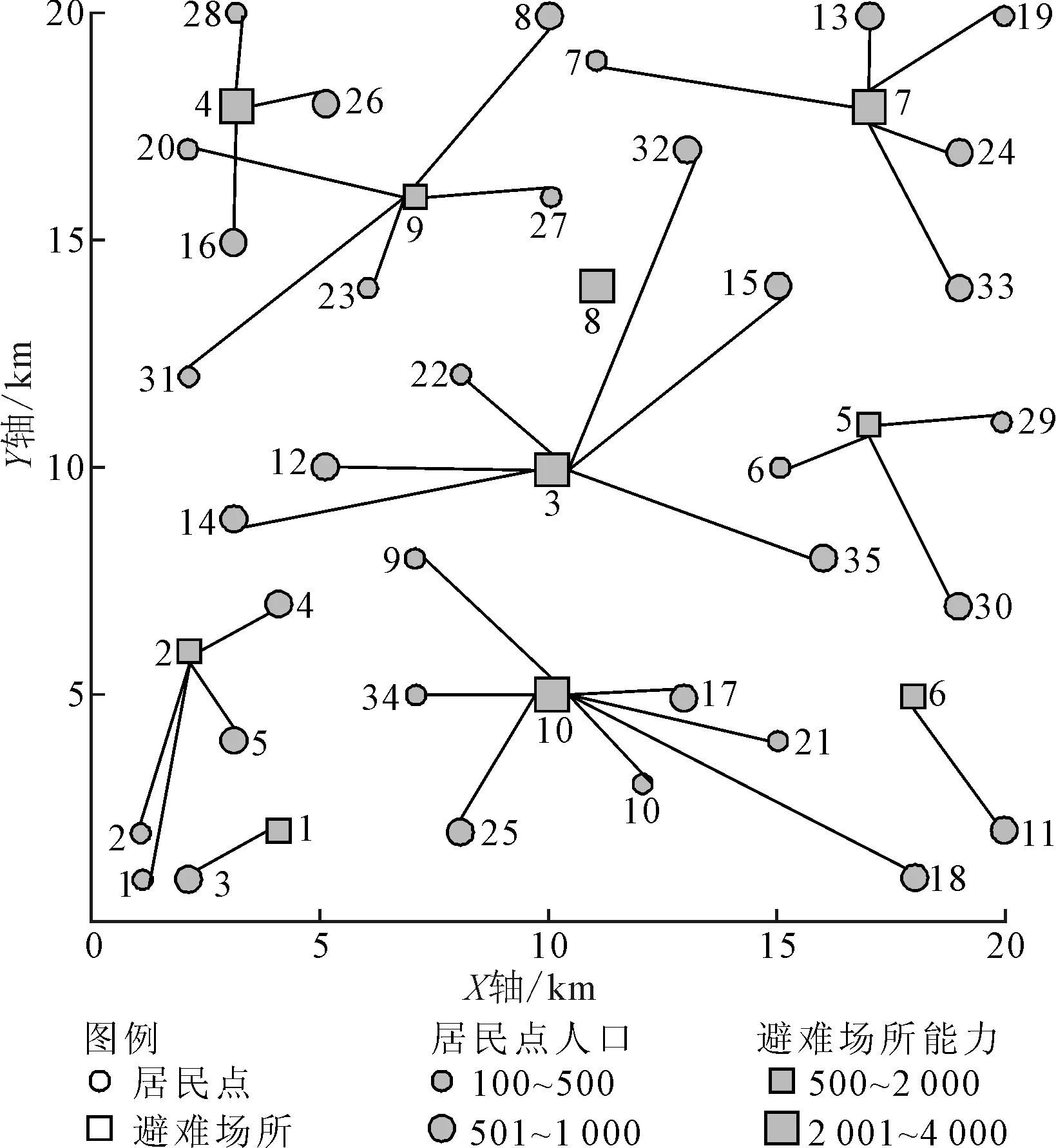
图4 θ=0.0时避难场所选址与居民点对避难场所分配关系

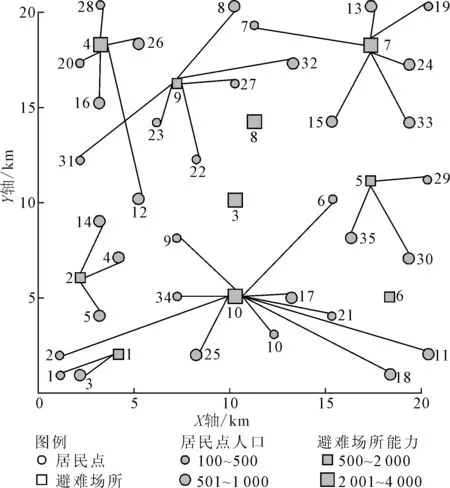
图5 θ=0.5时避难场所选址与居民点对避难场所分配关系

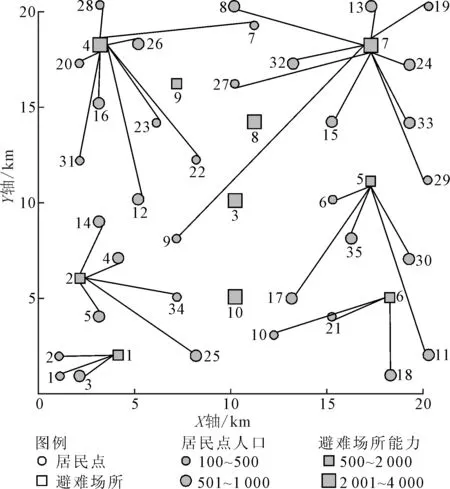
图6 θ=1.0时避难场所选址与居民点对避难场所分配关系

由上述结果可以看出，不同θ值下的避难场所选址与居民点对避难场所的分配存在明显差异。当θ值为0.0时，候选节点3与6均被选为避难场所；当θ值为0.5时，候选节点3与6未被选为避难场所。类似地，当θ值为0.5时，候选节点9与10均被选为避难场所；当θ值为1.0时，候选节点9与10未被选为避难场所，但增加节点6为避难场所。即使避难场所数量相同，但随着θ值的变化避难场所位置也存在差异。如当θ值为0.7时，候选节点1、2、4、5、7与10被选为避难场所；当θ值为0.8时，候选节点1、2、4、6、7与10被选为避难场所。并且由于避难场所位置的改变，相应居民点对避难场所的分配关系也发生了变化。此外，由于候选避难场所的地理位置与建设成本的相对大小，候选避难场所2、4与7在不同θ值下一直被选为避难场所，对不同的θ值具有鲁棒性。

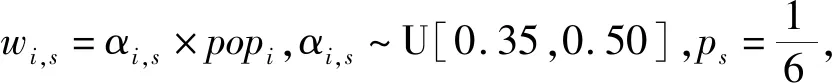
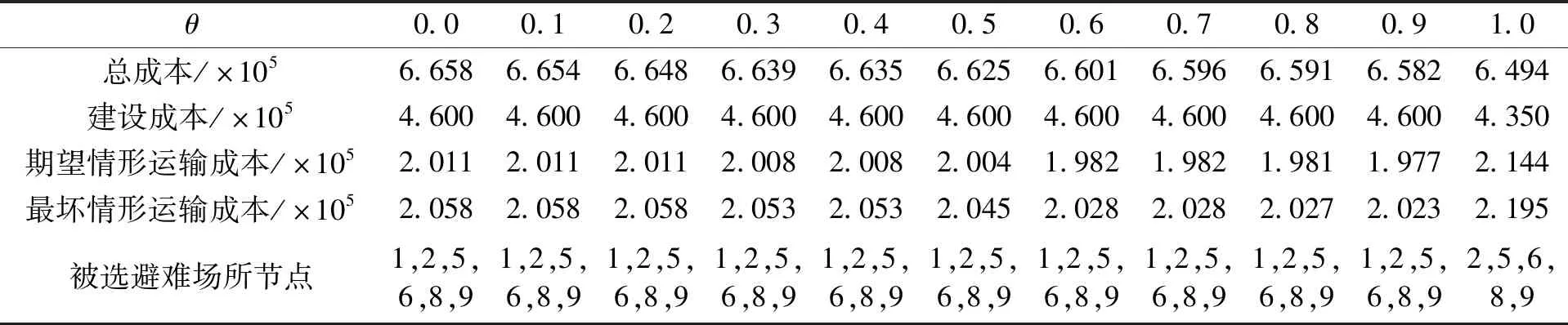
表2 相似场景下不同θ值时求解模型[M2]的结果

3 结论

笔者主要研究了具有不确定避难需求的避难场所选址问题，通过场景表征居民点避难需求的不确定性，考虑决策者对优化期望情形与最坏情形的偏好，运用随机优化与鲁棒优化方法构建了一个鲁棒随机规划模型，以确定避难场所选址、居民点对避难场所的分配。结果表明：如果决策者偏好基于最坏情形来优化避难场所选址，则需要建立更多的避难场所，产生更高的建设成本与总成本；反之，如果决策者偏好基于期望情形来优化避难场所选址，则需要建立更少的避难场所，产生更低的建设成本与总成本。如果灾害场景类似，则期望情形相似于最坏情形，基于优化期望情形获得的避难场所选址与居民点对避难场所的分配接近基于优化最坏情形获得的结果。

笔者假定居民点疏散需求的分配为独立于场景的决策变量。如果疏散者能够获得及时的协助或指示，则未来研究可以考虑将居民点的疏散需求分配视为取决于场景的决策变量。同时，笔者仅研究了避难场所选址-分配问题，未来应该扩展研究不确定需求下避难场所选址-路径问题。