复杂抽样调查设计二值资料一水平多重Logistic回归分析

王 娇，李长平，2*，胡良平

（1. 天津医科大学公共卫生学院卫生统计学教研室，天津 300070；2. 世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3. 军事科学院研究生院，北京 100850

*通信作者：李长平，E-mail：1067181059@qq.com）

抽样调查由于省时省力且灵活性高，在流行病学调查中应用广泛。最基础的抽样方法包括简单随机抽样、系统抽样、整群抽样和分层抽样。但是，在多中心及大规模的调查中，通过单一的抽样方法获取的样本往往代表性不好，因此常将多种抽样方法组合在一起使用，即复杂抽样［1］。复杂抽样通常具有分层、整群、不等概率或多阶段实施等特点，其产生的样本称为复杂样本。由于复杂抽样各阶段所采取的抽样方法不一定相同，因此，抽样误差的估计会变得极为复杂，若计算时不考虑抽样设计，可能会造成错误的统计推断结果，从而得到错误的结论。本文通过不同的分析策略实现了对复杂抽样调查设计二值资料一水平多重logistic 回归分析，并探讨了各种分析策略之间的差异。

1 基本概念

1.1 常见复杂抽样调查设计种类

1.1.1 分层随机抽样调查设计

分层随机抽样是按一定标准先将总体各单位分层，然后根据各层样本量在总体样本量中的占比，确定从各层中抽取样本的数量，最后按照随机原则从各层中抽取样本。分层随机抽样适用于总体样本量较大、内部变异较大的调查对象。分层因素的选取需要把握好专业知识。

1.1.2 整群随机抽样调查设计

整群随机抽样是将总体按一定标准划分成群或集体，以群或集体为单位按随机原则从总体中抽取若干群或集体作为总体的样本，并对抽中的各群或集体中每一个单位都进行实际调查。

1.1.3 多阶段随机抽样调查设计

多阶段随机抽样是先将调查总体各单位按一定标准分为若干集群，作为一级抽样单元，按照随机原则，先在一级抽样单元中抽出若干单元作为一级单元样本，再在第一级单元样本中抽出二级单元样本，以此类推，抽取第三、第四级单元样本。调查工作至第二级单元样本者，为两阶段随机抽样；至第三级单元、第四级单元样本者，分别为三阶段和四阶段随机抽样。多阶段随机抽样适用于总体的范围大、单元多、情况复杂的调查研究场合。

1.2 抽样调查设计中权重的种类

1.2.1 概述

权重是一个相对的概念，用来描述某一指标或个体在整体评价中的相对重要程度。研究表明，复杂抽样资料的分析应同时考虑观测权重与抽样权重，并提出了综合权重的概念，纳入综合权重的结果更加灵敏、准确、稳健［2］。

1.2.2 观测权重

观测权重是基于权重系数的思想，在分析中引入一个度量每个个体或观测对总体的重要程度的指标，表示在其他个体不变的情况下，该个体的变化对结果的影响程度。由于抽样研究中每个个体的重要程度有差异，在确定每个个体的观测权重时应根据实际情况做出合理规定。常用的定义观测权重的方法有经验权重法、贡献权重法和试验次数权重法等。

1.2.3 抽样权重

抽样权重是反映所抽取的样本中各个观测在总体中的重要程度或样本中各个观测代表总体中个体的数目的指标。抽样权重与抽样方法有关，分为基础抽样权重、调整抽样权重与总抽样权重［3］。在多阶段复杂抽样中，最终的抽样权重为多个抽样概率倒数的乘积［4］。

1.2.4 综合权重

评价一个调查研究所得到的样本观测的重要程度需要从不同方面进行综合考虑，因此，在同时考虑观测权重和抽样权重的情况下，定义了综合权重：综合权重=观测权重×抽样权重。

2 多重logistic回归模型的构建与求解

复杂抽样数据多重logistic 回归模型的构建、求解的思路和方法与“非配对设计二值资料一水平多重logistic 回归分析”基本相同，参见文献［5］，其区别仅在于多考虑了“权重”，其参数估计求解于下面的对数似然方程：

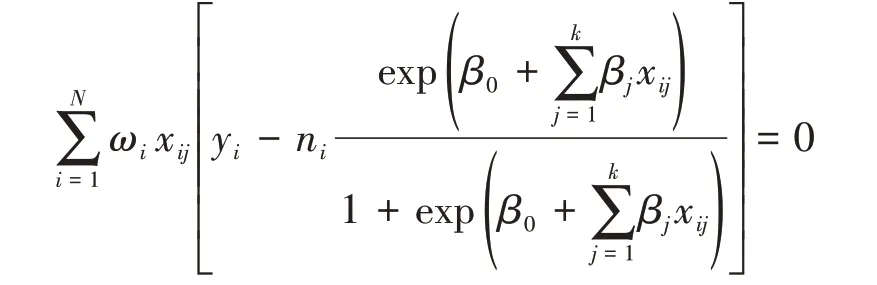
这种结合了权重的似然估计称为加权极大似然估计。对对数似然方程关于参数求偏导数，并借助非线性迭代法求解出参数的估计值。

3 基于SAS的实例分析

3.1 问题与数据

本研究中使用的数据是中国教育追踪调查（China Education Panel Survey，CEPS）的基线数据。CEPS使用多阶段概率和规模成比例（PPS）采样方法，抽样过程分为四个阶段。调查的起点是两个年级。在第一阶段，平均教育水平和流动人口比例是分层变量，从全国范围内随机选择28个县级单位为调查点；第二和第三阶段的调查是在学校进行的。从选定的县级单位中随机抽取112 所学校的438 个班级进行调查；第四阶段对第三阶段所选择班级的全部学生进行了调查，在基线时对大约20 000名学生进行调查。本例以年级为因变量来研究两个年级（1=七年级、2=九年级）学生之间的差异，选取的自变量包括语文成绩、数学成绩、英语成绩、性别（1=男生、2=女生）、户籍类型（1=农村、2=非农村）、是否为独生子女（1=不是、2=是）、父母是否在家（1=都在家、2=一方不在家或都不在家）、是否住校（1=是、2=否）、父亲是否酗酒（0=否、1=是）、父母是否经常吵架（0=否、1=是）和父母是否关系很好（0=否、1=是）。见表1。

表1 七年级和九年级学生基线资料

3.2 分析策略

在上述实例数据中，语文成绩、数学成绩和英语成绩三个变量为定量资料，在原始数据的基础上分别产生12个派生变量（x1-x12），代码如下：

（此处输入表1 中全部数据，19487 行、15 列（含编号列））

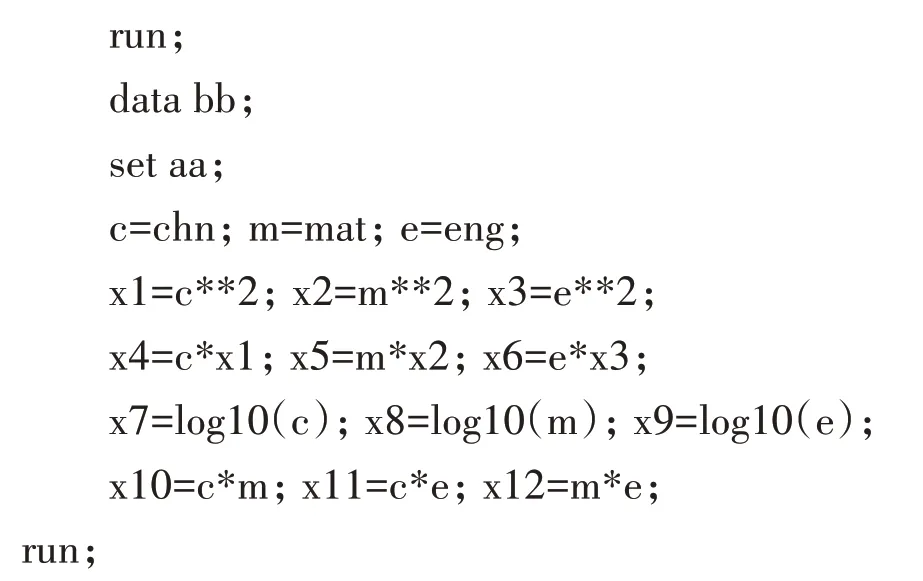
3.2.1 不考虑抽样设计和抽样权重，使用原始变量（模型1）

需要调用LOGISTIC 过程来实现单纯随机抽样资料的多重logistic回归分析。

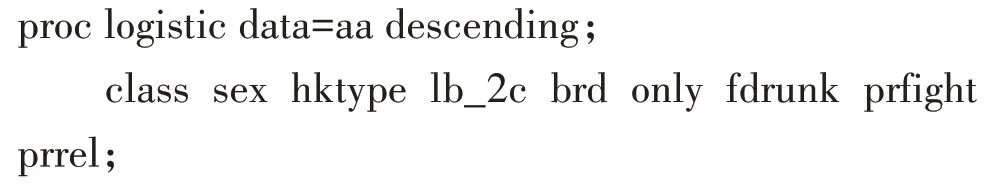
【说明】“descending”选项是要求给出“Y=2”（九年级）发生概率的计算结果，否则，给出“Y=1”（七年级）发生概率的计算结果；“class语句”定义了性别、户籍类型、父母是否在家、是否住校、是否独生、父亲是否酗酒、父母是否吵架和父母关系为解释变量中的分类变量；“model语句”中的selection=backward选项定义后退法来选择变量；sls=0.05选项定义变量的保留标准为P＜0.05；RSQ选项输出广义R2。

3.2.2 不考虑抽样设计和抽样权重，使用原始变量和派生变量（模型2）

3.2.3 考虑抽样设计但不考虑抽样权重，使用原始变量（模型3）

需要调用SURVEYLOGISTIC 过程来实现复杂抽样数据的多重logistic回归。

【说明】PROC SURVEYLOGISTIC 用于处理抽样调查数据，在分析过程中将抽样设计信息纳入分析。本例为多阶段分层抽样，一般以一级抽样单位为分层变量，因此用strata语句来定义分层变量为所在县、市、区（ctyids）。“model语句”中的ref='1'选项定义以y=1为参考进行建模。由于SURVEYLOGISTIC过程不能进行变量筛选，在初次分析后剔除了三个没有统计学意义的变量（户籍类型、父母是否吵架、父母关系），进行最终的建模。

3.2.4 考虑抽样设计但不考虑抽样权重，使用原始变量和派生变量（模型4）

代码从略。最终模型中剔除了11 个没有统计学意义的变量（x3、x4、x6、x10-x12、英语成绩、户籍类型、父亲是否酗酒、父母是否吵架、父母关系）。

3.2.5 不考虑抽样设计但考虑抽样权重，使用原

始变量（模型5）

【说明】加入了weight 语句来利用权重，本例仅考虑抽样权重来拟合多重logistic 回归模型。最终模型剔除了（户籍类型、是否独生、父母是否吵架）三个没有统计学意义的变量。

3.2.6 不考虑抽样设计但考虑抽样权重，使用原始变量和派生变量（模型6）

代码从略。最终模型中剔除了10 个没有统计学意义的变量（x3、x6、x10-x12、英语、户籍类型、是否独生、父亲是否酗酒和父母是否吵架）。

3.2.7 同时考虑抽样设计和抽样权重，使用原始变量（模型7）

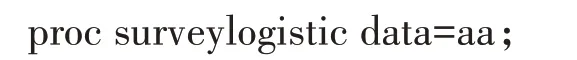
【说明】在SURVEYLOGISTIC 模型中同时加入了strata 语句和weight 语句来拟合模型。最终模型剔除了三个没有统计学意义的变量（户籍类型、是否独生、父母是否吵架）。

3.2.8 同时考虑抽样设计和抽样权重，使用原始变量和派生变量（模型8）

代码从略。最终模型剔除了10 个没有统计学意义的变量（x3、x4、x6、x10-x12、户籍类型、父亲是否酗酒、父母是否吵架、父母关系）。

3.3 不同分析策略结果比较

不同的分析策略最终纳入模型的变量不同。八个模型拟合结果见表2。

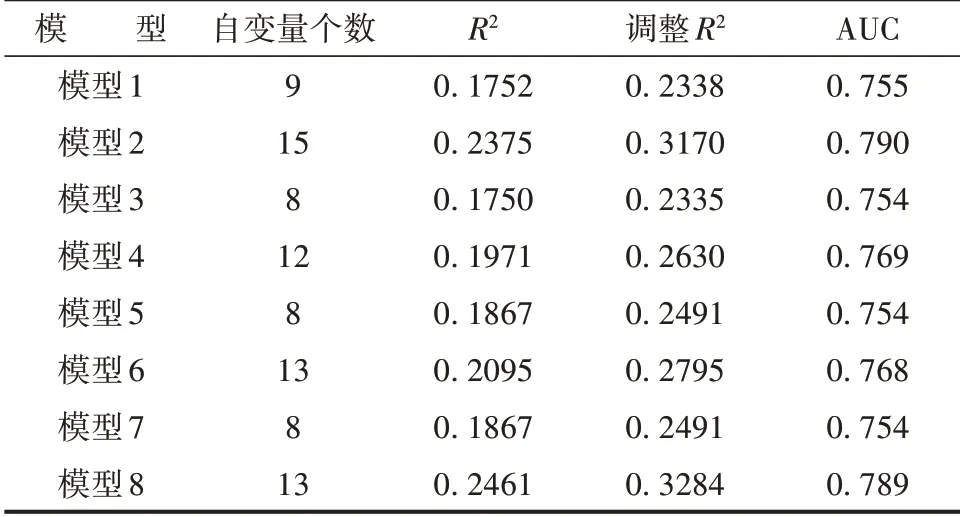
表2 各模型拟合结果比较

由表2可知，不考虑抽样设计和抽样权重时，独生子女和父母关系均有统计学意义；考虑抽样设计后，是否为独生子女这个变量有统计学意义，而父母关系这个变量无统计学意义；考虑抽样权重后，是否为独生子女这个变量无统计学意义，而父母关系有统计学意义。考虑抽样权重的模型比不考虑抽样权重的模型R2更大；同时考虑抽样设计和抽样权重的模型R2最大（R2=0.2461，调整R2=0.3284）。各模型的AUC 相差较大，而同时考虑抽样设计和抽样权重的模型AUC为0.789，在八个模型中表现较好。在纳入派生变量后，模型R2和AUC大于不考虑派生变量时模型的值。

4 讨论与小结

由于不同群体特征的可变性，研究人员在样本选择过程中应采用科学的抽样设计，以降低得出错误结论的风险，并根据样本调查数据的信息对群体进行推断。为了对调查资料做出统计上的有效推断，必须在数据分析中考虑抽样设计。在当前流行病学调查中，logistic回归分析因其能处理结局变量为离散型变量，尤其是二分类变量而广泛使用。但是，在普通的logistic回归分析中没有考虑抽样设计和抽样权重，而是假设所有的样本均来自单纯随机抽样，这可能造成信息损失和结果分析的偏差。

在实际调查中，由于抽样设计和抽样总体的变动，每一个体对结果影响的权重是不同的［2］，应分别加以考虑。本研究给出的实例采用多阶段的概率与规模成比例抽样，抽样权重为31.506～5 376.874，如果忽略了权重，分析结果可能会与实际结果之间有差异。而采用最大似然法拟合离散响应调查数据的SURVEYLOGISTIC 回归模型，其方差估计采用泰勒级数（线性化）方法或重采样方法，考虑了复杂抽样设计，包括分层、整群和权重不等的设计［6］。

由本研究结果可知，在考虑了抽样权重后，变量之间的差异会与单纯随机抽样和仅考虑了抽样设计有所不同。忽略抽样权重时，模型参数的标准误降低，OR 值的置信区间变窄，但真实数据的分布可能没有这么精确［7］。由于原始数据中仅提供了“抽样权重”而未提供“观测权重”，故本研究无法对使用不同权重后对回归分析结果的影响加以评价。

但本研究所采用的“调查数据”中的“二值因变量（年级）”不是十分合格的“因变量”，它更适合充当“原因变量”。因为通常的“二值因变量”是每个受试对象在收集资料时可能会出现两种结局之一，并且每种结局会以一定的概率出现［例如每位患者经过治疗后，可能会以概率P出现“存活”，而以概率（1-P）出现“死亡”；而在本例中，每个学生要么属于七年级、要么属于九年级，不可能以概率P属于七年级，而以概率（1-P）属于九年级］。由于没有找到合适的复杂抽样调查数据，仅借用本例来演示如何更全面地对复杂抽样调查资料进行二值资料一水平多重logistic回归分析。