基于模态展开法的水下航行器辐射噪声远场预测方法研究

周思同， 帅长庚， 杨家轩

( 1.海军工程大学 振动噪声研究所，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033；3.中国人民解放军92337部队，辽宁 大连 116023；4.海军潜艇学院，山东 青岛 266199)

声辐射快速预测对水下航行器的声场监测及减振降噪有重要的意义。目前，针对水下航行器的辐射噪声预报主要在水下试验场进行[1]，或在航行器结构表面布放大量声压或振速传感器，利用近场声全息技术(Near-field Acoustic Holography，NAH)[2]进行结构体的声场重建和预测。

基于边界元法的近场声全息技术可以对任意形状的声源进行分析，但计算量大，而且其中存在的奇异积分处理和特征波数处解的非惟一性等问题[3]。基于Helmholtz 最小二乘法的近场声全息技术是将声源分解成有限模态的正交球面波的叠加，对于非球形结构体，其计算精度也受到影响[4]。波叠加法虽然[5]具有较高的计算精度与计算效率，且不要求测量面与辐射面共型。但需要解决虚拟源优化配置的问题。基于空间Fourier变换法的近场声全息技术[6]由于声场的截断、公式的离散化处理以及Fourier变换的应用，存在“卷绕误差”、“窗效应”等算法误差，要求全息面远大于结构体表面。以空间Fourier变换法的思想为理论基础，Hald等[7-8]提出了统计最优近场声全息(Statistically Optimized Near-field Acoustical Holography, SONAH)。SONAH虽然适合用于圆柱体的声场重建，但在进行有限长圆柱辐射声场预测仿真时发现SONAH也存在局限性：①要求重建面与全息面必须很近，当重建距离超过一个波长时，在辐射圆附近汉克尔函数幅值发生突变，这种突变会产生类似数据截断的效应，导致重构信号剧烈波动，产生极大的重构误差[9-10]；②SONAH方法虽然借助全息面及重建面的柱波波谱之间线性关系求解声压叠加系数，避免使用离散空间Fourier变化造成窗效应与卷绕误差，但未对圆柱边界振动进行合理约束，声场重建的复声压信号是由全息面上的实测信号经过周期性复制延拓获得，最终造成全息孔径以外的重建信号出现周期性虚像[11]，该方法属于一种patch声全息技术。因此SONAH主要适用于结构体近场或局部重建，远场预测范围有限。

为了弥补上述方法的不足，实现水下航行器的辐射声场预测，本文提出了 “基于模态展开法的声场预测”算法。该算法将介质中有限长圆体的径向振动用轴向及周向模态表示，并建立各阶模态与全息面之间的传递函数矩阵，通过匹配全息面声压或振速来确定各阶模态系数。然后通过少量远场声压数据进行最小二乘意义下的参数匹配，获取最优模态阶数，最终实现辐射声场的预测。

1 理论分析

如图1所示，将长度为L，半径为a的圆柱壳两端分别简支在刚性无限长声障板上，此时圆柱壳表面的振动在其两端会产生反射，沿轴向形成驻波振动，任意形式下的振速分布均可展开为周向及轴向的振动模态叠加，同时也声场也可按该模态展开[12-13]。壳体表面振动引起其表面介质振动而产生声场，声场中声压满足波动方程

(1)

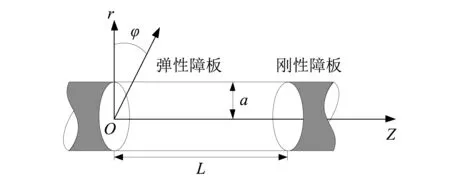
图1 有限长弹性圆柱壳体Fig.1 Finite length cylindrical shell and

考虑到壳体表面的边界条件，圆柱壳表面的径向振动与介质的质点振动相等，壳体振动沿轴向方向具有驻波形式，通过周向及轴向模态展开

(2)

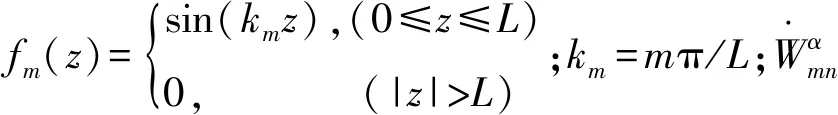
(3)

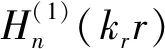
(4)

根据常用函数积分表，式(4)可化简为

(5)

将式(5)代入式(3)得

(6)

式中：kz max为轴向截止波数；N为周向最大模态阶数；M为轴向最大模态阶数。定义模态数κ=(α,m,n)在柱坐标系R=(r,φ,z)处的声压基函数

(7)

因此式(6)中柱坐标系R=(r,φ,z)处的声压可写成

(8)

将式(8)转换成矩阵形式

P=ApW

(9)

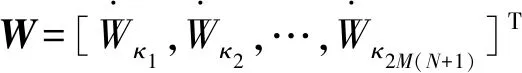
(10)

由式(9)可知，通过全息面复声压向量P及Ap求逆，可得模态系数向量W，再通过式(6)可计算出任意空间位置的声压值。Ap求逆过程需要进行正则化处理来解决不适定问题，如采用Tikhonov方法+L曲线法。根据Euler方程，由式(6)可得质点径向振速为

(11)

同理，定义模态数κ=(α,m,n)在柱坐标系R=(r,φ,z)处的振速基函数

(12)

式(11)可改写成矩阵形式

V=AvW/(iρω)

(13)

式中：向量V=[v(R1),v(R2),…,v(RX)]T为全息面上的X个复振速构成的振速向量，振速传递函数矩阵为

(14)

参数M,N,kzmax的选取是影响声场预测精度的重要因素，根据奈奎斯特空间采样定理，若网格间距为d，则全息面上各方向的波数分量<π/d。因此在圆柱全息面上，波数域轴向截止波数须满足|kzmax|<π/dz，dz为全息面网格的轴向间隔；周向最大模态阶数N<π/dφ，dφ为全息面网格的周向间隔。在此基础之上，可通过采集若干远场线阵声压数据，利用最小二乘意义下的最优参数匹配方法获取最优参数，原理如下

(15)

式中：Pr为远场线阵的测量声压；Py为模态展开法的预测声压；I为二者的归一化均方误差(Normalized Mean Square Error，NMSE)，C为最低精度需求，远场线阵声压节点总数为K，y=(M,N,kz max)为配置的参数。

2 数值仿真

利用全息柱面的声压、振速数据对点声源、圆柱模型及船舶模型进行声场预测仿真。图2为全息面与预测面示意图，(rH,φH,zH)，(rS,φS,zS)分别为全息柱面与预测柱面的坐标。当φS=π时，可进行结构体在XOZ平面(水平方向)的声场预测。

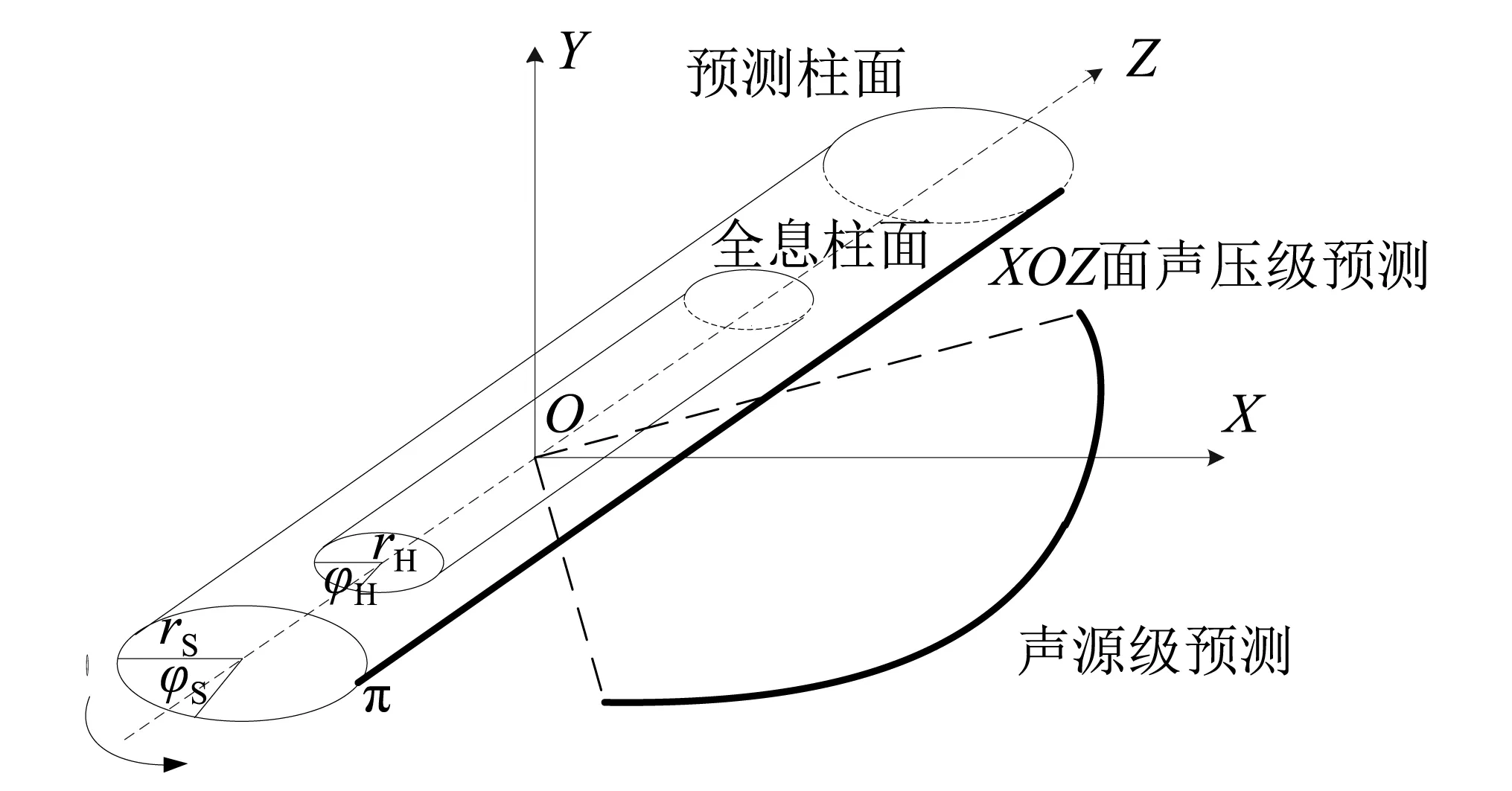
图2 全息面与重建面空间关系Fig.2 Holographic surface and reconstruction surface

2.1 点声源的辐射声场预测

通过圆柱SONAH及本文所提出的模态展开方法进行脉动球组合声场的预测仿真。脉动球质点声压为

(16)

仿真参数如下：在柱坐标系(r,φ,z)=(0,0,±20 m)的两个相同脉动球，脉动球振动频率f=200 Hz，脉动半径a=0.05 m，振速v0=0.01 m/s，传播介质为水。全息柱面为rH=4 m，-30 m≤zH≤30 m，0<φH<2π；全息面网格轴向间隔dz=2 m，周向间隔dφ=π/18，通过远场声压数据进行参数匹配，获取模态展开法参数如下：轴向最大模态阶数M=14，周向最大模态阶数N=10，轴向截止波数kz max=1.5。而SONAH参数可根据文献[15]设置，其预测面声压表达式为

(17)

式中：L为全息柱面长度；轴向最大波数kz max=π/dz；离散波数间隔dkz=π/M1dz；N1=π/dφ；M1=L/2dz。

图3为XOZ平面rs=5 m，φs=π，-150 m≤zS≤150 m处的预测声压级。由图3可看出利用圆柱SONAH进行声场预测时，在全息孔径以内范围(-30 m≤zS≤30 m)预测效果较好，而在全息孔径以外范围出现周期性的“虚像”。而利用模态展开法在全息孔径以外可获得很好的预测结果。

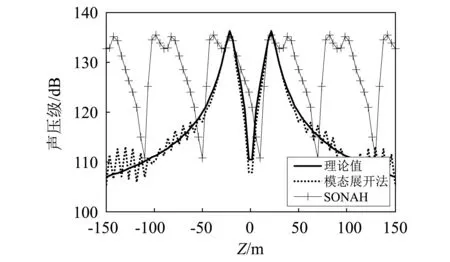
图3 XOZ平面的预测声压级Fig.3 Predicted sound pressure level of XOZ plane

对比不同模态阶数下模态展开法的声压预测值与理论值的NMSE，如表1所示。声源分布及计算参数与脉动球仿真一致。表1中第一列为远场预测柱面rS=300 m，0<φS<2π，-150 m≤zS≤150 m的声压NMSE；表中第二列为近场预测柱面rS=rH=4 m，0<φS<2π，-150 m≤zS≤150 m，既全息面处的声压NMSE。可看出不同频率下存在一个最优阶数(M,N)，高于或低于最优阶数均会导致远场预测误差增加甚至失效，且不能同时保证在最优阶数(M,N)下近场全息面处的NMSE与远场预测面的NMSE均保持较小值，这是由于当全息面与重建面距离较远时，位于辐射圆之内的传播波数成分衰减较慢，位于辐射圆之外的倏逝波数成分衰减较快，以至在辐射圆附近汉克尔函数幅值发生突变，这种突变会产生类似数据截断的效应，导致重构信号剧烈波动，产生较大的重构误差。因此仅依靠近场全息面的数据无法准确进行远场辐射噪声预测。而通过采集若干远场声压数据进行参数匹配确定最优阶数，可获取较理想的远场预测结果。

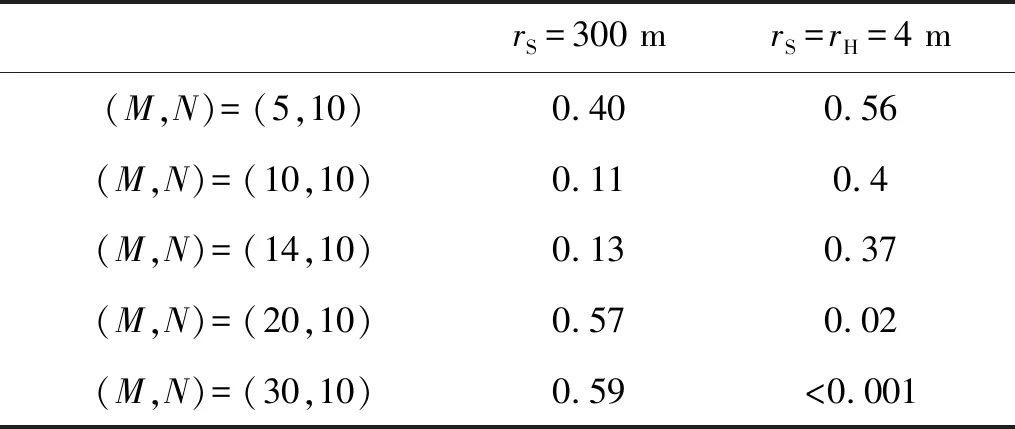
表1 不同模态阶数下的归一化均方误差

2.2 圆柱模型的辐射声场预测

通过virtual.lab有限元软件进行圆柱体声振耦合仿真，分析模态展开法对单频激励下圆柱体的声场预测性能。首先通过有限元自动匹配边界(Automatic Matched Layer，AML)方法建立了圆柱体有限元模型，模型参数如下：传播介质为水，圆柱体模型长60 m，半径3 m，厚度0.25 m，网格尺寸0.25 m×0.25 m，可计算的最高频率为1 000 Hz，材料密度7 850 kg/m3，杨氏模量2.1×1011N/m2，泊松比为0.3。在其表面添加200 Hz的单频激励，其坐标为(γ,φ,z)=(3 m,1.25 π,5 m)，对单频激励下的圆柱壳体进行声振耦合计算，可计算圆柱体表面及空间任意位置的声压及质点振速。

全息柱面为rH=3 m，0<φH<2π， -30 m≤zH≤30 m；dz=2 m，dφ=π/18。通过远场声压数据进行参数匹配，获取模态展开法参数如下：最大模态阶数M=10，N=10，轴向截止波数kz max=1.5。通过有限元计算，得到圆柱体全息柱面声压云图及XOZ平面场点声压云图，如图4、图5所示。看出圆柱体表面声压分布复杂，XOZ平面上辐射旁瓣较多。其中圆柱模型中心位于坐标原点O，轴向与Z轴同向。

图4 圆柱体全息面声压云图Fig.4 Sound pressure nephogram of cylindrical holographic surface

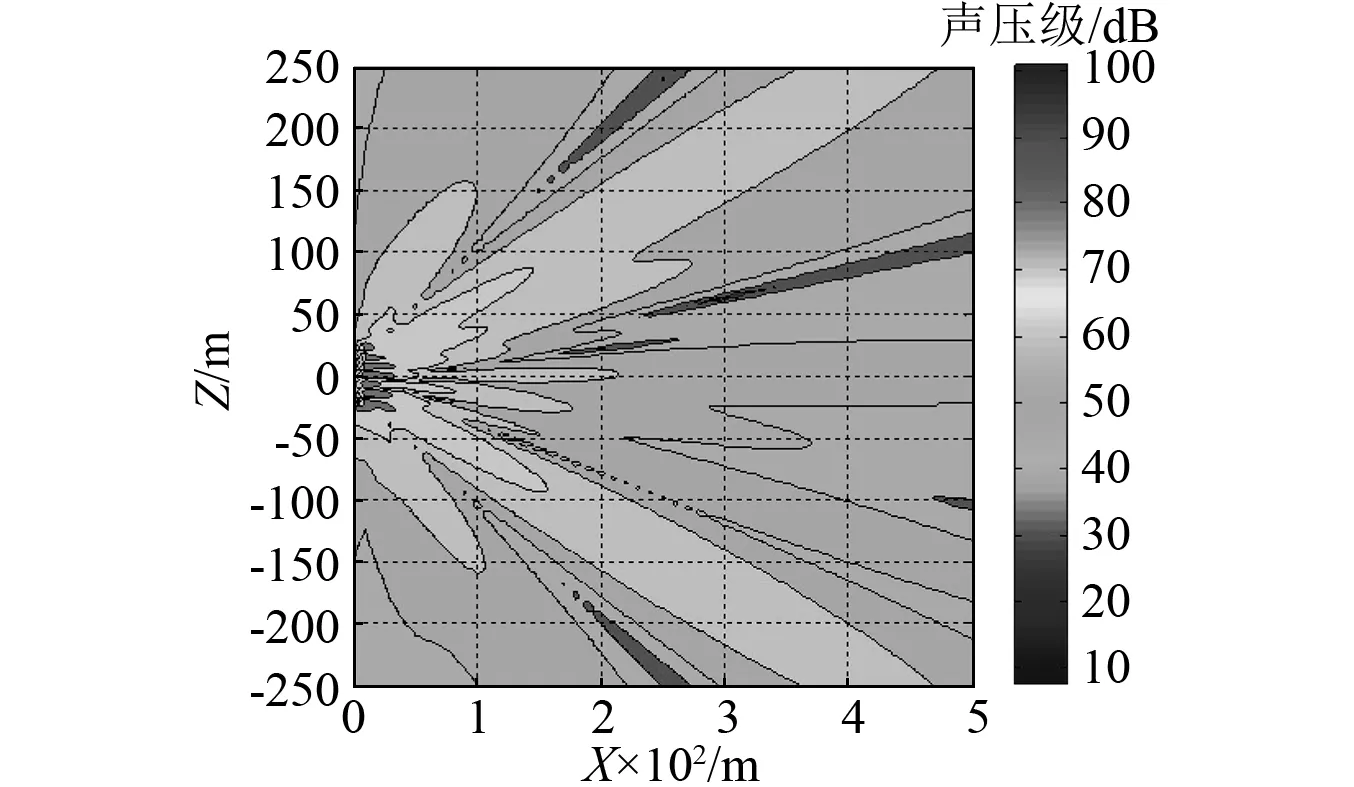
图5 XOZ平面上声压云图Fig.5 Sound pressure nephogram of XOZ plane

为了评估圆柱体远场辐射声压的预测范围及精度，在XOZ平面以坐标原点O为中心，X轴方向为0°，在半径250 m处-80°～80°范围内的弧线作为预测面，将预测声压值按照球面扩展转化，得到坐标原点1 m处的声源级，并与理论值进行比较，结果如图6所示。由图6可知，采用结构表面的声压和径向振速均能获得比较理想声压预测结果。但由于全息孔径有限，全息面轴向边缘的声源信息丢失较多，数据的不连续性较为严重，圆柱体首尾部方向声源级预测存在较大误差，沿圆柱径向-50°～50°扇形范围为有效预测区域，如图7所示。

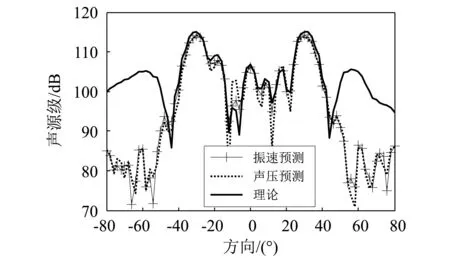
图6 XOZ平面预测声源级Fig.6 Predicted sound source level of XOZ plane

2.3 船舶模型的辐射声场预测

通过virtual.lab有限元软件进行船舶模型的声振耦合仿真，分析模态展开法对多点激励下非规格圆柱体的声场预测性能。模型参数与“2.2”节圆柱体一致，在模型中部添加两个同向200 Hz的单频激励，如图8所示。

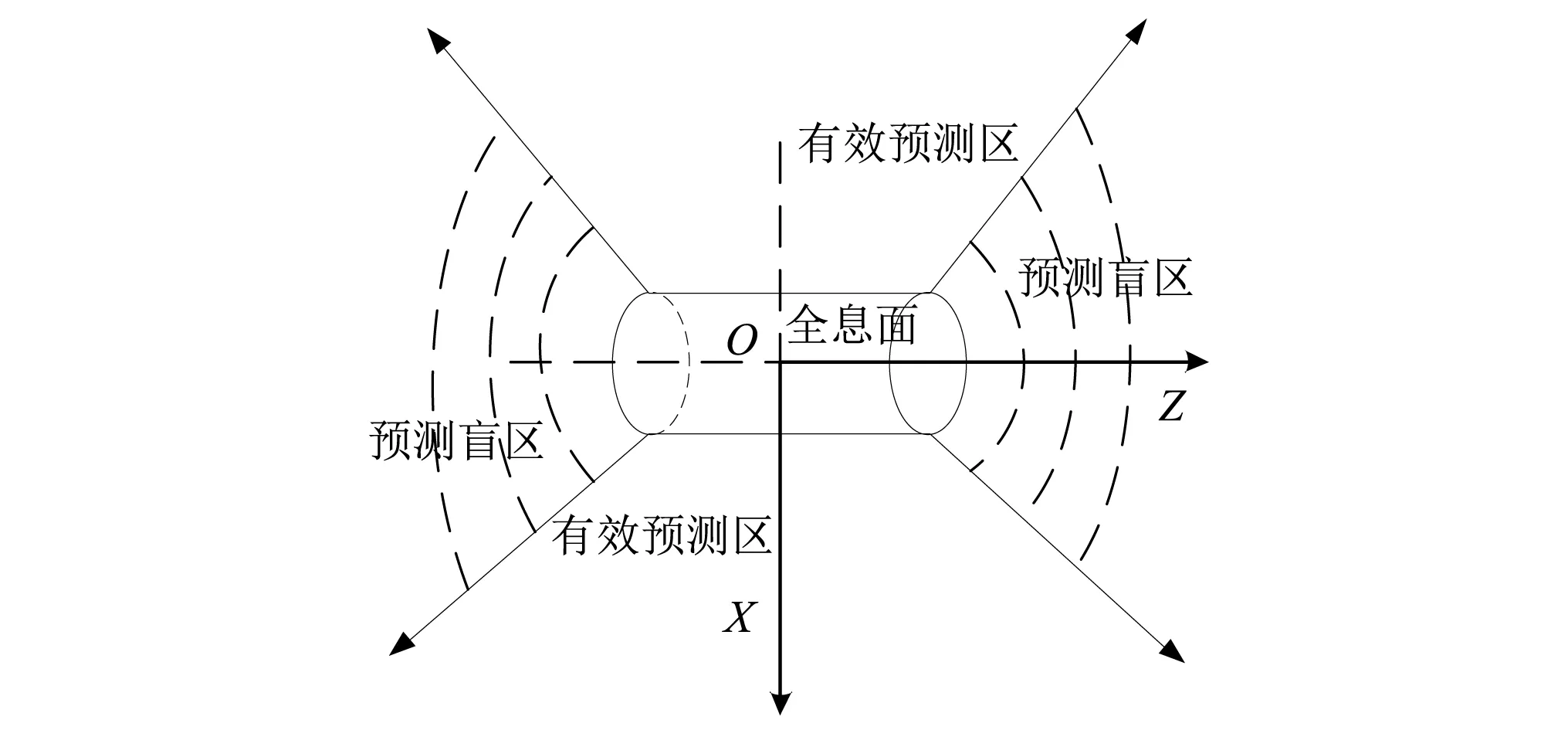
图7 有效预测范围Fig.7 Effective prediction range

图8 船舶有限元模型Fig.8 Ship finite element model

全息柱面为rH=4 m，0<φH<2π， -30 m≤zH≤30 m；dz=2 m，dφ=π/18；通过远场声压数据进行参数匹配，获取模态展开法参数如下：最大模态阶数M=14，N=10，轴向截止波数kz max=1.5。全息柱面声压云图及XOZ平面场点声压云图，如图9、图10所示。其中模型位于坐标原点O，船艏与Z轴正向同向。

图9 船舶全息面声压云图Fig.9 Sound pressure nephogram of ship holographic surface

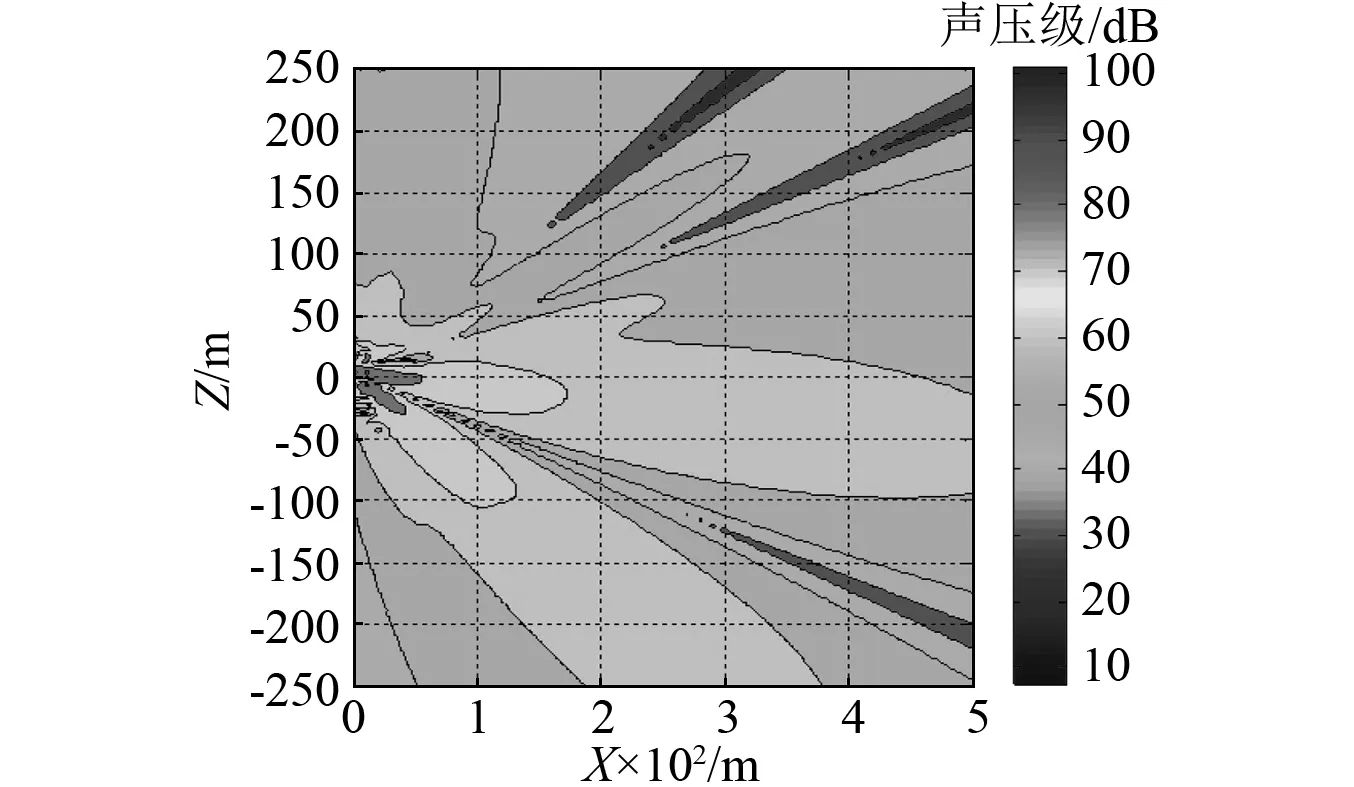
图10 XOZ平面声压云图Fig.10 Sound pressure nephogram of XOZ plane

图11为通过全息面声压和振速数据进行XOZ平面声源级预测。由图11可知，基于振速的预测算法要优于声压，-80°～0°方向的声源级重建值与理论值相比较为精准，0°～80°方向的声源级有一定误差。这是由于激励点1位于模型中部，此处模型为规则圆柱形结构体，其表面振动按照圆柱径向方向辐射。而激励点2位于模型中前部，此处模型为椭圆柱形结构，其表面振动并非按照圆柱径向方向辐射，因此导致0°～80°方向的声源级预测产生偏差。

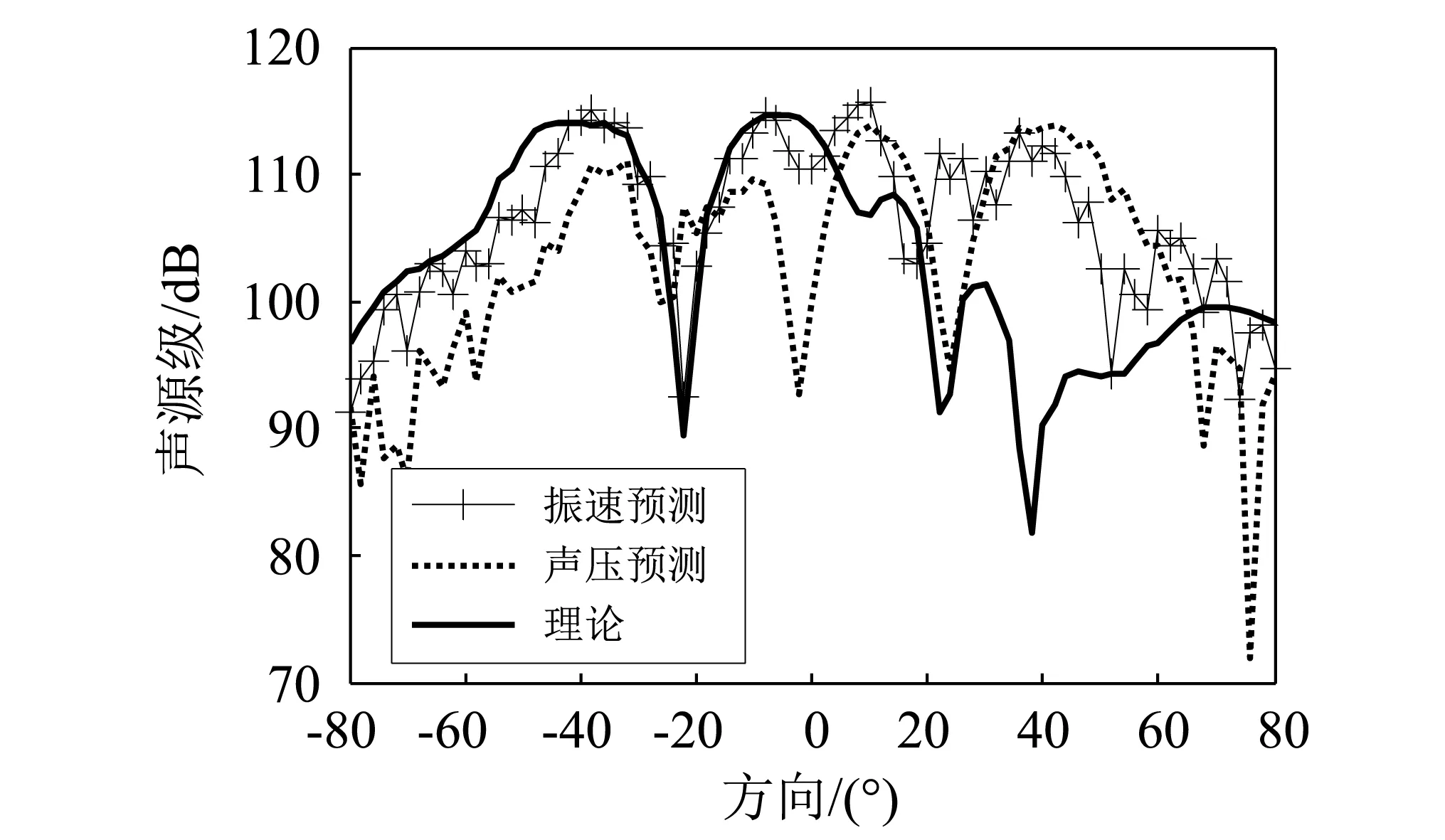
图11 XOZ平面预测声源级Fig.11 Predicted sound source level of XOZ plane

图11与图6中圆柱体的声源级预测结果相比，船舶模型在尾部方向的声源级预测较为精准，这是由于船舶模型存在多个舱段和肋板，振动模态及振动传递路径与单层圆柱壳有很大区别，质量和刚度的非均匀性使船舶仅在激励点局部引起较强的振动与声辐射，首尾振动产生的辐射声压较小，全息孔径远大于主要辐射面，因此预测范围较大。

3 试验验证

由于消声室截止频率较低，测点布放方便，且传声器的一致性较好，因此在消声室中进行了圆柱声源的声场预测试验，验证本文提出“基于模态展开法的声场预测”算法的正确性。消声室截止频率80 Hz，自由声场半径大于1.5 m，本底噪声小于41 dB。实验设备布放及环境如图12和图13所示。圆柱体半径0.175 m，长度0.83 m，在其内部布放一个激振器，其型号为南京佛能公司的HEV-50型，最大激振力50 N，信号带宽0～3.5 kHz。在圆柱表面布放一个同轴18阵元的传声器环形阵列，传声器周向间隔为20°，环形阵列半径0.225 m，同时距离圆柱体轴心0.675 m处布放24阵元的直线阵列作为对照组，阵元间隔为0.1 m。通过扫描法进行圆柱体表面全息面的复声压数据采集，即将环形传声器阵列沿轴向每隔0.1 m平移测量一次，得到扫描信号，由于24元直线阵固定不动，与圆柱声源保持一定的相位关系，因此从中选择一个参考信号，将扫描信号与参考信号进行互谱计算，从而获取全息面的相对相位。

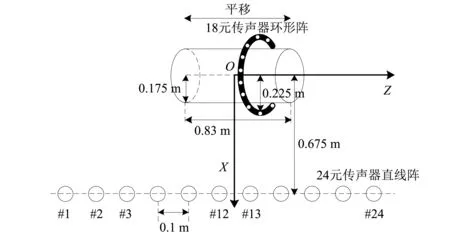
图12 实验布放图Fig.12 Schematic diagram of experiment platform

图13 消声室实验环境图Fig.13 Anechoic chamber experimental environment

全息柱面为rH=0.255 m，0<φH<2π，-0.4 m≤zH≤0.4 m；dφ=π/9，dz=0.1 m，模态阶数M=10，N=10，轴向截止波数kz max=30。

图14为XOZ平面rS=0.675 m，φS=π，-2 m≤zS≤2 m处的声压级预测值与测量值对比结果。可看出随着激振频率的增加，XOZ平面上辐射旁瓣变多，而“基于模态展开的辐射噪声预测”算法有效的进行辐射声场的预测，预测声压级曲线波峰处的误差小于3 dB，但由于全息面与预测面距离圆柱体较近，圆柱体首尾两端方向的声压级预测存在一定误差，这与“2”节仿真结果一致。

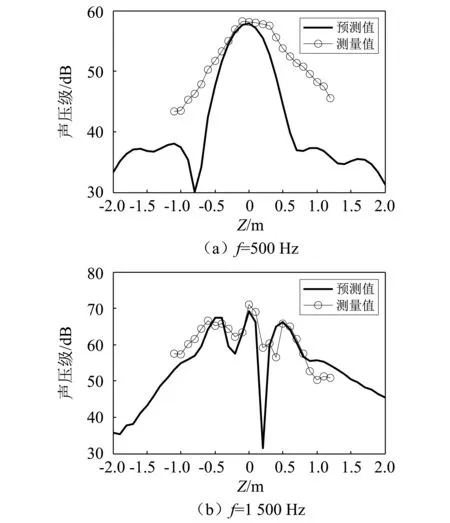
图14 XOZ平面的预测声压级Fig.14 Predicted sound pressure level of XOZ plane

4 结 论

为了实现圆柱体的辐射声场预测，本文提出了“基于模态展开的辐射噪声预测”算法，将圆柱体在介质中的径向位移用轴向及周向模态表示，并将其作为径向振动的基函数，建立传递函数矩阵，通过求解不同基函数的权系数来获取任意位置的声场。在此基础上通过远场声压数据进行最小二乘意义下的最优参数配置方法，减小了传播波数与倏逝波数在辐射圆附近幅值突变产生的重建误差，提高了结构体远场预测精度。通过脉动球声源及圆柱体声源的仿真分析与消声室试验，验证了理论推导的正确性，具体结论如下：

(1)利用有限长度的轴向模态波数构造基函数，在预测声场时全息孔径以外的范围不会出现“虚像”， 扩大的圆柱体远场预测范围。

(2)当全息孔径有限时，全息面边缘处的声源信息丢失较多，数据的不连续性较为严重，圆柱体首尾部方向声源级预测存在较大误差，沿圆柱径向扇形范围内声源级预测较为精准。

(3)当全息孔径大于主要辐射面，如含有舱段和肋板的船体模型，激励点仅在局部引起较强的振动与声辐射，此时声场预测范围较大，但当辐射面为非规则圆柱模型时，预测会产生一定误差。