考虑套管边界和液柱高压的射孔液压力脉动规律分析

李明飞， 窦益华， 曹银萍， 于 洋， 曹 亭

(西安石油大学 机械工程学院，西安 710065)

当前射孔工艺不断追求大孔径、高孔密射孔，将增加射孔总的爆轰能量，引起射孔液强烈波动及射孔段管柱剧烈振动，国内西部陆上油田和美国Fort Worth盆地[1]、Arkoma盆地[2]、墨西哥湾[3]等的油气开采也遇到射孔事故。为此，有必要探寻射孔液压力脉动规律，为射孔段管柱动力响应和安全性分析提供依据。

文献[4]对爆距不大于4 倍炸药半径范围内的钢板进行了水下爆炸试验，分析了近距接触冲击波的传播以及与气泡的相互作用。文献[5]利用高速相机，测量水中爆轰近场冲击波，根据冲击波的扫描轨迹求得冲击波阵面压力，并外推冲击波的初始压力，用LS-DYNA分析了柱形装药近场压力沿轴向的衰减规律。

文献[6]对射孔管柱进行了应力强度和瞬态响应分析，得到了管柱位移、速度、加速度、应力等对射孔冲击载荷的影响规律。文献[7]对深水自由场、近自由液面、近刚性壁和弹性边界等不同边界条件下的水下爆炸气泡动态特性进行了仿真分析。文献[8]对复杂边界近场水下气泡脉动规律进行了实验研究，通过高速摄影以及对流场参数、表面压强和变形响应量的测量，分析了复杂边界的近场气泡的压力脉动特性。文献[9]采用铜丝电极低电压条件下打火生成气泡的方法，配合高速摄影技术，研究了两平行板间与筒状区域构成的对称边界附近气泡的脉动特性。文献[10]采用数值模拟方法，分析了爆轰冲击下深水圆柱的动态响应，分析了破坏程度与水深之间的关系。文献[11-12]应用有限元二维分析方法，模拟了爆轰波叠加和干扰对射流偏转角的影响，关注点为射流偏转角。

综上所述，射孔液压力脉动是水下爆炸的特殊课题，与传统水下爆炸相比，具有爆点距液面深、静液柱压力大、狭长小空间边界限制等差异，使得射孔液压力脉动分析与传统的近液面、小压力和自由及半自由水下爆炸区别很大，传统研究成果无法直接应用，需要开展针对性研究。本文考虑相变界面冲击波传播的连续性，基于Tait方程，建立冲击波初始压力分析方法；考虑套管狭长边界条件限制，阐明冲击波传播规律，构建直达冲击波分析方法；基于波的反射原理，建立套管交界面、射孔液参数的近似图解和波反射的分析方法；应用直达和反射波的叠加原理，建立压力脉动分析方法。

1 爆距对冲击波峰值压力影响分析

爆距为0～6倍球形装药半径的爆轰即为接触爆轰，冲击波直接作用于套管内壁面。赵继波拟合了实验数据，建立了TNT柱形装药水下冲击波传播距离与时间变化关系的公式

(1)

式中：c0为水中声速，1.5 km/s；Ai为拟合系数，表征冲击波强度；Bi为拟合系数，表征冲击波衰减时间；D为TNT炸药爆速，D=6.8 km/s。

文献[13]应用LS-DYNA软件模拟了水下爆轰压力沿轴向的衰减曲线，拟合得到了水下轴向爆轰压力衰减方程

pm=ph+12.02e-0.031x,x<140 mm

(2)

式中：ph是稳定后的压力，ph=0.23 GPa。

假设柱形装药高为h1，球形装药半径为r，R=1/4h1=1/3r，r=3/4h1。高达数千米的射孔液静液柱压力为爆轰前初始压力，记为P0，为冲击波最终衰减值，Patm为大气压。假设原始深度为h，则初始压力为

P0=Patm+ρgh

(3)

代入(1)和式(2)，得到位移随时间变化以及压力峰值和距离关系的公式

(4)

pm=p0+pxe-0.031(R-1/3r)

(5)

式中：pm为爆距R处的压力峰值，GPa；px为射冲击波的初始压力，GPa。

对式(1)求导，即可得到波阵面速度随时间变化的关系式

(6)

式中：us为波阵面速度，km/s；n=2；A1=7.2；B1=7.5×10-2；A2=4.9×1010；B2=7.8×10-13。

根据式(4)，借鉴根据TNT水中爆炸冲击波峰值的相似律定理[14]，可计算近、中远场冲击波压力峰值Pm

(7)

式中：R为爆距，m；K与α值与比例距离r有关，12≤r<240，K=5.2×107，α=1.13，6≤r≤12，K=4.4×107，α=1.50；m为装药质量，kg。

以TNT球形装药为例，r=14 mm，装药质量为18.1 g，静液柱压力P0=65 MPa，冲击波初始压力Px=4.1 GPa，分别代入式(4)和式(6)，分析各点处峰值压力，结果如图1所示。代入式(7)，分析波的传播速度，代入式(4)分析冲击波到达时间，结果如图2～图 4所示。r=4.5，峰值压力为0.75 GPa，位于离射孔弹最近套管内壁面与射孔液界面处，随后，压力随爆距增大先迅速减小到0.2 GPa，之后减小速度趋于平缓，并最终恢复到P0。由图3可知，波阵面传播速度最大值为4.17 km/s，也出现在r=4.5处，随着爆距的增加迅速下降到1.79 km/s，保持稳定。由图4可知，r=4.5处，冲击波到达时间为22.7 μs，随爆距增大而增长。

图1 依据爆距划分爆轰类型示意图Fig.1 Schematic diagram of detonation type explosion distance

图2 冲击波峰值压力与比例距离关系曲线Fig.2 The variation of peak pressure of shockaccording waveto with proportional distance

图3 波阵面传播速度随爆距变化规律Fig.3 The variation of wave front propagation

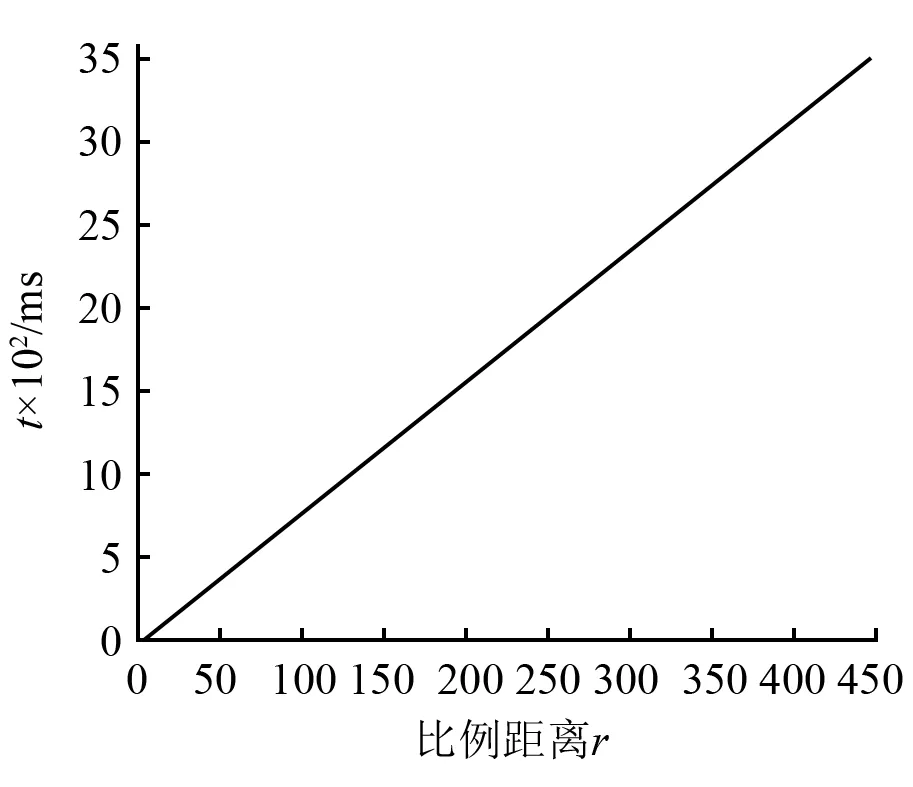
图4 时间随爆距的变化规律Fig.4 The variation of time with velocity with proportional distanceproportional distance

2 套管界面冲击波反射规律分析

若冲击波由甲物质传播到乙物质，将从交界面向入射物质中反射冲击波或稀疏波[15]。当乙物质密度明显小于甲物质，即比甲物质“软”时，传播稀疏波，反之，则传播反射波。两种情况的速度和压力变化如图5所示[16]。

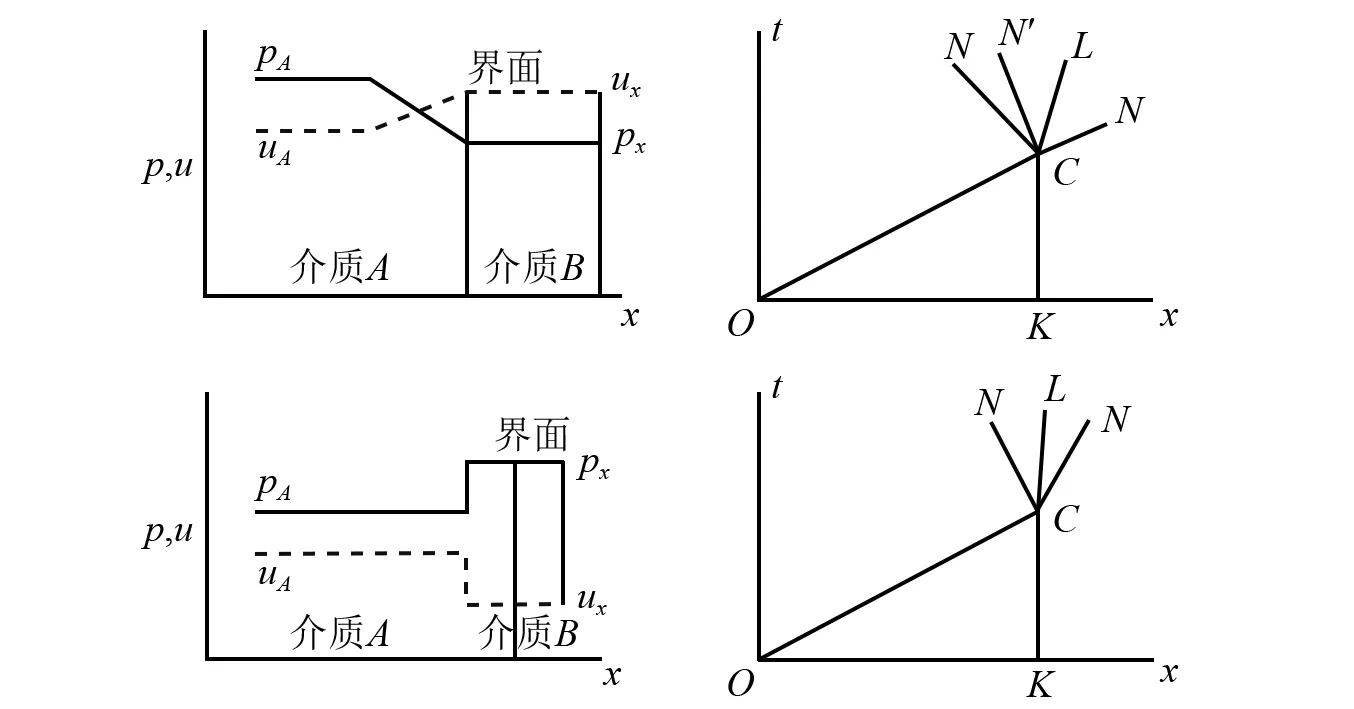
图5 冲击波渡越时的速度和压力图Fig.5 Speed and pressure map of a shock wave when passing through a mediummedium interface

若两介质的冲击绝热线已知，在(p，u)平面，绘制两介质的p(u)曲线C和M(或N)。如图6所示，点a表示物质甲中的入射冲击波参数，即u=ua，p=pa。物质乙的冲击绝热线位于物质甲下方，反射波为稀疏波，即为N曲线，表现为b点处压力减小， 速度增大； 反之则得到M曲线，表现为d点处压力增大，速度减小，反射波是冲击波。使用matlab拟合图4曲线，建立冲击波传播时间和爆距的公式

t=8×r-30

(8)

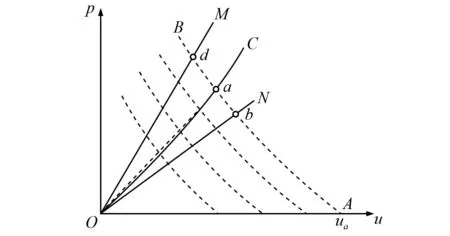
图6 确定冲击波分界面时初始参数近似图解Fig.6 Approximate diagram of initial parameters for determining the shock wave crossing

式中：r为比例距离，满足精度的取值为0≤r≤26.3。

已知物质的冲击绝热线的形式为

D=a+λu
或D=a+λu+λ0u2

(9)

射孔液中冲击波阵面上冲击波速度DⅡ可根据式(10)计算，式中系数如表1所示。

(10)

表1 冲击绝热线式(10)的系数

冲击波阵面处的质量和动量守恒方程为

ρ0D=ρ(D-u)

(11)

P-P0=ρ0uD

(12)

式中：ρ为波阵面上的介质密度，g/cm3；ρ0为物质初始密度，g/cm3；D为冲击波速，km/s；u为波阵面上的粒子速度，km/s；P为波阵面上的压力，GPa；P0为波阵面前的压力(P0≪P时可以忽略P0)，GPa。

联立式(9)和式(11)可得波阵面上粒子速度和压力关系

(13)

将式(8)代入式(11)中可得P=P(u)形式的冲击绝热线方程

P-P0=ρ0(a+λu+λ0u2)u

(14)

如图7所示，根据式(13)绘制射孔液的冲击绝热线。射孔液压力为静液柱压力，波阵面上的粒子速度为0，随压力升高，粒子速度增大，压力达到最大值0.75 GPa，粒子速度达到322 m/s。由图8可知，冲击波在套管中传播时，波阵面压力与粒子速度成正比。

(15)

将式(15)代入式(14)中，可得P=P(ρ)形式的冲击绝热线方程

(16)

因为比容v=1/ρ，可以得到P=P(v)形式的冲击绝热线方程

(17)

式中：v为冲击波阵面后比容，cm3/g；v0为冲击波阵面前比容，cm3/g。

将射孔液参数代入式(17)，在(p，v)平面绘制射孔液等熵卸载线，如图9(a)所示。v=0.77 cm3/g、密度为1.3 g/cm3时，射孔液压力为65 MPa，说明射孔液未压缩，与实际情况相符。v=0.5～0.6 cm3/g处，冲击波压力逐渐增大，射孔液密度迅速增大，说明射孔液压缩到一定程度时，所需压力也迅速增大。v<0.5 cm3/g时，射孔液压力随比容下降而下降，说明在v=0.5 cm3/g处，射孔液的流体性质发生了改变。实际应用中，可取v=0.5～0.6 cm3/g的等熵卸载线，如图9(b)所示。

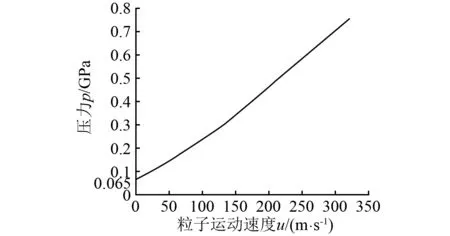
图7 射孔液的冲击绝热线图Fig.7 Perforating liquid impact insulation diagram

图8 套管冲击绝热线图Fig.8 Casing impact insulation diagram

图9 射孔液的等熵卸载线Fig.9 Perforating fluid isentropic unloading line

pr=pA-pB

(18)

如图11所示，采用表1和表2的值，运用式(16)和式(17)，绘制冲击波由射孔液传到套管内壁面的近似图解，依据图10原理分析反射波大小，分析结果如表3所示。离射孔弹最近套管处的爆距为62.3 mm，由式(16)分析求得峰值压力为75 MPa。根据式(14)，求得射孔液波阵面上粒子速度uA=0.32 km/s，即为图11(a)中的A点，过A点作P=P(v)曲线下半支曲线1，再作曲线2，曲线2关于射孔液的p=p(u)曲线对称。曲线2与套管P=P(u)曲线相交在B点，即为交界面处波阵面状态参数对应的点，压力为3.8 GPa，速度uB=0.13 km/s。随爆距增大，交界面处速度、压力和反射能越来越小。R=307.7 mm处，反射波压力Pr=50 MPa，低于65 MPa，说明R=307.7 mm时，套管的反射作用可忽略，说明16孔/m射孔，某一射孔弹周围的4颗射孔弹将会对该射孔弹产生影响，其余远端弹的作用可忽略。

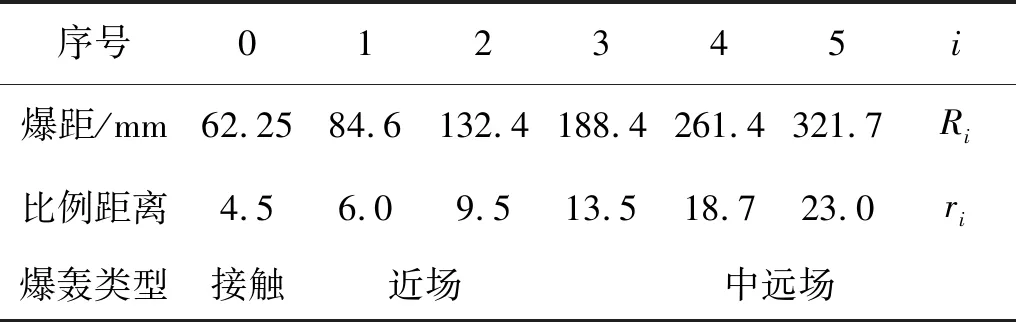
表2 爆距和比例距离表

图10 由低动力学阻抗传入高动力学阻抗物质的冲击波传播示意图Fig.10 Schematic diagram of shock wave propagation from low dynamic impedance medium to high dynamic impedance medium

表3 不同爆距对应的冲击波参数

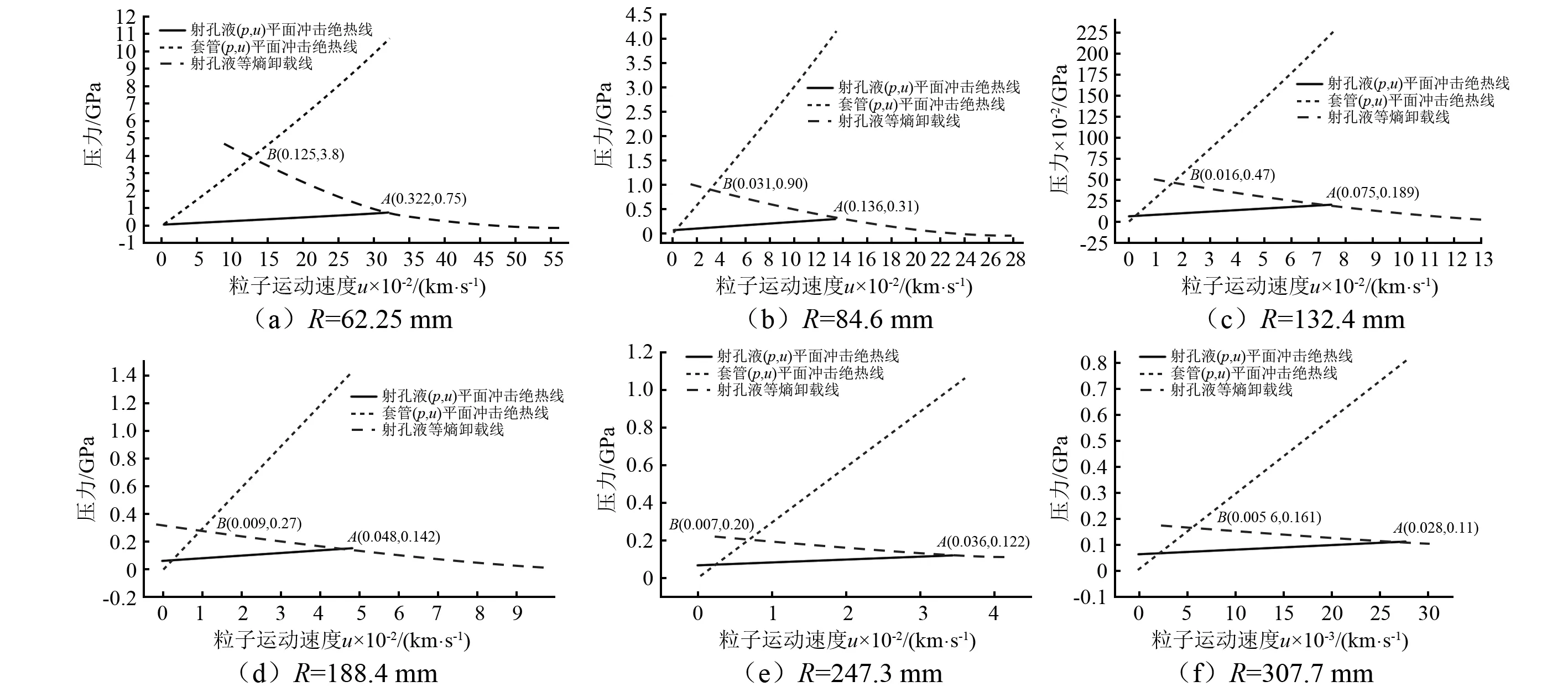
图11 射孔液和套管交界面上冲击波参数近似图解Fig.11 Approximate diagram of shock wave parameters at the interface between perforating fluid and casing

3 考虑冲击和反射波叠加射孔液的压力脉动分析

根据文献[17]提出的的爆轰载荷阶段划分，射孔压力脉动曲线可分为：①原始静液柱压力阶段；②指数形式衰减阶段，压力迅速衰减到1/3峰值；③倒数形式衰减阶段，衰减速率明显减缓，该阶段压力很小，变化幅度也很小，近似认为此段区域压力为0。冲击波到达某点时，压力瞬间跳跃到峰值，并以指数函数降低至峰值的1/3，衰减系数为θ。此阶段射孔液中任一点的压力为

P(t)=Pm·e-t/θ, 0≤t≤θ

(19)

式中：时间衰减系数θ由试验确定，或由式(20)计算确定

(20)

式中：r0为装药半径，m；c=1 500 m/s为射孔液中声速。

从1/3压力峰值降低到初始压力阶段，压力随时间变化关系的公式为

(21)

其中，各参数计算公式为

(22)

爆轰冲击波对射孔液的冲击和扰动，使射孔液发生压力脉动，射孔液压力脉动是水下爆炸的特殊课题，与传统水下爆炸相比，具有爆点距液面深、静液柱压力大、狭长小空间边界限制等差异，使得射孔液压力脉动分析与传统的近液面、小压力和自由及半自由水下爆炸区别很大，传统研究成果无法直接应用，有必要开展针对性研究。需考虑接触、近和中远场爆轰的不同，需考虑套管内壁面反射作用，需考虑冲击波反复叠加作用。如图12所示，给出了射孔液与套管交界面处0号弹的射孔压力脉动分析图，该点压力包括0号弹冲击波的反射压力脉动P0(t0)，也包括1～4号弹发出的强冲击的反射波Pri(i=1,2,3,4,)，还包括该点处叠加压力脉动Pi(ti) (i=1,2,3,4,)，因此，该点的射孔压力脉动用式(23)分析

P0(t0)=Pr0·e(-t0/θ),t0=0～8.3

P1(t1)=[P0(t=8.3)+Pa1]·e(-t1/θ),t1=0～23

P2(t2)=[P1(t=23)+Pa2]·e(-t2/θ),t2=0～31

P3(t3)=[P2(t=31)+Pa3]·e(-t3/θ),t3=0～33

P4(t4)=[P3(t=33)+Pa4]·e(-t4/θ),t4>0

P(t)=P0(t0)+P1(t1)+P2(t2)+P3(t3)+P4(t4)

(23)

式中：Pr0=3.05 GPa，为0号弹反射压力；θ=12.3 μs，为时间衰减常数；Pai的值可根据宗智研究中的方法求得，为第i号弹冲击波的反射压力。

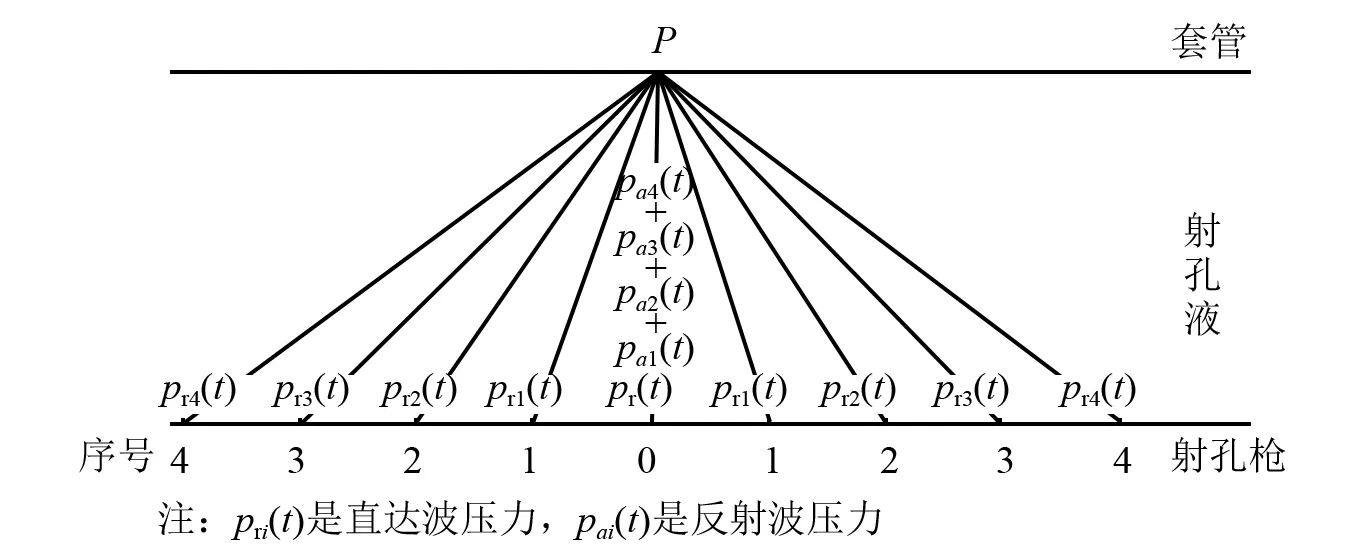
图12 射孔液与套管交界处正面射孔液压力脉动分布图Fig.12 Analysis of the pressure pulsation of the front perforating liquid at the interface between the perforating liquid and the casing

式(23)的计算结果如图13所示，当冲击波到达该点时，压力瞬间达到3.05 GPa，随后以指数形式高速衰减，再以倒数形式衰减，最终恢复为初始压力65 MPa。图14给出了1～4号弹产生的冲击波对压力脉动的影响曲线图，14.4 μs时，0号弹冲击波到达，压力瞬间达到3.05 GPa，随后以指数函数衰减至1.7 GPa，22.7 μs时，1号弹冲击波到达，在套管内壁反射后叠加，压力为Pa1，随后Pa1追上p0(t)卸载部分，压力达到2.3 GPa，再次以指数函数衰减，2～4号弹的影响与1号类同。对比考虑和不考虑弹间干扰和叠加的压力脉动曲线，爆轰波的干扰和叠加使得射孔液压力存在数个波峰，增大了压力脉动振幅和峰值；另外，单射孔弹时压力恢复到初始压力的时间为60 μs，多射孔弹时为90 μs，压力恢复时间增长了30 μs，说明叠加作用增加了压力脉动的强度。

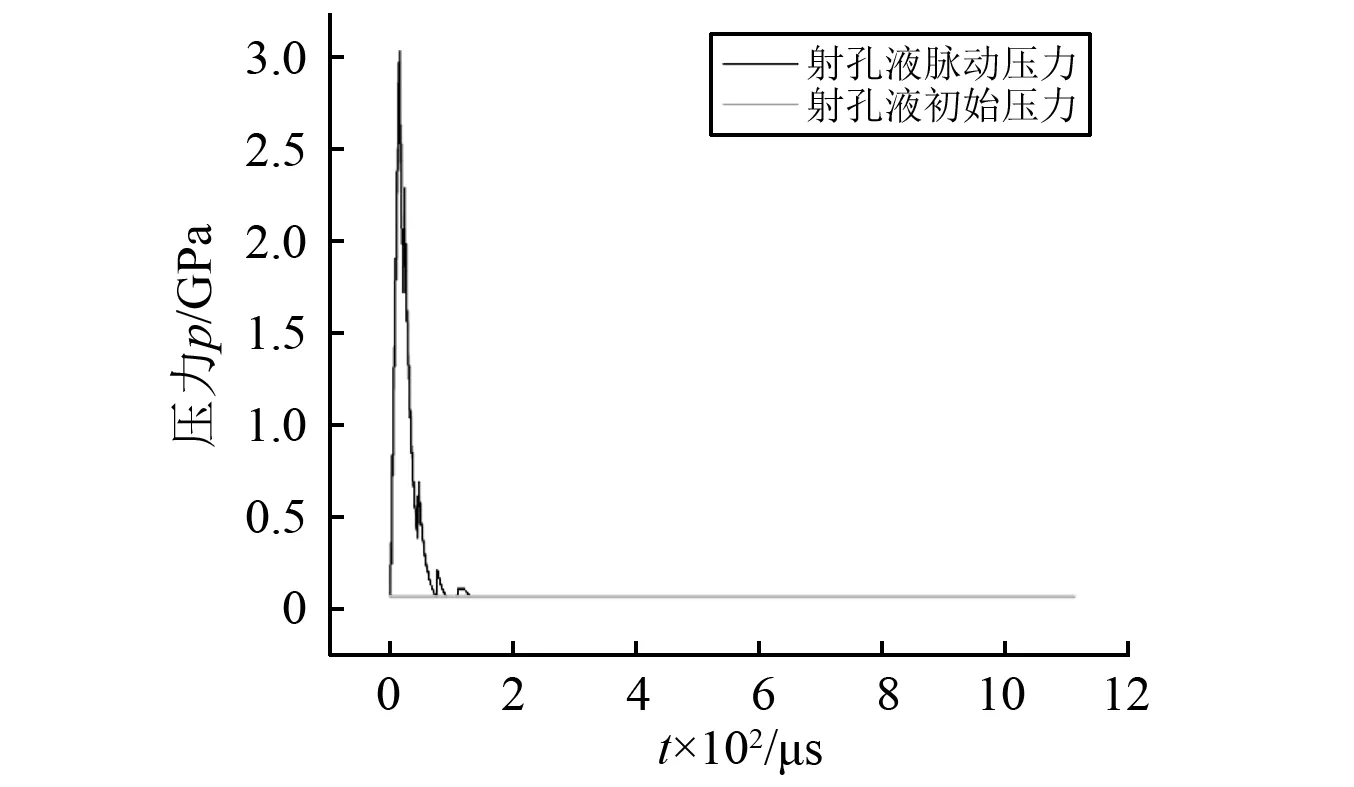
图13 射孔液与套管交界面处正面射孔液压力脉动规律图Fig.13 Pressure pulsation diagram of the front perforating liquid of perforating bullet at the interface between perforating liquid and casing

图14 1～4号射孔弹产生的冲击波对射孔液压力脉动的影响规律图Fig.14 The effect of shock wave generated by perforating bullets 1—4 on perforating liquid pressure pulsation

考虑到常用射孔枪弹间结构的相似性，图14中的射孔液压力脉动规律可为常规的射孔枪弹组合下射孔的压力脉动分析提供参考。式(23)即为考虑爆点距液面深、静液柱压力大、狭长小空间边界限制、反射和叠加的射孔液压力脉动分析公式，可为射孔管柱的动力响应和动力强度安全、射孔时封隔器的密封及完整性分析提供依据。

4 结 论

本文建立了冲击波初始压力分析方法，建立了冲击波传播规律研究方法，得到了直达冲击波理论分析方法，构建了射孔液、套管交界面参数的近似图解和反射波的理论分析方法，考虑反射和叠加，阐明了射孔液压力脉动规律，得到以下结论。

(1)考虑射孔井的深液面下爆轰、高静液柱压力特点，建立了爆轰产物向射孔液扩散形成冲击波的初始压力分析方法，并经实例井验证。

(2)考虑套管狭长边界条件限制，阐明了冲击波传播规律，构建了直达冲击波分析方法；基于波的反射原理，建立了套管交界面、射孔液参数的近似图解和波反射的分析方法，实例分析表明，峰值压力可达0.75 GPa级别，波阵面速度可达4.17 km/s级别，随爆距呈指数衰减至初始压力值65 MPa，冲击波阵面传播时间与爆距呈正比。

(3)构建了射孔液、套管交界面参数近似图解法和反射波理论分析方法。实例分析表明，反射波压力明显大于入射波，并随爆距增大而减小。某一射孔弹周围的4颗射孔弹将会对该射孔弹产生影响，其余远端弹的作用可忽略。

(4)考虑套管内壁面的反射和波间干涉，建立了完整的聚能射孔压力脉动规律分析方法，并根据实际生产井的参数，分析了该井的射孔压力脉动曲线，对比分析考虑和不考虑弹间影响的压力脉动，弹间影响使得射孔液压力存在多个波峰，增大了压力脉动振幅和峰值；另外，多弹射孔较单枚射孔压力恢复到初始压力的时间增长了30 μs，说明叠加作用增加了压力脉动的强度。