玻-碳混杂纤维缠绕复合材料发射筒发射动力学研究

2019-12-31孙同生于存贵

振动与冲击 2019年24期

孙同生，王琪，于存贵

(1.南京理工大学机械工程学院，南京 210094；2. 江西长江化工有限责任公司，江西九江 332006)

某动能破门弹武器系统采用平衡抛射技术，能在有限空间发射。发射时两个闭气活塞受到膛内火药燃气压力的作用，推送弹丸及平衡体沿筒体轴线反向运动，活塞达到筒体两端时被制动，火药燃气被密闭在筒体内，实现“微声、微光、微烟”的微痕发射。

采用玻-碳混杂纤维缠绕而成的复合材料发射筒是该武器系统的重要部件之一。目前，对于复合材料发射筒的研究，徐光磊等[1-2]考虑混杂效应对纤维混杂缠绕发射筒三维等效模量进行了理论计算和试验研究，给出了考虑混杂效应的纤维多向缠绕筒等效模量计算方法。尹冬梅等[3-4]利用ANSYS中的APDL二次开发语言，考虑缠绕预应力对轨道炮身管复合材料外壳进行渐进损伤分析。结果表明在电磁载荷作用下身管复合材料外壳会出现分层损伤。朱孙科等[5-6]利用有限元显式动力学模拟了导弹的发射过程，并采用非支配排序遗传算法对复合材料发射筒的铺层角度和铺层厚度进行了优化。文献[7-8]采用有限元法对复合材料发射筒的刚强度进行了建模，模型中以均布载荷的形式施加燃气流作用力，没有考虑燃气流冲击以及弹-管接触碰撞引起的动态效应，计算结果与实际情况误差较大。

在弹丸发射过程中，复合材料发射筒既要承受火药燃气压力的强冲击载荷作用，又要承受较大的轴向制动力作用，整个过程存在较强的接触碰撞与动态冲击效应。Tzeng[9-10]研究了带金属内衬的复合材料圆筒的动态应变响应。杨宇宙[11]采用多物质任意拉格朗日-欧拉方法和自动接触算法对带金属内衬的复合材料身管在弹丸冲击载荷作用下的弹性应力波传播过程进行了数值模拟，揭示了压力前缘沿身管轴向移动时应力应变幅值的发展规律，以及伴随应力波传播而产生的共振效应。徐亚栋[12]利用有限元法分析了带金属内衬的复合材料身管的模态响应和瞬态动力学响应，并对复合材料身管的强度进行校核。魏存磊等[13]对瞬态压力冲击载荷与热冲击载荷作用下带金属内衬的复合材料身管损伤进行数值模拟，研究了不同结构设计参数对复合材料身管损伤的影响。现有的关于复合材料发射筒发射动力学的研究主要是针对带金属内衬层的火炮身管，并且大多数文献在研究过程中并没有严格按照弹丸实时轴向位置来定义火药燃气压力在发射筒内的空间分布，不能准确模拟实际发射环境下复合材料发射筒的受载情况。

本文考虑玻-碳混杂纤维缠绕复合材料发射筒内火药燃气压力二维瞬态分布特性，采用罚函数法和面-面自动接触算法模拟实际发射时各关键部件间的复杂接触碰撞过程，建立了弹-管耦合非线性动力学模型。借助有限元用户自定义子程序，自动读取两侧活塞轴向实时运动位置，实现了火药燃气压力二维瞬态分布与弹丸运动相互关联的动力学过程，真实地模拟了玻-碳混杂纤维缠绕复合材料发射筒受到的强动态冲击效应。数值分析结果与实弹射击试验对比，验证了数值模型的准确性。本文提供的建模方法可以更准确地评估纤维缠绕复合材料发射筒的发射安全性。

1 理论模型

1.1 动态接触碰撞模型

某动能破门弹在发射过程中，各关键部件之间存在复杂的接触碰撞，并且伴随着材料的塑性变形，因此接触边界会随着材料的塑性变形而发生改变，属于复杂的动边界非线性接触碰撞问题。在求解这类问题时，除了平衡方程、几何方程、本构方程、初始条件和边界条件以外，还需要满足接触边界条件[14]。采用有限元方法将系统离散后得到其动力学控制方程

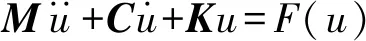
(1)

式中：M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵。根据文献[15]，动接触边界条件可以离散为

(2)

式中：ut为t时刻节点位移向量；Bn,Bτ为接触约束矩阵；D0为初始法向接触间隙。上述接触边界条件可以合写为

Bu-λ≥0

(3)

式中:B取Bn或Bτ；λ取-D0或Bτut。

用罚函数法将上述接触边界条件引入动力学控制方程，可以把接触问题转化为求解带约束泛函的极值问题[16]，即

(4)

式中:πi为第i个部件的势能;Sc为接触面;α为罚因子。采用虚功原理并进行有限元离散后，得到带罚因子的动态接触问题动力学控制方程

(5)

1.2 弹丸膛内运动力学模型

依据欧拉-伯努利梁理论[17-18]，本文所研究的用于平衡抛射的复合材料发射筒可以简化为内部承受火药燃气压力、弹丸/平衡体移动质量和动态接触碰撞力的简支梁模型，如图1所示。图1中，M1,M2为弹丸和平衡体的质量，M1=M2，即为等质量等行程平衡抛射；Fcon为计及阻尼和惯性效应时的接触碰撞力，vt为弹丸/平衡体的实时运动速度。弹丸、平衡体与发射筒所围成的空间为火药燃气作用区域，火药燃气压力随弹丸的运动而发生强动态变化。

图1 发射筒受载简化示意图Fig.1 The loading schematic diagram for launch canister

根据达朗贝尔原理[19]，计及阻尼和惯性效应时，在移动弹丸以及火药燃气压力作用下复合材料发射筒受到的载荷为

F=δ(x-u(t))Fcon+∑δ(x-u(t))P(x,t)du

(6)

(7)

(8)

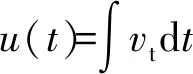
2 弹-管耦合动力学建模

2.1 有限元模型

对复合材料发射筒主要部件进行适当简化并离散，建立有限元装配模型，如图2所示。主要包括玻-碳纤维混杂缠绕复合材料筒体、连接环、变形环、制动环、活塞、弹丸和平衡体等，由于本文不研究拉断体的拉断过程，故在有限元模型中将其处理为显示体，其提供的拉断力通过给连接单元施加相应大小的闭锁力来模拟。

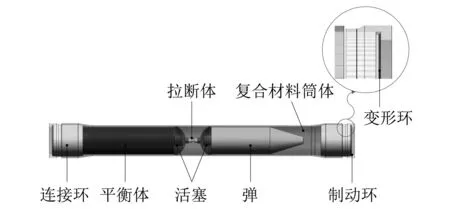
图2 有限元装配模型Fig.2 The assembly model of FEA

复合材料筒体为纤维缠绕而成的薄壁结构，采用SC8R连续壳单元进行离散，其他部件采用等参六面体单元进行离散。弹丸与平衡体的变形不是主要研究对象，故将弹丸与平衡体作刚性化处理。此外，考虑发射时各部件间的接触碰撞运动关系，按实际情况在活塞侧面与复合材料筒体内表面、活塞端面与变形端面、活塞与弹丸/平衡体、变形环与活塞内表面、变形环与制动环之间施加接触碰撞，均采用罚函数法和面-面自动接触算法进行处理，以模拟真实的动态发射过程。

2.2 筒体材料参数

筒体原材料为高强玻纤S4C9-960/环氧-酸酐树脂体系和T700/环氧-酸酐树脂体系，通过试验获得两种材料体系的各向异性力学性能参数如表1所示。

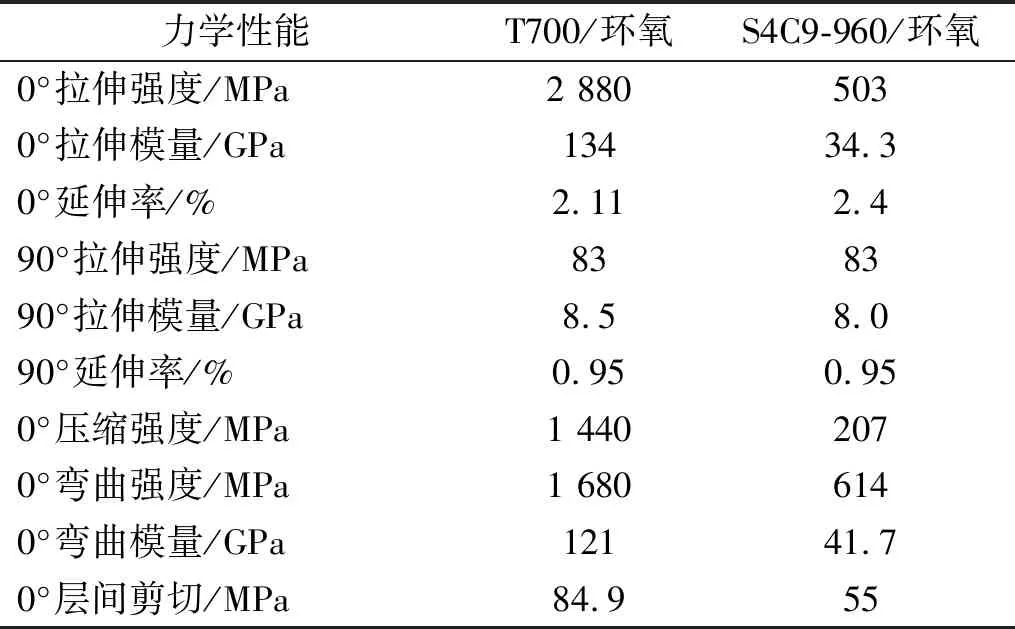
表1 筒体材料力学性能参数

筒体由上述两种材料体系经环向和纵向交替缠绕固化而成，环向层与纵向层共计20层，各层厚度相同。其详细的铺层设计如表2所示，其中90°缠绕角为环向缠绕。

由于纤维复合材料具有明显的各向异性，因此需创建局部材料坐标系，并根据上述实际铺层数参数赋予筒体材料属性。有限元模型中复合材料筒体的铺层结构如图3所示。从图3可知，左下角坐标系代表局部柱坐标系，其1方向沿筒体轴线方向，2方向沿筒体周向，3方向沿筒体径向。各层厚度t=1表示相对厚度，并不代表实际意义上的厚度。各层上的斜线表示纤维方向，可以看出，第3～11层、第14层、第17层、第20层纤维方向与局部坐标系的2方向一致，表示纤维沿环向缠绕，有限元模型中的复合材料铺层方式与实际结构完全相同。

表2 复合材料筒体铺层设计

图3 有限元模型中复合材料筒体的铺层顺序Fig.3 Layup sequence of composite launch canister in FEA model

2.3 子程序实现火药燃气压力动态加载过程

试验测得膛内压力随时间和活塞位移量变化规律如图4所示。从图4可知，弹丸与平衡体膛内运动伴随着火药燃气压力值以及筒体受载区域的动态变化，即火药燃气压力呈现二维瞬态分布特性。本文采用在活塞有效受力面上施加膛内压力的加载方式，模拟活塞推动弹丸和平衡体的膛内运动过程，并利用有限元软件提供的Vdload动载荷子程序接口，通过实时读取两侧活塞轴向位移量来定义复合材料筒体内表面受载区域，准确模拟火药燃气压力在复合材料筒体内的二维瞬态分布特性。

Vdload动载荷子程序实现膛内火药燃气压力动态加载的主要步骤如下：

步骤1子程序在主程序当前增量步结束时读取活塞运动位移量u(t)和火药燃气压力值P(t)；

步骤2以发射筒内表面所有积分点为预定义加载位置，子程序自动获取其轴向坐标x；

步骤4返回主程序，继续计算下一个增量步；

步骤5步骤1～步骤4循环进行直至达到设定的分析步时间，Vdload动载荷子程序工作流程示意图,如图5所示。

图4 膛压曲线Fig.4 The characteristic curve of bore pressure

3 发射过程仿真结果分析

3.1 动态发射过程仿真与试验对比

利用显示动力学求解器模拟某动能破门弹的动态发射过程，图6为仿真得到的弹丸速度和位移曲线。从图6可知，弹丸离膛速度为159.5 m/s，而试验测试值为172.0 m/s，仿真结果与试验结果之间的误差为7.3%。图7给出了击发后不同时刻弹丸与平衡体位置示意图。在4.5 ms时刻，弹丸尾部刚好离开发射筒端面，与实弹射击试验得到的弹丸离膛时间基本相同。因此，仿真得到的弹丸离膛时间及其运动参数与实弹射击试验结果相符合，验证了有限元模型的准确性。

图8显示了仿真得到的变形环塑性变形与实弹射击试验后变形环塑性变形结果对比。发射过程中，活塞在火药燃气压力作用下推动弹丸和平衡体向两侧运动，当活塞端面与变形环端面接触后，活塞会挤压变形环使其发生塑性变形吸能，从而减少复合材料筒体的轴向受力。有限元仿真得到的变形环塑性变形与弹丸发射后的真实塑性变形结果基本一致，进一步验证了所建立的非线性弹-管耦合动力学模型的准确性。

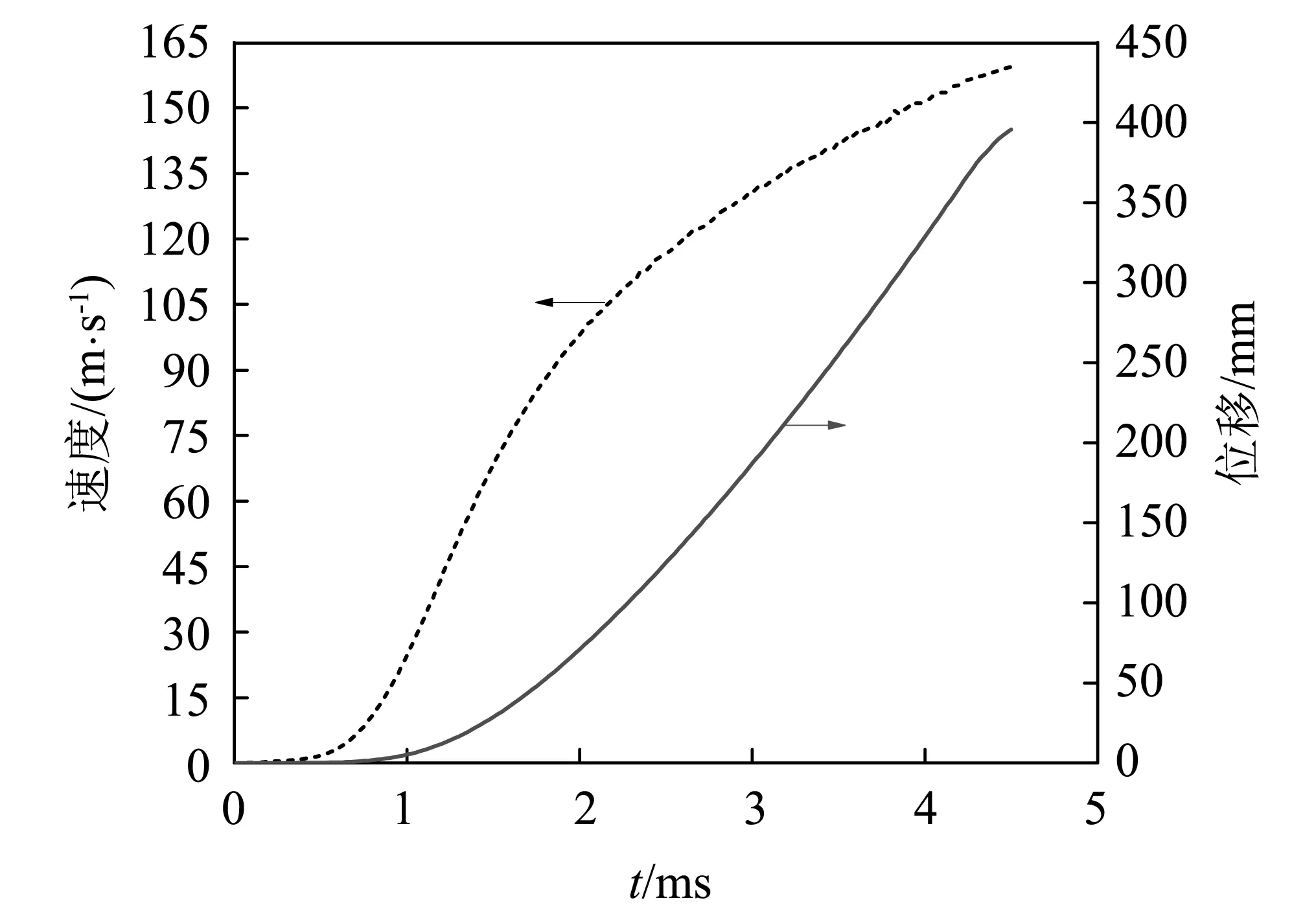
图6 弹丸速度和位移曲线Fig.6 Velocity and displacement curves of projectile

图7 弹丸、平衡体位置动态变化过程示意图Fig.7 Schematic diagram of dynamic positionof projectile and balance body

图8 塑性变形结果对比Fig.8 Comparison of plastic deformation

3.2 复合材料发射筒动态强度分析

复合材料发射筒由高强玻纤S4C9-960/环氧-酸酐树脂体系和T700/环氧-酸酐树脂体系两种材料交替缠绕后经固化、机加工而成。其中，碳纤维主要为环向缠绕，并且在筒体高压段(中部)用碳纤维进行连续7层的环向缠绕，以保证筒体能够承受瞬时高压火药燃气的动态冲击作用。高强玻璃纤维为纵向±23.5°缠绕，主要用于承受轴向制动力作用。因此，本文分别提取了环向缠绕层与纵向缠绕层在击发后不同时刻的应力分布云图，分析复合材料发射筒的动态强度。

图9为发射过程中复合材料发射筒环向缠绕层(第20层)的动态Von Mises应力分布云图。可以明显看出，应力较大部位主要位于两侧活塞所围成的区域，且发射筒受载面积随弹丸和平衡体的运动而发生动态变化，与实际发射工况一致，即实现了火药燃气压力二维瞬态分布与弹丸运动相互关联的动力学过程，真实地模拟了复合材料发射筒受到的强动态冲击效应。此外，随着复合材料受载面积的逐渐增加，复合材料筒体内的最大应力值逐渐降低，与图4所示的膛压随活塞位移量变化规律相一致。

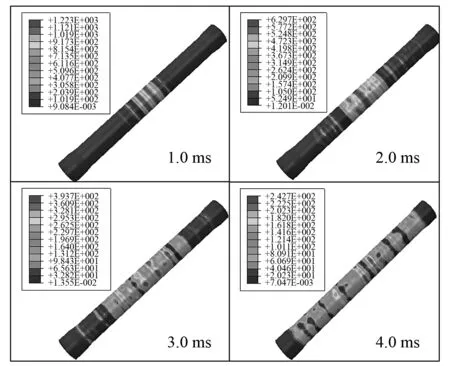
图9 第20层动态Von Mises应力云图Fig.9 Von Mises stress distribution of layer 20

由于弹丸在筒体内运动时间很短，整个发射过程存在明显的动态冲击效应，因而图9中复合材料筒体的应力云图呈现一定的应力波效应。为了直观看出筒体内的应力波动情况，提取了第20层不同时刻沿轴线方向的应力分布，如图10所示。从图10可知，复合材料筒体内的应力波动现象非常明显，并且呈现对称分布特征。另外，分别将1 ms，2 ms，3 ms和4 ms时刻的火药燃气压力作为静载施加到筒体内表面相应位置上，发现静态应力均小于图10中相应时刻的应力峰值。因此，在有可能产生应力波的强动态冲击载荷作用下，应按照应力波峰值应力来校核结构强度。

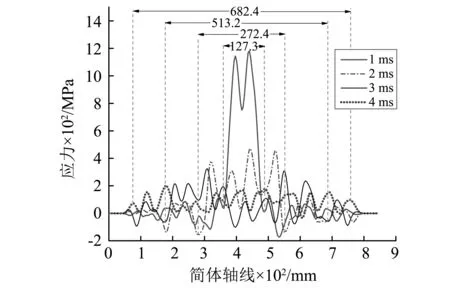
图10 第20层不同时刻沿轴线方向应力分布Fig.10 Stress distribution along the axis at different times in layer 20

图11为发射过程中复合材料发射筒纵向缠绕层的动态Von Mises应力分布云图。从图11可知，纵向(第2层)铺层内的应力呈现出现先减小后增大再减小的变化规律。在活塞与变形环接触之前，纵向铺层的应力主要是由火药燃气压力与弹-管接触碰撞力耦合作用引起的，因此纵向铺层的应力随着膛压的减小而逐渐减小；当活塞与变形环接触后，复合材料筒体内产生较大的轴向制动力，并且主要由纵向层承受制动力作用，因此纵向铺层内的应力在短时间内迅速升高，然后逐渐下降。

图11 第2层动态Von Mises应力云图Fig.11 Von Mises stress distribution of layer 2

对于纤维增强树脂基复合材料结构来说，分析沿纤维方向与垂直于纤维方向的应力分布更有助于评估结构的服役安全性。分别提取了弹丸发射过程中各纵向与环向铺层内两个主方向的最大应力值，如图12所示。从图12可知，各环向铺层内纤维方向的最大应力值基本一致，其中第20层在发射过程中的应力值最大，最大值为1 394 MPa，约为T700/环氧-酸酐树脂材料纵向极限拉伸强度的48.4%；各纵向铺层内纤维方向的应力最大值沿筒体径向逐渐减小，最大应力值为220.5 MPa，约为高强玻纤S4C9-960/环氧-酸酐树脂材料极限拉伸强度的43.8%，因此各铺层内纤维方向的最大应力都小于相应材料的极限拉伸强度，安全系数均在2.0以上。

图12 发射过程中各铺层主方向的应力最大值Fig.12 The maximum stress in the main direction of each layer during launch

各铺层内垂直于纤维方向的应力值基本不发生变化，并且纵向层内的应力大于环向层，这是由于纵向铺层的纤维方向与筒体轴线的夹角为23.5°，制动载荷引起的轴向应力在垂于纤维方向上产生了较大的应力分量。各铺层内垂直于纤维方向的最大应力小于相应材料的横向极限拉伸强度，在发射过程中不会出现损伤。总体来说，在弹丸发射过程中，火药燃气压力载荷主要由环向缠绕层承受，而活塞制动引起的轴向制动力主要由纵向缠绕层承受，在高压火药燃气的强动态冲击与弹-管接触碰撞耦合作用下，玻-碳混杂纤维缠绕复合材料发射筒处于安全状态。