基于固有频率的风力机叶片裂纹精确定位与程度识别
2019-12-31吴琪强郭帅平李学军
吴琪强, 郭帅平, 王 钢, 李学军
(湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201)
近年来,随着全球生态环境面临越来越严重的破坏,各国开始大力提倡使用风能这种绿色清洁能源,目前中国已经成为全球风电装机容量最大的国家,预计到2020年全国风电装机容量将达到100 GW[1-2]。
随着风电产业的不断发展,风力发电机组的故障问题也将随之而来;截止到2019年3月31日,根据Caithness Windfarm Information Forum[3]提供的事故统计数据表明,由风电机组故障而引发的事故总数共2 475起。在众多事故中,由风力机叶片故障引起的事故数量最多,共415起,其中叶片裂纹损伤引起的事故后果最严重。风力机叶片是风力发电机组的关键部件且价格昂贵,成本可以占到风力发电机组装机成本的15%~20%[4]。叶片在运行过程中所处环境恶劣且工况复杂,由于长时间受到循环载荷的作用,导致材料退化和疲劳而萌发裂纹;若不及时修复,裂纹会迅速扩展而产生旋转不平衡,从而可能引起整个塔架的倒塌,造成重大安全事故[5]。同时,风力机叶片的裂纹维修需要大量的停机时间[6]。因此,为了保证风力发电机组长时间安全运行,降低停机损失及大事故重大损失,定期监测和持续评估风力机叶片的结构健康状况具有重要意义[7]。
在过去的几十年中,国内外学者相继研究了多种无损检测方法运用于结构损伤检测,如光纤、声发射、超声波、X射线和热成像等[8-11],它们能够对叶片进行内部损伤检测、长距离检测、分层检测、孔隙检测等,但是在检测过程中需要近裂纹位置附近,且对于叶片裂纹的精确诊断和定性分析具有一定的难度。基于叶片振动响应的损伤识别方法能够节约时间和降低成本,且无需靠近裂纹位置附近的区域[12]。张宇飞等[13]提出了基于频响函数虚部的梁结构损伤检测方法,能检测出损伤的位置,并且能定性的表征损伤的程度。裂纹的产生将引起叶片结构发生改变,从而导致结构模态参数发生变化,故叶片模态参数的改变可视为诊断裂纹产生的依据。
模态参数是结构物理特性,一般包括固有频率、模态振型和模态阻尼。当叶片出现裂纹时,会导致结构模态参数发生变化。很多学者利用模态振型差值曲率来识别风力机叶片等结构的裂纹位置,并通过试验验证了方法的有效性,虽然该方法能够在一定程度上能很好的检测出损伤的程度和位置[14-17]。考虑在实际运用中,由于裂纹引起叶片的模态振型差值曲率较小(10-4),以及测试结构自由度不足和测试噪声等影响,导致模态振型的测量存在较大的误差,损伤识别结果可靠性较低。
基于固有频率参数检测结构损伤已经广泛应用于多种实际结构中,在低阻尼结构中频率测试分辨率达到0.1%,甚至更高[18];同时,结构固有频率测量简单、误差较小,并且可以在结构的运行过程中多次测量,适用于在线监测[19]。大多数学者通过测量或计算结构的固有频率变化,确定结构是否存在损伤以及损伤位置。Cawley等[20]提出了用频率变化比来识别损伤的方法,并在理论上证明了当一个结构有损伤时,任意两阶固有频率变化之比,只与损伤的位置有关而与损伤的程度无关; 金虎等[21]提出了一种基于神经网络的桁架裂纹诊断方法,该方法能够定位裂纹所在的部件,也能识别损伤程度,但是对于裂纹位置以及损伤程度识别的精度较低,难以满足实际应用。Zhang等[22]提出一种高精度的悬臂梁固有频率采集方法,可以描述变截面悬臂梁的固有频率变化率及其裂纹特征;Yu等[23]基于风扇叶片的离散数学模型,利用固有频率的变化结合流体结构分析,开发了一种简单的方法来检测损伤。
通过上述分析发现,大多数学者基于振动响应的结构裂纹诊断方法难以精确识别裂纹特征,在裂纹定位过程中,存在只能确定损伤存在的单元位置等定位精度不高的问题,进而导致损伤程度的可靠性更低。
为了能够更加精确的诊断叶片裂纹特征,本文利用固有频率作为叶片裂纹诊断参数。考虑横向裂纹对于结构特性影响最大[24],本文主要研究叶片的单个横向裂纹。在叶片取多个裂纹位置,分析研究不同裂纹位置叶片与完整叶片固有频率的变化,建立叶片裂纹位置参数数据库。通过本文提出的裂纹定位参数和裂纹区间定位方法,实现裂纹所属区间定位。研究区间内不同裂纹位置与定位参数之间的关系,精确定位裂纹位置。研究裂纹损伤程度与裂纹位置之间的映射关系,针对风力机叶片不同裂纹位置建立了裂纹损伤程度函数模型,当叶片裂纹位置确定时,叶片裂纹程度可精确识别。最后通过试验验证了该方法对结构裂纹诊断的有效性,同时能够实现裂纹的在线监测。
1 基本原理
1.1 裂纹叶片模态特性分析
本文研究叶片结构损伤对固有频率的影响,忽略环境和阻尼的影响,则结构的振动方程为[25]
(K-ω2M)φ=0
(1)
式中:K,M分别为结构整体质量矩阵、刚度矩阵;ω,φ分别为系统的固有频率和振型。当结构存在损伤时,其质量矩阵和刚度矩阵将发生改变,ω,φ也随之改变,则结构的振动特征值方程为
[(K-ΔK)-(ω2-Δω2)M](φ-Δφ)=0
(2)
整理得
(3)
则第i阶固有频率变化量的平方为
(4)
为了得到单元损伤与整体振动响应变化之间的关系,将整体刚度K分解为各构件刚度矩阵kN,将固有振型φ计算由单个构件N变形εN(φ)所得
(5)
式中:εN为单元变形向量。当结构存在单损伤时,损伤位置在N,则
(6)
式中:N为损伤单元号;ΔkN为单元刚度变化量。定义单元损伤系数αN
Δk=αNkN
(7)
式中:kN为初始单元刚度矩阵。
整理得第i阶固有频率变化量的平方
(8)
同理,可得到第j阶固有频率变化量的平方,两式相比
(9)
在单裂纹损伤情况下,由式(9)计算,等式右边与左边相等时,则损伤发生在该单元。即结构任意两阶固有频率的变化之比或变化平方比,只与损伤位置有关,与损伤程度无关。当风力机叶片同一位置出现损伤,可通过获取损伤叶片任意两阶固有频率变化之比或变化的平方比来识别损伤位置。
1.2 叶片裂纹定位参数
基于上述分析可知,大多数学者通过固有频率参数只能确定待测叶片裂纹所属的单元,但在实际叶片中位置难以精确定位,为了精确定位叶片裂纹位置,本文提出叶片裂纹定位参数,在单裂纹叶片中,记裂纹与叶根距离为
Lc(n)=Δd·n(n=1,2,…,NM)
(10)
式中:n为叶片裂纹位置序号;NM为叶片裂纹位置个数;Δd为叶片相邻两个裂纹之间的距离。
(11)
基于裂纹引起的叶片任意两阶固有频率变化之比只与损伤位置有关的性质, 建立单裂纹位置参数Hn
(12)
由裂纹叶片固有频率特性可知,参数Hn的取值将与裂纹位置Lc(n)一一对应。针对同型号风力机叶片,同位置不同程度的损伤对应位置参数Hn的差值等于0或者趋近于0。基于式(12)可知,通过裂纹位置参数Hn可识别裂纹位置;所以,可通过试验或者仿真分析,分别在Lc(n)预设裂纹,基于试验或仿真结果,通过计算不同裂纹位置叶片的相邻两阶固有频率的变化之比,建立裂纹位置参数Hn数据库,为裂纹定位提供数据支持。
2 叶片裂纹高精度定位方法
基于“1”节分析,本节将介绍一种基于裂纹位置参数Hn的高精度裂纹定位方法。首先在叶片上选择有限个截面,分别在这些截面植入缺口型裂纹,如图1所示,获得基于参数Hn的数据库,这些截面也将叶片划分为多段区域,通过得到的数据库和本文提出的定位方法,实现裂纹所在区间的定位;其次通过研究裂纹在区间内的位置与裂纹参数的关系,实现裂纹在区间内位置的准确定位。本节提出的叶片裂纹高精度定位方法也为后续叶片损伤程度的识别提供必要基础。
2.1 叶片裂纹位置参数数据库的建立
若记叶片总长为L,研究调查发现距叶根30%~35%L和70%L的位置容易萌发裂纹[26],故在建立叶片裂纹位置参数数据库时,预设裂纹位置只考虑80%L以内的位置。
本文以某型号风力机叶片为研究对象,其叶片结构及三维模型如图1所示,叶片根部长度L1=0.5 m,叶片长度为L=19 m,叶片最大宽度b=3 m,最大高度h=2 m,裂纹位置距叶片根部的距离记为Lc,裂纹深度记为d,叶片材料为玻璃纤维复合材料,其弹性模量为73 GPa,泊松比为0.23,密度为2 540 kg/m3。

图1 叶片结构示意图及三维模型Fig.1 Wind turbine blade structure diagram and 3D model
为建立单裂纹位置参数Hn,数据库中裂纹位置间隔Δd=0.5 m,裂纹位置个数NM=30,即
蒙元时期,各民族互相影响,在人们的名字方面就是如此。有的汉人受蒙古人的影响,取名具有蒙古人的习惯和色彩,赵翼《廿二史札记》卷三○:“元时汉人多有作蒙古名者。”反之,有的蒙古人或其他民族受汉人的影响,也取汉人的姓名。在游牧文化中,牲畜并不低贱,这与汉文化恰恰相反,他们常常以牲畜或动物作为名字,以寄托长辈的某种期许。钱大昕《十驾斋养新录·蒙古语》:
Lc(n)= 0.5n(n=1,2,…,30)
(13)
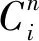
2.2 叶片裂纹区间定位方法
记待诊断叶片的裂纹位置为距叶根x处,定义裂纹定位参数Pn,x
(14)

表1 部分叶片裂纹位置固有频率差值比数据库

本文提出裂纹区间定位准则如下:
(1) 针对x处存在损伤的叶片,基于数据库,计算风力机叶片损伤定位参数Pn,x,得到Pn,x最小值对应的裂纹位置r,则未知裂纹位置在位置r临近区间,即
r,Pr,x=min{P1,x,P2,x,…,PNM,x}
(15)
(2)基于位置r,比较Pr-1,x与Pr+1,x,得到最小值对应的裂纹位置t,即
(16)
由式(15)、式 (16)可确定裂纹位于位置r和位置t的区间内,且更靠近r一侧;Pr-1,x与Pr+1,x差值越小,裂纹越靠近位置r。
基于上述裂纹定位参数和区间定位方法,可实现裂纹所在区间的定位。
2.3 叶片裂纹区间内精确定位方法
风力机叶片型号种类多,建立所有叶型叶片完整的裂纹位置参数数据库难以实现;同时,数据库中裂纹区间长度设置太小会使实际裂纹叶片固有频率测量产生较大误差,从而导致区间定位的准确性下降,故在实际建立的叶片裂纹位置数据库时,设置的裂纹位置间隔不宜太小。同时,叶片裂纹损伤程度识别的准确性是由裂纹定位的精度来决定,通过“2.2”节叶片裂纹区间定位方法可以确定裂纹所属区间,若无法进一步确定裂纹在区间中的精确位置,将会影响叶片裂纹损伤程度识别的准确性。所以,需要基于上述叶片裂纹区间定位方法,进一步研究在裂纹所在区间内的精确定位,实现精确定位裂纹位置。
本文建立的数据库中,叶片裂纹位置间隔0.5 m,基于“2.2”节裂纹区间定位方法,假设裂纹定位于区间[r,r+1]内,令单裂纹在区间内移动,研究裂纹定位参数Pr,x与Pr+1,x随裂纹位置变化的规律,并将由Pr,x与Pr+1,x拟合的曲线分别记为Pr(x)与P′r(x);考虑所有区间,其中部分区间拟合曲线如图2所示。
由图2可知,各区间的拟合曲线Pr(x)与P′r(x)趋势一致,但各曲线重合度不高;为取得各区间Pr,x与Pr+1,x随裂纹位置变化的共性特征,本文将Pr(x)与P′r(x)作比值,即

图2 [r ,r+1]内裂纹位置与裂纹定位参数之间的关系Fig.2 Relationship between crack location and crack location parameters in [r ,r+1] region
(17)
由式(17)得到一条新的曲线Er(x),将区间[r,r+1]转化为[0,1]参数空间,各区间的Er曲线在参数空间的形状如图3(a)虚线所示,各曲线十分贴近,几乎重合,即Er参数为各区间裂纹位置的共性特征。图3(b)为图3(a)中黑方框的局部放大图,其中,最外侧两条曲线的位置最大误差仅为0.012 5。

(a)比值曲线整体图

(b)比值曲线局部图图3 各曲线作比值图Fig.3 Curve ratio diagram
将各Er(x)曲线拟合成一条曲线Er(ζ),其中,ζ为裂纹相对位置如图3粗实线所示,其表达式为
(18)
观察图3中曲线Er(ζ)可知,曲线Er(ζ)关于ζ=0.5对称,且Er(0.5)=1时,Pr与P′r的取值相等,即裂纹位于区间中点。
将得到的曲线Er(ζ)作为裂纹区间内精确定位的判断依据,即建立了裂纹位置x与函数Er(ζ)的一一对应关系。针对区间[r,r+1],基于式(18)可得到以下裂纹相对位置ζ的函数
(19)
根据区间[r,r+1]与参数空间的映射关系,得到裂纹在区间[r,r+1]的更准确的位置
x=Lc(n)+ζ·Δd
(20)
为了更好的描述叶片裂纹定位的精度,定位如下精度计算式
(21)
式中:x为诊断出的裂纹位置;x*为裂纹实际位置。
基于式(21)可评价裂纹定位的精度。
2.4 叶片裂纹位置精确定位方法
基于上述裂纹叶片区间定位方法、区间内裂纹定位方法研究可知,对于任意型号叶片,都可实现裂纹的精确定位。所以,本文得出的针对任意叶型叶片的裂纹精确定位方法如下:
步骤1 采用试验测试或仿真分析方法,针对该叶型叶片,基于式(10)分别植入对应位置的单裂纹,得到基于式(11)式(12)的裂纹位置参数数据库;
步骤2 基于式(17),得到裂纹在区间内的位置与位置参数Er(x)的对应关系,即式(18)式(19);
步骤3 针对含单裂纹的该叶型待诊断叶片,基于实时监测得到叶片固有频率信息,基于式(11)式(12)得到该叶片的裂纹位置参数,并基于步骤1得到的数据库及式(14)~式(16),确定裂纹所在区间;
步骤4 基于式(17)计算区间内的位置参数,并基于步骤2得到的区间内位置与位置参数的函数关系,即式(19)式(20),得到裂纹的精确位置。
3 叶片裂纹损伤程度识别方法
当裂纹损伤达到一定程度后,若不采取必要的措施,很可能导致叶片发生折断,影响整机安全,导致重大事故。因此,有效地叶片裂纹损伤程度识别是避免叶片折断、导致重大事故的重要手段。
3.1 叶片损伤程度识别参数
由式(1)和式(4)可知
(22)
将式(6)、式(7)代入式(13)可得
(23)
由式(22)可知,δ同时与裂纹位置N和损伤程度Δkx相关。若能先定位裂纹的位置,则此时δ与叶片裂纹损伤程度存在一一对应的关系,可基于此对应关系进行损伤程度识别;相反,若无法准确定位裂纹,或裂纹定位误差较大,则也将影响基于参数δ的裂纹程度识别。
基于上述分析可知,针对叶片裂纹定位和裂纹程度识别,可基于裂纹位置参数Hn实现裂纹的准确定位,并以此为前提,基于参数δ实现裂纹程度识别。
3.2 裂纹损伤程度参数特性研究
本文以裂纹深度与叶片厚度的比值来定义裂纹损伤程度,即
(24)
式中:dx为叶片裂纹深度;hx为叶片裂纹所属截面的高度,下标x表示裂纹位置。通过建立裂纹损伤程度αx与损伤识别系数指标参数δ(x)之间对应关系,可实现不同损伤程度的裂纹识别。
建立不同裂纹位置Lc(n)和不同裂纹损伤程度αn的叶片有限元模型,裂纹位置根据式(13)分别取n=4,n=6,n=8,n=12,n=16,n=20,n=24,裂纹损伤程度分别取α=0,α=10%,α=20%,…,α=60%。通过数值仿真得到相应裂纹叶片的固有频率,并由式(23)计算其裂纹损伤系数指标参数δ(x)的值,为研究δ(x)与损伤程度的关系,将得到的数据绘制成图,如图4所示。

图4 损伤位置与程度关系图Fig.4 Diagram of damage location and extent
由图4可知,针对同一位置,随着裂纹损伤程度的不断增大,δ(x)近似呈幂函数增长,同时,对于相同裂纹损伤程度,位置越靠近叶片根部,δ(x)值越大。根据图4中图标表示的变化规律,将基于如下函数对其进行拟合
δ(x)=px(0.1αx)qx
(25)
式中:px拟合的幂函数系数;qx拟合的幂函数指数。
通过上述函数拟合,得到了δ(x)与αx的关系,其中幂函数系数px与幂指数qx与损伤位置有关。针对上述裂纹所设置的7个位置,共得到7组对应的px与qx的取值。
为了实现连续位置处的裂纹损伤程度的识别,需要进一步研究裂纹位置x与px,qx之间的关系。
分别研究上述7组px,qx与裂纹位置x之间的函数关系,将px,qx随裂纹位置x的变化关系绘制成图,如图5、图6所示,其中图5的纵坐标均采用lg比例。

图5 幂函数系数px与损伤位置图Fig.5 Power function coefficient and damage location map

图6 幂函数指数qx与损伤位置图Fig.6 Power function index and damage location map
由图5、图6可知,lgpx与裂纹位置近似呈二次函数关系,指数qx与裂纹位置近似呈线性关系,其函数关系可拟合为
lgpx=-2.073 96-0.061 33x-0.008 19x2
(26)
qx=1.965 9+0.092 71x
(27)
由式(26)和式(27)可知,当叶片裂纹位置x确定时,δ(x)与αx的函数关系式(25)也将随之确定,即
(28)
式(28)可用于任意位置裂纹损伤程度的识别。为了描述叶片裂纹损伤程度识别的准确性,将损伤程度识别精度定义为
β2=1-|αx-α|
(29)
式中:αx为诊断出的裂纹损伤程度;α为裂纹实际损伤程度,基于式(28)式(29)可得出叶片裂纹损伤程度识别的准确程度。
3.3 叶片裂纹损伤程度识别方法
基于上述裂纹叶片损伤程度系数参数特性研究可知,对于任意型号叶片,通过“2”节叶片裂纹高精度定位方法实现裂纹的精确定位后,进而可进行裂纹损伤程度的精确识别。故本文得出的针对任意叶型叶片的裂纹损伤程度识别方法如下:
步骤1采用试验测试或仿真分析方法,针对该叶型叶片,基于式(10)式(24)分别植入对应位置和损伤程度的单裂纹,得到基于式(23)的不同裂纹位置和损伤程度下损伤程度系数参数δ;
步骤2基于参数δ,得到不同位置下δ与裂纹损伤程度对应的函数关系,即式(25),以及得到裂纹位置与式(25)中的参数之间的函数关系式,即式(26)式(27) ;
步骤3基于“2”节得到的裂纹精确位置x和式(26)式(27),得到该裂纹位置叶片损伤程度函数关系式,即式(28);
步骤4基于实时监测得到叶片固有频率信息,得到基于式(23)该叶片的裂纹损伤程度系数参数δ(x),并基于步骤3得到的该裂纹叶片损伤程度函数关系式(28),精确识别裂纹损伤程度。
4 数值算例验证
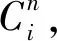

表2 裂纹位置7.3 m叶片前5阶固有频率
Hx=(0.623 0.057 0.061 0.241)T
(30)
由式(16)可知,Pn,x为数据库Hn与待测裂纹叶片裂纹位置参数Hx计算值,其结果如图7所示。
由式(15) 、式(16)计算得r=15,t=14,即叶片裂纹位置位于距离叶片根部7.0~7.5 m处且靠近7.5 m,本例预设裂纹位置x=7.3 m确实处于该区间内,说明裂纹区间定位方法有效。
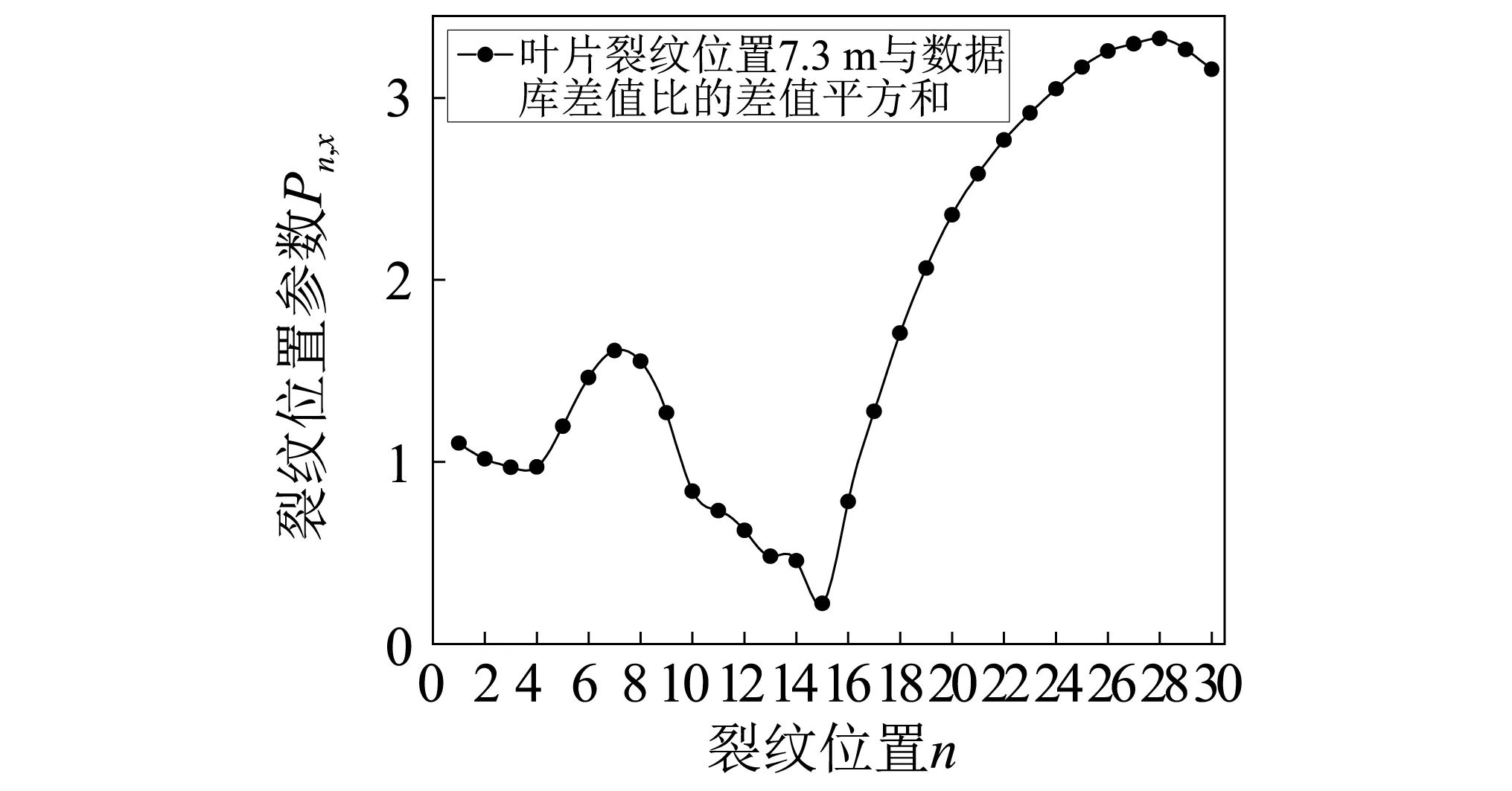
图7 叶片裂纹位置7.3 m与数据库差值比的差值平方和Fig.7 Sum of the difference between the blade crack location 7.3 m and the database difference ratio
基于上述“2.4”节裂纹精确定位方法,由式(17)可知,Er(ζ)=0.840 59,由式(19)计算得ζ=0.544 56。
根据式(20)可知,x=7.272 8 m,即确定裂纹对应的实际位置为7.272 8 m。
由式(21)可知,裂纹叶片精确定位的精度为
β1=99.86%
(31)
与设定的裂纹位置相符合,且定位精确高。
基于以上分析与验证,本文提出的裂纹区间定位及区间内精确定位方法能够精确定位裂纹位置。
上述裂纹叶片精确定位裂纹位置为x=7.272 8 m,基于“3”节裂纹损伤程度识别可知,待测叶片对应的损伤程度曲线由式(26)式(27)确定幂函数系数和指数,即
px=0.001 118 789 6
(32)
qx=2.639 123 71
(33)
由式(32) 式(33)可知,待测裂纹叶片损伤程度曲线为
δx=0.001 118 789 6(0.1αx)2.639 123 71
(34)
由表2可知待测裂纹叶片固有频率,由式(14)计算,叶片的裂纹损伤程度参数为
δx=0.087 195 567
(35)
由式(34)计算可知,则叶片的裂纹损伤程度为
αx=5.209 648×10%=52.096 48%
(36)
由式(29)可知,待测叶片裂纹损伤识别精度为
β2=99.096%
(37)
与预设的裂纹损伤程度(αx=53%)相符合,且识别精度高。基于以上分析与验证,本文提出的基于固有频率的裂纹诊断方法能够精确诊断裂纹损。
5 试验验证
5.1 试验台装置布局

试验采用B & K公司Plus测试系统测量管结构不同裂纹位置管结构固有频率,相邻两个裂纹位置间隔Δd= 160 mm,共设8个不同裂纹位置管道,4种不同损伤程度,则裂纹与管根部的距离为
(38)
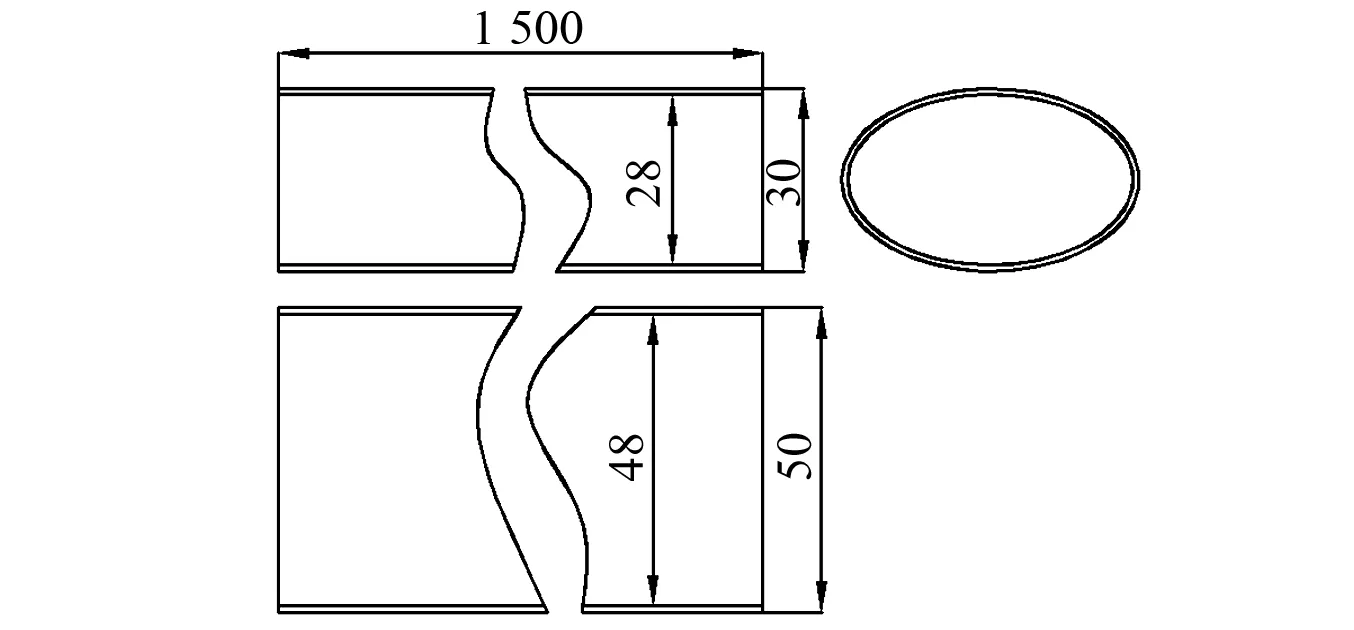
图8 管的结构示意图Fig.8 Pipe structure blade structure diagram
每个裂纹位置分别设置12种不同损伤程度,即α=5%,α=10%,…,α=60%,裂纹的形式同样为缺口裂纹。分别测试其固有频率,形成不同裂纹位置数据库。试验台装置及测试系统如图9所示。

图9 试验台装置及Brüel & Kjr测试系统Fig.9 Experimental bench unit and Brüel & Kjr test system
5.2 试验测试及分析
将待测裂纹管假想等份20个点,依次敲击20个点,通过传感器直接测量出无裂纹和不同位置裂纹的空心管每点对应的频率响应函数曲线,对每一个点的敲击都采用5次平均处理,保证其准确性。
通过多次测量,取无裂纹管和不同裂纹位置管的前5阶固有频率,形成裂纹位置数据库,表3所示以损伤程度为10%为例。


表3 部分管结构裂纹位置固有频率差值比数据库
同样将其转化在[0,1]参数空间内;同时,由式(18)得到拟合Er曲线,如图10虚线所示。
将两条拟合的Er曲线拟合成一条曲线Er(ζ),如图10实线所示,其表达式为
(39)
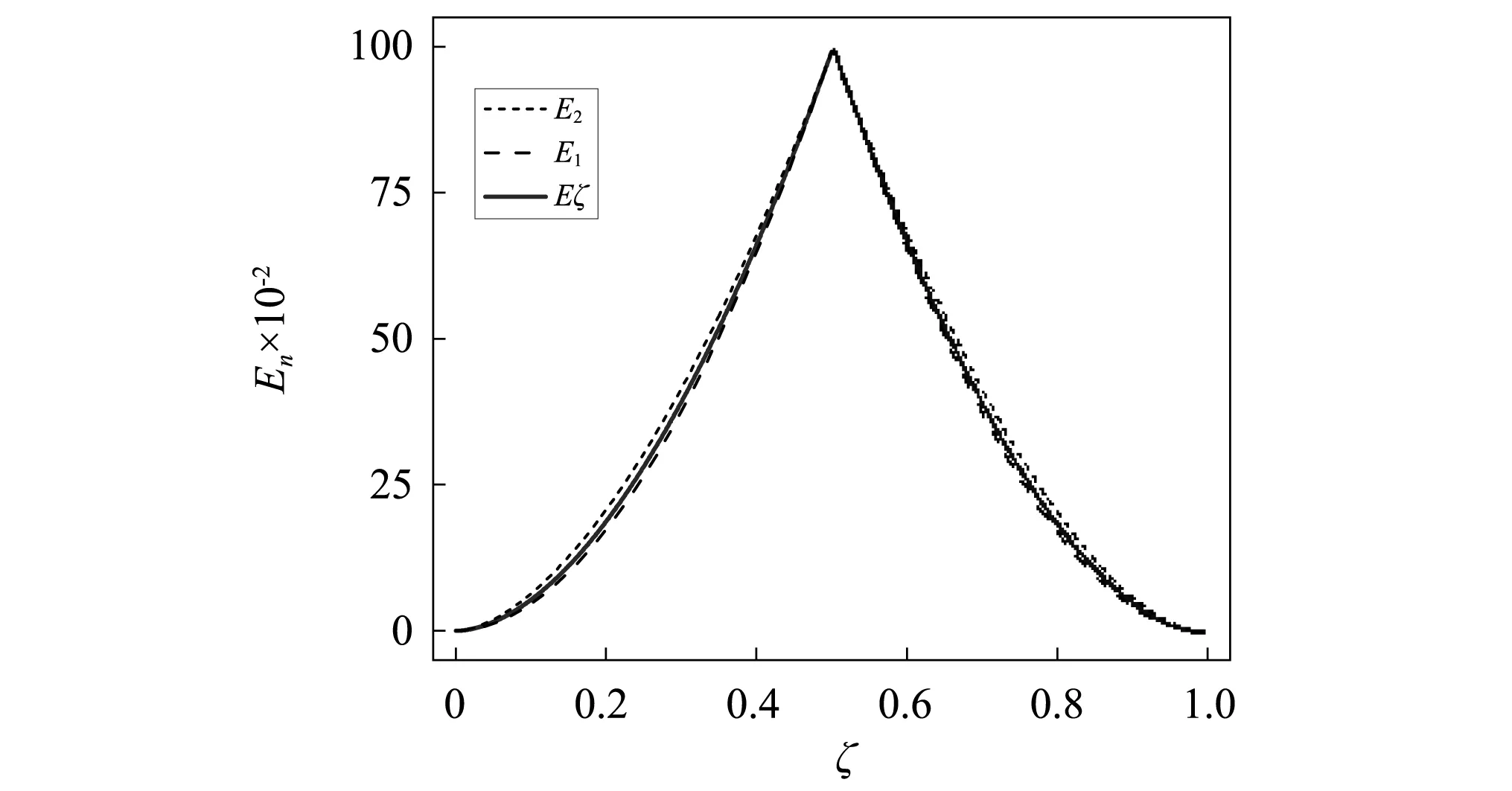
图10 各曲线作比值图Fig.10 Curve ratio diagram
由式(39)可知,裂纹的相对位置ζ表达式为
(40)
基于“3.2”节叶片裂纹损伤程度识别方法和试验设置的12种不同损伤程度的裂纹,分别计算其损伤程度系数参数,并将得到的δ分段拟合曲线,如图11所示。
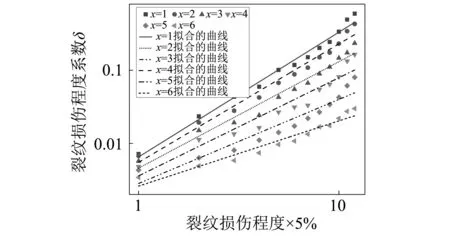
图11 损伤位置与程度关系图Fig.11 Diagram of damage location and extent
通过图11可知,随着裂纹损伤程度的不断增大,损伤指标对数与损伤程度对数近似呈线性增长,记为
lgδ(x)=px+qxlg(αx/0.05)
(41)
通过计算分析,得到不同裂纹位置拟合的截距px和系数qx与裂纹位置之间的函数关系,拟合函数关系分别如图12、图13所示。其函数关系表达式分别为
lgpx= -2.156 52-0.014 12x-0.016 69x2
(42)
qx=1.862 95-0.131 84x
(43)

图12 截距px与损伤位置图Fig.12 px and damage location map
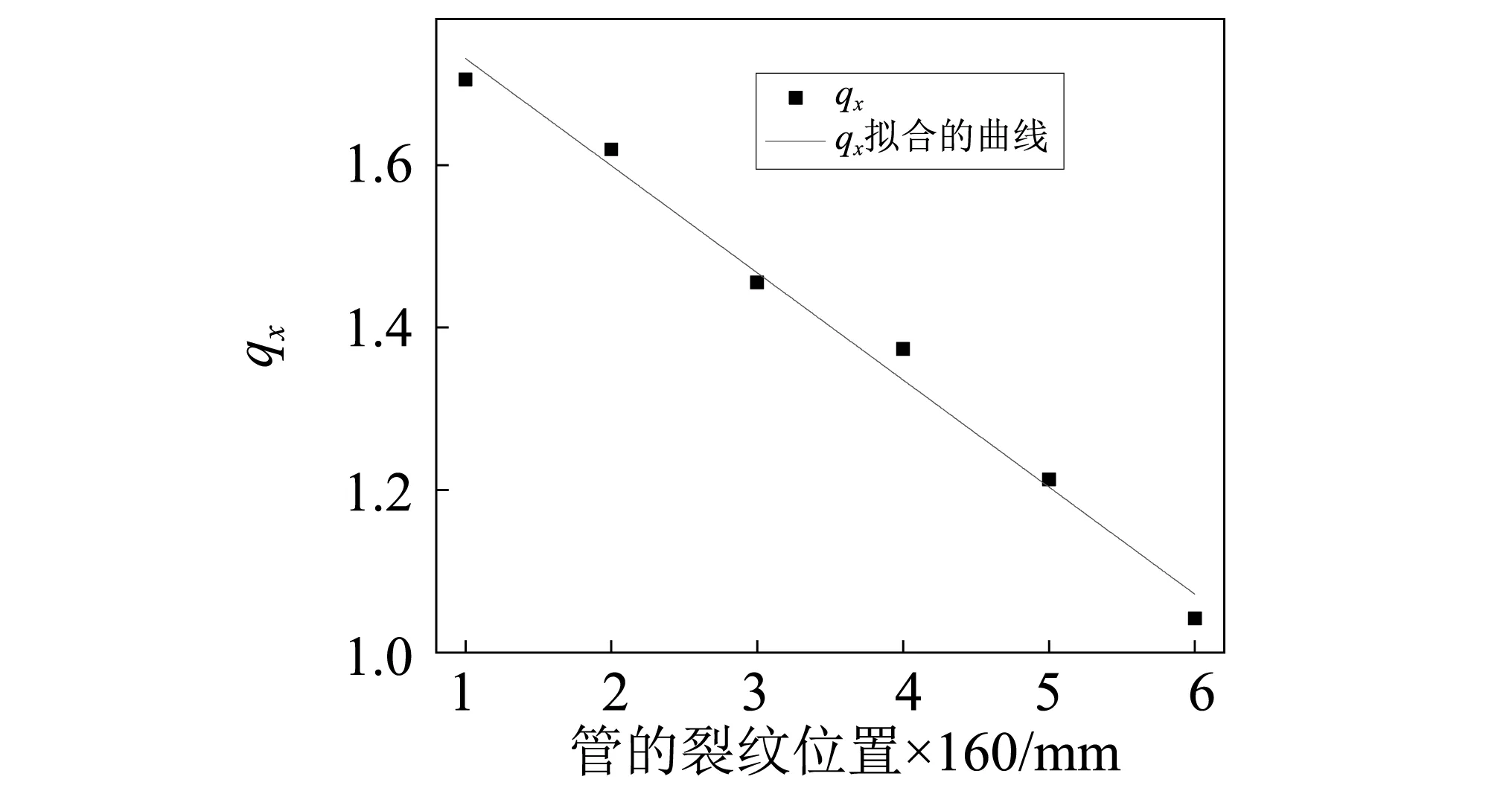
图13 系数qx与损伤位置图Fig.13 qx and damage location map
同样,由式(42) 、式(43)可知,当试验确定管道裂纹位置,裂纹损伤程度函数也将随之确定。
5.3 试验算例验证
基于本文“2~3”节裂纹定位方法,试验以裂纹位置x*=580 mm,裂纹损伤程度为10%(即d=25 mm)为例,将管道固定在实验台上,给实验台一定的振动激励力,模拟叶片在实际工况下的振动,进而测量叶片的振动数据,如图14所示;取一段时间内的信号消噪和傅里叶变换,如取图14中的方框信号为例,结果如图15所示。
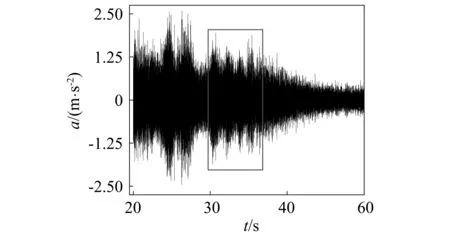
图14 管裂纹位置580 mm振动原始信号时域图Fig14 Time domain map of the original signal of the tube crack location 580 mm
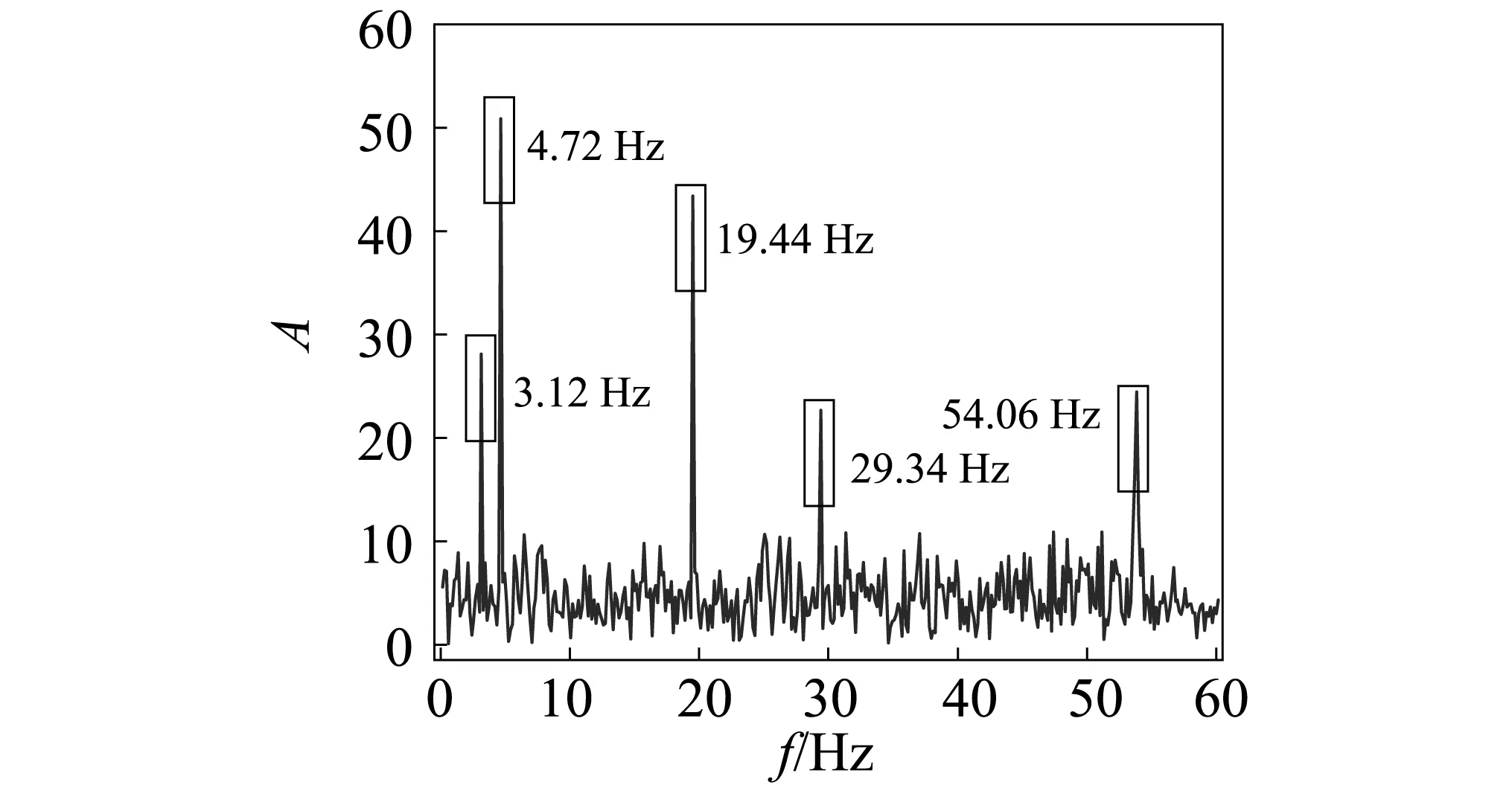
图15 稳定的时间内FFT变换结果Fig.15 FFT results of the stable operation period

表4 裂纹位置580 mm叶片前5阶固有频率及固有频率参数
Hx=(1.195 0.117 9 1.381 5 0.403 2)T
(44)
由式(16)可知,Pn,x为数据库Hn与待测裂纹叶片裂纹位置参数Hx计算值,其结果如图16所示。

图16 管裂纹位置580 mm与数据库差值比的差值平方和Fig.16 Sum of the difference between the pipe crack location 580 mm and the database difference ratio
由式(15) 、式(16)计算得r=4,t=3,即叶片裂纹位置位于距离叶片根部480~640 mm处且靠近640 mm,本例预置的裂纹位置为x=580 mm处,位于定位区间内,试验与仿真说明裂纹定位方法有效。
同样,基于上述裂纹精确定位方法,由式(17)可知,Er(ζ)=0.659 57,由式(40)、式(22)计算得,实际位置为
x=576.475 mm
(45)
由式(23)可知,裂纹叶片精确定位的精度为
β1=99.736 5%
(46)
与设定的裂纹位置相符合,且定位精确度高。
通过上述计算,确定管道裂纹位置为x=571.567 mm,基于“3”节裂纹损伤程度识别可知,待测叶片对应的损伤程度曲线由式(42)、式(43)确定幂函数系数和指数,即
px= -2.424 1
(47)
qx= 1.387 934 6
(48)
由式(47)、式(48)可知,待测裂纹叶片损伤程度曲线为
lgδ(x)= -2.424 1+1.387 934 6 (αx/0.05)
(49)
基于试验测得待测管(裂纹位置距离根部580 mm)的一阶固有频率,由式(13)计算可知,叶片的裂纹损伤程度参数为
δx= 0.010 768 149
(50)
由式(40)~式(44)计算可知,则叶片的裂纹损伤程度为
αx=2.131 6×5%= 10.658%
(51)
由式(29)可知,待测叶片裂纹损伤识别精度为
β2=99.342%
(52)
与设定的裂纹损伤程度相符合,且定位精确高。
基于上述试验验证分析可知,本文提出的裂纹损伤程度的识别方法能够精确识别裂纹损伤程度,且精度高。
6 结 论
固有频率是结构故障识别的重要参数,测量简单、精度高,且可以多次测量。本文提出了基于叶片固有频率参数的风力机叶片单个缺口裂纹诊断方法。
(1)提出了任意两阶固有频率变化比的裂纹位置参数Hn,建立裂纹位置参数数据库,提出裂纹定位参数Pn,x及裂纹定位准则,实现了叶片裂纹所属区间定位。
(2)基于叶片定位参数Pn,x在裂纹区间内的变化规律,提出符合所有裂纹区间的裂纹精确定位参数曲线En,通过计算待测裂纹叶片En,实现了叶片裂纹区间内精确定位。
(3)基于损伤程度系数参数δ只与结构的裂纹损伤程度有关,建立不同裂纹位置下,δ与裂纹损伤程度之间的函数关系;基于叶片裂纹的精确定位,确定对应的裂纹损伤程度曲线,实现叶片裂纹损伤程度识别。
(4)数值仿真和试验验证了叶片裂纹诊断方法的有效性,且精度高;本文所提出的风力机叶片裂纹诊断方法可为不同型号叶片及类似结构的裂纹提出诊断方法,为实际叶片在线检测提供理论支持。
