三跨变高度连续梁桥的精确损伤识别
2019-12-31李春良林志豪王方彦郝达靖
李春良,林志豪,王方彦,郝达靖
(吉林建筑大学 交通科学与工程学院,吉林 长春 130118)
桥梁损伤识别常用的方法有动态法和静态法。动态识别法多是基于频率、振型、模态曲率、频响参数等[1-5]开展的损伤识别,但这些动态识别法大多在数据采集过程中都对外界环境(如温度、风速、铁路等干扰)、传感器精度等要求较高。
静态识别法多是基于一些损伤识别指标来识别出结构的部分损伤信息[6-8],如基于跨中位移差值指标对简支梁的损伤识别[9]和基于竖向支座反力差值指标对两跨等刚度连续梁桥进行的损伤识别[10],还有是依靠局部抗弯刚度的变化来进行损伤识别[11]。但这些方法都是针对一跨、两跨的等高度梁结构,对变高度的结构涉及不多,而在实际工程中三跨变高度的连续梁居多。
目前也有学者基于振型模态测量建立了损伤识别指标[12],但该方法仅用于抗弯刚度连续变化的梁结构。还有一些基于统计分析[13]或模糊逻辑[14]的损伤识别方法,但研究机理尚不明确。
可见,如果能够给出一套既具有理论支持,操作性又强的损伤识别方法是十分必要的。本文结合损伤前、后变高度连续梁桥局部刚度变化的特点,基于傅里叶级数理论和数值积分法,解决了变高度连续梁桥局部损伤后刚度具有突变性和离散性在解析计算中不好处理的难题。同时,建立了变高度连续梁桥的损伤识别模型,给出了三跨变高度连续梁桥的损伤识别方法和具体的加载流程。在实际桥梁检测中,只要获得中支座反力二次差值数据,就能识别出三跨变高度连续梁的具体损伤位置、损伤范围等信息。
1 加载流程与作用位置
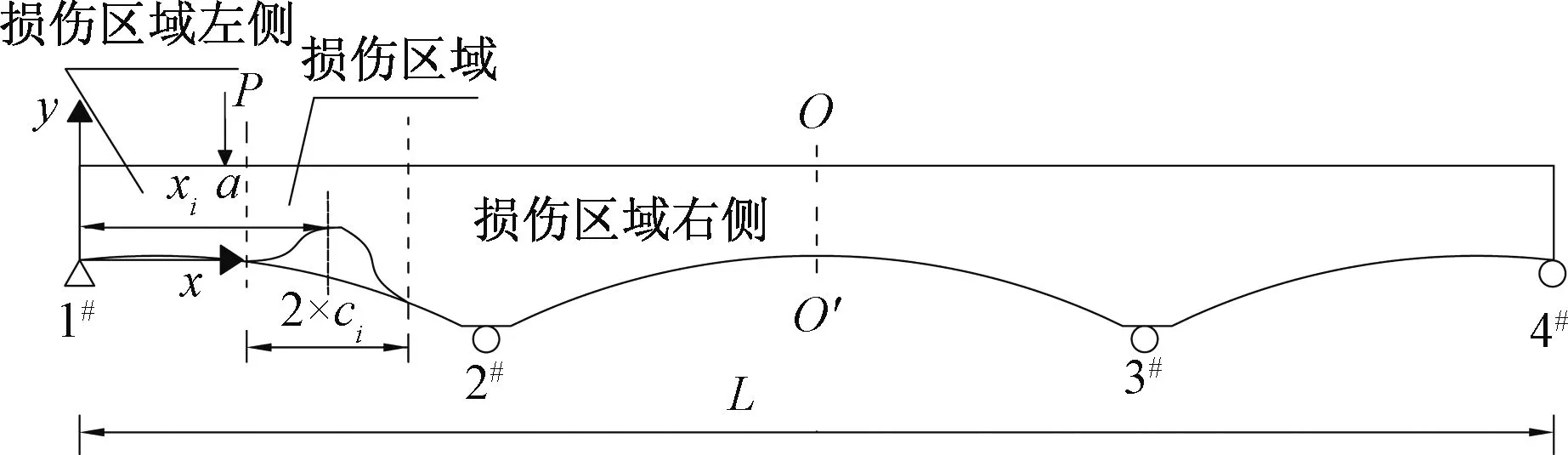
将无损伤的空间连续梁结构简化为二维梁结构,并且三跨连续梁结构在尺寸上与中跨跨中O-O′截面完全对称,见图1。
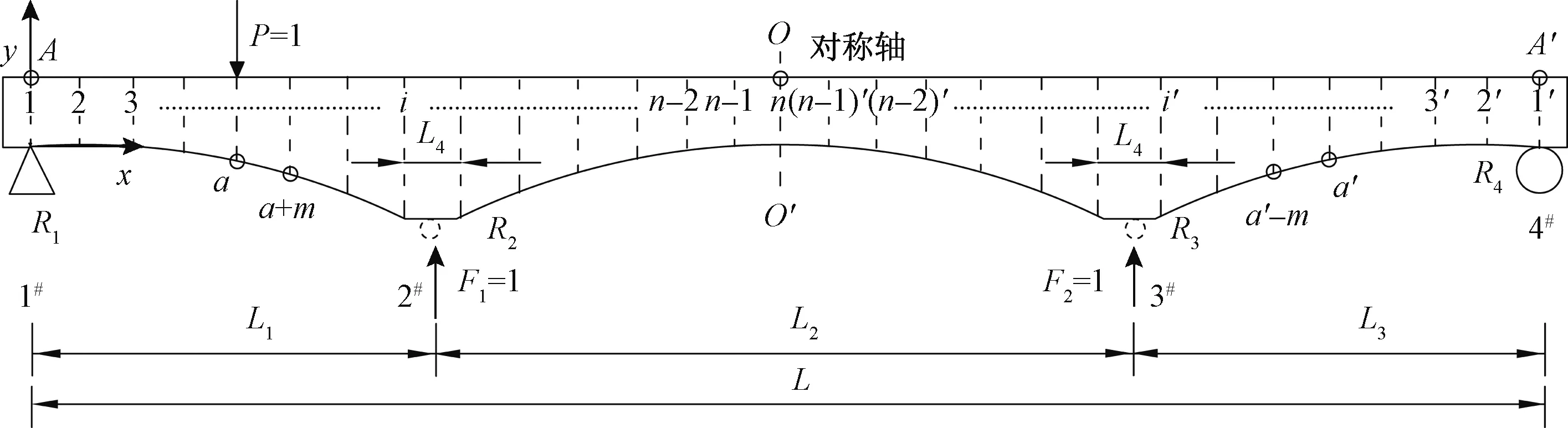
图1 三跨连续梁图与荷载作用位置
根据梁长和中跨跨中截面位置,将图1中的梁对称于O-O′轴进行等距分段,每段长度均为m。在图1中,1、2、…、n-1、n、(n-1)′、…、2′、1′点处为移动荷载F的依次作用位置。图1中a和a′、a+m和a′-m关于O-O′轴对称,a、a′为移动变量。
对图1中的结构进行检测时,主要包括正向(A-O)加载流程与反向(A′-O)加载流程。正向(A-O)加载流程指荷载F依次作用到1、2、…、n-1、n等各标记节线处。反向(A′-O)加载流程指荷载依次作用到1′、2′、…、(n-1)′、n等各标记节线处。可见,对应的正向依次加载第i位置与反向依次加载第i′位置完全对称于轴O-O′。
2 无损伤时中支座反力二次差值方程
2.1 变高度连续梁抗弯刚度整体化模型
大多数连续梁的高度都是变化的或具有多区段性。基于傅里叶理论,将变高度连续梁多区段分布的抗弯刚度表示成整体化的级数形式为[15]
(1)
式中:I(x)为结构任意x处抗弯惯性矩,可根据任意x处的截面尺寸,利用三角分块法求解出值;E为基本结构弹性模量。故用式(1)可以计算出变高度连续梁在任意x处的抗弯刚度值,方便数值积分直接使用。
2.2 无损伤时中支座反力基本方程
将图1中的连续梁结构的中间支座去掉,变成静定的基本结构,并添加未知力F1、F2等效。当荷载P移动到a处时,能建立未知力的表达式为
(2)
(3)
式中:F1、F2分别为2#、3#支座处添加的未知力。整理得出式(2)、式(3)中的各系数表达式为
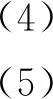
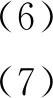

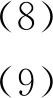
(10)

(11)
(12)


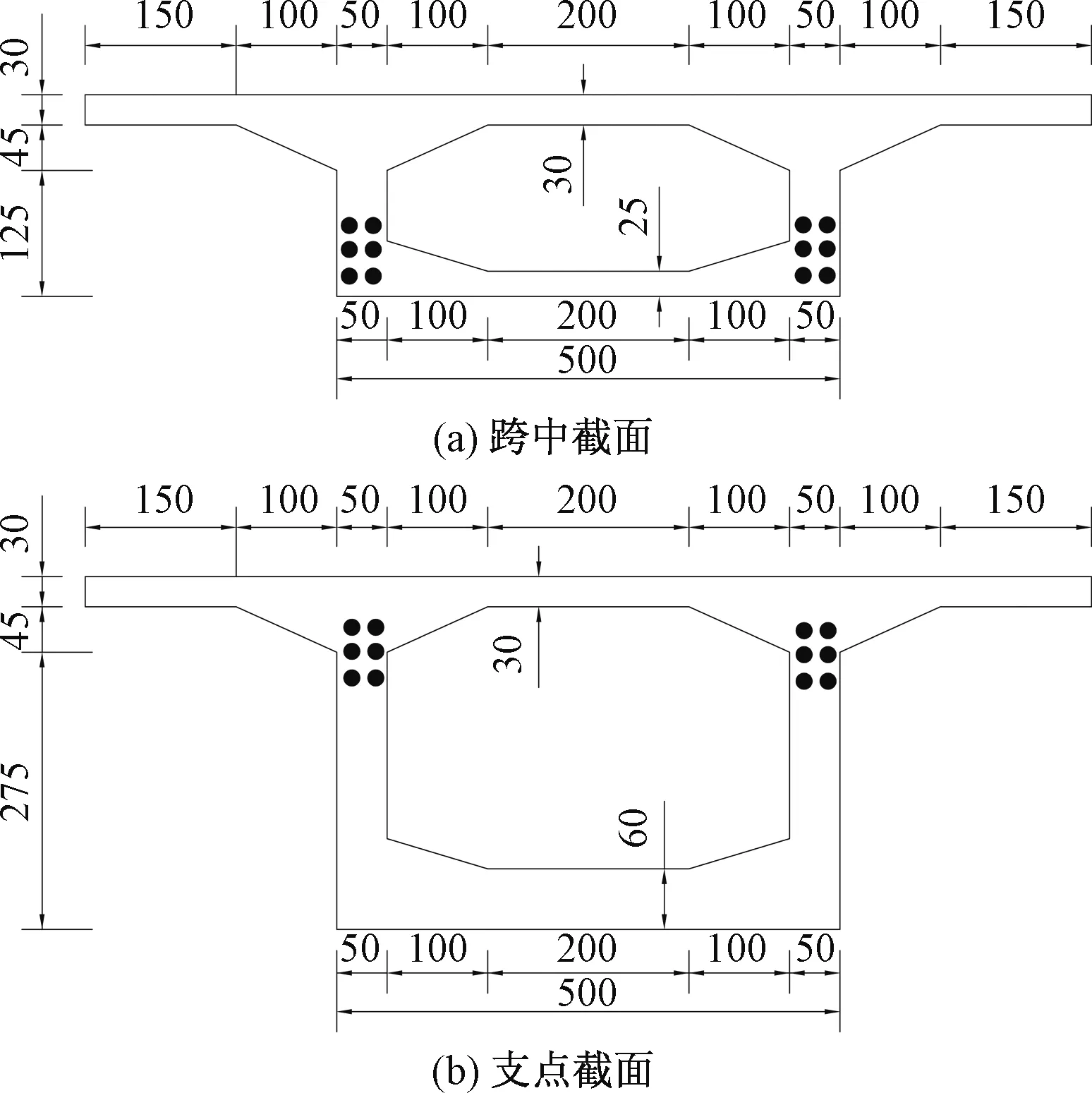
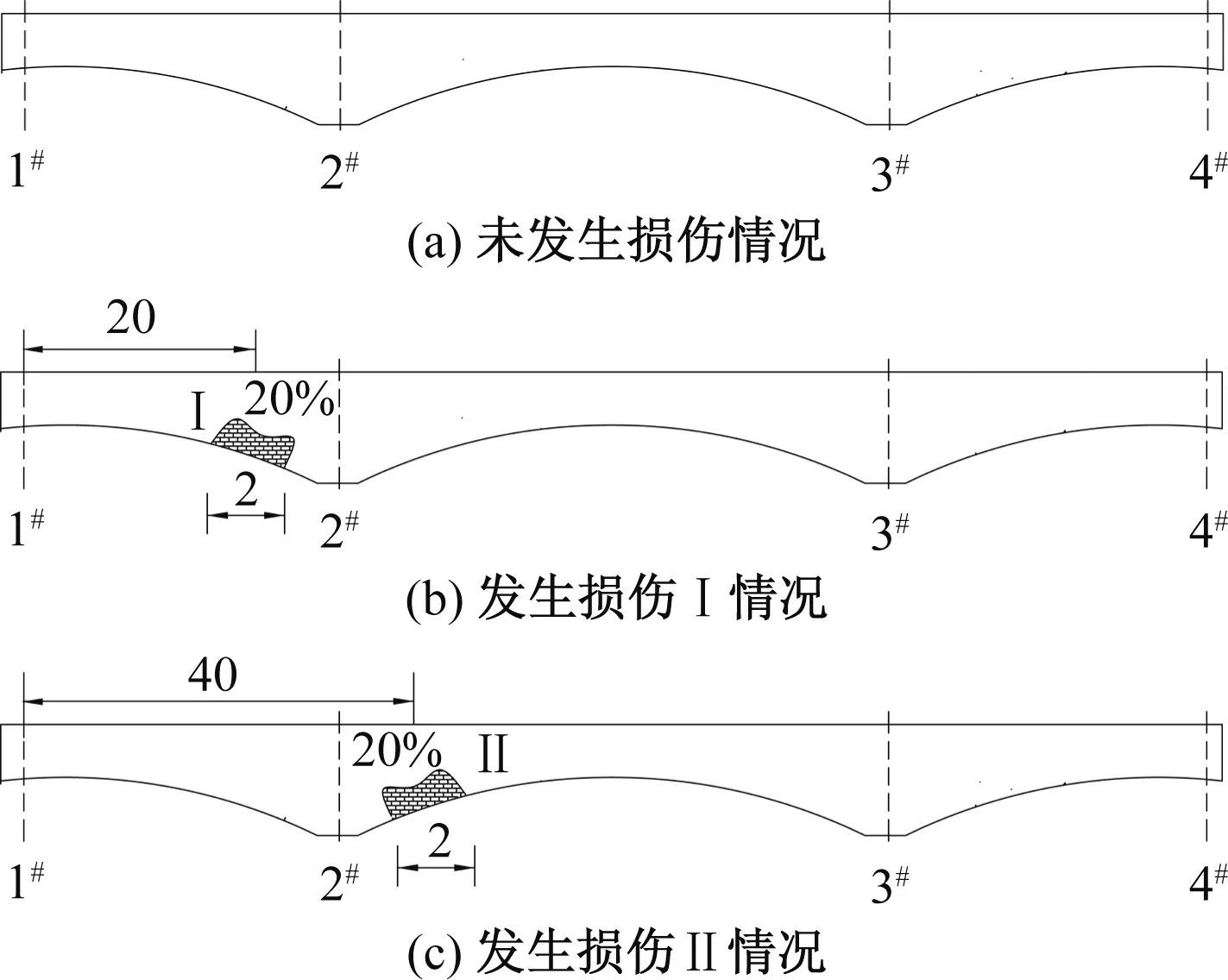
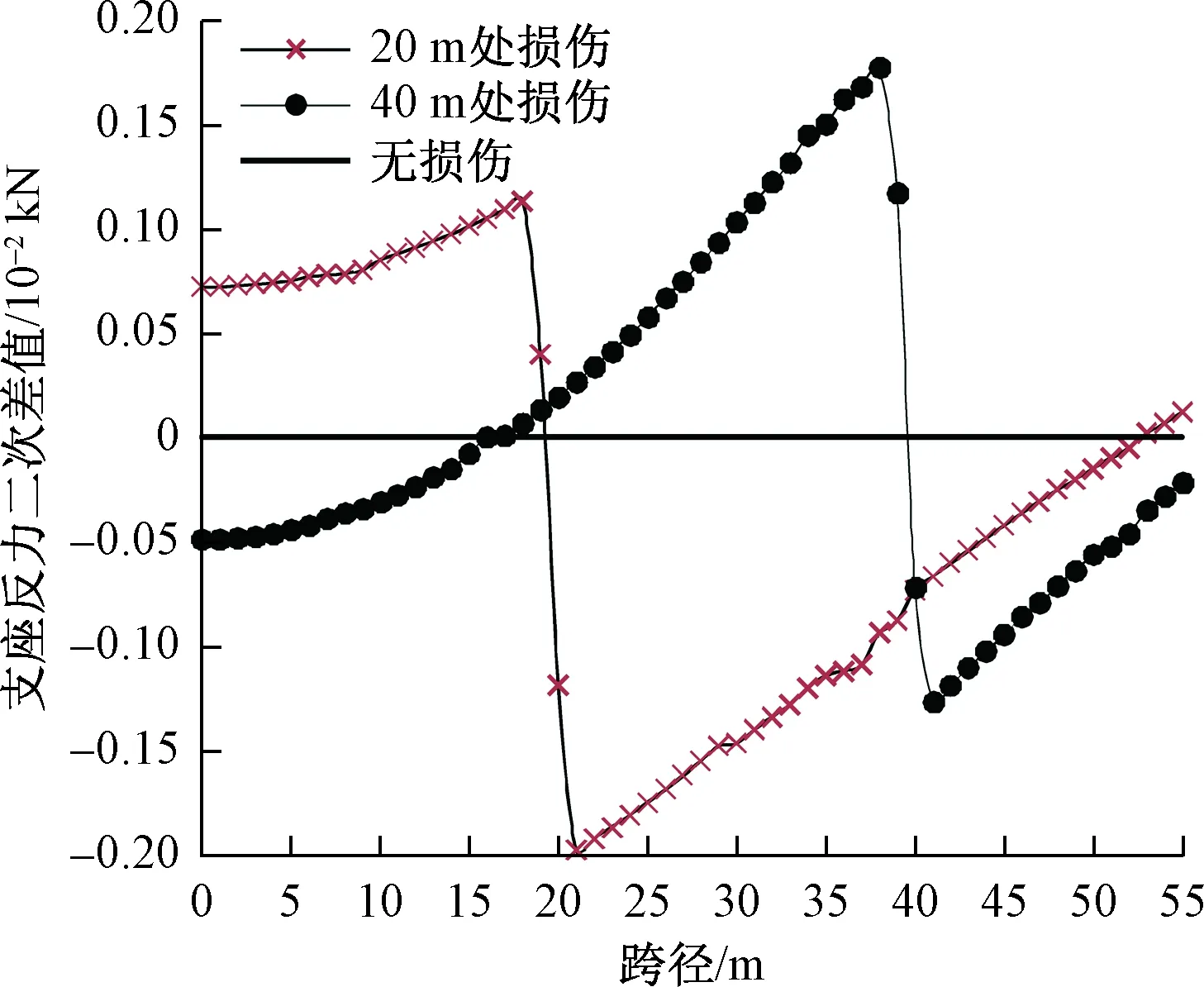
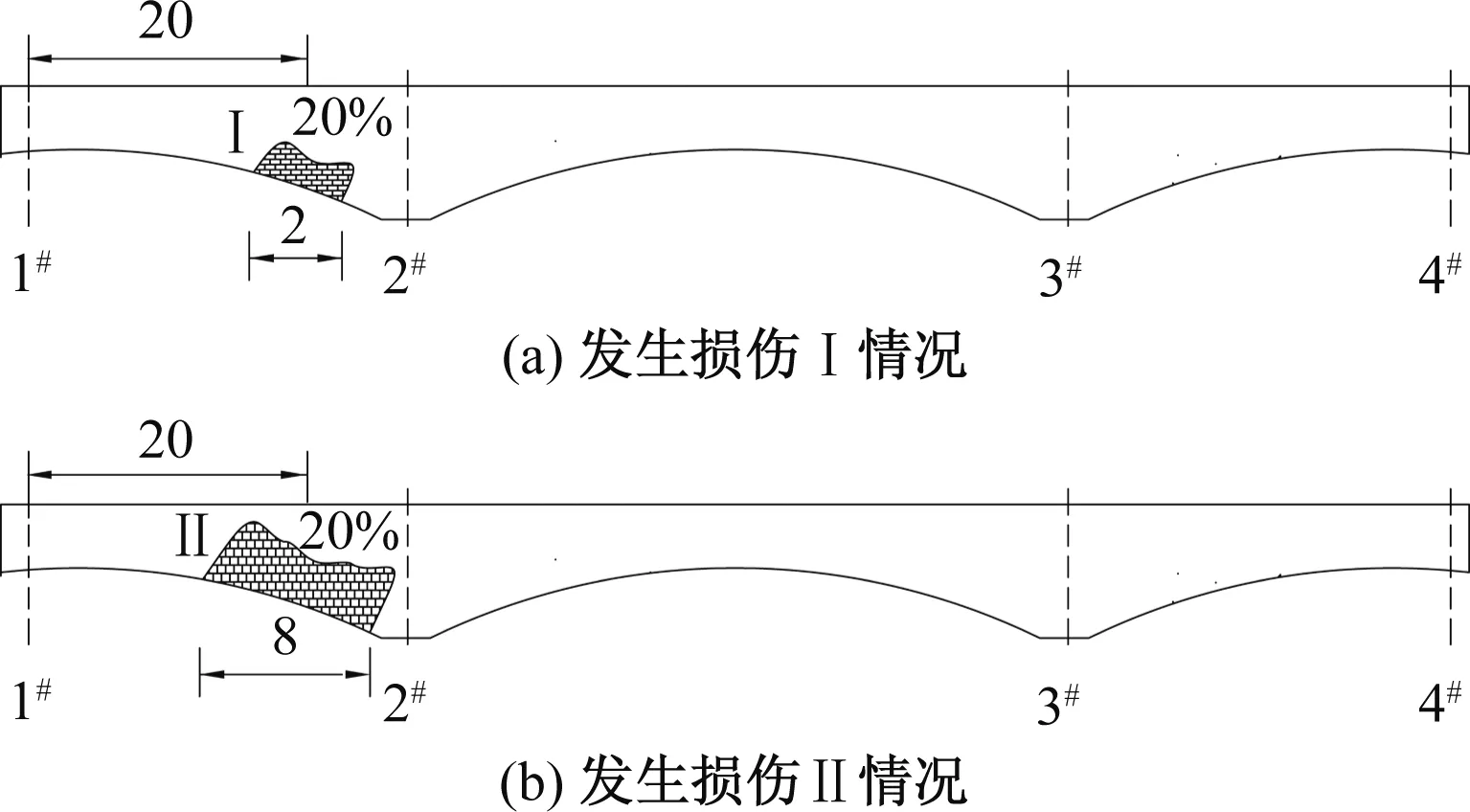
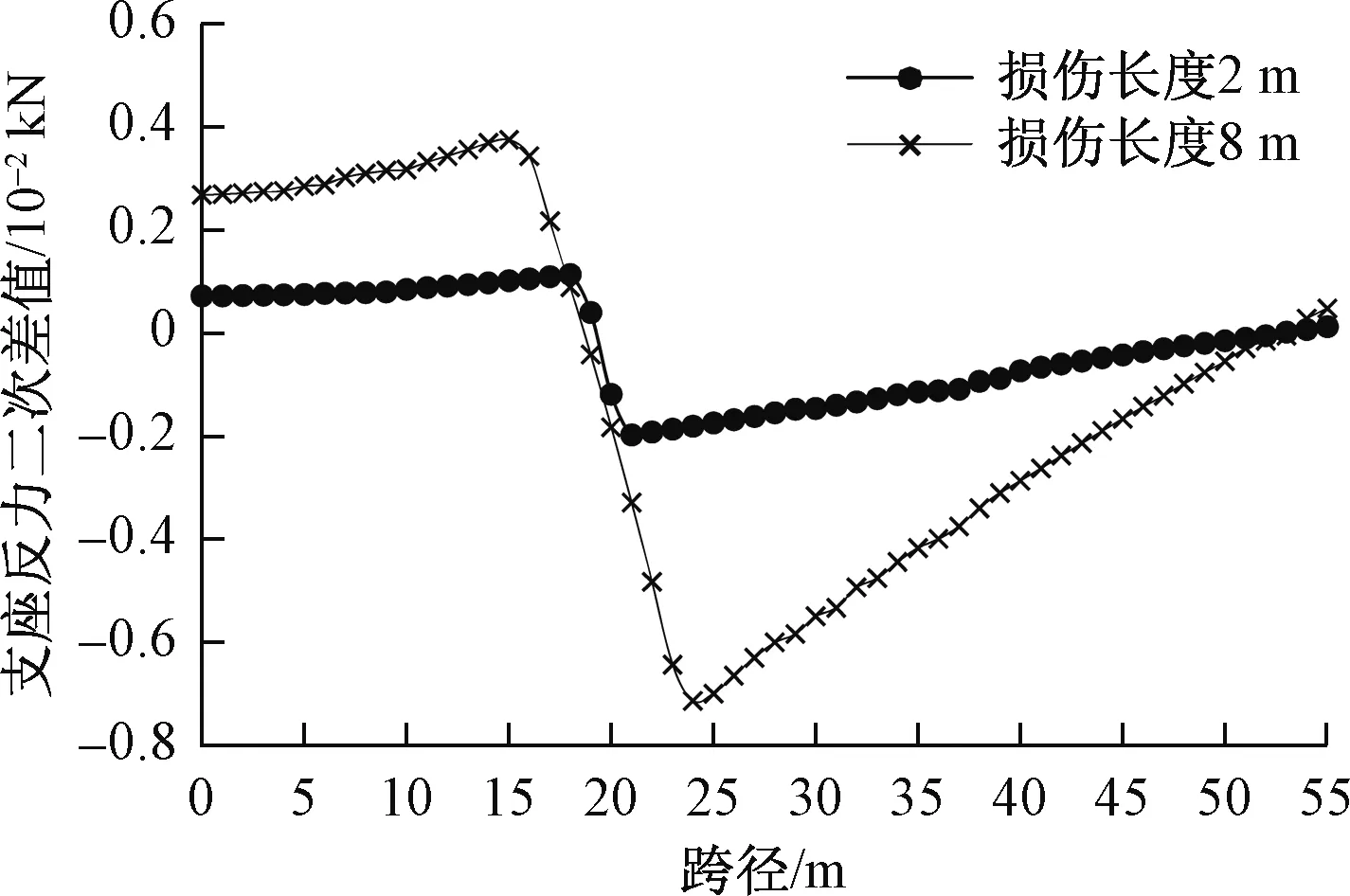
将式(4)、式(5)、式(8)、式(9)代入式(13)、式(14)得到Δ1P(0 (17) (18) 将式(6)~式(9)代入式(15)、式(16)得到Δ2P的表达式为 (19) (20) 式中:L、L1、L2、L3、L4分别为连续梁总长度、第1、第2、第3跨长度、中支点处等高段长度;EIx为x位置处梁抗弯刚度数值,由式(1)计算;a为荷载P作用位置的坐标值;δ11、δ21分别为桥梁完好时在基本结构2#支座处作用F1=1的力,在2#、3#支座处产生的位移;δ12、δ22分别为桥梁完好时在基本结构3#支座处作用F2=1的力,在2#、3#支座处产生的位移;Δ1P、Δ2P分别为无损伤时荷载F作用在基本结构a时,在2#、3#支座处产生的位移。 (1)正向加载时2#支座反力方程 根据图1所示正向(A-O)加载流程,当荷载P作用到A-O段内的任意位置a时,由式(2)得荷载在对称轴O-O′左侧移动时2#支座反力方程为 (21) 式中:R2为正向(A-O)加载过程中2#支座反力。 (2)反向加载时3#支座反力方程 进行反向(A′-O)加载时,当荷载P作用到(A′-O)段内的任意位置a′时,由式(3)得荷载在对称轴O-O′右侧时3#支座反力方程为 (22) (3)中支座反力一次差值方程 将式(21)与式(22)相减,得到两中支座反力一次差值方程为 R2-R3= (23) 为简化公式令 Δ1=δ11·δ22-δ12·δ21 (24) 根据式(24)可将式(23)整理成为 (25) 当图1中的连续梁无损伤时,连续梁结构在尺寸上完全对称于O-O′轴,同时a′又为a关于O-O′轴的对称位置。因此当荷载P作用到O-O′左侧a处时在2#支座所产生的R2值,与当荷载F作用到O-O′右侧a′处时在3#支座所产生的R3值大小是相等的,此时公式(23)可写成为 R2-R3=0 (26) 经整理,得出式(23)中的各系数为 (27) (28) (29) (30) 对两中支座反力进行二次错位差值,过程如下: (1)由图1知,a′与a、a′-m与a+m、对称于轴O-O′; (2)分别将a+m、a代入式(25)后作差,即可得到两中支座反力的二次错位差值方程为 (31) 在图1中,当三跨变高度连续梁完好时,当荷载P分别作用在对称轴两侧对称处时,2#、3#支座反力相等,二者的反力二次差值曲线恒为水平线。 将a+m、a分别代入式(27)中相减得各系数为 (32) 同理,其他系数为 (33) (34) (35) 为区别桥梁损伤前后的各系数的不同,对损伤后基本参数进行修正。 (36) (37) (38) 式中:w1为先后在无损伤、损伤后的基本结构的2#支座处作用F1=1的力,在2#支座处产生的位移差;δ′11、δ′21分别为桥梁损伤后,在基本结构的2#支座处作用F1=1的力,在2#、3#支座处产生的位移;δ′12、δ′22分别为桥梁损伤后,在基本结构的3#支座处作用F2=1的力,在2#、3#支座处产生的位移;ξi、xi、ci为连续梁第i处损伤区域的抗弯刚度损失率、中心坐标位置、半宽度;w2、w3分别为先后在无损伤、损伤后的基本结构的3#支座处作用F2=1的力,在2#、3#支座处产生的位移差。 Δ′1=δ′11·δ′22-δ′12·δ′21=(δ11-w1)·(δ22-w3)- (δ12-w2)2=(δ11·δ22-δ12·δ21)-(δ11·w3+ (39) 为简化计算,设 则公式(39)简化为 Δ′1=Δ1-w4 (40) 3.2.1 荷载P在损伤区左侧时 (1)损伤后中支座反力一次差值方程(左侧) 如图2所示,当荷载P在损伤区左侧时,可建立该区的两中支点反力一次差值方程为 δ′22·Δx1+δ′12·Δx3-δ′11·Δx4)/(Δ1-w4) (41) 图2 荷载P作用在损伤区左侧 根据损伤区位置(xi-ci,xi+ci),可分别求出式(41)中的各系数表达式为 (42) (43) (44) (45) (2)损伤后中支座反力二次差值方程(左侧) 当荷载P移动至损伤区左侧时,分别将a+m、a代入式(41)作差,得到该区的两中支座反力二次错位差值方程为 (Δ1-w4) (46) 其中将a+m、a分别代入式(42)、式(43)中得 (47) (48) 将a′-m=L-(a+m)、a′=L-a分别代入式(44)、式(45)中得 (49) (50) 3.2.2 荷载P移动至损伤区右侧时 (1)损伤后中支座反力一次差值方程(右侧) 由图2可知,当荷载P移动至损伤区右侧时,可建立右侧区的两中支座反力一次差值方程为 δ′12·Δx3-δ′11·Δx4)/(Δ1-w4) (51) 根据损伤区位置(xi-ci,xi+ci),可分别求出式(51)中的各系数表达式为 (52) (53) 式中:Δx5、Δx6为分别为荷载P先后作用在无损伤和损伤后的基本结构a处,在2#、3#支座处产生的位移差。 (2)损伤后中支座反力二次差值方程(右侧) 当荷载P移动至损伤区右侧时,分别将a+m、a代入式(51)作差,得到该区域的两中支座反力二次错位差值方程为 (Δ1-w4) (54) 其中将a+m、a代入式(52)、式(53)中相减得 (55) (56) 3.2.3 当移动荷载P作用在损伤区域时 (1)损伤后中支座反力一次差值(损伤区) 在图2中,当荷载P移动至损伤区时,可建立损伤区的两中支点反力一次差值方程为 δ′11·Δx4]/(Δ1-w4) (57) 根据损伤区位置(xi-ci,xi+ci)可分别求出以上表达式中的各系数表达式为 (58) (59) 式中:Δx7、Δx8为先后在无损伤、损伤后的基本结构a处作用荷载P,在2#支座处产生的位移差;Δx9、Δx10为先后在无损伤、损伤后的基本结构a处作用荷载P,在3#支座处产生的位移差。 (2)损伤后中支座反力二次差值方程(损伤区) 当荷载P移动至损伤区域内时,分别将a+m、a代入式(57)并作差,即可得到损伤区域上的两中支座反力二次错位差值方程为 (60) 其中,将a+m、a分别代入式(58)中相减得 (61) (62) 将a+m、a分别代入式(59)中相减得 (63) (64) 整理式(46)、式(54)、式(60)发现,荷载移动到损伤区、损伤区左、右两侧的中支座反力二次差值方程的表达式中,不相同部分为 (65) (66) (67) 相同部分为 (68) 通过观察以上各式发现,所有表达式中有x、a、P、L、L1、L2、L3、ci、ξi、EIx、xi等参量组成。假定以上参数中,除移动荷载P的作用处a为未知变量,其他参数均为已知量,则结论为: (1)式(65)~式(67)是关于移动变量a的三个不相同的连续多项式,恒不相等。因此,当桥梁出现损伤后,在损伤区、损伤左右两侧这三个区的交界处,中支座反力二次差值方程式一定是不连续,曲线存在突变情况。故当荷载P由损伤区左侧进入损伤区或由损伤区进入损伤区右侧时,必然在两交界处会产生两个突变点。 (2)在桥梁损伤后,利用中支座反力二次差值方程求解得到的两个突变点的位置、数量、水平距离等信息,能够判断出桥梁的损伤位置、损伤数量、损伤范围等信息。 图1为三跨预应力钢筋混凝土连续梁,计算跨径分别为30、50、30 m,中支点等高度区长度为2 m,混凝土C50,预应力筋为12φs15.2,梁高和底板厚呈抛物线变化。截面尺寸见图3。 图3 连续梁跨中和支点截面尺寸(单位:cm) 先对图1中的无损伤变高度连续梁的抗弯刚度进行计算,结果见图4。利用文中方法计算得到的三跨变高度连续梁抗弯刚度曲线与MIDAS计算曲线一致。都表现为越靠近两中支点处的抗弯刚度值越大,在两中支点处达到最大值,而跨中位置的抗弯刚度值最小,计算结果符合实际,表明刚度模型可以用来研究变高度连续梁问题。 图4 三跨变高度连续箱梁抗弯刚度结果 4.3.1 损伤位置 梁未发生损伤、在20 m与40 m处出现2 m长的损伤带(损伤率均为20%)情况见图5。 图5 损伤位置不同时的计算方案(单位:m) 利用文中方法计算出来的不同损伤位置时中支座反力二次差值曲线,见图6。由图6可知,当桥梁完好时,中支座二次差值恒为零,其曲线为一条水平线。同时发现,其他两条曲线分别在19~21、39~41 m范围内出现突变,突变长度为2 m,曲线突变的位置、突变长度与图5中梁的损伤情况吻合。表明利用文中方法可准确识别出三跨变高度连续梁桥发生损伤的位置。 图6 不同损伤位置时中支座反力二次差值曲线图 4.3.2 损伤程度 如图7所示为连续梁在20 m位置处出现了2 m长的损伤带(损伤率分别取20%、30%)。 图7 损伤程度不同时的计算方案(单位:m) 不同损伤程度时中支座反力二次差值曲线,见图8。由图8可知,两条曲线均在19~21 m范围内发生突变,突变长2 m,突变情况与图7中的损伤情况吻合。并且30%损伤率的曲线斜率要比20%损伤率的曲线斜率突变幅值大。 图8 不同损伤程度时中支座反力二次差值曲线图 4.3.3 损伤区域长度 连续梁在20 m处分别出现为2、8 m长损伤带,见图9。 图9 损伤范围不同时的计算方案(单位:m) 不同损伤长度时中支座反力二次差值曲线,见图10。由图10可知,两曲线分别在19~21 m、16~24 m范围处出现了突变,突变区段长分别为2 m和8 m。与图9所示桥梁的损伤位置、损伤长度吻合。对比发现当桥梁的损伤范围越大,中支座反力二次差值曲线的突变区段越长。并且曲线突变区段长度就是桥梁的损伤长度。 图10 不同损伤长度时中支座反力二次差值曲线图 4.3.4 损伤数量 如图11(a)所示,在10、35、50 m处同时出现长度为2 m的三处损伤带;如图11(b)所示,在60、75、100 m处同时出现长度为2 m的三处损伤带。 图11 多处损伤时的计算方案(单位:m) 中跨跨中截面左侧多处损伤时支座反力二次差值曲线图,见图12(a)。由图12(a)可知,曲线发生了三处突变,其突变出现在9~11、34~36、49~51 m范围,突变长度为2 m。并且当损伤出现在中跨跨中截面的左侧时,曲线的突变斜率均为负。 图12 左侧和右侧多处损伤时支座反力二次差值曲线图 中跨跨中截面右侧多处损伤时支座反力二次差值曲线图,见图12(b)。由图12(b)可知,曲线也发生了三处突变,其突变出现在59~61、74~76、99~101 m范围,突变长度为2 m。并且当损伤出现在中跨跨中截面的右侧时,曲线的突变斜率均为正。 可见图12中的曲线突变位置与突变数量规律与图11中的连续梁发生的多处损伤位置、损伤长度等情况相符。表明支座反力二次差值曲线的突变数量就是连续梁的实际损伤数量,同时根据突变曲线的斜率正、负值,可进一步判断出损伤区域位于在中跨跨中截面的左侧或右侧。在实际的检测过程中,可利用这些规律来识别出损伤数量。 (1)变高度连续梁的刚度沿梁长方向是变化的,文中建立的整体化刚度模型能实现变高度连续梁刚度不连续变化情况。 (2)当三跨变高度连续梁完好时,中支座反力二次差值曲线无突变;当发生损伤时,中支座反力二次差值曲线出现突变,其突变的位置、范围、数量分别对应桥梁损伤的位置、长度、数量。 (3)在桥梁检测过程中,基于文中的方法分析中支座反力二次差值曲线的变化情况,就能识别出桥梁损伤的具体位置、范围、数量等桥梁损伤识别的关键信息。 (4)另外,目前关于测取桥梁支座反力大多都是通过千斤顶来测量,测量方法较单一,下一步工作将需要开发一种高效的支座反力测量系统,进而配合文中的理论研究成果来进行实际的桥梁损伤识别。2.3 无损伤时中支座反力一次差值方程
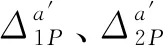


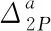

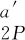
2.4 无损伤时中支座反力二次差值方程


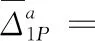
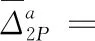


3 损伤后中支座反力二次差值方程
3.1 损伤后基本参数修正
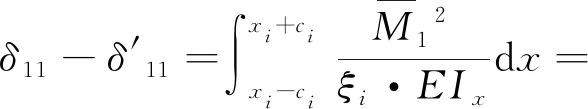
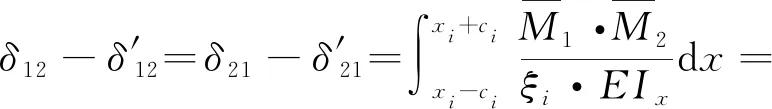
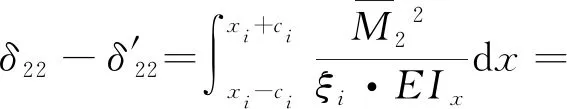

3.2 损伤后中支座反力二次差值方程





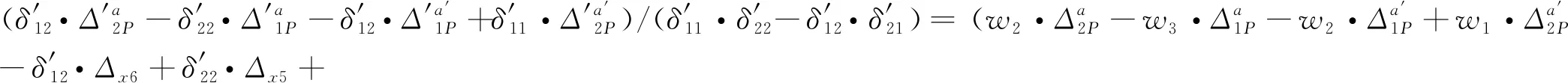


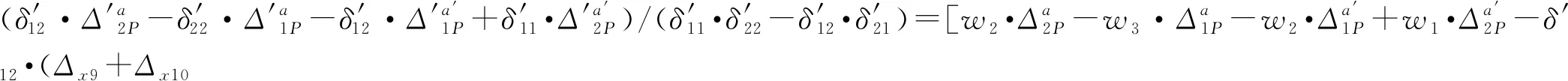
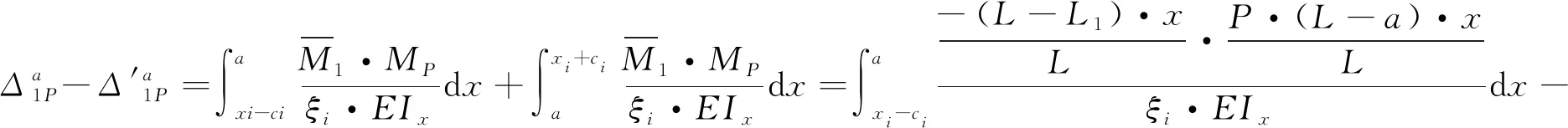



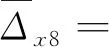


3.3 损伤识别分析
4 结果分析
4.1 算例
4.2 变高度连续梁抗弯刚度计算结果

4.3 损伤识别计算规律分析




5 结论
