基于最小二乘法曲线拟合的轨距参数测量方法

史红梅,许 明,余祖俊

(1.北京交通大学 机械与电子控制工程学院,北京 100044；2.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)

铁路行业近年来在高速和重载两方面得到了快速发展,行车密度大大增加,也对铁路基础设施的状态提出了新的要求,及时检测铁路基础设施状态成为保障铁路交通顺利运行的重要基础。轨距对评价线路质量、指导轨道养护维修作业和保证行车安全非常重要,是轨道检测最基础的一项指标,快速及时地掌握轨距参数具有重要的意义。

根据中国铁路总公司2014年颁布的《铁路技术管理规程》[1],轨距是钢轨头部踏面下16 mm范围内两股钢轨工作边之间的最小距离。直线轨距标准为1 435 mm[1]。传统的轨距测量方法主要采用人工机械测量,实际使用中效率低,而且耗费大量的人力物力；或者采用光电传感器及伺服进行现场测量,它的主要缺点为现场机械振动容易造成伺服机构的磨损破坏[2]。随着非接触式测量技术的发展,基于机器视觉技术的轨距检测方法已经得到越来越广泛的应用[3-5]。测量钢轨轨距参数的研究重点是在获取钢轨轮廓信息后,运用合适的算法实现轨距点的快速精确定位以准确计算轨距值[6]。

本文设计了一套安装在手推式轨道检测小车上的轨距参数测量系统,利用左右钢轨两侧共四台二维激光三角传感器采集钢轨断面轮廓,通过对采集轮廓进行旋转平移并利用改进的ICP算法标定,得到轨道基准坐标系下的钢轨轮廓。利用最小二乘法拟合轨顶部分轮廓曲线,在连续的轮廓曲线上提取轨面下方16 mm处的轨距特征点,从而实现轨距点的定位,计算轨距,实现了轨距的高精度非接触式测量,误差在±1 mm范围内。

1 轨距测量系统的方案

轨距测量系统方案系统框图见图1。本文设计的轨距测量系统采用基于激光三角测量原理[7]的二维激光三角传感器ZLDS200作为测量部件,在水平方向和垂直方向的测量范围分别为170、350 mm,最大测量频率3 000 r/s,在手推车速度1 m/s的情况下,最小采样间隔0.3 mm。系统包括四个二维激光传感器,每两台一组,分别测量左轨和右轨的断面,四个传感器通过以太网接口与笔记本电脑相连。笔记本电脑实现数据采集、标定还原、曲线拟合和轨距计算。为保证四个二维激光传感器采集的是同一个断面,使传感器在外触发方式下工作,将一定频率的脉冲信号接入传感器的同步端子,在脉冲信号上升沿时刻同步测量输出结果数据。为了获取轨距测量位置信息,安装编码器记录小车行走位移,作为钢轨断面的位置标签。

图1 系统原理框图

为了精确测量轨距,需要将四个传感器安装在同一竖直面来保证激光传感器扫描的是同一平面,同时要注意传感器与钢轨的角度,使钢轨断面在激光传感器的量程范围内,能够扫描出完整的钢轨轨头断面。传感器安装位置示意见图2。

图2 传感器安装位置示意

本文设计的轨距测量系统安装在一辆手推式钢轨全断面检测车上,传感器实际安装效果见图3,两个激光二维扫描传感器可以采集轨顶踏面的全部轮廓,同时也能采集轨顶踏面下方16 mm处的轮廓,两个传感器的激光带位于同一平面,既保证了采集到的轮廓属于同一钢轨断面,也避免了传感器之间的相互干扰。

图3 传感器实际安装效果

2 基于改进ICP算法的传感器标定

2.1 传感器标定的原理

二维激光传感器输出的测量点坐标是基于传感器坐标系的,将其转换到轨道基准坐标系下才能用于轨距计算。传感器坐标系与轨道基准坐标系的相对位置见图4。

图4 传感器坐标系与轨道基准坐标系的相对位置

本文定义轨道基准坐标系以左轨轨底中心为原点,垂直轨道方向为X轴,竖直方向为Y轴,沿轨道方向为Z轴,而传感器坐标系则是以传感器水平方向为U轴,传感器垂直方向为V轴,垂直激光平面方向为W轴,将传感器坐标系下坐标(U,V,W)转换到轨道基准坐标系下坐标(X,Y,Z)的过程称为传感器的标定[8-14]。

激光三角传感器的标定是将测量点的坐标从传感器坐标系转换到轨道基准坐标系的过程,通过旋转和平移使实现两个坐标系的转换。传感器坐标系相对于轨道基准坐标系的旋转角度分别为α、β、θ,两个坐标系原点的在三维坐标下的距离分别为Δx、Δy、Δz,两个坐标系变换公式为

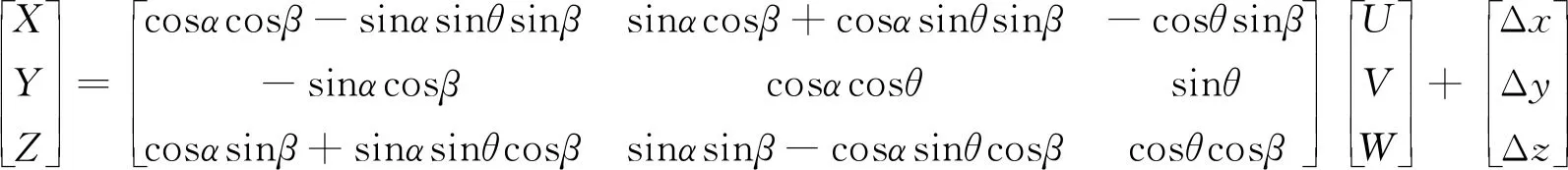
( 1 )

定义旋转矩阵

( 2 )

平移矩阵

( 3 )

2.2 传感器的标定过程

对传感器的标定过程,实质上就是求取目标点集和传感器点集之间的旋转矩阵R和平移矩阵T的过程,也就是点集配准。本文采用迭代最近算法即ICP算法计算R和T。标定过程以传感器在无磨耗的标准60钢轨上采集的轮廓数据作为传感器点集,以标准60钢轨的截面轮廓点数据作为目标点集。

ICP算法是点集精确匹配中一种重要的算法。ICP算法通过迭代计算使对应点对距离均方误差最小。ICP算法复杂度较高,运行时间长,为了提高运算效率,本文对算法进行了改进。本文使用的是二维激光三角传感器,W轴无输出,因此规定某一断面在传感器坐标系下W轴坐标与轨道基准坐标系下Z轴坐标相同,标定被改进为将传感器坐标系下坐标(U,V,Z)转换到轨道基准坐标系下坐标(X,Y,Z)的过程,所以公式(1)变换为

( 4 )

三维点集匹配需要计算传感器坐标系三个坐标轴的偏转角α、β、θ和偏移量Δx、Δy、Δz共六个参数,而二维点集匹配只需要计算传感器坐标系在XY平面内的偏转角α和偏移量Δx、Δy三个参数,运算时间大大减少。进一步改进,在标定过程中不加入Z轴坐标,上述公式变为

( 5 )

通过这种方法,将三维点集匹配转换成了二维点集配准,减少了运算量,提高了运算效率。

ICP算法迭代停止的标志是两组点集距离小于给定的阈值或超过最大迭代次数,迭代次数越多,算法运行时间越长。当ICP算法因迭代次数达到最大值而停止迭代时,如两组点集距离仍然过大,则不能满足匹配精度。针对这个问题,本系统首先对传感器点集粗配准,根据传感器设计安装位置,先对传感器点集进行一次旋转平移,使其与轨道基准坐标系下的钢轨轮廓具有较大的相似性。

设初始旋转矩阵为R0,初始平移矩阵为T0,传感器采集的钢轨轮廓点集N(i)的坐标为(U(i),V(i)|i=1,2,3,…,n),粗配准后点集N(i)变换为点N′(i),坐标为(U′(i),V′(i) |i=1,2,3,…,n),变换公式为

( 6 )

变换后得到的点集N′与匹配目标点集M已经具有很高的相似性,匹配得出的旋转矩阵R和平移矩阵T的准确度将提高。在得到经过粗配准的钢轨轮廓点集之后,运行ICP算法,计算两个匹配点集之间的旋转矩阵R和平移矩阵T。

经过粗配准和ICP算法匹配后,传感器采集的轮廓点坐标已经从传感器坐标系转换到轨道基准坐标系下,可以用于轨距点的定位计算。由传感器采集的原始数据点(U,V)到轨道基准坐标系下的轮廓点(X,Y),其变换过程为

( 7 )

所以,标定矩阵最终为

TR=RR0

( 8 )

TT=RT0+T

( 9 )

左侧钢轨两台传感器采集到的原始轮廓图像见图5(a),经过标定的轮廓曲线见图5(b)。

图5 标定前后钢轨轮廓图像

3 轨距点的定位

为了计算轨距参数,首先要确定位于钢轨轮廓图像上的轨距特征点。由于采集数据是钢轨轮廓上的离散点,很可能不包含轨距点,造成轨距点定位不准,本文提出了一种利用曲线拟合的方法定位轨距点。

3.1 定位轨距点的算法流程

轨距点的定位算法流程见图6,根据轨距定义,轨距点位于钢轨顶面下16 mm处内侧,要计算轨距,首先需要确定钢轨轮廓顶面下方16 mm处的位置。做轨顶曲线的水平切线,在向下平移16 mm得到特征直线,特征直线与钢轨内侧轮廓的交点即钢轨轮廓点。

图6 轨距算法流程图

本文采用曲线拟合的方法消除基于离散轮廓点定位轨距点引起的误差,其优点在于将离散的轮廓点集拟合为连续的轮廓曲线后,消除了传感器分辨率对测量结果的限定。下面详细介绍轨距点定位的算法流程。

3.2 曲线平滑

受传感器测量误差和噪声的影响,传感器采集到的钢轨轮廓存在不平滑现象。为了更好的进行钢轨轮廓曲线拟合,要对采集数据进行曲线平滑。本文采用了一种自适应平滑滤波方法[15],根据信号的连续度变化进行卷积迭代对钢轨轮廓进行平滑处理。具体方法如下:

传感器采集到钢轨轮廓数据通过标定矩阵旋转平移得到基于轨道基准坐标系下的数据,设P为轮廓线上所有坐标点p(i)的集合为

P={p(i)=(x(i),y(i))|i=0,1,…,n-1}

式中:n为坐标点的个数。

设S(x)为未经平滑的一维离散信号,经(t+1)次迭代平滑后的信号可表示为

(10)

其中

(11)

式中:k(t)(x+i)≥0(-N≤i≤N)为卷积的权值；N为选取邻近点的个数。对于自适应平滑,N=1,k(t)(x)随着信号在x处的不连续度的增大而减小。此外选取

(12)

式中:S′(t)(x)为信号S(t)(x)的导数,其离散形式可表示为

(13)

使用该算法实现平滑的效果主要由σ和t两个参数决定,σ表示了平滑程度的大小,而t代表迭代次数,通过一系列实验推算,最终本文选取σ=0.2,t=5,能够较好的实现钢轨轮廓平滑,消除噪声。图7(a)和图7(b)分别是曲线平滑前后的采集轮廓与标准轮廓图形,可以发现轮廓噪声明显减小。

图7 曲线平滑前后的采集轮廓与标准轮廓

3.3 轨顶轮廓曲线的拟合

平滑后得到的钢轨轮廓为一系列离散点,采用最小二乘法拟合钢轨轮廓曲线。钢轨轮廓是由一系列圆弧拼接组成,不可能用一个曲线方程描述整个轨头部分。拟合轮廓曲线的目的是获取钢轨顶面切线,只研究轨顶半径为300 mm部分圆弧拟合即可,本文提出了基于最小二乘法的圆弧拟合方法。

轨顶部分的轮廓点是轮廓线上所有点中最高的N个点的合集,设Q为轮廓线上位于轨顶部分的坐标点q(i)的合集为

Q={q(i)=(x(i),y(i))|i=0,1,…,N-1}

根据经验,这里N取50。

设轨顶圆弧曲线是圆心为(A,B),半径为R的圆的一段圆弧,根据一系列离散点q(i),利用最小二乘法拟合圆的方程。

圆的方程为

R2=(x-A)2+(y-B)2

(14)

即

x2+y2+ax+by+c=0

(15)

式中:a=-2A,b=-2B,c=A2+B2-R2。

轮廓点q(i)到圆心的距离d(i)为

d2(i)=[x(i)-A]2+[y(i)-B]2

(16)

轮廓点q(i)到圆心的距离的平方与半径平方的差为

δ(i)=d2(i)-R2=[x(i)-A]2+[y(i)-B]2-R2=x2(i)+y2(i)+ax(i)+by(i)+c

(17)

令Q(a,b,c)为δ(i)的平方和，即

Q(a,b,c)=∑δ2(i)=∑[x2(i)+y2(i)+ax(i)+

by(i)+c]2

(18)

因为Q(a,b,c)的值不能为负,因此必然存在一组参数(a,b,c)使Q(a,b,c)取最小值。

Q(a,b,c)对a,b,c求偏导,令偏导等于0,得到极值点,比较所有极值点的函数值即可得到最小值。

(19)

(20)

(21)

解这个方程组,可得

(22)

(23)

(24)

其中

f(x,y)=N∑x2(i)-∑x(i)∑x(i)

(25)

g(x,y)=N∑x(i)y(i)-∑x(i)∑y(i)

(26)

h(x,y)=N∑x2(i)-N∑x(i)y2(i)-∑[x2(i)+y2(i)]∑x(i)

(27)

k(x,y)=N∑y2(i)-∑y(i)∑y(i)

(28)

l(x,y)=N∑x2(i)y(i)+N∑y2(i)-∑[x2(i)+y2(i)]∑y(i)

(29)

轨顶部分曲线为圆上的一段圆弧,轨顶部分曲线S的定义域为{min[x(i)],max[x(i)]},曲线S的表达式为

x2+y2+ax+by+c=0

min[x(i)]

(30)

3.4 轨距点的定位

轨距点定位过程示意见图8。在得到轨顶轮廓曲线S后,可以做出轨顶的水平切线L0,向下平移16 mm得到直线L1,直线L1与钢轨内侧轮廓的交点即钢轨轮廓点。由于钢轨轮廓P为一系列离散的点的合集,因此可能不存在与直线L1的交点,因此同样需要利用最小二乘法拟合出钢轨内侧与直线L1相交的轮廓曲线。取钢轨内侧与直线L1距离最小的10个点,同样采用最小二乘法拟合轮廓曲线,根据60型钢轨截面可知,轨距点位于一段坡度为1∶20的直线上,据此拟合得到一条直线L2,将拟合得到的直线L2和直线L1求交点g,即可得到轨距特征点的坐标。利用同样的方法求另一条钢轨轨距特征点的坐标,在钢轨基准坐标系下求两个轨距特征点的距离,即可计算得到轨距。

图8 轨距点定位过程示意

4 试验与误差分析

4.1 试验验证

为了验证轨距测量系统精度和误差,本系统分别在实验室环境下和环形铁道试验场进行了试验验证,环形铁道试验场试验现场图，见图9。

图9 环铁试验现场

将测量结果与测量精度为±0.2 mm的0级轨距尺的测量结果进行比较。试验分为两部分:第一部分,在实验室环境下可变间距的钢轨试验台上从1 430 mm至1 439 mm范围内,每隔1 mm测量一次轨距值,见表1。

表1 不同轨距值下系统测量值 mm

第二部分,在环形铁道试验场进行现场试验,选取钢轨上多个位置,采用本文提出的测量方法和轨距尺多次测量该位置的轨距值,得到的部分数据见表2。

通过对结果进行对比并经过多次重复性试验,本文提出的算法可以有效测量出钢轨的轨距参数,检测精度达到±1 mm。

表2 轨距试验测量结果 mm

4.2 误差分析

对试验结果进行误差分析,总结得出轨距测量系统的误差主要来源于两个方面:传感器测量误差以及手推式轨检车机械结构造成的误差。

激光传感器采用的激光三角法测距,除了本身光学部件造成的误差以外,还受到测量环境、被测物体表面特性、发射光强及光束直径大小等因素干扰[16]。本文所使用的二维激光三角传感器在水平方向的最大测量误差为0.340 mm,在垂直方向的最大测量误差为0.525 mm。

为了使小车在钢轨上顺利通行,手推式轨检车的行走轮侧边与钢轨内侧存在一定的间隙,由于间隙的存在,手推式轨检车在钢轨上运行并非贴紧一侧钢轨前行,传感器坐标系与轨道基准坐标系的相对位置不固定,传感器的采集位置与标定时的位置存在误差,引入标定矩阵后,还原得到的断面与真实断面存在微小的差别,计算得到的轨距出现误差。

钢轨工作边在长期工作后会出现磨耗现象,廓形发生改变,与标准的钢轨轮廓有差异。由于磨耗造成的钢轨轮廓形状情况复杂,本文提出的轨距点定位方法不能针对其中一些情况准确定位出轨距点,造成了误差。

5 结论

本文设计的钢轨轨距检测系统采用基于激光三角测量原理的二维激光三角传感器为测量部件,采用非接触式测量方法,采集钢轨轮廓点坐标。利用改进ICP算法将采集的钢轨轮廓与钢轨标准轮廓相匹配,实现系统标定,完成将传感器坐标系到轨道基准坐标系的转换。在轨距特征点定位上,本文提出了一种基于最小二乘法进行轨顶曲线拟合的算法,在连续的轮廓曲线上定位轨距点,相比在离散轮廓点集提高了定位精度。通过现场试验验证,系统可以准确轨距参数,检测精度达到了±1 mm。