基于XGBoost算法的铁路旅客退票率预测研究

王红爱

(中国铁道科学研究院,北京 100081)

退票是铁路客票发售和预订系统(以下简称客票系统)的核心业务之一[1],当旅客行程变更或自然灾害、调整运行图等事件发生时,可通过办理退票手续来取消旅行。目前有4种办理退票的渠道,分别为窗口退票、互联网退票、手机退票、自助设备退票,多渠道办理大大提高了旅客办理退票业务的便捷性。退票后系统会将席位从“已售”状态变更为“未售”状态,初始的一个长途席位可能会被分成多个短途席位,组织该部分席位进行再售,对退票席位充分使用,一直是铁路部门研究的重要课题之一,也是铁路收益管理的重要内容之一。对预售期内的空闲席位,包括通过办理退票、改签、作废票等业务释放的席位,国内外都实施了不同的售票组织策略。国外铁路部门[2-3],如美国,建立了ARROW客票预订系统,通过价格浮动,合理分配运输能力；法国国家铁路公司(SNCF)采用SABRE方案寻求最大化的收益增加方案,使得所有列车的席位分配达到最优；英国大东北铁路公司(GNER)采用IRIS工程方案,通过预测需求及采用折扣票价实现席位的最大化利用。国内铁路部门实施了席位合并、预分、复用、共用、取消限售等不同策略[4-6],并将释放的空闲席位随机转到网上进行公开发售,以避免“随返随放”导致囤票倒票现象。为实现“票尽其用”的目标,铁路部门对空闲席位制定了多方位的售票组织策略,但还没有对未来“可能”的空闲席位进行智能化管理,本文旨在从铁路客票系统的历史客票数据中,通过智能化技术,挖掘有用的信息,提前对因退票而释放的席位情况进行预测,为票额再售提供决策依据,为旅客购票提供更多选择。

文中将退票率作为目标变量,对其进行预测研究,从旅客来说,可以根据预测结果规划购票需求,对退票率高的意向列车进行候补下单,对退票率低的意向列车可以更换其他购票成功率高的列车进行下单；从客票系统来说,可以根据预测结果对候补购票的排队数量进行动态调整,避免票额能力不足而排队过长造成的访问资源浪费,并且可以提升旅客购票体验；从铁路部门来说,可以根据预测结果提前对票额进行动态调整,制定共用、取消限售等策略,满足更多旅客的出行需求；从车站来说,可以根据预测结果实行弹性开窗机制,节约旅客退票排队时间。

目前对客票系统历史数据的研究,主要是基于不同的学习算法进行模型研究,如BP人工神经网络[7]、灰色动态模型[8]、灰色-马尔科夫预测模型[9]、XGBoost(Extreme Gradient Boosting)算法[10]、遗传算法[11]等。XGBoost机器学习算法[12]是近年来新兴的一种高效算法,能够自动利用CPU的多线程进行并行处理,在效率及精度上都比较有优势,故在本文中采用了XGBoost算法进行退票率的分类及预测研究,研究中对客票数据进行了脱敏处理。在进行分类预测前,首先对退票率数据做预处理,根据退票业务特点,分析影响退票率的特征变量,并且为满足分类算法的要求,需要对退票率数据进行离散化处理。

1 退票率数据预处理

1.1 退票率的特征提取

退票率是指退票量占售出量的比例,是对某列车或多列车同一天同一区段同一席别的席位退票情况的统计指标之一,退票率Rijk为

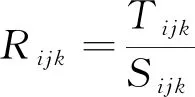
(1)

式中:Tijk为某天第i趟车第j个区段第k个席别的退票量；Sijk为某天第i趟车第j个区段第k个席别的售出量。

退票率的统计要依据客票系统的售票、退票交易数据,交易数据包括乘车日期、车次、发站、到站、车厢、席位号、售出渠道、售出时间等属性。影响退票率的特征变量见表1,包括时间特征、区段特征、席别特征、售出特征,其中,时间特征依据节假日特点划分售出时间属性值；区段特征依据车票发站、到站与始发站、终到站的关系划分属性值；售出特征中“售出渠道”子特征,包括互联网、手机APP、车站窗口、TVM、电话订票几类属性值。文中将售出特征中的各子特征与各主特征一起作为特征变量,退票率作为目标变量进行分类及预测研究,在研究过程中对原始数据依据特征变量进行统计,获得售出量及退票量以进行退票率的计算。

表1 影响退票率的特征变量

1.2 退票率的离散化

为避免样本偏差带来的噪声问题,对目标变量采用无监督离散化。离散化[13-16]即将样本数据划分为多个空间,每个空间由一个离散的值来标识。无监督离散化算法[17]包括等宽离散化方法(Equal Width，EW)、等频率离散化方法(Equal Frequent，EF)、近似等频离散化方法(Approximate Equal Frequency Discretization Method，AEFD)、基于局部密度的离散化算法、基于聚类的离散化算法等。其中,DBSCAN[18](Density-Based Spatial Clustering of Applications with Noise)是基于密度的优秀聚类算法,它把具有足够高密度的区域划分为簇,将簇定义为密度相连的点的最大集合,可以在噪声的空间数据库中发现任意形状的聚类,并且不需要事先知道要形成的簇类数量。根据业务特点,退票率具有密度不均匀的特征,而经典的DBSCAN算法难以适应密度不均匀的数据集。为解决密度不均匀带来的问题,设计了EW-DBSCAN离散化方法,即首先用等宽离散化方法将样本数据进行离散化,然后将离散化结果中高密度区段采用DBSCAN算法进行二次离散化。实现如下:

Step1取一定时间段的退票率数据,分析数据分布特征。

Step2根据数据分布特征,确定等宽离散化的区间个数。

Step3将退票率数据等宽离散化,并分析各区间的数据密度。

Step4将已划分区间中密度较高的区间通过DBSCAN算法进行二次离散化。

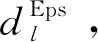
Step6最后将各个局部的聚类结果进行合并。

由于每个局部区域使用的是各自局部的聚类半径值来进行聚类,从而可以有效缓解因使用全局聚类半径值dEps而导致聚类质量恶化的问题。本文取客座率较高的某线列车2017年客票数据,通过Python3.5.1实现该算法,表2为目标离散化结果,取值范围及切分点以百分比为单位。

表2 目标离散化结果

2 退票率分类及预测

2.1 区间退票率的最优值确定

在一些客运业务中,掌握精确值比掌握区间值对旅客、管理部门及客票系统进行决策更有指导性意义,因此为指导退票后的售票策略,本文在每个退票率分类中,计算能满足一定误差范围的最优预测退票率取值,使得该最优预测退票率在误差范围内密度最大。梯度算法具有很强的局部搜索能力,采用梯度算法进行区间退票率最优值计算。取某个离散化区间[Rl,Rl+1],求该区间的最优预测退票率,算法实现如下:

Step1Rl1,Rl2,…,Rln为区间[Rl,Rl+1]上的n个样本数据,给定误差范围[e1,e2]。

Step2根据误差范围,可将样本数据点,分成n个样本区间

{[Rl1-e1,Rl1+e2],[Rl2-e1,Rl2+e2],…,[Rln-e1,Rln+e2]}

Step3统计上述n个样本区间对应的样本数量{Y1,Y2,…,Yn},拟合各区间中位数与样本数量的数据特征曲线

Y=f(X)

式中:X为以各区间的中位数为特征的变量。

Step4给定一个初始点X0,并设定算法终止距离ε以及步长α。

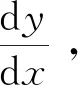
Step6重复计算导数,直至满足算法终止距离ε,计算到的极值即为最优预测退票率。

建立拟合函数,进行梯度算法求最优预测退票率,可以避免直接迭代求最值造成的过拟合问题。

根据实际业务需求,将误差范围设定为[-5%,5%],取客座率较高的某线列车2017年客票数据,拟合误差区间的样本数量。因为业务特点,不会出现整年售出车票大部分被退票的现象,故区间[85,100]数据密度较低,该区间拟合函数特征不太明显,其他区间二次曲线特征明显。样本密度较高的[25%,40%)区间的拟合曲线见图1,最优预测退票率的计算结果见表3。

图1 [25%,40%)区间的拟合曲线图

表3 最优预测退票率的计算结果

2.2 基于XGBoost算法的退票率分类研究

XGBoost是一种可扩展的、分布式的算法库,在GBDT(Gradient Boosting Decision Tree,梯度提升决策树)基础上做了很多优化,如损失函数、正则项、特征选择、并行运算等。XGBoost的集成学习过程为

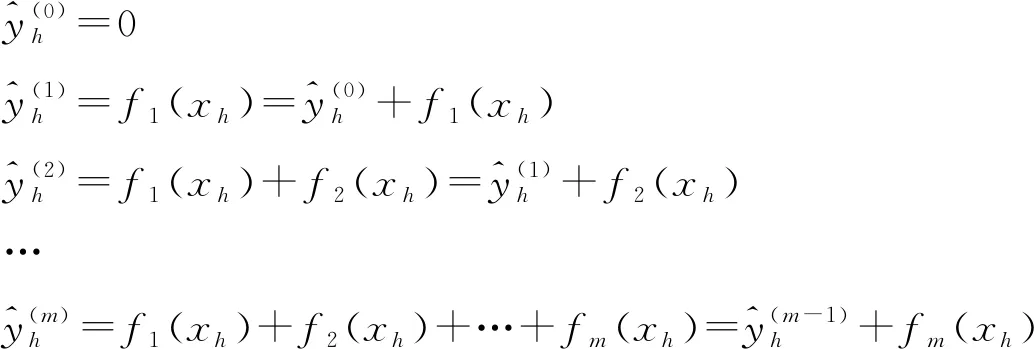
(2)

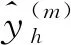
第m次的目标函数为

(3)

基于XGBoost算法的退票率分类实现如下:

Step2初始值设定:设定正则参数p1、p2；设定树的深度；设定树的总量,即要建多少棵树。

Step3计算各样本的Sm函数的一阶导数及二阶导数。

Step4进行建树,核心的裂解过程见图2。

Step5达到树的深度则一棵树建立完成,重复Step3、Step4,直至按照树的总量建立完成,即完成分类。

为了支持自定义损失函数,在XGBoost算法中,需要对损失函数进行二阶泰勒展开

(4)

另外,建树过程中,需要计算增益值,并根据最大增益值来进行分叉处理。增益值Ggain为

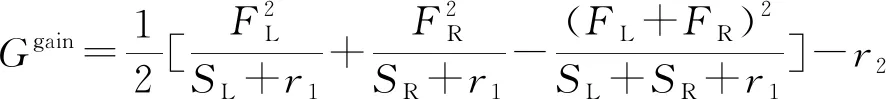
(5)

式中:FL为分裂点的左侧样本一阶导数之和；SL为对应的二阶导数之和；FR为分裂点的右侧样本一阶导数之和；SR为对应的二阶导数之和；r1、r2为常数项,在建树过程中控制了复杂度,取值均为0.1。

图2 XGBoost建树分枝过程

2.2.1 XGBoost算法的参数优化

参数组合对XGBoost算法的分类性能影响较大,一般会运用经验或者穷举法对参数进行调整。因为贝叶斯优化具有迭代次数少,速度快,可以避免非凸函数的局部最优问题等优点,在很多应用[19-20]中调参时选择贝叶斯方法,并取得较好的效果,故选择用贝叶斯方法对XGBoost算法进行参数优化。

贝叶斯调参时需要设定目标函数,本文中,目标函数入参为分类算法XGBoost的所有参数,输出为模型交叉验证5次的AUC均值。依据上文目标离散化中用到的某线列车2017年客票数据,将该数据80%部分进行训练,20%部分进行测试,采用贝叶斯方法对XGBoost算法进行参数最优化,结果见表4,其中迭代8次的参数达到最优。

表4中,参数1=colsample_bytree,表示构造每棵树时的列采样率；参数2=gamma,表示指定节点被分割时,最小损失函数减小的大小；参数3=learning_rate,表示学习率,可以使模型更加健壮；参数4=max_depth,表示树的最大深度,该参数用于控制过拟合；参数5=min_child_weight,表示所有观察值的最小权重和,该参数用于减少过拟合；参数6=n_estimators,表示树的数量,本次调优取值范围[10,100]；参数7=subsample,表示样本的采样率；AUC(Area Under Curve),作为参数最优化的评价标准,取值范围在[0,1]。

2.2.2 退票率预测模型

退票率预测模型见图3。包括模型生成、模型使用、模型评价、模型优化4个阶段。按照模型生成→模型使用→模型评价→模型优化流程进行退票率预测。

模型生成阶段:首先,按照EW-DBSCAN离散化方法对历史退票率进行离散化处理,应用梯度算法对各离散化区间选取最优预测退票率；其次,将历史客票数据按照8∶2的比例,采用基于贝叶斯调参的XGBoost算法进行退票率分类训练和测试。

模型使用阶段:准备待预测数据后,通过生成的模型对此部分数据进行退票率预测。

模型评价阶段:将预测结果与实际退票率进行对比,准度符合要求时,模型无须优化,继续下一次预测。准度不符合要求时,记录预测日志表,当准度不符合要求的累计次数达到阈值时,进行模型优化。

表4 贝叶斯方法对XGBoost算法进行调参

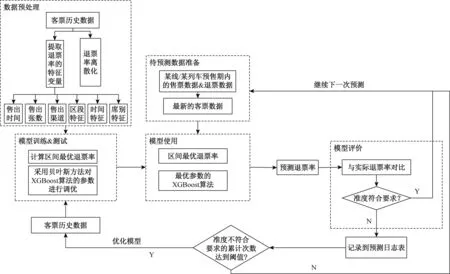
图3 退票率预测模型图

模型优化阶段:以最新客票历史数据为数据源,进行模型训练和测试,重新生成模型,在模型优化阶段,定期依据新数据重新将退票率离散化处理。

3 算法验证

3.1 分类算法有效性验证

分类精度的衡量指标很多,常用的有混淆矩阵、总体分类精度、Kappa系数、ROC曲线等。对于二分类问题,可以使用ROC曲线来评估模型的预测效果；对于多分类问题衡量模型精准度的可以用混淆矩阵、Kappa系数等。混淆矩阵不能直观反映出分类精度的好坏,本文中采用Kappa系数进行算法精度评价,Kappa系数基于实际分类与预测分类的混淆矩阵,表示分类与完全随机的分类产生错误减少的比例,值越大,则代表模型实现的分类准确度越高,在实际应用中,一般取值范围是[0,1]。K为Kappa系数,其计算过程为

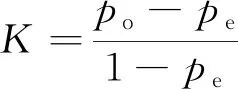
(6)

(7)

3.1.1 基于贝叶斯参数优化的XGBoost算法有效性验证

为了验证基于贝叶斯参数优化的XGBoost算法是否较其他分类算法在铁路退票率分类预测中效果更好,本文同样以客座率较高的某线列车2018年客票数据进行验证,实验环境为Win10,64位操作系统,Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz,内存32 GB,Python3.5.1。表5为基于贝叶斯参数优化的XGBoost算法、基于穷举法的XGBoost算法、GBDT 算法、SVM算法、Adaboost算法、RandomForest算法的Kappa系数验证结果。

表5 不同算法的退票率预测精度对比

由表5可见,相对于其他分类算法, XGBoost算法在预测退票率时有较高的分类精度,基于穷举法的XGBoost算法与基于贝叶斯优化参数的XGBoost算法的预测精度相差不多,但是基于贝叶斯参数优化的XGBoost算法比基于穷举法的XGBoost算法的训练速度快9倍多,因此采用贝叶斯参数优化法进行XGBoost参数调优。XGBoost算法在进行训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,在进行节点的分裂时,对各个特征的增益计算就可以开多线程进行,大大减少了计算量,在生成候选的分割点时体现了高效。

3.1.2 退票率离散化算法有效性验证

为了验证本文中使用的离散化方法在退票率区间分割中更有效,将退票率采用等宽、等频、DBSCAN算法及本文中提出的EW-DBSCAN算法进行对比实验,分类算法均为基于贝叶斯参数优化的XGBoost算法。这几种不同离散化方法后的预测精度对比见表6,其中EW-DBSCAN算法的Kappa指数最高。

表6 不同离散化方法的退票率预测精度对比

3.2 区间最优退票率选取方法有效性验证

为了验证本文中使用的区间最优退票率选取方法的有效性,将各离散化区间分别采用密度法、均值法、梯度法选取区间最优收入率,并且将误差范围均设定为[-5%,5%],计算退票率的预测精度,结果见表7,其中使用梯度法得到的退票率预测准确度最高。

表7 不同区间最优退票率选取方法的退票率预测精度对比

4 结束语

铁路部门一直致力于以旅客服务为核心的研究,为充分实现票尽其用,本文以退票率为目标变量进行了分类及预测的研究,旨在能通过预知退票率信息对退票释放的席位进行提前规划。文中分析了退票率数据的特征,提出EW-DBSCAN算法对目标变量进行离散化处理；通过梯度算法获取目标区段内的最优值,在预售期内可以供旅客购票进行参考；通过基于贝叶斯参数优化的XGBoost算法对退票率进行分类及预测,并验证了算法的有效性。后续的研究中可以细化特征变量,研究具体特征对退票率的影响,如研究开车时间与退票率的关系,铁路部门可以将退票率很大的列车通过调整开行时刻等策略来提高运营收益,充分利用现有的运能,满足旅客乘车需求。