铁路运营物资区域联合储备中心选址

田 源，杨 莹，李伊松，施先亮

（1.北京交通大学 经济管理学院，北京 100044；2.北京交通大学 法学院，北京 100044）

1 引言

区域联合储备是基于联合储备中心的各参与主体间权利、责任、风险共担的库存管理模式。依托参与主体间的地域及资源优势，实施共性物资的联合储备，一方面通过减少重复储备，有效降低库存水平，节省仓储费用；另一方面，通过资源整合，有助于促进整体库存管理水平的提升。而区域储备中心选址是联合储备管理中的重要战略决策之一，合理的选址规划不仅关系到资源统筹、效益最大化等目标的实现，也关系到供应的准时性问题。在铁路物资管理的背景下，由于铁路运营物资具有品类多、库存大的特点，且各铁路局之间存在地域差异及管理差异等问题，所以在其运营物资联合储备中心选址问题中进行合理的区域划分及储备中心选址至关重要，成功的选址规划将会带来资金、人力、土地等方面资源的节省，有效提升经济效益。

2 文献综述

以下将从物资联合储备管理及储备中心选址两方面进行综述。一方面，目前针对联合储备管理问题的研究较为丰富，且较多基于企业管理实践的研究，如崔巍[1]在石化企业采购和储备管理中引入了区域协同采购、区域联合储备及JIT的管理理念。张淼[2]研究指出联合储备库存管理模式可以在保证安全生产的基础上，优化库存资源配置，减小库存资金占有，提高资金周转率。安莉[3]、陈谦，等[4]分别针对电网企业和核电厂的联合储备管理问题进行了研究，并用实例说明联合储备所带来的好处。王科清，等[5]研究指出联合储备管理的优势在于能够提高突发事件下的电网事故应急处理效率，缩短恢复供电时间，减少停电损失，提高管理水平。另一方面，目前有关储备中心、配送中心选址的研究已经较为成熟，而聚类思想在选址问题研究中也是一种比较常用的方法。其主要思路是基于相似度的思想将客户点聚类成客户群，从而划分成多个配送区域问题。例如，秦固[6]、Liu[7]等人均是将客户点进行聚类，从而将多配送中心选址问题简化为若干个单配送中心选址问题。陈磊，等[8]、孔继利等[9]则基于模糊聚类的思想构建指标体系，从而实现备选配送中心的划分，然后将问题转化为区域内配送中心选址问题。除去上述方法，k-means作为一种经典的聚类方法，也在选址问题研究中得到了广泛应用。王信波，等[10]、L，等[11]和王云婷，等[12]均采用k-means聚类方法并结合其他选址方法研究配送中心的选址问题。

综上所述，虽然目前针对储备中心选址问题的研究较为丰富，但针对铁路物资管理及联合储备中心选址的研究较少，所以本文为实现我国铁路物资管理资源统筹共享的目标，针对区域联合储备中心选址问题，首先基于改进的k-means聚类算法对区域进行划分，确定配送区域的范围及成员组成，其次通过多目标选址模型在划分完成的区域内选择合适的组织单位负责联合储备的物资管理及存储问题，实现储备中心的选址。

3 基于k-means的联合储备区域划分

3.1 改进K-means聚类算法

k-means算法是较经典且应用范围比较广泛的聚类分析方法，被广泛的应用于配送网络中的配送区域划分分析中，其聚类的目标是尽可能的使各聚类中的末端点相互紧凑，并尽可能使各聚类间相互分开。其优点是可以高效的处理大数据集，且可以得到很好的聚类效果。但考虑到传统k-means算法对初始聚类中心的选取比较敏感，中心选取不当会大大影响聚类结果，以及算法易受噪声和孤立点影响的事实，鉴于此，本文将引入密度思想对传统kmeans算法做如下改进。

3.1.1 引入密度指数。基于密度思想并引入密度指数来确定k个聚类中心，按照从大到小的顺序排列，选取前k个数据点作为聚类中心。其中密度指数的确定方法如下：计算每个数据点Xi的密度(其中i代表数据点的个数，i=1，2，…，n)，R为该点邻域半径当i取某一数值，j=1,2，…，n，Pi代表Xi的密度指数，表达式如下：

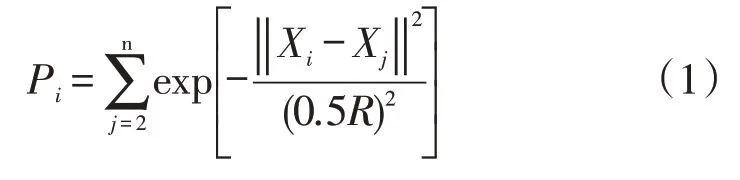
3.1.2 定义相似度。传统算法中用两点之间的空间距离来定义两点相似度的方法，显然在本文的应用背景下是不可取的，为了更科学的衡量铁路局在物资管理方面的相似性及进行联合储备时距离的可行性，本文借鉴城市经济引力模型，以联合采购的物资采购额作为衡量铁路局的经济引力因子，交通运输时间作为衡量物资调拨难易程度的距离因子。则重新定义的距离因子d(Xi-Xj)计算公式如下：

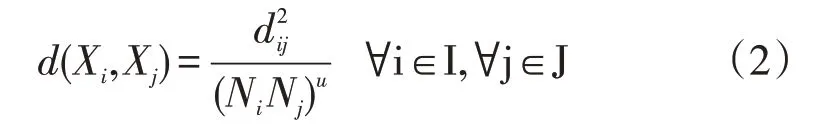
其中Ni,Nj分别代表铁路局i和铁路局j的联合采购物资采购额，由于进行联合储备的前提是各铁路局之间的物资需求量相当，且物资采购需求大的铁路局说明其综合实力更强，所以联采物资总额是衡量铁路局联合储备适应度的重要指标。dij为铁路局i和铁路局j的交通距离，本文以车辆在两座城市之间行驶一趟的交通时间来衡量。u作为调节物流网络划分时受联储物资需求特性的影响程度。一般来说，u越大，则说明在区域物流网络划分时，各铁路局的联储物资需求量的吸引力占主导地位，同时距离因素被一定程度弱化。反之u越小，则距离的影响程度更大，而u=0时，距离即为欧式距离。

3.1.3 确定聚类数目。由于k-means算法的聚类结果受k值的影响较大，所以为提高聚类结果精度，本文采用迭代的方法对k值进行选取。通过计算类别内的组内平方和的评估方法对k值进行筛选，计算公式如下：

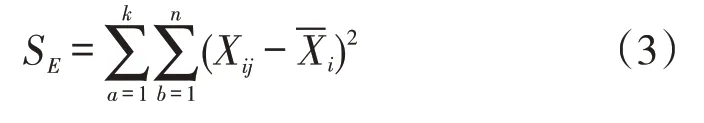
其中式（3）代表组内平方和，即样本点与各自聚类中心的距离平方之和，值越小则代表总的聚类距离越小，聚类效果越好；反之值越大，聚类距离越大，聚类效果越差。用组内平方和的方法确定最佳聚类个数，以达到更好的聚类效果。

3.2 改进k-means算法计算步骤

改进的k-means算法的实现步骤如下：

（1）首先，对数据进行归一化处理。

（2）按照式（1）计算密度指数并按从大到小排列。

（3）取前k个候选点作为聚类中心，按照式（2）计算当k取不同值时的相似度。

（4）计算种聚类结果的组内平方和，选取最优k值，确定最佳聚类方案。

4 区域内联合储备中心选址

4.1 问题分析

在进行铁路物资联合储备区域划分的基础上，现需在各个联合储备区域内选择一个或多个铁路局进行联合储备物资的存储及管理，所以需要对物资的储备地点进行选择。而由于铁路物资需求特性，该选址问题具有以下特点：首先，联合储备中心的地理位置对物资供应的保障程度至关重要，且同时要尽量减少总的物资配送与调拨成本；其次，由于铁路物资种类繁多，仅仅根据一类物资的最优方案来确定储备中心位置显然不合理，所以需要同时考虑多类物资；再者，由于联储物资通常具备价值高，体量大，所需存储空间大，对存储环境要求较高，需要认真选择备选点。

4.2 选址原则

（2）适应性原则。铁路物资联合储备中心的选址应与国家以及地方政府的经济发展规划、大政方针、经济政策相适应，与物流资源分布和需求分布相适应，与当地经济发展和社会发展相适应。

（3）协调性原则。铁路物资联合储备中心选址应将铁路仓储网络作为一个整体进行系统的考虑，使仓库选址有利于其他资源的利用，共同产生更大的经济效益。

（4）保证供应原则。储备中心的最大储备量应满足其所服务半径内所有需求点的需求，正常情况下，区域内供应原则是就近供应，但当面临就近储备中心无法满足需求，或同时出现两个需求点在同一储备点服务半径内需要供应，或发生特别重大事故等特殊情况时，就需要其他储备中心的联合供应以及时满足需求，从而保证铁路正常运营。

4.3 选址目标

（1）目标1-保障供应。考虑到铁路行业对物资需求的特殊要求，在进行联合储备中心选址时不能以牺牲供应及时性为代价，所以联储中心需要在各需求点所期望的时间范围内将物资送达。

（2）目标2-成本最小。铁路物资联合储备的目的就是通过资源整合与共享，降低整体存储规模，从而降低各铁路局及铁路物资管理总成本并提高资源利用率。

4.4 双目标选址模型构建

在进行选址原则及目标分析的基础上，联合储备模式下储备中心选址模型简述如下：

4.4.1 成本最小目标。联合储备中心选址的主要目的是减小物流成本，而运输成本一方面在物流成本中占绝大比例，另一方面由分散储备管理模式转为联合储备主要对运输成本的影响最大，所以除考虑存储成本及订货成本外，运输成本也作为成本因素的重要考量，总成本计算结果如下：

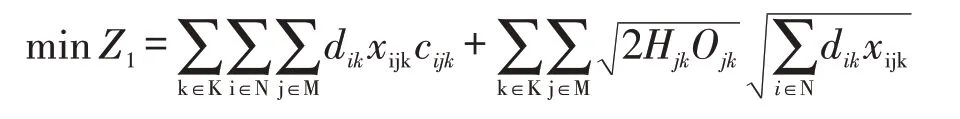
其中N：代表需求点集合，N={1，2，…，n}；M：代表储备中心备选点集，M={1，2，…，m}；K：代表物资种类集合，K={1，2，…，k}；dik：代表需求点i对物资k的平均需求量(件/天)；cijk：代表第j个储备中心向第i个需求点供应第k种物资的单位运输成本(元/件)；Hjk：备选点j对物资k在单位时间内单位物资的存储费用（元/件天）；Ojk：备选点j对物资k的订货费用（元），此费用为常量，在每次订货时发生，并与订货量无关；xijk为0-1变量，当第j个储备中心向第i个需求点供应第k种物资时为1，否则为0。

4.4.2 时间满意度最大目标。铁路行业与一般的交通运输企业不同，铁路运营物资的供应中断所带来的风险不可估计，对于时间敏感度较大的物资来说，供应中断轻则会影响列车的正常运行，重则会产生运行安全问题，所以铁路行业的第一要务就是保证运营物资供应的及时性，由此看出铁路运营物资是时间敏感度较高的物资。所以及时保量的供应是铁路物资储备中心选址所不可忽略的目标和原则。

六是实施技术引领方略，提高水资源的可用性。开源方面，积极发展海水淡化技术、雨水利用技术及替代性水源开发技术；再利用方面，提升污水处理技术、中水回用技术、生物技术水平；节流方面，加强节水设备研发、规范产业节水管理技术，应用节水评价技术；科技支撑体系方面，建立水沙监测与预测预报体系，完善水资源监控体系，建立水安全预警系统等。

因此需求点对于储备中心物资供应的迟到要给予一定惩罚，需要结合惩罚函数的思想将时间延迟造成的成本损失定量表达，时间惩罚成本函数有很多表现形式，一般需要结合具体情况进行选取。

（1）时间满意度函数选取。目前研究中常用的时间满意度函数主要有以下5种。下面通过分析各类满意度函数的适用条件(见表1)，从而找出适合本文研究背景的时间满意度函数。

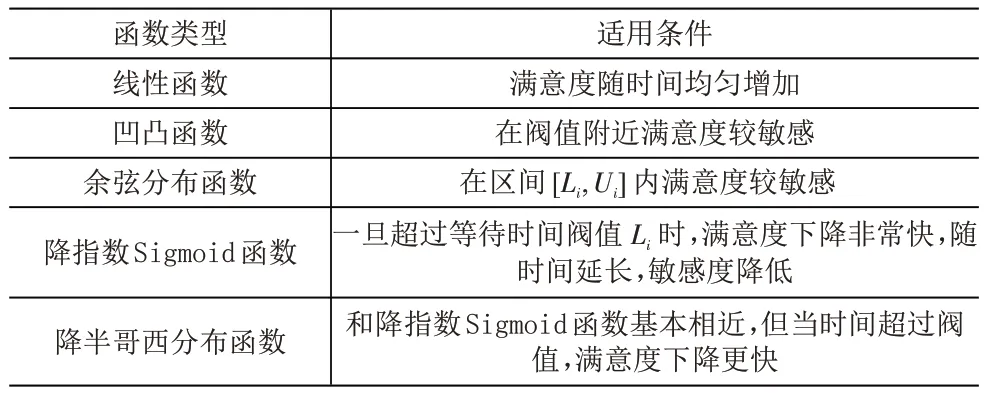
表1 时间满意度类型及适用条件分析

（2）铁路物资供应时间惩罚成本。由于铁路运营物资对于供应及时性要求较高，一旦超过约定时间，短时期内满意度将会迅速下降产生较高的惩罚成本，所以降半哥西分布时间满意度函数最适合本文的研究背景，本文将采用此函数来构造时间惩罚成本函数，降半哥西分布时间满意度函数图像如图1所示。

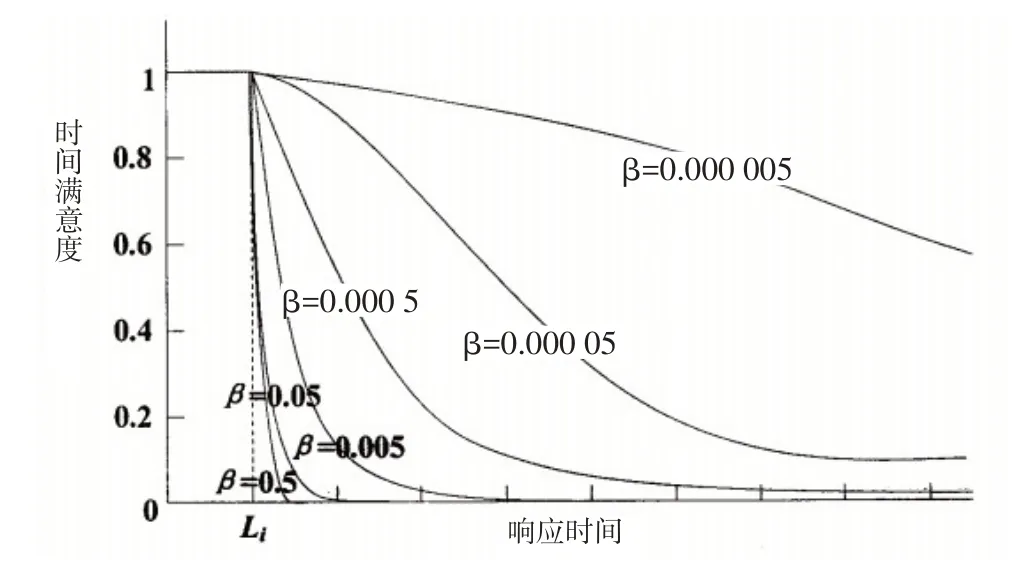
图1 降半哥西分布时间满意度函数图像

可以看出时间满意度函数中自变量和因变量呈反向变化，等待时间越长需求点的时间满意度水平越低，而时间惩罚成本与等待时间成同向变化，即等待时间越长，供给点应该付出的惩罚成本越多。用时间满意度水平的倒数来构造时间惩罚成本函数，通过降半哥西分布时间满意度函数可得：

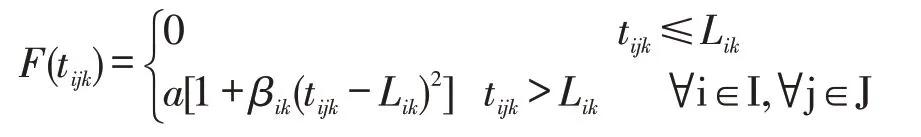
其中，F(tijk)：需求点i向供给点j供给物资k的时间惩罚成本；a：单位时间惩罚成本；βik：需求点i对物资k的时间敏感系数；tijk：需求点i接受供给点j提供物资k的最短等待时间；Lik：需求点i感到满意度下降的临界点，即愿意等待的最长时间。

4.4.3 双目标选址模型

式（4）代表总运输、储存及订货成本；式（5）代表时间惩罚成本；式（6）表示一个需求点只能由一个储备中心供应；式（7）表示储备中心发生供应是其被选择为前提；式（8）表示选取的储备中心数量小于阈值；式（9）—式（11）为0-1变量。

5 实证分析

5.1 问题背景及数据获取

目前，我国铁路运营物资库存管理均以铁路局集团公司为单位开展，物资储备分散管理会导致各贮存点之间调配难度大，闲置物资比重高，以及为了保障生产供应，每个贮存点的储备库存体量通常偏大，导致重复储备库存占用资金过高。所以，结合铁路建设与运营点多、线长、面广的特点，同一线路固定设备基本相同、配件基本通用的特点，选择部分共性强且易于调配的物资进行跨铁路局集团公司联合储备，通过区域划分+区域内储备中心选址的方法进行联合储备实施。

本文通过收集我国18个铁路局集团公司联合采购物资采购总额，以及相互之间的交通运输距离及时间，并对数据进行了归一化处理消除数据量纲影响。其中，18 个铁路局分别为北京局、太原局、呼和浩特局、沈阳局、哈尔滨局、上海局、济南局、南昌局、武汉局、郑州局、广州局、成都局、昆明局、南宁局、西安局、兰州局、乌鲁木齐局、青藏局。

5.2 改进方法选址求解

5.2.1 联合储备区域划分

（1）确定聚类中心候选点。首先对18 个铁路局的密度指数进行计算，选取排名前8的铁路局作为聚类中心首选，分别为沈阳、北京、武汉、西安、上海、广州、成都、太原。

（2）确定聚类数目。分别选取聚类数目为3-8，并计算每种聚类结果的组内平方和进行聚类效果评估，组内平方和随聚类数目变化的曲线图如图2所示，从图中可以明显看出，当聚类数目k=6 时的组内平方和值最小，所以此时聚类效果最好，实现组内相似性高且组间差异性大的聚类效果。

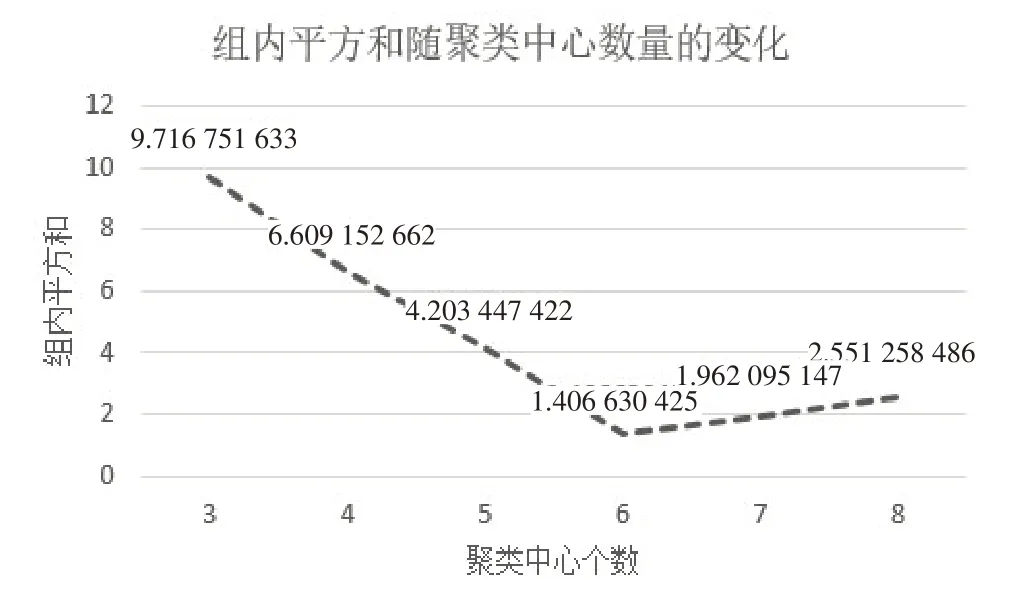
图2 组内平方和随聚类中心数量的变化

（3）聚类结果。确定最佳聚类个数后，根据改进的k-means 算法聚类，当k=6 时，聚类结果如图3所示，具体见表2。

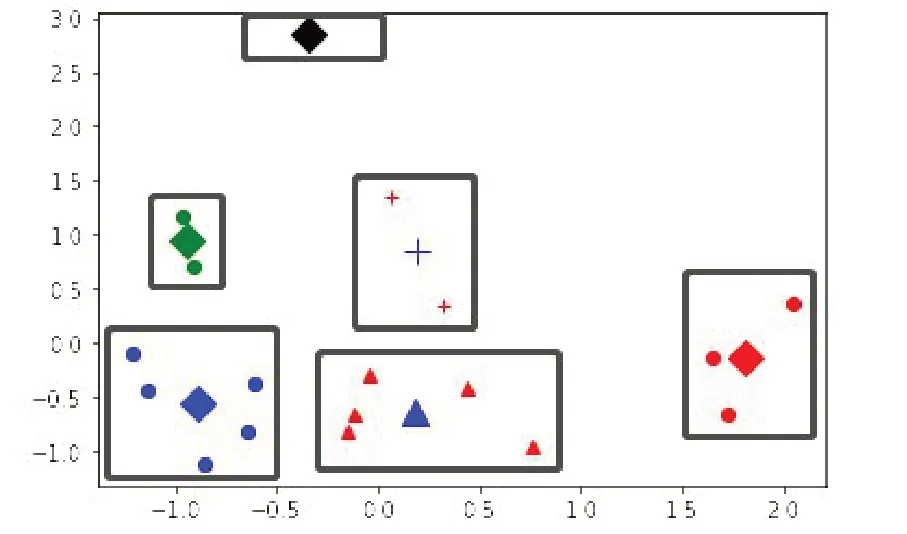
图3 k=6时聚类结果

表2 k=6时聚类结果

5.2.2 区域内储备中心选址

（1）参数设置。在得到区域划分结果的基础上，将继续对各区域进行储备中心选址，本文以机车车辆配件联储为例（共分为6 类，见表3，所以k=6）；单位时间惩罚成本a=300，cijk=ck代表运输物资k 的单位运输成本。

表3 铁路机车车辆配件类别

假设所有需求点对同类物资的需求敏感系数相同(见表4)，所能接受的最长等待时间因物资需求计划提报的差异性而有所不同，每个区域内符合设置储备中心备选点条件的铁路局数目见表5。

表4 物资需求敏感系数

表5 联合储备区域内储备中心备选点选择

（2）选址结果。本文运用matlab 对选址模型进行求解，由于区域1、4、6 符合条件的备选点只有一个，所以可直接得出结论。经过对其他3个区域逐一选址，得到选址计算结果（见表6），其中Z=Z1+Z2代表总成本。

通过对各区域内的计算结果比较，选取总成本最小的备选点作为最终储备中心的选址位置，则选址结果见表7。通过将选址结果与聚类结果比较可以发现，聚类中心与最终的储备中心选址结果只在少数区域有所不同，由于聚类分析中参数u=0.1，将物资需求相似性相对于距离因素对最终聚类结果的影响进行弱化，所以结合选址结果可以发现，若在空间分布上处于区域中心位置，并具有物资储备及管理能力的铁路局将会被选择为区域联合储备中心的选址地点。

表6 储备中心选址计算结果

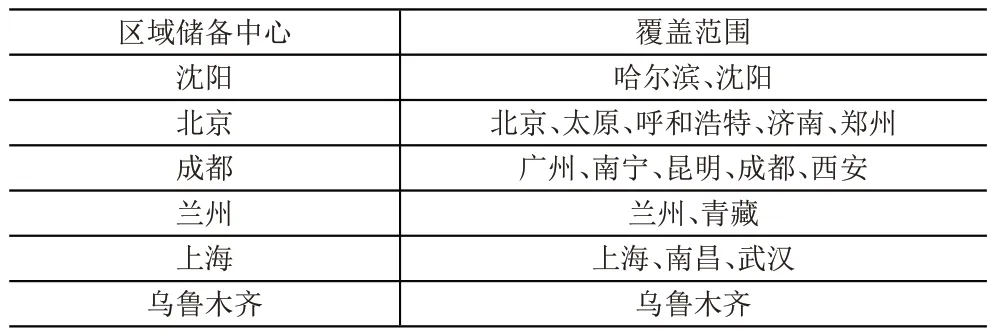
表7 区域储备中心选址结果

6 结论

通过本文分析得到如下结论：基于问题背景对区域划分及选址因素进行考虑，更能切实有效的解决问题。本文在铁路物资联合储备管理的背景下，通过将距离因素与联合采购额指标相结合对聚类方法的相似度进行衡量，对k-means 算法进行了改进。并基于铁路物资需求需要保证供应的特点，构建了基于成本最小及保证供应的双目标选址模型，并基于我国18 个铁路局的实际数据，验证了模型的有效性并实现了铁路运营物资联合储备区域划分及储备中心选址，可为铁路物资管理决策提供理论借鉴。但本文考虑的实际因素仍然有限，需要在以后的研究中结合实际因素对模型不断修正，提高模型的精准性与实用性。