基于MDP-GERT的航空装备维修保障流程优化研究

2019-12-31郭之俊王瑛孙贇李超

航空工程进展 2019年6期

郭之俊，王瑛，孙贇，李超

(空军工程大学装备管理与无人机工程学院，西安 710051)

0 引言

随着信息化战争向着多维一体、快速打击等目标的不断推进，以及高新技术在武器装备上的广泛应用，对航空装备维修保障的要求日益增高。维修保障作业时间作为制约战场上军机再次出动能力的重要指标，关系着战斗力的快速生成。然而，在战时的航空装备维修保障中，往往存在着有限的维修保障能力难以同时满足多架军机保障需求的矛盾。为在一定的维修保障能力下，尽可能缩短维修保障时间，提高维修保障效率，对航空装备维修保障流程优化进行研究十分必要。目前，国内外对装备保障流程优化的研究较为关注，使用较多的研究方法包括整数规划[1]、多目标优化[2]、Petri网仿真[3]、随机网络技术[4]等多种方法。在众多方法中，图示评审技术(Graphical Evaluation Review Techonology，简称GERT)可以很好地刻画保障活动时间服从随机分布的情况及活动间的逻辑关系，故广泛应用于维修保障流程的建模仿真中。邓堃等[5]利用GERTS对具有较强资源依赖性的维修过程进行了描述，并给出相应的资源配置方案；张建强等[6]利用Q-GERT仿真了航空装备维修保障流程中排队过程，分析了任务完成率等指标；吴勇等[7]利用GERT网络对舰载机保障流程模型进行求解，据此给出了相关的决策建议。上述模型主要侧重于通过计算相关指标以提供流程优化的决策支持，而不能直接对保障流程进行优化排序。

与此同时，马尔科夫决策过程(Markov Decision Process，简称MDP)作为一类研究随机序贯决策的理论，可以有效地处理系统的动态调度和流程优化问题，F.Pedberg[8]首先提出了一种基于马尔科夫过程的进度计划方法；齐婷婷[9]应用马尔科夫决策过程理论，对IT项目开发进度计划进行了优化；张学杰[10]讨论了马氏决策规划在战时装备维修中的应用。但是，上述研究在进度计划时，只考虑对任务时间确定时的情况，因而无法描述现实中任务时间的随机性，影响了优化结果的精确计算。

为了对保障流程进行优化排序，本文建立一种嵌入马尔科夫决策过程的GERT模型，首先通过添加决策节点、构建最优维修策略下的GERT网络，以描述装备维修保障流程；然后基于策略改进法和蒙特卡罗方法，提出该模型的求解算法；最后结合案例，应用模型对多架飞机的维修保障流程进行优化排序和灵敏度分析。

1 装备维修保障流程优化模型构建

航空装备维修保障活动是由许多相关操作活动彼此按逻辑顺序关联而成的一种系统活动，具有工序多、流程复杂等特点，使用网络图可以较好地表达各项活动的优先级和相互作用，而流程优化问题实质是一种序贯决策求全局最优的问题，故这里尝试在GERT网络中嵌入决策节点，构建MDP-GERT网络模型。

在航空装备维修保障流程中，可以将某些重要事件作为标志，将维修保障流程划分为若干个阶段，保障活动在每个阶段可能处在不同的状态，各阶段之间的状态按照一定的概率和参数转移，由此构建航空装备维修保障流程MDP-GERT网络模型基本单元，如图1所示。

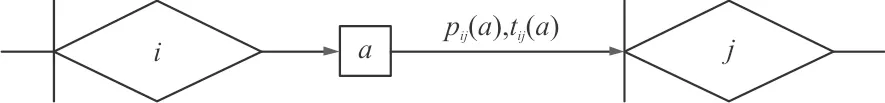
图1 MDP-GERT网络模型基本构成单元示意图

Fig.1 Schematic diagram of basic components of

MDP-GERT network model

定义1MDP-GERT网络模型基本构成单元。如果使用异或型节点表示维修保障流程中的某个阶段内保障活动所处的状态，正方形节点表示在该阶段决策者采取的决策，正方形节点和异或型节点之间的箭线表示采取某一决策的情况下阶段之间的转移情况，那么，对于任意一个维修保障流程，其MDP-GERT网络模型可以用以下五元组{S,A(i),tij(a),pij(a),V}表示。其中：

S={s1,s2,…,sn}表示维修保障流程中所有可能出现的保障活动所组成的非空有限集合；

A(i)={ai1,ai2,…,aim|i∈S}表示在状态i后，决策者可用的决策集合，一般在实际维修保障流程中往往是非空有限的；

tij,pij(a)分别表示在当维修保障流程处于状态i之后并且采用决策a时，维修保障流程阶段转移到状态j过程的花费时间和概率。

V为目标函数，表示在一定策略π下从起始状态出发到终止状态时获得的总传递变量期望。

在每一个阶段下，由于GERT网络具有马尔科夫性，显然决策的做出依赖于当前的维修保障状态，与之前的历史无关，而在维修保障流程中，每一阶段的决策都是一种确定选择而非以一定概率的选择，故可以用随机马氏策略π={a1,a2,…,an}表示整个维修保障流程中的决策序列。那么，目标函数V表示在一定策略π下从起始状态出发到终止状态时获得的总传递变量期望。

为便于对维修保障流程进行优化，根据GERT网络模型传递参数与矩母函数的关系，给出以下定义：

定义2MDP-GERT网络模型传递函数。在某一策略π下，随机网络的参数传递函数为

(1)

(2)

式中：pik为在采用决策a时，状态i到状态k的状态转移概率；Mik(s,a)为此时的活动参数服从的随机变量的矩母函数。

定义3MDP-GERT网络模型报酬函数。若维修保障流程处于状态i之后并且采用决策a时，则这里由(i,a)所决定的维修保障流程下一阶段所需花费的时间T(i,a)可被称为MDP-GERT网络模型报酬函数。

定义4MDP-GERT网络模型目标函数。在策略π下，由初始状态i出发的期望总报酬作为最优策略的比较目标，以Yn,Dn分别代表在n阶段维修保障流程所处的状态和将采取决策，则

(3)

目标函数(或称为准则函数)V是寻找项目最优决策的函数，是各阶段期望报酬的和。目标函数可以由式(4)表示

(4)

在这里需要说明，由于维修保障流程优化中的目标是维修效率最高，或者说总维修时间最短，故决策带来的并非“报酬”而是耗费的时间，相当于“费用”，这样在计算时将所有ti(a)加上负号，最终就可以得到相同的结果。

2 装备维修保障流程优化模型求解

2.1 MDP-GERT网络模型的简化

根据信号流图的拓扑等价性质，如果存在自环，可以对阶段内的网络模型按式(5)进行化简，使之成为等价的单箭头网络模型，如图2所示。

(5)

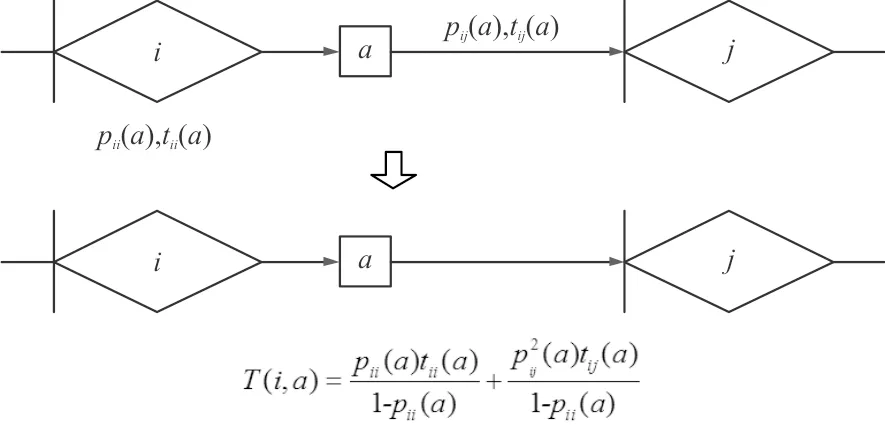
图2 MDP-GERT网络模型中自环结构的等价转化Fig.2 Equivalent transformation of self-loop structure in MDP-GERT network model

这里根据定义2和信号流图的等效转换关系，由于采取决策a后所有可能的ti(a)间为并联关系，可以对阶段内的网络按公式(6)进行化简，使之成为等价的单箭头网络模型，如图3所示。

T(i,a)=∑pi(a)ti(a)

(6)

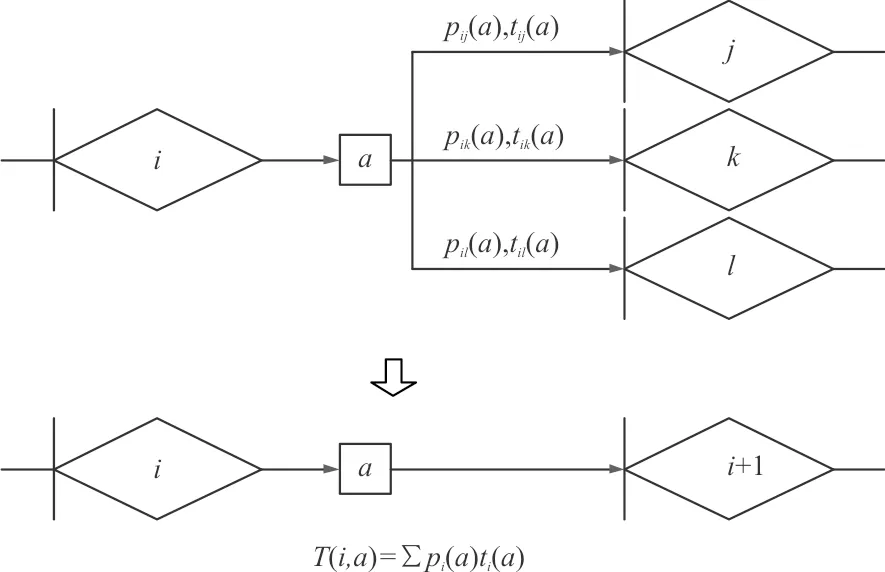
图3 MDP-GERT网络模型中并联结构的等价转化Fig.3 Equivalent transformation of parallel structure in MDP-GERT network model

在某一策略下，在每一阶段后只能选择一种决策，这意味着在这种情况下，只有被采取的决策后的箭线上的参数有意义[11-12]，没有被选择的决策点后的网络部分需要被剪枝，如图4所示，传递函数恒为0。

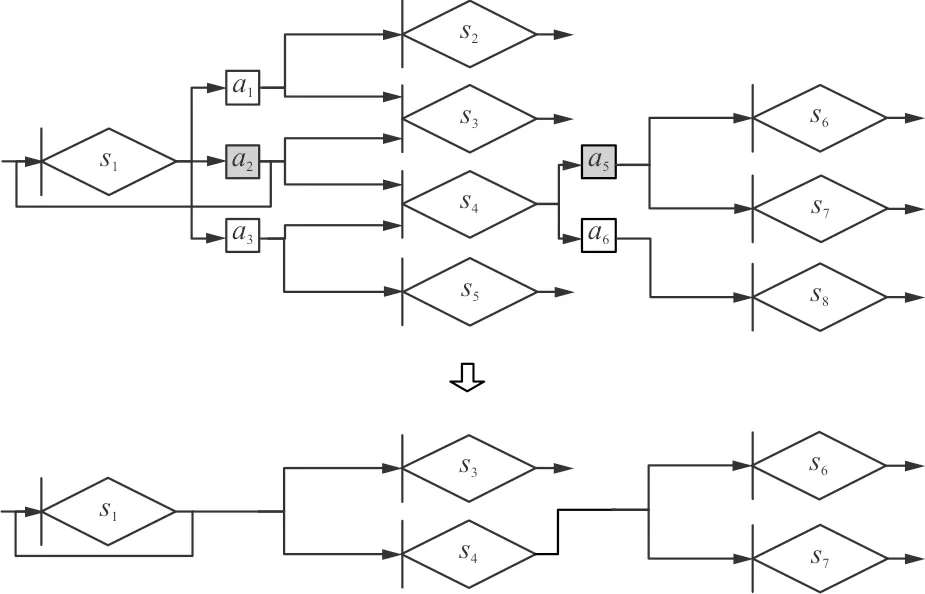
图4 在某一策略下MDP-GERT网络模型时的等价转化Fig.4 Equivalent transformation of MDP-GERT network model under a certain strategy

2.2 航空装备维修保障流程最优策略求解

通常使用德尔菲法获得保障流程中各单项活动的概率分布类型和数字特征。由于每次决策都会带来网络的结构调整，使用矩母函数求解最优策略具有相当大的困难，故这里直接利用各活动时间的期望进行策略寻优，对于MDP过程采取策略迭代法进行迭代，步骤如下：

Step1初始化：令初值V(i,a)=0，中间变量c1=c2=0；

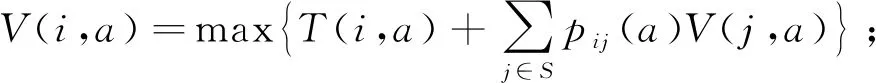
Step3计算边界值：

c2=|V(i,a)-c1|

Step4进行比较：当c2<ε时，输出最优策略π，否则重新进入Step2进行迭代。

当t≤0时，V(i,a)满足策略迭代法寻优的收敛条件[13]。

2.3 最优策略下的维修保障流程时间分析

针对利用解析法对航空装备维修保障MDP-GERT网络模型求解存在网络结构过于复杂，只能得到参数的期望而不能得到各参数的准确概率分布等问题，考虑运用蒙特卡罗仿真模拟的方法来对最优策略下的维修保障流程时间进行分析。蒙特卡罗方法求解GERT网络一般可分为邻接矩阵法和简化递推法。邻接矩阵法的思路是分解网络成后利用已知各状态间的转移概率，随机地对某一子网络进行模拟计算，经过若干次的模拟后，统计各子网络实现次数和参数的特征值，得出模拟结果。采用简化递推法先对GERT网络进行简化，当网络通过等价变换逐步简化、综合成一个确定型网络后，再进行模拟计算。邻接矩阵法仅适用于结构不是很复杂且不包含环路的GERT网络，在这里选择简化递推法，其中网络中非自环需要先被转化为自环。转化公式如下：

(7)

(8)

网络中非自环被转化为自环之后，还需要判断网络中的串并联情况和自环情况，如果存在自环则还需要将其消除直至网络被转化成为一个确定型网络。为了方便利用计算机求解，可利用矩阵化变换解析方法[14]对网络进行消除自环和节点的操作。

总结上述过程，航空装备维修保障流程MDP-GERT网络模型的建模和求解可按照以下步骤进行。

Step1根据实际问题的背景和系统的基本特征，利用德尔菲法获得各单项活动的传递参量，构造航空装备维修保障流程MDP-GERT网络模型；

Step2根据网络中每项活动的基本参量，按照定义2和定义3，确定每项活动的报酬函数及整个项目的目标函数，利用策略迭代法求解最优随机马氏策略π；

Step3对最优策略π下的网络进行剪枝；

Step4利用蒙特卡罗模拟方法对最优策略π下的航空装备维修保障流程MDP-GERT网络模型进行求解，得到最优策略π下的维修项目进度的时间分布。

Step5根据结果结合实际情况对航空装备维修保障流程进行分析，对单项项目参数进行优化改善，便于进一步缩短维修保障流程，提高装备维修保障能力。

3 案例分析

选取三架不同型号飞机在战时需要进行快速充氮的情境为例，说明本文提出的建模和求解方法的使用。根据工作分解结构(Work Breakdown Structure，简称WBS)原理[15]，该航空装备分系统的维修保障流程可以分成三个阶段。由于飞机的型号不同，充氮工作的工序稍有区别，充氮设备有限，需要维修保障的管理人员针对不同状态采取决策，决定本阶段对某一飞机型号进行检修。针对该问题，构造其保障流程MDP-GERT网络模型如图5所示，使用德尔菲法，依据相关经验和历史数据，已知相关活动参数如表1所示。

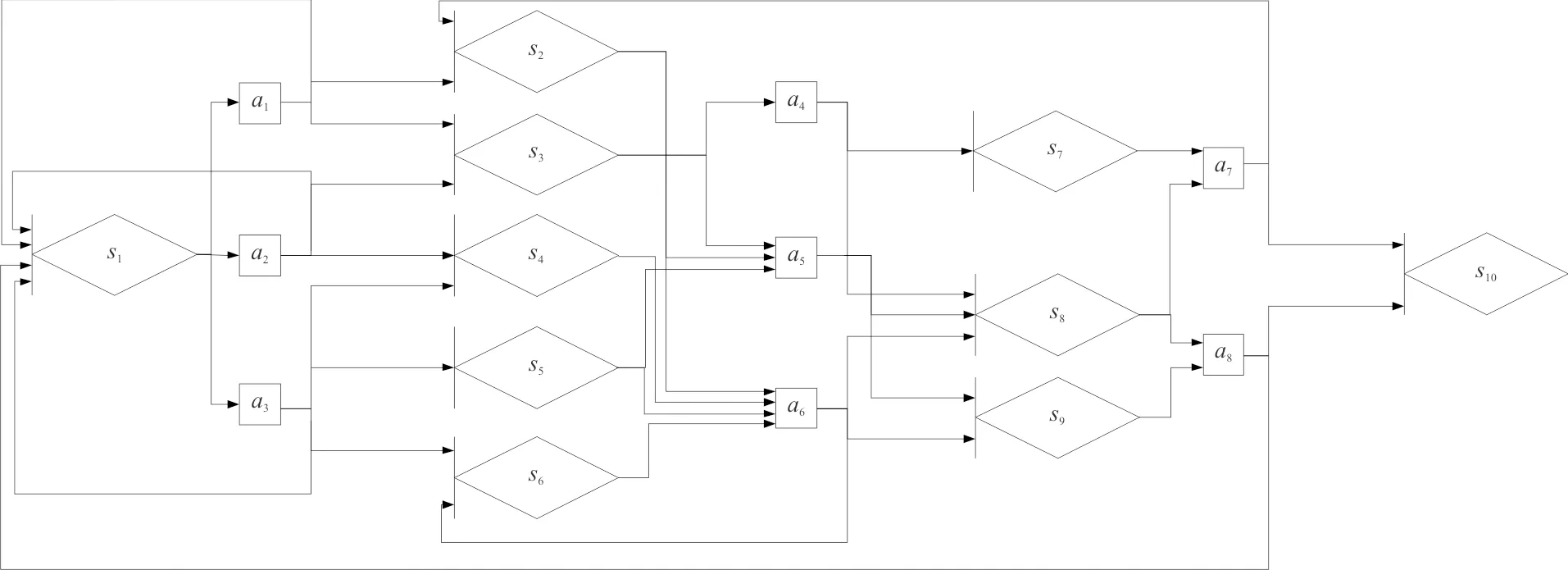
图5 三机战时充氮保障作业MDP-GERT网络模型Fig.5 MDP-GERT network model for nitrogen filling support operation of three aircrafts in wartime

表1 三机战时充氮保障作业各活动参数Table 1 Activity parameters of nitrogen filling support operation of three aircrafts in wartime

为验证模型的决策效果，按照式(3)进行策略迭代计算定义的报酬函数，不考虑其他条件对活动的制约，将部分策略获得进行对比，结果如表2所示，可以看出：决策序列中首先对a3决策所代表的机型进行维修是较为合理的。

表2 部分策略下三机战时充氮保障作业总报酬值Table 2 Total rewards of nitrogen filling guarantee operation in three aircrafts under part of the policy

全部计算结果表明当采取策略5，即π={a3,a5,a8}的决策序列为最优策略。在策略5下对原网络进行化简，化简后网络如图6所示。

图6 最优策略下化简的保障作业MDP-GERT网络模型Fig.6 Simplified MDP-GERT network model of guarantee job under the optimal strategy

网络模型进行蒙特卡罗仿真模拟如图7所示，试验次数设置为20 000次，当作业排序π={a3,a5,a8}时得到三机战时充氮保障作业最优维修时间期望为16.18 min，利用一般的GERT网络对未经优化的充氮保障作业流程进行维修时间估计，得到维修时间期望为22.04 min，优化后保障时间较未优化时缩短了26.59%。

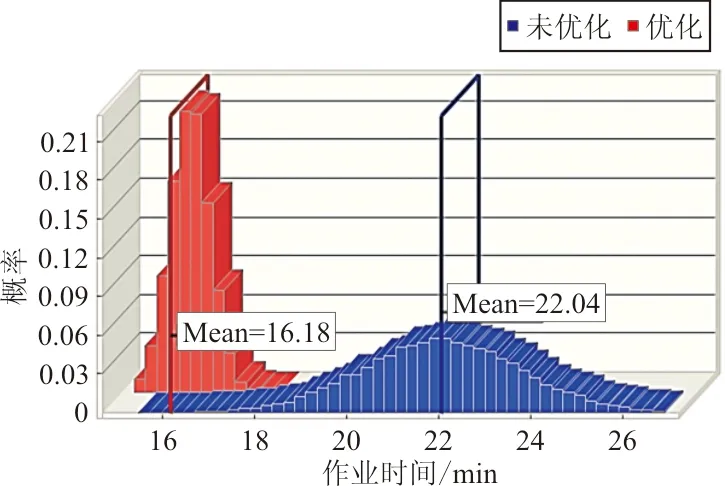
图7 优化前后的三机战时充氮保障作业时间Fig.7 Operation time of nitrogen filling guarantee before and after optimization of three aircrafts in wartime

对流程中各活动时间进行敏感性分析和相关分析，结果如图8～图9所示，可以看出：充氮保障作业流程中活动a3(s1,s5)，即充氮车的及时到位是制约充氮保障作业流程的关键活动，充氮车的到位时间与充氮保障作业的总时间为正相关关系，其影响达到43.1%，事实上，在实际保障作业的优化中，充氮车是否到位直接决定了战场上保障活动能否直接进行，避免等待，因此应该得到着重关注。