水翼型水上飞机偏转机翼布局数值研究

2019-12-31申遂愿朱清华曾嘉楠朱振华王坤

航空工程进展 2019年6期

申遂愿，朱清华，曾嘉楠，朱振华，王坤

(南京航空航天大学直升机旋翼动力学国家级重点实验室，南京 210016)

0 引言

水上飞机兼具飞机与高性能船舶的一些共同特点，能够在水面滑行、起飞与降落，也能在空中飞行，装有起落装置的水上飞机能够在陆地起降[1]。1905年法国航空先驱瓦赞兄弟设计了世界上第一款水上飞机[2]，第二次世界大战后，水上飞机随着航空技术的进步得到迅速发展，可靠性和飞行性能得到很大提高。较为著名的水上飞机有美国LA4-200水陆两栖飞机，其先后生产了1 000多架[1]，日本的US-1型水陆两栖飞机，采用了抑制水上起飞降落水花喷溅的技术，德国的Seastar两栖飞机优化船体设计减小水动阻力，俄罗斯在A-40基础上研制出森林灭火型两栖飞机Be-200[3]。

中国在20世纪70年代研制出水轰-5水上飞机，主要用于反潜与灭火[4]，90年代南京航空航天大学研制出FT300轻型水上飞机，主要用于民用观光旅游、水上缉私等方面[5]；21世纪，航空工业特种飞行器研究所研制的AG-600型水上飞机于2018年完成水面起飞试验，该型水上飞机是目前世界上最大的水上飞机。

传统水上飞机分为单浮筒式、双浮筒式和船身式三种类型。传统型水上飞机水面起飞阻力峰值远高于飞机巡航状态所受阻力，为了满足水面起飞条件而安装大功率发动机，而水上飞机巡航飞行时间远多于水面起飞时间，发动机水面起飞过程短时间输出大功率，大部分时间工作在小转速低输出功率状态，容易对发动机造成损坏，缩短发动机使用寿命[6]。同时，附加的浮筒或船身设计增加了飞机的重量，降低了飞机的有效载荷。

法国Lisa航空公司于2012年设计制造了Akoya水翼型水上飞机，Akoya飞机机身腹部与尾部均安装有水翼，取消了浮筒与船身式设计。水的密度约为空气密度的800倍，因此较小浸水面积的水翼割划水面能产生较大的水动升力，Akoya水上飞机的速度达到一定值后，水翼产生的水动升力将机身抬离水面，从而减小飞机的浸水面积，降低飞机的水动阻力峰值，实现快速短距水面起飞，但该种构型额外的水翼对飞机空中飞行性能产生一定不利影响。

目前针对水翼型水上飞机的研究较少，水翼型水上飞机水面滑行状态与水翼船水面航行状态类似，可以参考其研究方法。水翼船水动性能研究方法主要分为三种：一是通过实验的方法进行研究，如迟云鹏等[7]对30 t槽道水翼滑行艇进行了试验，研究了水翼剖面形状、水翼安装角、船体重心位置等对槽道水翼滑行艇阻力性能的影响；二是通过经验公式和工程方法进行估算，如唐建飞等[8]结合经验公式和简化模型得出了水翼船阻力计算方法；三是基于CFD软件进行水翼船阻力计算，如周进[9]采用SSTk-ε模型对水翼滑行艇阻力与耐波性进行了研究并使用VOF方法对自由液面进行了捕捉。

上述研究方法虽能较准确计算水翼船的水动性能但未考虑空气动力因素影响，而空气动力对水翼型水上飞机水面滑行影响较大，因此本文提出了一种可偏转机翼布局水翼型水上飞机，采用空气动力和水动力耦合求解并结合动力学平衡方程方法对水动性能进行数值研究，该方法综合考虑了空气动力及水动力影响，尽可能准确计算水翼型水上飞机水动性能。

1 水翼型水上飞机偏转机翼布局特点

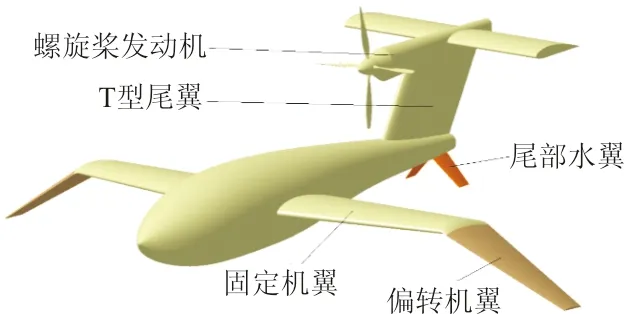
为满足水上飞机水面滑行和空中飞行综合性能的最优化，设计可偏转机翼水翼型水上飞机如图1所示，具体布局特点为：

(1) 水翼型水上飞机机翼分为固定机翼与偏转机翼两部分，固定机翼采用NACA4415翼型，偏转机翼采用SIMPLE9翼型。SIMPLE9翼型为弓背形翼型，压力分布均匀，能有效降低发生空泡的可能性，具有优异的水动性能。

(2) 水翼型水上飞机尾部安装有尾部水翼，尾部水翼采用SIMPLE9翼型。

(3) 尾翼采用常规的T型尾翼设计防止平尾受到机身溅起波浪的影响，螺旋桨发动机安装在垂尾上。

飞机水面滑行状态如图1(a)所示，偏转机翼偏转至与水平面呈30°角，当飞机速度达到一定值，偏转机翼与尾部水翼产生的水动升力将机身抬离水面减小飞机水动阻力。飞机离水起飞后，如图1(b)所示，偏转机翼偏转至与水平面水平，此时机翼能够提供更大的升力。飞机静止在水中时水线位置图如图1(c)所示，其中深色部分为飞机浸在水中部分。

(a) 水面滑行状态

(b) 空中飞行状态

2 水动特性分析

2.1 水动力计算方法

水面起飞过程比陆地起飞过程更加复杂，首先需要考虑水面波浪对其飞行姿态的影响，其次除了空气动力与发动机推力大小及方向的影响，还存在不断变化的水动力与重力的作用[6]。若直接对水上飞机进行数值模拟，由于水上飞机对水面与空气两种介质的网格与边界条件要求不同，存在计算不兼容的问题，计算时间长且计算精度较低[3]。因此需要将空气动力与水动力分别求解，再通过动力学方程将两者结合修正水上飞机飞行参数，其具体计算流程如图2所示，首先给定一个初始飞行条件如飞行速度、飞机俯仰角、发动机推力与方向等，分别计算该状态下水动力与空气动力，通过动力学平衡方程修正飞机飞行姿态，同时改变水线高度，迭代计算直至飞机达到平衡条件，得到该平衡条件下飞机的水动特性。空气动力计算模型不包括后段偏转机翼与尾部水翼，水动力计算模型只包含飞机机身、机翼与尾部水翼，其动力学平衡方程[10]为

水平方向：

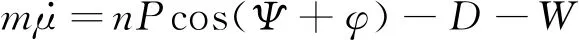
(1)

竖直方向：

mg=Lw+La+T-nPsin(Ψ+φ)

(2)

绕重心转动：

Lqsx1+Lhsx2+Lax3=0

(3)

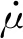
图2 水面滑行计算流程图Fig.2 Flow chart for calculation during surface taxiing

2.2 水动力计算方法验证

由于水翼型水上飞机贴近水面起飞，因此进行空气动力计算时需要考虑地面效应对其气动性能的影响，本文选择NACA0012三维地效矩形机翼[11]进行空气动力算例验证，机翼弦长c=400 mm，机翼展长l=800 mm，机翼后缘到地面距离h=40 mm，来流速度V=50 m/s。

数值计算采用Realizablek-ε湍流模型，压力-速度耦合采用SIMPLE算法。计算结果与文献[11]试验结果对比如表1所示，可以看出：升阻系数误差均在5%以内，表明上述计算方法适用于空气动力计算。

对Wigley船型[12]在不同弗汝德数下进行水动力算例验证，Wigley船型方程为

(4)

式中：A为船宽；L为船长；H为吃水深度；0≤x≤L，-H≤z≤0，其中L=2.5 m，A=0.25 m，H=0.156 m。

表1 NACA0012机翼模型试验数据与CFD模拟结果比较Table 1 Comparison of NACA0012 wing model test data with CFD simulation results

采用RNG 湍流模型进行数值计算，采用VOF方法对自由水面进行捕捉。计算结果与文献[12]试验数据对比结果如表2所示(表中CT1为CFD模拟结果，CT2为试验结果)，可以看出：总阻力系数误差在5%以内，表明上述计算方法适用于水动力计算。

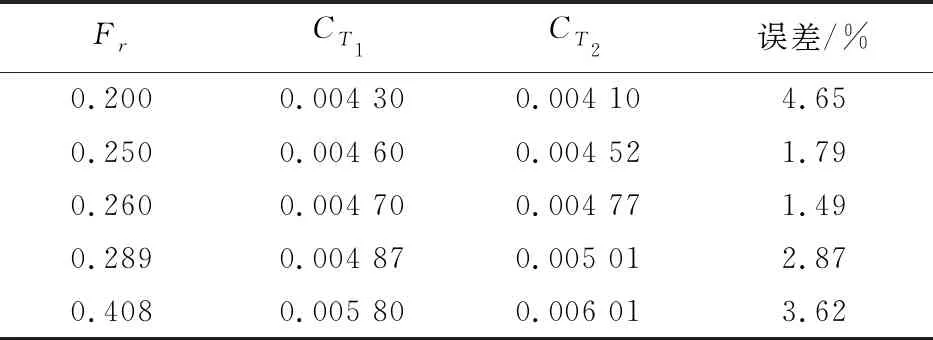
表2 Wigley模型试验数据与CFD模拟结果比较Table 2 Comparison of Wigley model test data with CFD simulation results

2.3 水动性能计算

水翼型水上飞机水面起飞过程中，偏转机翼偏转30°，水动力计算网格如图3(a)所示，其中1代表水，2代表空气，1、2的分界线为飞机水线位置；边界条件设置如图3(b)所示，速度入口分为空气入口和水入口，采用速度入口边界条件，速度大小设置相同，出口为自由出流，底面为移动壁面，对称面为对称边界，飞机为无滑移壁面，其他面均为滑移壁面。水翼型水上飞机速度V=12 m/s时水线位置图如图4所示，水翼型水上飞机自身浮力FT变化曲线图如图5所示。

(a) 水动力计算网格

(b) 边界条件图3 网格及边界条件Fig.3 Mesh and boundary conditions

图4 速度V=12 m/s时水线及水面状态图Fig.4 Water line chart at V=12 m/s

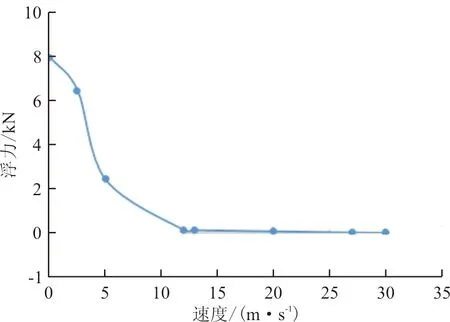
图5 水翼型水上飞机浮力变化曲线图Fig.5 Curve chart of buoyancy of hydrofoil seaplane

从图4～图5可以看出：随着飞机速度的增加，偏转机翼和尾部水翼产生的水动升力随之增大，将飞机机身逐渐抬离水面，飞机浸水部分体积不断减小，从而所受浮力迅速减小；速度V=12 m/s时，飞机的水动升力将机身完全抬离水面，此时只有小部分偏转机翼及尾部水翼在水中，飞机浮力变化缓慢。

水翼型水上飞机总升力随速度变化曲线图如图6所示，可以看出：当水翼型水上飞机速度低于12 m/s时，机身未离开水面，偏转机翼浸水面积较大，因此随着速度的增加，水动升力升高较快，最大水动升力为6 966 N，约占总升力的88.1%，该阶段由于飞机速度较小，空气动力影响不大，当速度超过12 m/s后，机身离开水面，总升力变化不大，偏转机翼浸水面积减小加快，产生的水动升力逐渐减小，而飞机的气动升力逐渐增加，当速度超过24 m/s时，气动升力超过水动升力，当速度达到30 m/s时，水动升力降至0，水翼型水上飞机离开水面。

图6 水翼型水上飞机总升力随速度变化曲线图Fig.6 Curve chart of total lift change with velocity of hydrofoil seaplane

水翼型水上飞机总阻力随速度变化曲线图如图7所示，可以看出：当水翼型水上飞机速度低于12 m/s时，空气阻力增加缓慢，水动阻力急剧增加，阻力主要来源于偏转机翼的水动阻力，最大水动阻力为1 465 N，该阶段随着速度的增加，由于飞机速度较小，水动升力不足以将机身抬离水面，水翼型水上飞机浸水面积较大，水动阻力增加较快；当速度超过12 m/s后，机身离开水面，水动阻力开始下降，空气阻力上升加快，水翼型水上飞机水面起飞过程所受最大阻力为1 511 N。

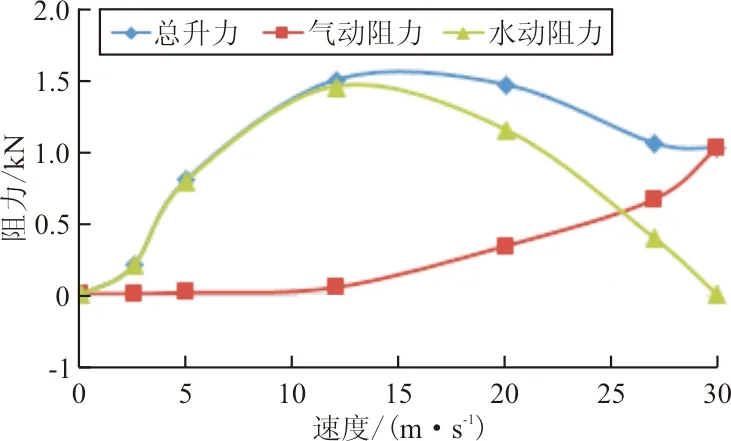
图7 水翼型水上飞机总阻力随速度变化曲线图Fig.7 Curve chart of total drag change with velocity of hydrofoil seaplane

为验证水翼型水上飞机偏转机翼布局的水动性能，选用双浮筒型水上飞机作为参考模型进行对比研究。双浮筒型水上飞机与水翼型水上飞机具有相同的机身和尾翼形状，机翼采用NACA4415翼型，弦长、安装角、水平投影面积与水翼型水上飞机相同，双浮筒水上飞机取消水翼设计，在机身下部安装两个大小形状一致的浮筒，如图8所示。双浮筒型水上飞机依靠浮筒在水面滑行，在水面漂浮时两个浮筒承受了飞机的全部重量。

图8 双浮筒型水上飞机计算模型Fig.8 Computational model of double-float seaplane

采用与水翼型水上飞机相同数值模拟方法对双浮筒型水上飞机进行计算。两种构型浮力随速度变化曲线图如图9所示。

图9 两种构型浮力随速度变化曲线图Fig.9 Buoyancy vs velocity for two configurations

从图9可以看出：随着速度的增加，飞机浸水体积在逐渐减小，水翼型水上飞机浸水体积减小速率快于双浮筒型水上飞机，因为水翼产生的水动升力要远远大于浮筒产生的水动升力，当水翼型水上飞机机身离开水面后，飞机自身浮力较小。两种构型总阻力随速度变化曲线图如图10所示。

图10 两种构型总阻力随速度变化曲线图Fig.10 Total drag vs velocity for two configurations

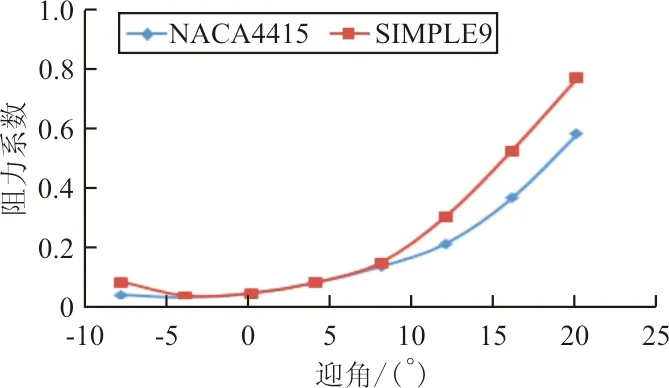
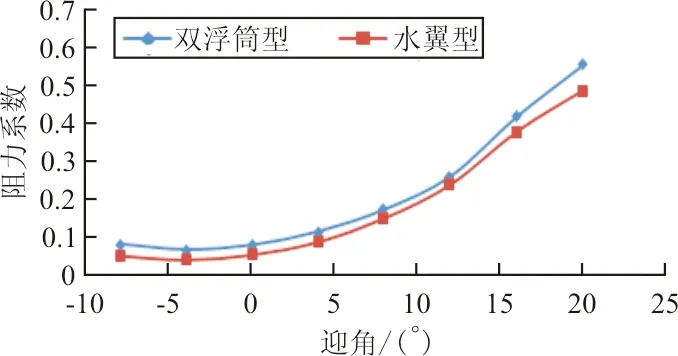
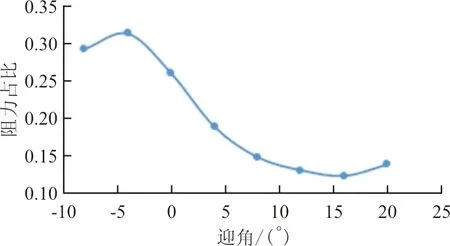
从图10可以看出：当速度V<2.5 m/s时，双浮筒型水上飞机所受阻力比水翼型水上飞机小，飞机速度较小时，水翼产生的水动升力对水翼型水上飞机浸水体积影响不大而附加的水翼增加了全机的水动阻力。速度5 m/s

以上分析说明，水翼型水上飞机偏转机翼布局总阻力总体上要小于双浮筒型水上飞机，双浮筒型水上飞机阻力峰值约为水翼型水上飞机偏转机翼布局的1.97倍，水翼型水上飞机偏转机翼布局能够有效提高水上飞机的水动性能。

3 气动特性分析

分别对水翼型水上飞机偏转机翼布局和双浮筒型水上飞机进行空中巡航气动特性计算，验证水翼型水上飞机偏转机翼布局气动特性。

3.1 气动特性计算方法验证

气动特性计算采用DLR-F6模型进行验证，CFD计算结果与文献[13]试验数据进行对比。计算状态为：雷诺数Re=5×106，马赫数Ma=0.75。选用S-A湍流模型，压力-速度耦合采用SIMPLEC算法，DLR-F6机身非结构网格如图11所示。

图11 DLR-F6模型计算网格Fig.11 Computation mesh for DLR-F6 model

DLR-F6模型数值计算结果与试验数据[13]对比图如图12所示，可以看出：CFD方法能够较准确地模拟升阻力系数变化趋势，计算误差在5%以内，说明上述计算方法适用于本文计算。

(a) 升力系数随迎角变化对比图

(b) 阻力系数随迎角变化对比图图12 DLR-F6模型CFD模拟与试验数据对比图Fig.12 Comparison of CFD simulation and test data of DLR-F6 model

3.2 水翼型水上飞机气动性能计算

为研究偏转机翼布局对飞机气动性能的影响，首先对NACA4415和SIMPLE9两种翼型的气动性能进行分析。计算模型中机翼水平状态下的水平面投影面积、根梢比及平均气动弦长相同。两种翼型飞机在巡航速度V=237 km/h下升力系数、阻力系数、升阻比随迎角变化曲线图如图13所示，可以看出：采用NACA4415翼型飞机失速迎角为12°，采用SIMPLE9翼型飞机失速迎角为8°；采用NACA4415翼型的最大升力系数约为采用SIMPLE9翼型的1.27倍，同时，迎角不超过8°时，两种翼型阻力系数缓慢增加；采用SIMPLE9翼型阻力系数与采用NACA4415翼型十分接近，当飞机迎角超过8°，采用SIMPLE9翼型飞机阻力系数急剧增加，其阻力系数明显大于采用NACA4415翼型；迎角为12°时，采用NACA4415翼型阻力系数约为采用SIMPLE9翼型的71%。采用NACA4415翼型能产生更高的升力，且所受阻力更小，同时飞机可变迎角范围更广，更适合飞机空中巡航飞行。SIMPLE9翼型为弓背形翼型，其翼面水平，翼面表面压力分布均匀，相比于NACA4415翼型，其产生局部压力极小值的概率更低，因此更不容易产生空泡，其水动性能优于NACA4415翼型。上述分析表明结合SIMPLE9翼型水动性能的优异性与NACA4415气动性能优于SIMPLE9翼型的特点，水翼型水上飞机固定机翼采用NACA4415翼型，偏转机翼采用SIMPLE9翼型比机翼采用单一NACA4415翼型或SIMPLE9翼型具有更优的水动与气动综合性能。

(a) 升力系数随迎角变化曲线图

(b) 阻力系数随迎角变化曲线图

水翼型水上飞机在空中飞行时，偏转机翼能够改变偏转角度，为分析偏转机翼偏转角度对飞机气动特性造成的影响，对飞机分别偏转后段机翼30°、20°、10°及0°四种状态进行数值模拟。后段偏转机翼不同偏转角升力占总升力比值变化曲线图如图14所示。

图14 不同偏转角偏转机翼升力占比图Fig.14 Lift proportion chart of deflecting wing at different deflection angles

从图14可以看出：不同偏转角偏转机翼升力在机翼总升力的占比变化趋势相同，偏转机翼偏转角越小，其升力占比越大。当迎角α<-4°时，后段机翼升力占比在逐渐提升，说明迎角α<-4°时SIMPLE9翼型升力增加速率高于NACA4415翼型，偏转机翼升力占机翼总升力比值最高在32%至35%之间。当迎角-4°<α<8°时，后段偏转机翼升力占比逐渐减小，此时，NACA4415翼型升力增速高于SIMPLE9翼型，升力增加主要由固定机翼提供。当迎角8°<α<12°时，后段偏转机翼升力占比减小速率加快，此时偏转机翼已超过失速迎角升力减小而固定机翼升力仍在增大，从而导致偏转机翼升力占比急剧下降。当迎角α>12°时，固定机翼已超过失速迎角，其产生升力急剧降低，偏转机翼升力占比开始上升，随着偏转机翼偏转角的逐渐减小，偏转机翼升力占比在逐渐增大，因为随着偏转角的逐渐减小，偏转机翼在升力方向的投影面积逐渐增大，升力方向力的分量逐渐增大，当偏转角为0°时，偏转机翼在升力方向的投影面积达到最大，产生的升力最大，此时整个机翼产生的升力也达到最大。

以上分析说明，水翼型水上飞机偏转机翼布局具有较好的气动特性，机翼翼型分段布置能够获得优良的水动与气动综合性能，偏转机翼偏转0°时飞机气动性能最优。

为验证水翼型水上飞机偏转机翼布局的气动性能，选用水动验证部分的双浮筒型水上飞机作为参考模型进行对比研究。使用与水翼型水上飞机相同条件对双浮筒型水上飞机进行数值模拟，得到如图15所示结果。从图15(a)～(c)可以看出：在升阻性能方面，两者升阻系数随迎角变化趋势相同。在计算迎角范围内双浮筒型水上飞机升力系数较高于水翼型水上飞机升力系数，飞机迎角8°<α<12°时，水翼型水上飞机升力系数增速慢于双浮筒型水上飞机，双浮筒型水上飞机最大升力系数是水翼型水上飞机的1.17倍，原因在于双浮筒型水上飞机机翼采用NACA4415翼型而水翼型水上飞机偏转机翼采用SIMPLE9翼型，当迎角α超过8°后，偏转机翼失速导致机翼升力上升速度变慢。在计算迎角范围内，双浮筒型水上飞机阻力系数较高于水翼型水上飞机，水翼型水上飞机最大升阻比是双浮筒型水上飞机的1.4倍，迎角α=12°时，双浮筒型水上飞机阻力系数是水翼型水上飞机的1.1倍。进一步分析尾部水翼对水翼型水上飞机阻力性能的影响如图15(d)～(e)所示，可以看出：尾部水翼阻力Dwlsy占全机阻力Dsy最高比值为0.02，而浮筒阻力Dft占全机阻力Dfj最高比值为0.31，尾部水翼阻力占全机阻力比值远远低于浮筒阻力占全机阻力比值。