不同情形下温度低于0 ℃时饱和水汽压的计算

2019-12-30

Advances in Meteorological Science and Technology 2019年6期

（吉林省人工影响天气办公室，长春 130062）

0 引言

饱和水汽压是计算空气绝对湿度、相对湿度、露点、比湿等大气湿度要素的基础。其计算公式繁多[1-4]。其中，Goff-Gratch公式是世界气象组织（WMO）1966年建议采用的饱和水汽压计算公式。针对这些公式，董双林等[5]和罗丽等[6]进行了分析，张志富等[7]进行了露点温度计算的对比分析和探讨。这些研究都是对不同的饱和水汽压经验公式的对比分析，而对于温度低于0℃时如何合理地应用相对于水面和冰面的饱和水汽压公式来计算和讨论水汽压相关问题的研究所见不多。而低温时饱和水汽压的计算至关重要，因为如果在温度低于0 ℃时就武断地应用冰面饱和水汽压公式，其计算结果和物理意义可能会存在偏差。本文利用长春站的探空资料，采用Magnus公式，通过理论分析和实例计算，讨论了在计算大气可降水量和研讨云微物理问题时，如何合理地应用相对于水面和冰面饱和水汽压公式，以期有助于对涉及大气可降水量和云降水粒子形成、增长机制相关问题的理解和研究。

1 计算大气可降水量时饱和水汽压公式的选用

1.1 大气可降水量计算方法

大气可降水量（Precipitable Water，PW），它表示单位面积垂直大气柱内所包含的水汽总量，也就是假如垂直气柱内的水汽全部凝结降落，那么在气柱底面上所聚积的液态水深度。其计算公式为：

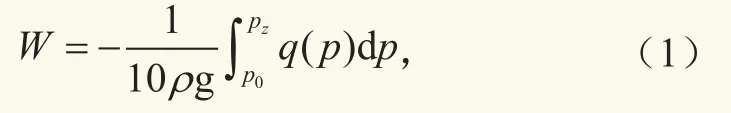
式中，W是大气可降水量，单位mm；ρ是液态水密度，单位是g·cm-3；g是重力加速度，单位m·s-2；p0、pz分别是地面和z高度处气压值，单位hPa；q是比湿，单位g·kg-1。比湿的计算公式是：

式中，e是水汽压，单位hPa；采用Magnus公式计算：

式中，A、a、b是常数，A=6.11；对于水面a=7.5，b=237.3；对于冰面a=9.5，b=265.5；td是露点温度，单位℃。因大气水汽主要集中在对流层下部，一般只需计算从地面到300 hPa处。

由上述公式可看出，水汽压是计算大气可降水量的关键。现行《常规高空气象观测业务规范》推荐使用的饱和水汽压公式是Goff-Gratch公式，其适用温度范围是-50～100 ℃，根据罗丽等[6]的研究成果，在-50～50 ℃范围内可采用Magnus公式替代Goff-Gratch公式，所以本文采用形式简洁、得到广泛应用的Magnus公式。

1.2 以-20 ℃为界的对比分析

20世纪30年代，在欧洲飞机观测发现，-20～-12 ℃的云中仍有许多过冷水滴，在-30～-20 ℃仍可观测到液滴[8]，同时，在近几年的实际业务工作中，模式计算给出的吉林省云垂直结构显示，过冷水主要集中在-20～0 ℃层。因此本文利用2018年1月和5月长春站08、20时探空资料，采用两种方法：（1）整层采用相对于水面的饱和水汽压公式计算大气可降水量Ww；（2）以-20 ℃为界，温度≥-20℃采用相对于水面的饱和水汽压公式，＜-20 ℃采用相对于冰面的饱和水汽压公式计算大气可降水量Wi。计算和对比分析1月和5月两种方法得到结果的绝对偏差Ww-Wi和相对偏差。

1月和5月两种方法得到结果的绝对偏差（图略）最大值分别为0.67 mm和0.62 mm，但1月份大气可降水量均值为3.8 mm，5月份大气可降水量均值为20 mm，可见绝对偏差不能很好地反应两种方法计算结果偏差的大小，因此重点分析两种方法得到结果的相对偏差（图1）。由图中可看出，5月两种方法计算结果的相对偏差不大，最大值出现在1日20时，也只有4%；而1月气温比较低，这时两种方法计算结果的相对偏差变化幅度较大，尤其是20日20时—27日08时，期间最大值出现在23日08时，为32%。这是由于这一期间地面温度已低于-20℃，整层大气可降水量都是由相对于冰面的饱和水汽压公式计算得到的。可见在地面温度低于-20℃时，两种方法计算结果的相对偏差较大。显然，这种相对偏差的大小与分界温度有关。

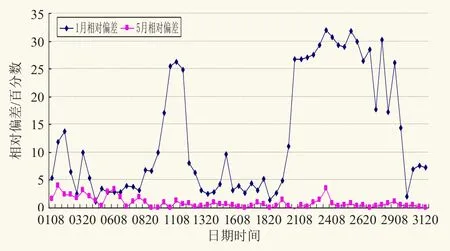
图1 以-20℃为界两种计算方法结果相对偏差Fig. 1 Relative deviation of the results of two calculation methods with -20 ℃ as the boundary

1.3 以-40 ℃为界的对比分析

一般认为纯水滴同质冻结核化温度约为-40 ℃，且有飞机实测和地基偏振激光雷达探测证实，温度在-37.3～-34.3 ℃的过冷卷云是以同质冻结核化为主[9]，说明在温度高于-40 ℃时，还是有过冷水滴存在的，本文又以-40 ℃为界，温度＞-40 ℃采用相对于水面的饱和水汽压公式，≤-40 ℃采用相对于冰面的饱和水汽压公式，计算得到了两种方法计算结果的绝对偏差和相对偏差。1月和5月两种方法得到结果的绝对偏差最大值分别为0.14 mm和0.08 mm，同样，仍是重点分析两种方法得到结果的相对偏差（图2）。这时，5月份两种方法计算结果基本一致，相对偏差最大值出现在4日08时，仅仅0.8%；且1月份两种方法计算结果的相对偏差也降低了很多，最大值出现在24日08时，为9%，其余均≤5.5%。可见随着分界温度的降低，两种方法计算结果的相对偏差也减小，计算结果也越趋于一致。如果分界温度为0 ℃，即温度低于0 ℃时，就武断地应用冰面饱和水汽压公式来计算大气可降水量，计算结果的相对偏差会更大。

图2 以-40 ℃为界两种计算方法结果相对偏差Fig. 2 Relative deviation of the results of two calculation methods with -40 ℃ as the boundary

依据现行《常规高空气象观测业务规范》，相对湿度、露点温度的计算都是基于水面饱和水汽压的，即探空所得的湿度数据在大于-60 ℃范围内（低于此温度不再计算露点温度）是相对于水面的，因此在此范围内，计算大气可降水量理应采用相对于水面的饱和水汽压公式；再者大气水汽主要集中在对流层下部，一般只计算从地面到300 hPa处，300 hPa处的温度一般＞-60 ℃，在此范围内，以-40 ℃为界，两种方法得到的大气可降水量计算结果趋于一致；所以可以整层采用相对于水面饱和水汽压公式计算大气可降水量。同时，从云物理角度来看，这一结论符合大气可降水量的定义，即“假如垂直气柱内的水汽全部凝结降落，在气柱底面上所聚积的液态水深度”，讨论水汽凝结问题理应采用相对于水面的饱和水汽压公式。如果温度低于0 ℃时，就武断地应用冰面饱和水汽压公式，物理意义会存在偏差。

2 云微物理问题中合理选用饱和水汽压公式

2.1 云滴的异质凝结核化和凝结增长

在云、降水的形成和发展过程中，大气中有些气溶胶粒子可充作凝结核或冰核。其中很大一部分为可溶性盐，如硫酸盐、硝酸盐、氯化物等，这些粒子具有吸湿性，可在不饱和条件下吸湿潮解。由于其平衡水汽压低，可先于凝结核化之前形成溶液滴，利于凝结核化形成云滴。在讨论云滴的异质凝结核化时，其周围环境和液滴表面的饱和问题，自然应用的是相对于水面的饱和水汽压公式。

在云物理学中定义饱和比s=e/es，e为实际环境水汽压，es为平液面的饱和水汽压，可以看出s亦是天气学中的相对湿度。一般认为云滴凝结增长相应大气中的饱和比为1.001～1.01，当饱和比s＞1时，水滴凝结增长[9]。考虑到有降水的天气，实际大气应存在饱和的地方。所以任一选择了长春地区有降水的一天：2018年5月29日，应用当天探空资料计算了各层的饱和比。表1列出了各规定等压面层的温度和温度露点差，表中Sw是由相对于水面饱和水汽压公式计算得到的饱和比（相对湿度），Si是实际环境水汽压e为相对于水面的，es为相对于冰面的饱和水汽压计算得到的饱和比。由表中数据可以看出，08时850 hPa和700 hPa温度露点差为1℃，这在天气学中一般认为已达到饱和（T-Td≤2 ℃），计算得到的Sw约为0.93；20时除850 hPa外，其他各层的湿度情况都要好于08时，特别是700 hPa，温度露点差为0 ℃，饱和比Sw为1，这应是探空数据能获得饱和比Sw的最大值，与云滴凝结增长相应的大气中饱和比接近。探空数据的时空分辨率远逊于机载粒子探测数据，应用机载粒子探测数据也许会得到更精准的结果。

表1 由2018年5月29日探空数据计算的饱和比Table 1 Saturation ratio calculated from sounding data on May 29, 2018

2.2 冰的异质核化

冰的异质核化方式目前理论上有4种。

1）凝结-冻结：有些核兼具凝结核和冻结核作用，其核化过程中先使水汽凝结，然后转化为浸润冻结；

2）接触冻结：其成核作用是在空气中与过冷水滴碰并，以相触的核面为冻结起点，逐渐使过冷水滴完全冻结；

3）浸润冻结：核从空气中进入过冷水滴或原先就位于过冷水滴内，以其为冻结核心，使过冷水滴产生冻结；

4）凝华：水汽直接在核上凝华成冰晶。

前3种核化方式要么是涉及水汽凝结，要么是涉及过冷水滴，可见粒子的起始生存环境都涉及液相的水，因此讨论其起始生存环境饱和问题时，考虑的应是相对于水面的饱和水汽压。第4种核化方式，凝华，相对来说要复杂些。大气中自然冰核数浓度很少，尺度也较小，观测和实验对有些核化方式不易区分。比如，即使在环境相对于水面欠饱和时核化成冰，也并不确定就是凝华，因为冰核中可含有可溶性成分，可溶性成分可在低于水面饱和时凝结核化，而其不可溶成分可冻结核化。理论上环境水汽压大于冰面饱和水汽压便可发生凝华。而一旦冰相粒子产生，其表面饱和问题就需要考虑相对于冰面的饱和水汽压。

2.3 冰、水共存

冰晶和水滴共存时，显然需要同时考虑相对于水面和相对于冰面的饱和水汽压。如果环境相对于水面是饱和的，此时实际环境水汽压就是es，由于同温度下，水面的饱和水汽压es大于冰面的ei，所以理论上冰晶表面的饱和比si=es/ei＞1，且si值随温度下降，接近于线性增加（图3），这是云中冰晶能迅速增长的有利条件。图中，在-1 ℃时，si已达到1.019；-15 ℃时，si达1.156，与水滴凝结增长饱和比（1.001～1.010）相比明显要大得多。实际大气中si又是怎样的呢？表1中，20时700 hPa饱和比Sw为1，环境相对于水面饱和，相对于冰面过饱和。此时Si值为1.039与图3中-4 ℃时的理论值一致，如果这里有冰晶存在，这里环境就是冰水共存的，且有利于冰晶增长；在400 hPa，温度-33 ℃，温度露点差为3 ℃，Sw为0.742，Si达到了1.016，可见这里环境是水面欠饱和、冰面过饱和的，且环境湿度条件较好，这里应该是有云的，400 hPa对应的高度是7 km左右，这一高度的云应是以冰相粒子为主。应该注意的是：实际大气中无论是云滴凝结增长还是冰晶吸蚀水汽增长都是动态的，对云中Sw、Si分布及降水粒子的形成、增长的研究，还需进行大量的飞机实际探测。

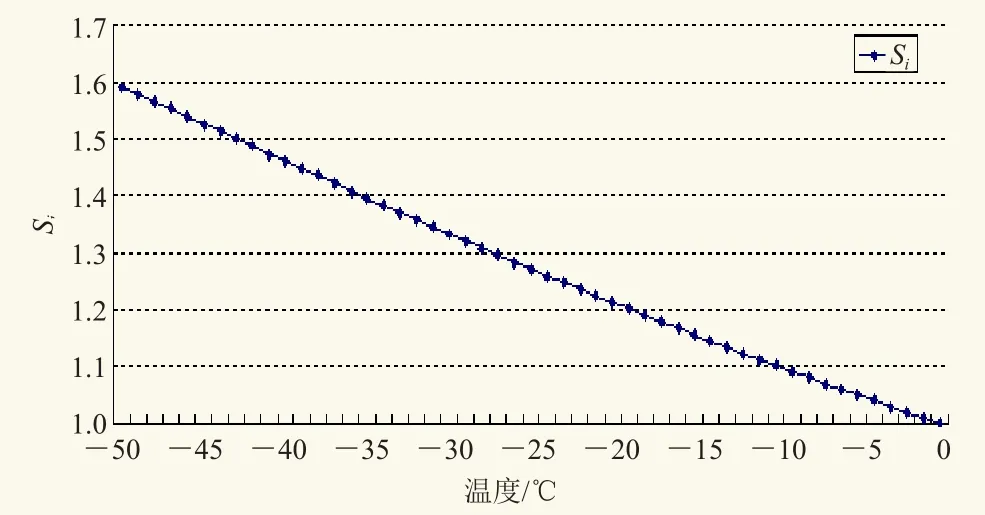
图3 环境相对于水面饱和时冰晶表面的饱和比随温度的变化Fig. 3 Variation of saturation ratio with temperature at ice crystal surface when the environment is saturated at water surface

综上，在讨论云微物理问题时，研究的是云粒子的形成、增长及产生降水的微观物理过程，这时需要根据粒子的相态和粒子所处的周围环境来考虑应用哪种饱和水汽压公式。