小学生计算思维能力调查研究——以西安市3-5 年级学生为例

王小红，赵 明

（陕西师范大学 教育学院，陕西 西安 710062）

在当前信息技术快速发展的时代背景下，处理计算机语言成为一种不可避免的技能、一种新的读写能力，能让我们充分有效地参与到信息技术中。因此，当一个人能够用计算机和其他机器语言读写，并能够用计算机的方式思考时，就被认为是懂代码的人。计算思维就是指解决问题的认知过程[1]。尽管计算思维可以转移到不直接涉及编程任务的各种类型的问题上[2]，但计算机编程是使计算思维活跃起来的基础方法。

随着信息技术的普及，计算思维越来越被视为创造而不仅仅是消费技术的基本技能[3]，许多国家对引入计算思维的兴趣重新点燃。计算思维是新一代学生需要掌握的一套解决问题的技能，长期以来被认为是学生认知发展的重要因素[4]，因此许多国家都将其纳入到国家教育课程中。英国等一些欧洲国家从小学开始引入编程教学，并将计算思维纳入到课程中。2011 年，美国计算机科学教师协会（CSTA）和计算机协会（ACM），将计算思维纳入到小学并且制定了《K-12 计算机科学标准》。2015 年，澳大利将计算思维纳入课程目标，上述均反映出各国对计算思维重要性的认识。计算思维已被描述为一项基本的技能，然而业界对其定义以及如何测量和评估尚未达成共识。

国外已有研究证明：在计算思维方面男生和女生存在显著差异，并且这种现象随着年级的增加更加突出[5]，那么在我国的基础教育阶段是否存在这种差异现象呢？因此，本文旨在提供一种新的测量计算思维能力的工具，调查在思维初步形成阶段的小学生计算思维能力现状，为后续小学生计算思维能力的培养打好基础。陈英和与赵笑梅发现：3-5 年级学生在计算机上编写程序时，已经具备类似问题解决的能力[6]，因此本次研究对象为3-5 年级的小学生。

一、研究综述

1.计算思维定义

计算思维这一术语包含着概念和思维过程，这些概念和思维过程有助于在不同的领域以一种计算机的方式形成解决方案。2006 年，周以真教授首次提出计算思维并给出正式的定义，认为“计算思维是一种利用计算机科学概念解决问题的方法，不只是计算机科学家应该具有的技能，而是所有人都应具备的技能”[7]。2011 年，其又在此基础上对计算思维定义进行了修订，认为“计算思维是一种解决问题的思维过程”[8]。随着计算思维的不断深入，学者们纷纷对计算思维进行定义。2011 年，美国国际教育技术协会（ISTE）和计算机科学教师协会（CSTA）联合认为“计算思维是通过数据收集、数据分析、数据表示、问题分解、抽象、算法和程序、自动化、模拟和并行化等环节进行问题解决的过程。”[9]这也是计算思维最常见的两种定义，但目前并没有形成统一。

通过对已有文献的梳理发现，计算思维定义使用最多的词汇有：问题解决、抽象、过程、数据、概念、算法、求解、自动化等[10]。并将计算思维归纳为问题解决说、系统说、过程说、活动及方法说、工具说等[11]。

2.计算思维评价

目前关于计算思维的评价并没有统一的工具，然而验证过的测量仪器在任何研究领域都是有价值的。近年来，我们发现对中小学的计算思维进行测量和评估的尝试是值得关注的。

Werner 等人在研究中使用了一个基于Alice 平台的“仙女评价”系统，试图调查学生在问题解决过程中对计算思维概念的理解和使用情况[12]。然而，该仪器只针对Alice 编程学习环境，并没有经过心理测量学验证。美国克莱姆森大学的研究小组提供了一个互补的观点。这些学者提出了一个动觉的学习方法（具体学习）来评估五年级和六年级学生的计算思维。为此，他们在Alice 环境中运行序列编程（舞蹈）活动，在物理动觉环境中表示相同的序列。评估工具也结合了这两种设置，但其心理测量特性尚未报告。

另外，美国科罗拉多大学的小组也提供了一个有趣的研究方向，他们与第一组视频游戏编程环境中的学生合作，在年轻程序员创建视频游戏的背景下，设计了计算思维模式图，用于分析学生编程的游戏，并以图形化方式与模型相比，每个游戏涉及不同计算思维模式的程度[13]。第二组研究试图评估学生是否能够将视频游戏编程期间获得的计算思维模式转移到科学模拟编程的新环境中[14]。针对这一评估，他们开发了计算思维模型的测试工具，其可靠性或有效性尚未报告。

同样，来自西班牙马德里大学的学者介绍了一种Dr.Scratch 开源的Web 应用程序，旨在简单、自动地分析Scratch 编程项目[3]，并提供反馈，可用于提高编程技能和发展学生的计算思维。为了给项目一个整体的计算思维评分，Dr.Scratch 从七个维度推断程序员的计算思维能力，即问题的抽象、分解、并行、逻辑思维、同步、流程控制、用户交互和数据表示。其并非严格意义上的认知测试，而是Scratch 程序的形成性评价工具。该程序目前正处于验证过程中。

此外，2003 年在立陶宛诞生了Bebras（国际计算思维挑战赛），目的是通过计算思维挑战增强小学生对计算机科学领域的兴趣[15]。其每年比赛都会提出一套Bebras 任务，通过计算思维的转移和投射来解决所面临的问题，这些问题独立于任何软件或硬件，可以提供给任何没有编程经验的人。但是目前Bebras 国际比赛只是作为一种推广计算思维的活动，并不是一个测量工具。

Buffum 等人开发了一套测量5-10 年级学生计算思维发展水平的计算思维能力测试量表，测试总共包括28 项题目，依靠计算概念和使用编程语言的逻辑语法来制定解决问题的能力[16]。目前只有Román-González 等结合标准化心理测试对计算思维能力测试量表进行了验证，并分析了计算思维能力测试量表的效度[5]。

因此，本次调查将计算思维能力测试量表进行了翻译，并对小学3-5 年级的学生进行了测试，发现3、4年级的学生是可以完成这份量表的。

3.计算思维性别差异

国外有研究证明学生计算思维能力发展方面存在性别差异。Espino &González 在FLL 机器人竞赛调查中发现性别分化明显，男生的人数多于女生[17]。此结果可能是由于性别的刻板印象而形成的。Román-González等人在西班牙进行计算思维测验时，发现计算思维在性别方面存在显著的差异，而且会随着年级的增长差距越来越大[5]。而Werner 等人在调查学生两年来计算思维发展与性别的关系时，发现计算思维与性别之间没有显著差异[12]，可能是在本次调查中女生仅占36%，男女人数比列差距相对较大的原因。

关于性别差异方面的研究，国外大多数学者认为存在显著差异，也有一部分人认为没有差异，但是我国关于这方面的调查相对较少。

二、研究工具

本研究根据Buffum 等人开发的计算思维能力测试（CTT）量表，旨在测量学生的计算思维能力发展水平[16]，包含计算思维的基本概念和使用编程语言的逻辑语法来制定和解决问题的能力。计算思维的基本概念即序列、循环、迭代、条件、函数和变量。这些概念与计算思维三维框架中强调的计算思维概念相一致[18]。计算思维能力测试量表共28 道单选题，每项包括一个或多个计算概念，其中基本序列（4 项）、循环（8 项）、条件（12 项）、函数（4 项）；界面主要以迷宫（23 项）和画布（5 项）的形式呈现；选项主要以箭头（20 项）和积木（8 项）呈现问题解决方式（如图1 所示）。题目中包含计算思维概念和计算思维的实践，这与计算思维三维框架一致。

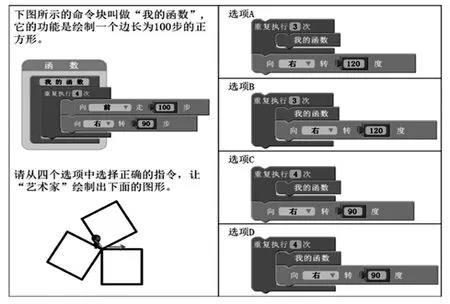
图1 计算思维能力测试量表题项

三、研究对象与实施

1.研究对象

本研究按照地理位置采用分层多阶段整体随机抽样方法，把整个西安市13 个区县划分为中心城区、郊区和远郊区三个区域。从每个区域抽取两个区县，每个区县再从小学3-5 年级中随机抽取一个班级参与测评。

2.问卷的发放与回收

问卷是以问卷星的方式进行发放，通过QQ 群将问卷链接转发给各个区县的信息技术教师，教师在信息技术课程上督促学生完成或学生在家自主完成问卷，总共回收550 份，其中有效问卷为542 份，有效率达98.5%，不同地区、不同年级的学生样本如表1 所示。

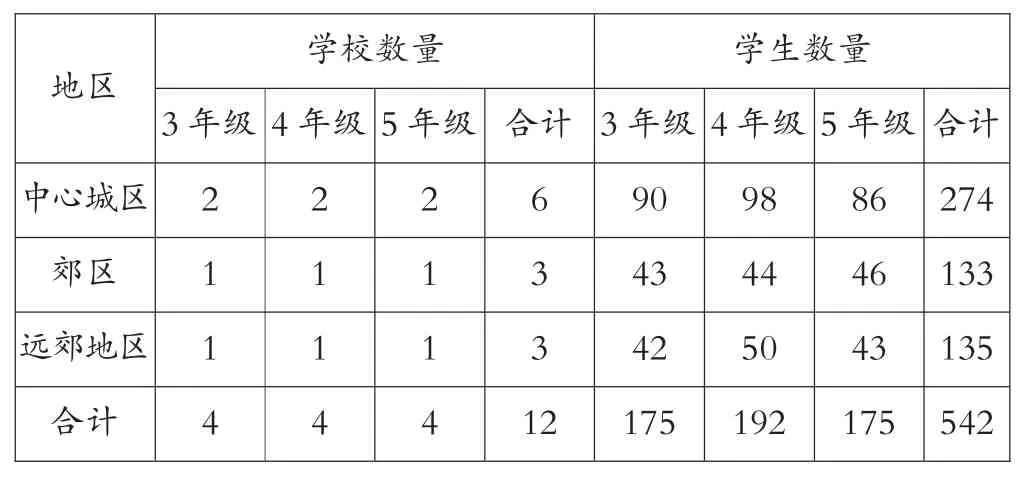
表1 不同地区、不同年级抽样学校数和学生数量

四、结果分析与讨论

1.描述性统计分析

对所收集到的有效数据整理分析，如表2 所示为整个样本的计算思维能力测试得分的描述性统计分析，按照28 个题目正确得分之和计算而得（n=542），其中平均分数为13.81，最高分数为27 分，最低分数为4 分。

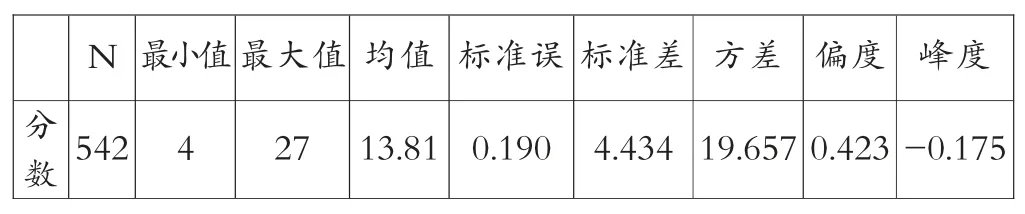
表2 计算思维测试分数描述性统计分析

计算思维能力测试评分的分布直方图如图2 所示，评分分布与正态分布曲线吻合。考虑到样本的容量比较大，分数的双侧显著性值为sig=0.000，小于0.05，故拒绝了正态性的原假设。

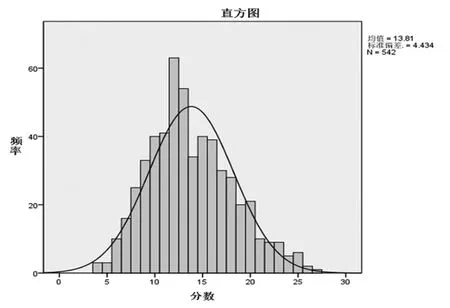
图2 计算思维测试评分的直方图

28 项题目的成功率或项目难度指数如图3 所示，证实了计算思维能力测试量表渐进的难度，在内容方面专家们已经预料到了这点。28 道题目的平均成功率为0.49（中等难度），范围从0.13（第23 道题具有非常高的难度）到0.95（第1 道题难度非常低）。

图3 计算思维测试难度指数

综上所述可知：计算思维能力测试评分呈正态分布，显示出适当的变异性，因此可以为目标人群构建适合的尺度；对目标人群而言，计算思维能力测试量表具有适当的难度（中等），而且整个题目的难度越来越大。

2.不同年级分析

按照测试者的不同年级将样本进行分割，得到表3所示的描述性统计分析。由于六年级学生面临升学压力，本次测试的调查对象为小学高年级中的3-5 年级。

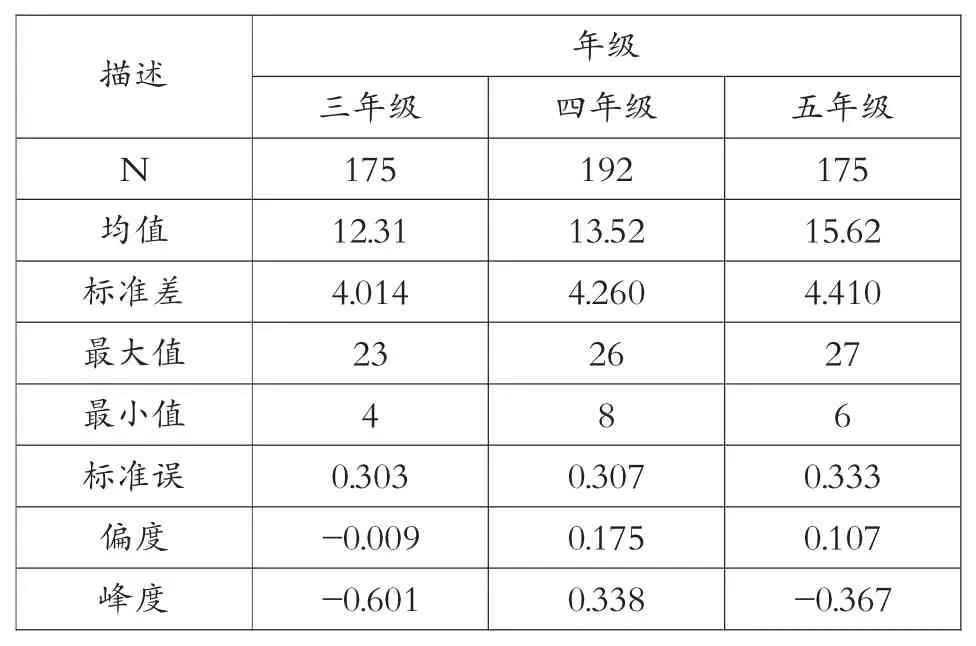
表3 不同年级计算思维测试评分描述统计分析

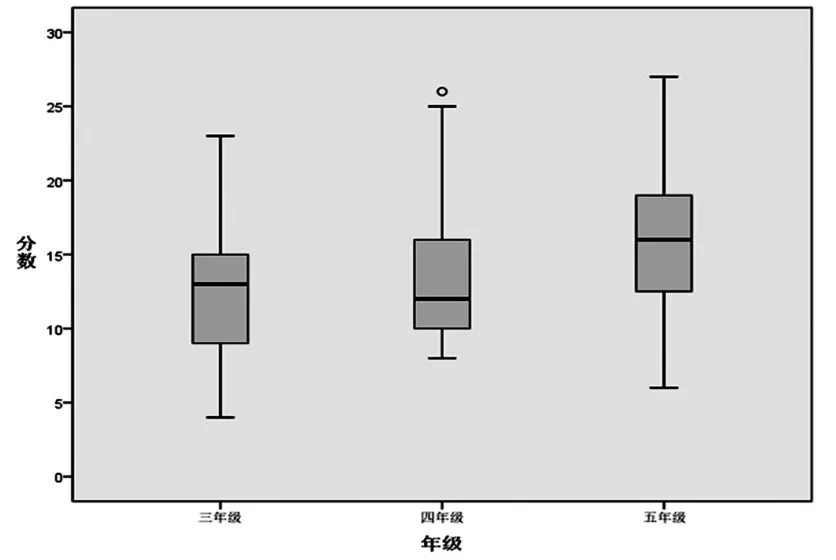
图4 计算思维测试难度指数

不同年级学生计算思维能力测试得分如图4 所示，四年级出现了离散值情况，在计算思维能力测试中获得了26 分的评分。单因素方差分析显示计算思维能力测试得分与年级在统计学上有显著差异（F=27.419，p＜0.01），说明计算思维能力测试得分随着年级的增加而增加，这个结果与我们的假设一致，即计算思维是一种解决问题的能力，与受试者的认知发展联系起来[19]。

3.不同性别分析

如表4 所示，在计算思维能力测试评分中男女生的得分在统计学上有极其显著的差异（P=0.000,p＜0.01）。效应量测量Cohen's d 为0.51，被认为是一种中度效应。按照年级来分析性别差异，计算思维能力测试评分中男生的均值始终高于女生，性别差异在四年级（t=2.507，p＜0.05）和五年级（t=4.452，p＜0.01）有统计学意义。

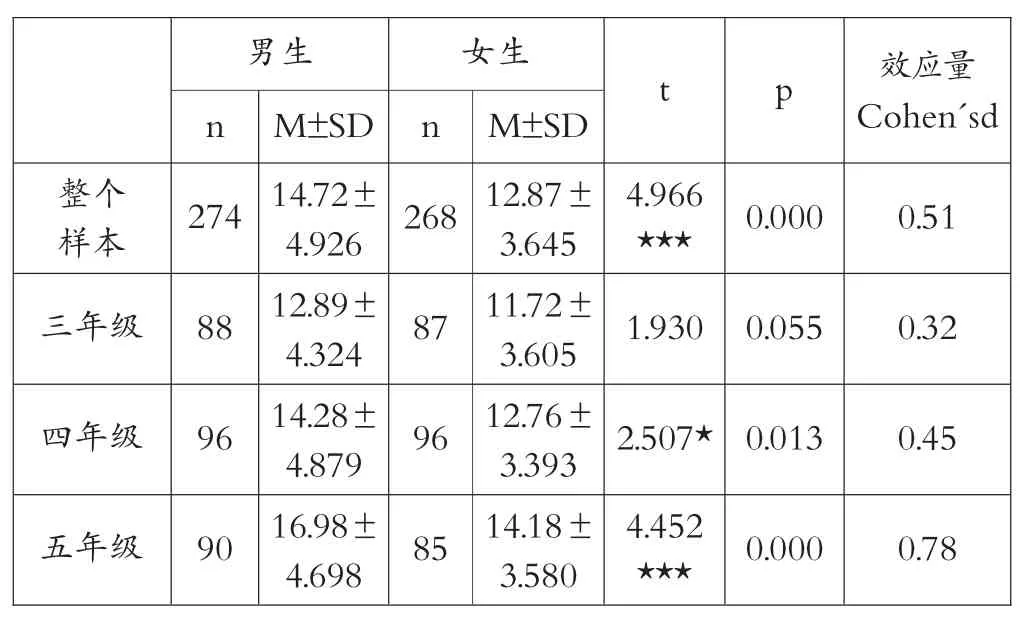
表4 计算思维能力测试对立样本T 检验

可见计算思维能力的性别差异是一个渐进的差异，随着年级的升高而增加(如图5 所示)。这与之前Bebras 的调查研究中的性别差异结果一致[20]。

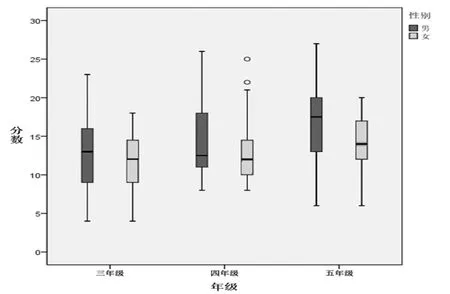
图5 计算思维测试性别差异

4.信效度检验

计算思维能力测试量表的内部一致性信度Alpha的值为0.737（见表5），表明信度良好。对不同年级学生评分的可靠性进行研究时，发现四年级学生的回答准确性更低，三年级的准确性是最高的，这与年级越高准确性越高的结果呈相反趋势。

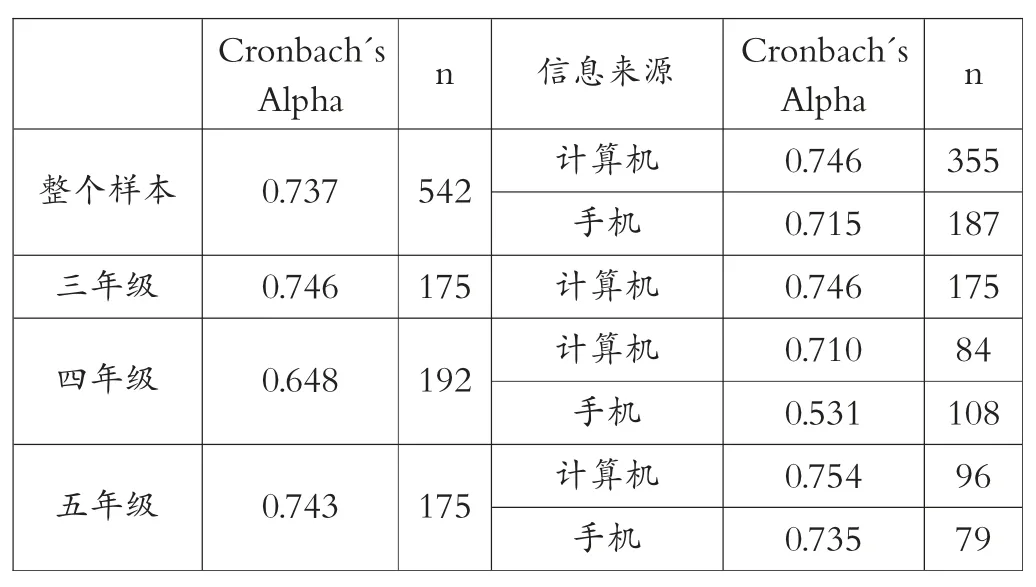
表5 计算思维能力测试内部一致性

但是对计算思维能力测试数据来源进行分析发现，来源于计算机的数据正确性更高，这可能与在教师的监督下学生更认真、更集中精力完成测试有关，避免了学生随意填写的可能性。这一解释得到了在计算机上进行计算思维能力测试和在手机上进行计算思维能力测试得分结果的支持，使用计算机的平均得分为13.90，使用手机的平均得分为13.63。

5.计算思维概念维度分析

计算思维能力测试量表中计算思维概念包括五个维度，即顺序、循环、条件、并行和函数，数据分析如表6所示，从中可以看出学生在计算思维概念方面，顺序概念是相对较好掌握的，而并行和条件是相对较难掌握的。而且随着年级的增高，所有计算思维概念的维度都会有所提升。所有的计算思维概念维度中都是男生平均得分高于女生平均得分，但是性别差异仅在三年级函数概念方面存在显著差异，男生分数明显高于女生分数（p=0.014＜0.05）,五年级学生在并行概念方面存在显著的性别差异，男生分数明显高于女生分数（p=0.012＜0.05）。

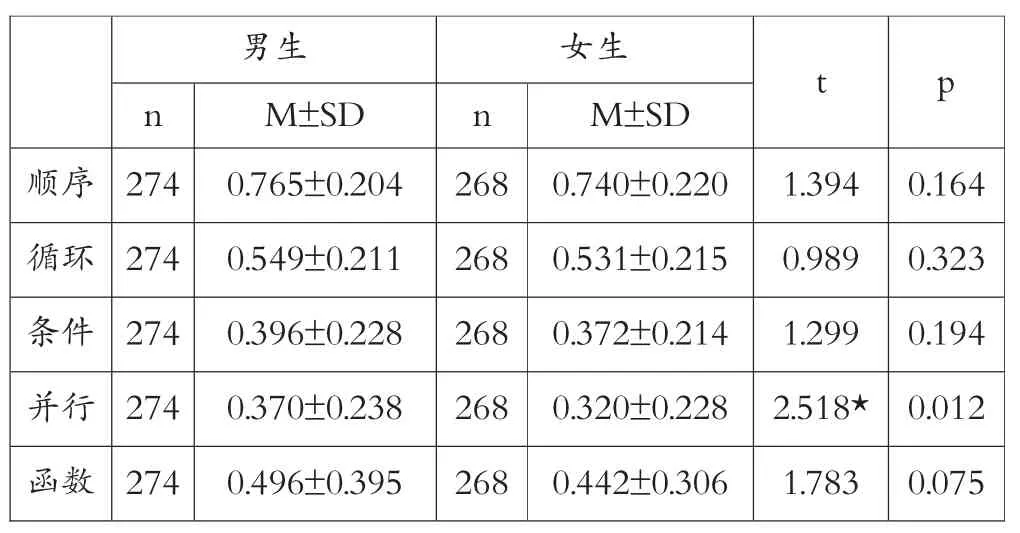
表6 计算概念各维度对立样本T 检验

6.影响和限制

计算思维能力测试量表有一些优势，开发者预定的测验对象为5-10 年级，但在试测中发现可以应用于3、4 年级的学生，这个阶段的学生思维能力已经形成，因此可以衡量没有编程经验的3-10 年级学生的计算思维水平。计算思维能力测试可以用来收集量化数据，也可以用于筛选和早期发现对编程任务解决能力较高的学生，并可以在培养学生计算思维的课程和项目前后进行评估，而在已有的文献中将其应用于收集定性数据。

然而计算思维能力测试量表也有它的局限性，主要表现为以下几个方面：①计算思维能力测试量表提供静态和非文本化的总结性评估。因此需要与其他形成性迭代测评工具结合使用，如针对不同编程环境的评价标准，支持Scratch 编程环境的Dr.Scratch 的评估、Ninja Code Village 和Grover 等人开发的针对Blockly 的工具[21],以及适用于Agent Sheets 的计算思维模式CTP 图形[13]。②计算思维能力测试量表过于关注计算思维框架中的计算概念，仅有一部分涵盖计算实践，而忽略了计算观念维度，因此应该与建立调查学生计算思维能力（CTS）态度的量表[22]相结合。③由于计算思维能力测试量表的设计是选择题，因此可以在较低的认知复杂程度下测量计算思维。采用多种手段并用的方法，结合CTT、Bebras 和Dr.Scratch 以及访谈等测评工具，用开放的复杂问题唤起项目的正确算法，以及在解决方案中让学生将计算思维转移到不同的领域，测量更高复杂程度的计算思维。

五、结论

本文提供了一种新的计算思维评估工具，通过计算思维能力测试量表对西安市小学3-5 年级542 名学生的计算思维能力发展情况进行了调查，并分析了小学阶段学生计算思维能力的性别差异。研究结果显示，3 年级的学生已经具备基本的计算思维能力，并且随着年级的增长计算思维能力有所提升，同时男女之间计算思维能力的差异越来越显著，整体上男生的计算思维能力要高于女生。因此，笔者建议要在这种现象形成初期，对学生进行干预以避免该现象的持续加深，并在教学干预中应该注重相关知识的传授。