用直线运动的公式直接解平抛运动算错吗

周久波

(连南民族高级中学 广东 清远 513300)

【例1】一物体在0.8 m高处以3 m/s水平抛出，求落地时速度大小(g取10 m/s2)．

分析：部分学生解答如下.

由

代入数据得

vt=5 m/s

而一般解法应该是：

竖直方向由

得

vy=4 m/s

再由

代入数据得

v=5 m/s

在匀变速直线运动中，学生已经熟练掌握了匀变速直线运动的公式，常用的有5个，分别是

Δs=aT2

我们知道，它们不仅适用于匀减速、匀加速，还适用于先匀减速后匀加速的往返情况(如,竖直上抛运动等)，它们都是矢量式，对于直线运动的情况，在规定正方向后，矢量运算就可以转化为代数运算．其实，这些公式在注意其矢量性后，在匀变速曲线中也可以大显身手，本文重点分析前3个公式(另外两个可由读者自己证明)．

1 证明vt=v0+at可以用于匀变速曲线运动

如图1所示，一小球以v0斜向上抛出，v0与水平方向夹角为θ，求t时间后小球速度．

图1 斜抛小球情形

解：因为加速度为g，则

vt=v0+at

变为

vt=v0+gt

如图2所示，做出v0及gt的矢量图，并首尾相连，图中vt则为t时间后小球速度．

图2 几个物理量的矢量图

根据余弦定理，速度大小可以表示为

又由于

则

速度方向与水平方向夹角

(当φ为正，表示速度斜向上，当φ为负，表示速度斜向下．)

我们再用一般的解法来解，然后对比结果．

解：如图3所示，v0可以分解为水平方向的v0cosθ和竖直方向的v0sinθ．

规定竖直向上为正方向，则

vy=v0sinθ-gt

图3 速度的分解

又由于

vx=v0cosθ

则t时间后小球速度大小为

将完全平方公式展开，很容易证明出和上面的结果是一样的．

同样，速度方向与水平方向夹角表达式也与上面结果一样．

可以看出

vt=v0+at

可以用于匀变速曲线运动(但一定注意其矢量性)，在上面的例子中，公式

vt=v0+gt

也体现了抛体运动是由匀速直线和自由落体两个运动合成的．

2 证明可以用于匀变速曲线运动

如图4所示，一小球以v0斜向上抛出，v0与水平方向夹角为θ，求t时间内小球位移．

图4 斜抛小球情形

解：因为加速度为g，则

变为

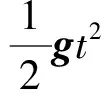
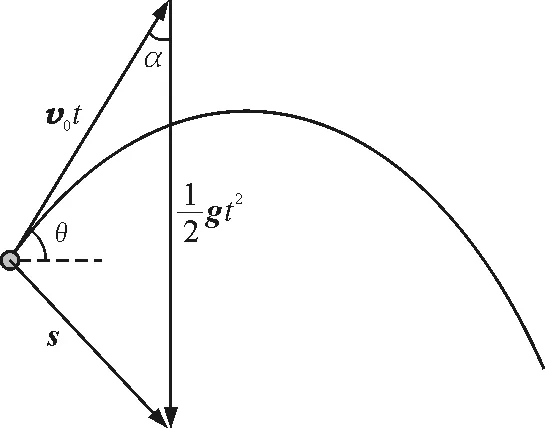
图5 几个物理量的矢量图

根据余弦定理，位移大小可以表示为

又由于

则

位移方向与水平方向夹角

(当φ为正，表示位移斜向上，当φ为负，表示位移斜向下．)

同样，用一般的解法来解(此处不再解)，然后对比结果也是一样的．所以

可以用于匀变速曲线运动(但一定注意其矢量性)，在上面的例子中，公式

也再次体现了抛体运动是由匀速直线和自由落体两个运动合成的．

3 证明可以用于匀变速曲线运动

因为加速度为g，则

变为

根据向量的性质，上式变为

vt2-v02=2gscosα

(α为重力加速度与位移的夹角)

又由于

h=scosα(对于斜向上抛，h可以为正，也可以为负)

所以大小上满足

其与动能定理

4 结束语