剖析知识建立过程挖掘核心素养教育元素——从高中物理功的教学说起

唐黎明

(上海市宝山区教育学院 上海 201900)

《普中高中物理课程标准》[1]指出能量观念是物理核心素养 “物理观念”方面中的三大要素之一，可见其在高中物理教学中的地位，物理同仁都知道学习能量是离不开学习功的，学习能量在很大程度上是在学习功和能的关系，而通常来说总是先学功，再学能，所以学习功是学生建立能量观念的首要一步；长期的中学教学经验又告诉我们，学习抽象的功的概念大部分学生是有困难的，鉴于上述2个原因，本人觉得探讨功的教学问题具有一定的现实意义．

1 教材中的思维路径

无论是现行的人教版高中《物理·必修2》[2]，还是上科版物理高一年级第二学期[3]，关于功的定义式W=Fscosθ都是通过下面的思维路径寻得的．

(1)回忆初中物理功的定义式W=Fs，并指出该定义式只适合图1所示的力F和位移s同方向的时候，并说明当F和s垂直时F不做功．

图1 力F和位移s同方向

(2)分解力F．首先提问，当F和s如图2所示成θ角时如何来计算力F的功？根据的力等效替代思想，可以将力F沿平行于位移s方向和垂直于位移s方向分解，得到Fx和Fy，如图3所示.

图2 力F和位移s同成θ角

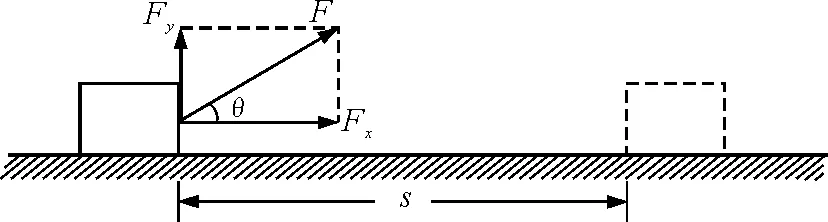
图3 对力F进行分解

(3)推出W=Fscosθ．由于Fy和s垂直，所以Fy不做功，即做功为零；又Fx=Fcosθ，W=Fxs，所以有W=Fscosθ．

(4)讨论正功、零功和负功．

1)当0≤θ<90°时，cosθ>0，所以W>0，F做正功；

2)当θ=90°时，cosθ=0，所以W=0，F不做功；

3)当时90°<θ≤180°，cosθ<0，所以W<0，F做负功．

由此，得到了功的一般定义式W=Fscosθ．

2 被强加的逻辑前题

表面上看来，教材通过上面4步“逻辑”地推导出了W=Fscosθ，如果课堂教学只是就事论事地按这4步来教授，那么不仅教师在逻辑上感到“生硬”，而且学生在知识内化上也会感到W=Fscosθ是被莫名强加的．

上面4步中除了第(1)步，只是复习学生在初中已具备的知识外，后面3步分别潜在地采用了学生所不具备的、可用于计算功的知识，来作为推理的前题．

第(2)步中所采用的推理前题是：力的合成与分解知识可用于功的计算．熟悉高中物理教学的老师都知道在还没有学习功以前，力的合成与分解知识只在静力学和动力学范围内被运用，教材不加说明地直接将其用于计算功，悄悄地将这一知识的运用范围扩大了，实为唐突．

第(3)步中所采用的推理前题是：合力做的功等于各个分力所做功的代数和．这一知识应该是在学生掌握W=Fscosθ之后，再来学习的，但教材显然是先“盗用”了，有“逻辑循环”之嫌．

第(4)步中所采用的推理前题是：图2情景(0<θ<90°)下推出的W=Fscosθ，也适用于90°<θ≤180°下的物理情景，也就是说教材不加说明地将在一定情景下推出的物理公式扩大了适用范围，这与第(2)步中扩大知识的使用范围类同．

通过上面分析，我们不难明白对于“功”按教材直接进行教学，从认知角度上来看难以接受的原因了．

3 必要的知识引导

为了避免这种逻辑上的“生硬”，我们不妨大大方方地将这些学生还不知道的、推理的前提性知识先明确地告诉学生， 为学生将要进行的推理做好知识铺垫．实际上这些知识是学生进一步学习新知识所必需的“内部条件”[4]，当学生还不具备这些“内部条件”时按上述路径来教授“功”自然是不成功的．在教学思路上可以补充下面的引导，以帮助学生建立这些“内部条件”．

对于第(2)步，首先需要向学生说明的是：将力F分解为Fx和Fy，即用Fx和Fy来替代F，Fx和Fy将不会改变物体的运动情况，所以计算F做的功可以转化为计算Fx和Fy做的功．那么沿哪二个方向分解F才使得初中学的功的知识有用呢？按图3所示来分解F学生是容易找到的．

对于第(3)步，首先需要向学生说明的是F做的功等于Fx，Fy分别做的功的代数和，而不是矢量和，顺便指出功是标量

对于第(4)步，首先需要向学生提出问题：如图4所示，若F方向和位移s方向成钝角，则又如何来计算F的功呢？公式W=Fscosθ中θ角的取值范围是否可以拓展至钝角甚至180°呢？其次告诉学生在物理学中规定θ角的取值范围正是[0，180°][一道可以作为课后的作业：试问θ角的取值范围有必要增加(180°，360°]范围吗？]，再次才来讨论功的正、负问题．

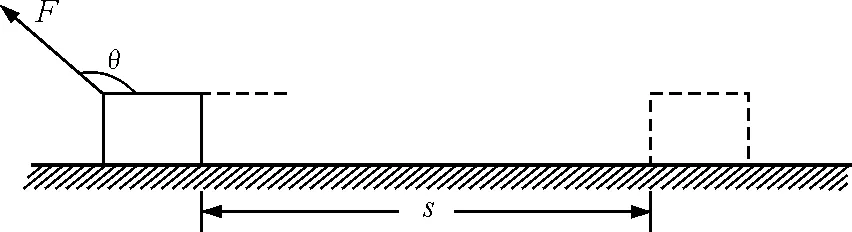
图4 力F与位移夹角θ为钝角

最后，有必要对学生作进一步的阐明，对于功的定义式W=Fscosθ与其说是推导出来的，不如说是依据合理的假设前提建构出来的，W=Fscosθ不仅包含已学的特殊形式W=Fs，而且扩展了计算功的适用范围，对于学生来说开阔了计算功的视野，寻得了在更大范围内对功的认识，所以由W=Fs到W=Fscosθ学习，属于奥苏伯尔有意义言语学习理论中的“上位学习”[5]，学生在脑中建立了关于功的较一般的知识(功的最一般的定义式在大学物理中学习)．

4 建构法

联想到当前物理核心素养中的科学思想方面，发现上述W=Fscosθ的建构过程，具有培养学生创新思想的价值，这种创新不同于通过归纳法去实现，也不同于运用类比法去发现，而是通过将已学的知识运用于更一般的情景，并采用合理的假设，从而产生包容性更广的知识来实现，我们把这种创造新知识的方法叫做建构法，建构法实际上综合地运用了假设、演绎和类比等思想方法，这是一种综合的思想方法．举例来说，量子力学中德布罗意的物质波假设的提出，就运用了建构法，因为他把光的波粒二象性，推扩到了所有实物粒子身上，在思想方法上不仅有类比，更采用了一般的假设．当然，运用建构法得出的结论在理论上或许是合理的，但也有可能面临着没有实际物理意义的风险．尽管如此，众所周知物理学中的许多创新成果正是在合理外推，大担假设的情况下取得的．

为了能够更好地在一线课堂全面落实物理核心素养教育，我们要全面地分析教材，解读教材，通过对物理知识建立过程的剖析，深刻挖掘教材中物理核心素养教育的元素，将这些潜在的“元素”显性化，不愁素养教育不能“落地生根”，上述关于功的教学问题的阐述，就作为挖掘教材中物理核心素养教育元素的一个例子，供大家参考．