刚体力学积分习题中体元选取方法*

丁学成 冯晓敏

(河北大学物理科学与技术学院 河北 保定 071002)

1 引言

力学课程是物理学及相关专业学生的基础课，也是学生步入大学后的第一门物理课程，部分学生学习起来比较困难，特别是刚体力学部分，中学与大学学习方法不同以及数学基础较弱是困扰学生的两个主要因素. 通过多年讲授力学课程发现数学基础薄弱这一因素更为关键，学生本来对定积分就比较陌生，到学习计算刚体的质心位置、转动惯量和摩擦力矩时，所给定义式为三重或二重积分的形式，考虑到学生没有学习多重积分，而在例题和习题中只计算一些简单的定积分，即通过合理选取体元或面元将三重或二重积分简化成定积分[1～3]. 但对在何种条件下，如何选取体元或面元才能将三重积分或二重积分的定义式简化成定积分来计算没有详细的解题过程，致使学生理解不到位，只能采用“模仿式”的方法做题，遇到没见过相类似的例题时就束手无策了. 另外，在定积分的计算过程中，有时用直角坐标，有时用柱坐标系或极坐标系，学生对如何选取合适的坐标系进行积分也感到困难.

本文从物理概念出发，结合截面积分法和二次积分法，并考虑到不同坐标系下体元或面元的具体表示形式，实现了三重或二重积分的定义到定积分计算的衔接.

2 计算刚体质心位置过程中体元的选取方法

刚体质心位置rc的定义式为

(1)

其中dV为质元的体积，ρ为刚体dV处的密度，r是质元dV的位置矢量. 在直角坐标系中，质心位置坐标记作xc,yc和zc，dV写成dxdydz[4]，则有

(2)

就数学而言，式(2)是3个三重积分，三重积分计算常用的方法有三次积分法、投影法(“先一后二”法)和截面法(“先二后一”法)，其中截面法是一种计算三重积分的最简单、最快速的方法[5]，将此方法应用到刚体质心位置和转动惯量的计算中，使积分过程变得非常简单.

先来介绍一下截面法，设空间闭区域

V=(x,y,z)|c≤z≤d,(x,y)∈Dz

则有

(3)

如果在被积区域内被积函数仅是z的函数，则

(4)

其中σ(z)为截面的面积，记作面元，把σ(z)dz记作体元.

力学中计算质心时，一般只需要计算一个分量，另外两个分量可以根据对称性求出[1]，并且密度ρ多为常数或仅随需要积分这个坐标变化，例如需要通过积分得到xc，则密度ρ仅是x的函数，即ρ=ρ(x). 以需要计算xc为例，则式(2)中分子的被积函数可以写成fx=xρ(x)仅是x的函数，分母被积函数ρ也只是x的函数，则有

(5)

面元σ(x)是垂直于坐标轴x的平面，或者说σ(x)内各点的x值相等，x是体元σ(x)dx的位置，这与质心位置定义式中坐标x是体元dV的坐标相一致.

则

图1 圆锥体体元示意图

由式(5)得

(6)

根据对称性可以得到

yc=zc=0

如果密度ρ为常数，则式(5)可以简写成

(7)

3 计算刚体转动惯量过程中体元的选取方法

刚体转动惯量的体元选取方法和质心位置计算相似，但是刚体定轴转动和无滑滚动都需要圆柱体对柱体轴线的转动惯量.由于圆柱体的积分侧面为柱面，一般用柱坐标积分比较方便.刚体转动惯量I的定义式为

I=∭Vr2ρdV

其中r为轴到dV的距离，ρ为dV处的密度，在柱坐标系下dV=rdθdrdz. 如果密度ρ仅是r的函数，可以看出，在转动惯量定义式中被积函数fθ,r,z=r2ρ(r)仅是r的函数，则可以采用截面法进行积分，这时转动惯量的定义式可以写成

(8)

其中R为圆柱体半径，σ(r)为截面的面积，记作面元，把σ(r)dr记作体元.

例如求半径为R，高为h，密度ρ=ρr(r≤R)的圆柱体对柱体轴线的转动惯量. 在距轴线为r处，取一厚度为dr,高为h的薄圆筒作为体元，如图2所示. 可以看出，σr=2πrh,则

(9)

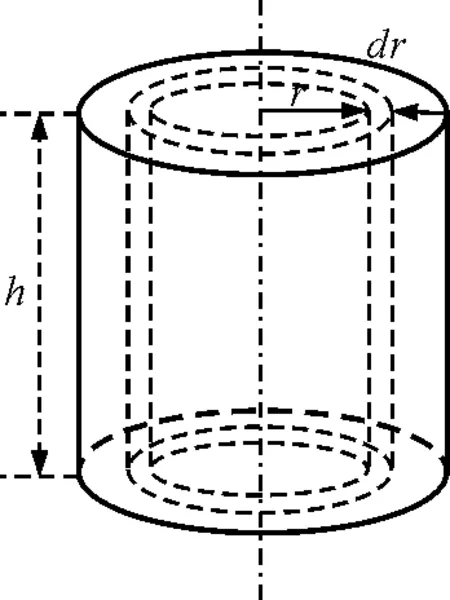
图2 圆柱体体元示意图

若密度ρ为常数，则

其中m=ρπR2h为圆柱体的质量.

4 计算摩擦力矩过程中面元的选取方法

质点所受力矩M的定义式为M=r×F，其中r为从轴或点(参考点)到力的作用点的矢量，F为质点受到的合外力. 假设力均匀分布在一个平面内，任一面元所受摩擦力为df，r为从轴或点指向df的作用点的矢量，设受力区域(积分区域)为S，则整个平面受到力矩M可以写成

M=∬Sr×df

(10)

要想把式(10)的积分结果计算出来，首先将矢量积分变成标量积分，这就要求所有矢量元(r×df)的方向相同或对其进行分解，典型习题为摩擦力矩的计算.

例如将一半径为R，面密度为σ的薄圆盘放在摩擦系数为μ的水平桌面上，求其绕垂直于桌面的中心轴O转动时的摩擦力矩. 整个圆盘各点均受到摩擦力，若圆盘按如图3所示方向转动，盘上各点的摩擦力矩均垂直于图面指向外，并且r⊥df，df可以写成df=μgσdS，因此可以将式(10)矢量积分转化为标量积分，有

M=∬Srdf=∬SrμgσdS

(11)

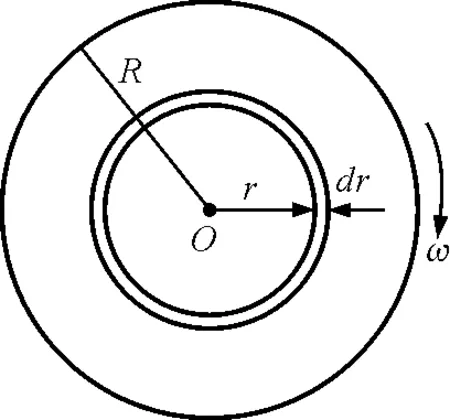
图3 圆盘面元示意图

本题的积分区域为圆域，一般采用极坐标比较方便，在极坐标情况下，面元dS=rdθdr，并且被积函数fθ,r=fr，仅是r的函数，二重积分可以变成二次积分

(12)

针对本例题，fr=rμgσ，Ar=2πr，代入到式(11)得

其中m为圆盘的质量. 如果面密度σ和摩擦因数μ是r(r≤R)的函数，式(12)仍然适用.

5 结束语

利用三重积分的截面法和二重积分的二次积分法，实现了用三重或二重积分定义的定义式到定积分计算的衔接. 并注意到积分区域的侧面为柱面时，使用柱坐标比较方便；而积分区域为圆域时，使用极坐标比较方便. 并通过例题详细讨论了用三重或二重积分定义的定义式到定积分计算的取元和解题过程.