连续型贝叶斯网络在制丝工艺过程稳态优化中的应用
2019-12-28文里梁陈爱明何邦华温亚东曾仲大
周 冰,唐 军*,文里梁,侯 岩,陈爱明,何邦华,温亚东,曾仲大
1. 云南中烟工业有限责任公司,昆明市五华区红锦路181 号 650231
2. 大连达硕信息技术有限公司,辽宁省大连市高新园区礼贤街32 号 116023
制丝工艺参数对于烟丝耐加工性、填充值以及苯酚、羟基化合物等指标均有显著影响[1-3],制丝工艺过程的稳定有助于保证卷烟产品质量[4]。但由于受设备状态、来料质量、生产环境等因素的影响[5],在生产过程中需要进行制丝工艺过程稳态优化,通常分为制丝设备优化和工艺参数优化两大类。其中,制丝设备优化主要通过维护或调整设备状态,实现工艺参数稳定。例如,陈勇等[6]通过优化烘丝机排冷凝水管路,提高了筒壁温度SD 值合格率;普绍清等[7]采用管塔相结合的干燥方式优化烘丝过程。工艺参数优化主要采用数据分析等方法考察可调参数对关键参数的影响,制定调节策略,保证关键参数的稳定性。例如,董高峰等[8]采用BP 神经网络模型研究了烟梗最佳工艺参数组合方案,提高了梗丝质量及其适配性;刘炳军等[9]采用回归分析法研究了烘丝工序工艺参数间相关性,提高了批次间稳定性;陆琨等[10]采用多元线性回归算法等技术分析了烘丝机影响因素及其排序,减少了产品质量波动;钟文焱等[11]采用多元回归分析等方法研究了松散回潮机加水比例调整方案,提高了烘丝机入口含水率稳定性。但上述研究或分析中,制丝设备优化方法仅考虑了设备因素对工艺参数的影响,工艺参数优化方法则忽略了可调参数对其他关键参数的影响,两种方法均未整体考虑多因素对关键参数的影响,因此仍难以保证工艺参数和卷烟质量的稳定性。为此,基于贝叶斯网络分析方法,构建了以工艺参数为节点、影响关系为路径、影响大小为路径参数的网络模型,并采用昆明卷烟厂制丝线MES 数据对模型进行验证,通过分析可调参数与关键参数的关系,以期为实现制丝工艺过程整体稳态优化提供支持。
1 网络模型构建
1.1 问题分析
制丝生产中因受设备老化、来料质量波动和生产环境变化等因素影响,会导致制丝工艺过程经常发生变化。为保证卷烟质量稳定性,需要动态维护制丝生产最优工况与关键工艺参数的稳定性。制丝工艺过程稳态优化数学模型可表述为:

由于影响制丝工艺参数稳定性的因素较多,且各参数间相互影响,采用式(1)无法直观体现工艺参数间的复杂关系。为此,在式(1)基础上,采用连续型贝叶斯网络方法构建了制丝工艺过程网络模型,用于描述参数间的影响关系。改进后制丝工艺过程稳态优化数学模型为:
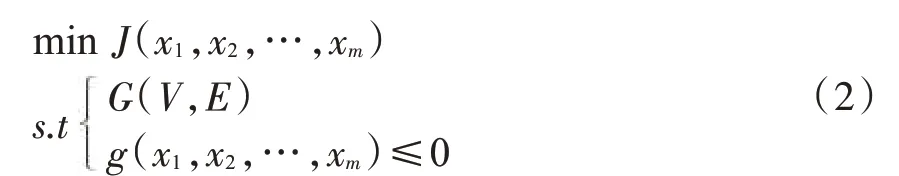
式中:G 为工业过程优化目标及其影响因素xi(i=1,2,…,m)所构建的有向无环图;V 为网络节点集合,即制丝工艺参数及其他影响因素;E 为有向图边权重表,表示可调参数或其他影响因素,与关键参数间是否存在显著影响以及影响规则。
1.2 构建流程
构建网络模型的关键是确定节点、边和边权重三要素。基于所采集的制丝工艺过程数据,利用机器学习分析方法,梳理网络节点集合,明确节点间的连接关系,计算连接的边权重。因此,网络模型构建可分为四大步骤,流程见图1。

图1 制丝工艺过程连续型贝叶斯网络模型构建流程图Fig.1 Flowchart of establishment of continuous Bayesian network
第一步:网络节点集合构建。基于网络模型分析目标和制丝生产经验,综合考虑数据的相关性,确定工艺参数和其他影响因素作为网络模型节点集合,且网络模型节点与工艺参数和其他影响因素相对应。
第二步:初步构建网络结构。确定网络节点集合后,采集网络节点数据,计算两节点间距离矩阵的协方差,用于描述两参数间的相似度,根据设定的置信度水平(5%)确定节点间的边(连接关系),实现网络模型的初步构建。两节点间距离矩阵协方差计算公式为:
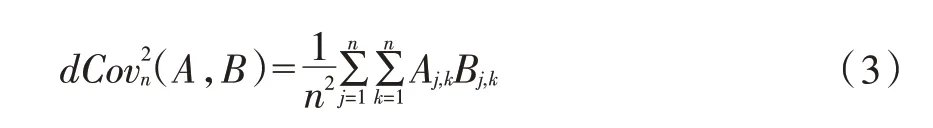
第三步:优化网络结构。初步网络中的边集合仅考虑了两节点间的关系,边方向不明确且存在冗余边,不利于表达可调参数与关键参数间的整体关系。为此,采用最大最小爬山法[12]进行网络优化。迭代过程中网络结构评分公式为:

式中:ScoreBIC为网络模型的贝叶斯信息量(Bayesian Information Criterion,BIC),用于网络模型评价;ScoreL为包含网络边方向的信息,网络模型边方向不同,其评分值也不同Dim[G]为网络结构复杂度惩罚值,用于简化网络间复杂度。
第四步:贝叶斯网络学习。针对网络中的每条边,采用最大似然估计法[1]计算网络参数:

式中:U 为节点的父节点集合;θ=〈β0,β1,β2,βk,δ〉;g(u[m])=(β1u1,…,βmum:θ)=∑βjuj+θ0为线性映射;u[m]表示包含其中一个节点及其所有父节点数据的第m 个实例数据;K[m]表示u[m]中某一个父节点的值。
基于式(3)分别对β0,β1,…,βk,δ 求偏导,得到(k+2)个等式。通过求解方程组,得到该边的条件概率参数β=〈β0,β1,…,βk,δ〉,经过不断迭代完成网络中所有边权重的计算,最终可确定网络模型的节点、边及其权重,实现网络模型构建。
2 实验验证
2.1 数据来源
以昆明卷烟厂“云烟”制丝线为对象采集生产过程MES 数据,采集时间为2017 年1 月1 日—12月31 日,合计取样1 431 批次,包括松散回潮工序、一级加料工序、二级加料工序共28 个工艺参数(可调参数22 个,关键参数6 个)。
根据昆明卷烟厂编制的《制丝工艺标准》维护制丝生产过程中部分工艺参数的稳定性,由于“云烟”配方调整、气候环境变化等原因,2017 年8 月24 日对《制丝工艺标准》进行了调整。为此,将调整前后的《制丝工艺标准》分别表示为标准A 和标准B,标准A 和标准B 分别对应的6 个关键参数设定值见表1。其中,将基于标准A 的MES 数据作为训练样本构建网络模型,分析可调参数与关键参数间的关系;将基于标准B 的MES 数据作为测试样本对网络模型进行验证,确定网络模型的可用性。

表1 制丝工艺标准关键参数设定值Tab.1 Values of key parameters set by technological standards for tobacco primary processing
2.2 网络模型构建
基于所采集的制丝工艺数据,确定网络模型的节点集合为松散回潮、一级加料、二级加料等工序的28 个工艺参数,利用网络模型构建方法,采用训练样本数据进行网络学习和训练,得到制丝工艺过程网络模型G(V,E)。其中,V 为含节点与边的网络模型拓扑结构,E 为路径参数。
2.2.1 网络模型拓扑结构(V)
训练得到的网络模型拓扑结构见图2。其中,松散回潮工序的出料含水率、出料温度,一级加料工序的出料含水率、出料温度,二级加料工序的出料含水率、出料温度为本实验中的6 个关键参数,其余22 个节点为可调参数。由图2 可见,拓扑结构中的边及边方向,可以直观描述工艺参数间的影响关系,并可将整个制丝工艺过程划分为松散回潮、一级加料、二级加料3 个子网络模型。
2.2.2 路径参数分析(E)
路径参数可以量化工艺参数间的影响关系,网络模型中6 个关键参数的路径参数分别见表2~表7。由表2 和表3 可见,松散回潮工序中物料累计量、汽水混合自动阀门开度、蒸汽自动阀门开度等与出料温度和出料含水率均呈正相关;加水比例与出料含水率呈正相关,与出料温度呈负相关。在松散回潮工艺参数调整时,可重点考虑上述4 个可调参数的影响。
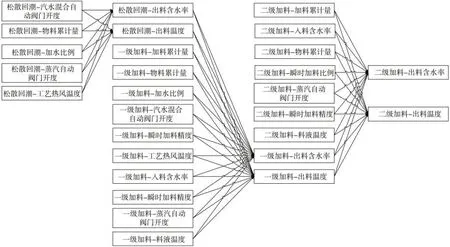
图2 制丝工艺过程网络模型结构图Fig.2 Structure of network for technological process in tobacco primary processing

表2 松散回潮-出料含水率影响因素及权重①Tab.2 Influencing factors of moisture content in output tobacco after loosening and conditioning and their weights

表3 松散回潮-出料温度影响因素及权重Tab.3 Influencing factors of output tobacco temperature after loosening and conditioning and their weights
由表4 和表5 可见,一级加料工序中加料累计量对出料含水率和出料温度均呈显著正相关,物料累计量对出料含水率和出料温度均呈显著负相关,加水比例与出料含水率呈正相关,但是与出料温度呈负相关。松散回潮工序中出料含水率、出料温度对一级加料-出料含水率的影响占比为16.57%>10%,对一级加料工序中出料温度的影响占比为6.89%>5%。因此,在一级加料工序中应考虑松散回潮对生产的影响。
由表6 和表7 可见,二级加料工序中加料累计量、物料累计量、入料含水率、瞬时加料比例、蒸汽自动阀门开度对出料含水率、出料温度有较大影响。其中,加料累计量、入料含水率等与出料含水率、出料温度均呈正相关,物料累计量、瞬时加料比例等与出料含水率、出料温度均呈负相关。在二级加料工艺参数调整时,可重点考虑上述5 个可调参数的影响。一级加料工序中出料含水率、出料温度对二级加料工序中出料含水率的影响占比为17.59%>10%。因此,在二级加料工序中应考虑一级加料对生产的影响。

表4 一级加料-出料含水率影响因素及权重Tab.4 Influencing factors of moisture content in output tobacco after primary casing and their weights

表5 一级加料-出料温度影响因素及权重Tab.5 Influencing factors of output tobacco temperature after primary casing and their weights

表6 二级加料-出料含水率影响因素及权重Tab.6 Influencing factors of moisture content in output tobacco after secondary casing and their weights
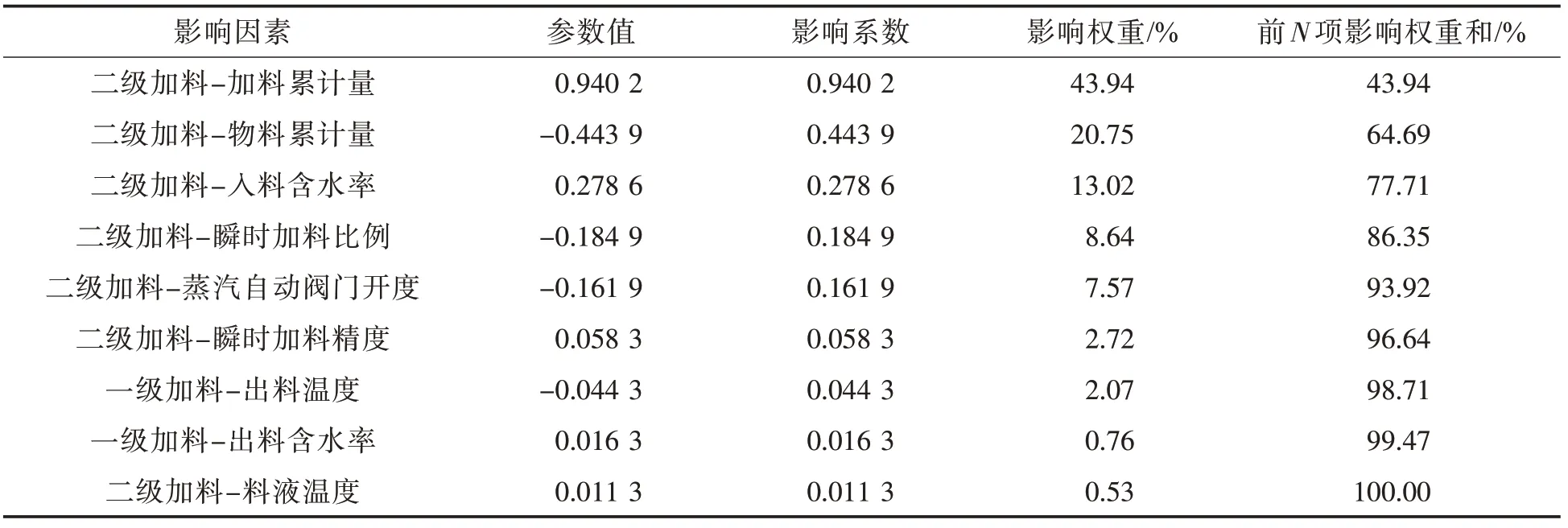
表7 二级加料-出料温度影响因素及权重Tab.7 Influencing factors of output tobacco temperature after secondary casing and their weights
2.3 网络模型验证
采用标准B 生产的MES 数据作为测试样本,对比分析测试样本中6 个关键参数的预测值与真实值,对网络模型的准确性及适应性进行验证,结果见表8。可见,6 个关键参数的网络模型预测值与真实值偏差均在1%以内,平均偏差为0.521 7%,低于标准B 中相应关键参数设定区间中心值与真实值间的平均偏差0.853 6%,表明网络模型预测结果具有较高的准确度,能够较好地描述制丝工艺参数与质量指标间的影响关系。

表8 网络模型预测值与真实值对比Tab.8 Comparison between real values and the values predicted by network model
3 结论
基于连续型贝叶斯网络研究了制丝工艺过程的稳态优化,通过所构建的网络模型分析了制丝过程中可调参数与关键参数间的影响关系。以昆明卷烟厂“云烟”制丝线松散回潮、一级加料、二级加料工序共28 个工艺参数为对象进行测试,结果表明:关键参数的网络模型预测值与真实值间的偏差均在1%以内,平均偏差小于真实值与工艺标准设定值平均偏差,表明网络模型预测具有较高的准确性,也证明基于连续型贝叶斯网络所建立的制丝过程稳态优化方法,能够应用于制丝工艺标准制修订以及工艺参数的调整。
