考虑钢轨轴向温度力的无砟轨道振动响应分析*

2019-12-28刘林芽秦佳良

城市轨道交通研究 2019年12期

宋瑞刘林芽秦佳良

(1.南昌工程学院土木与建筑工程系，330029，南昌；2.华东交通大学铁路环境振动与噪声教育部工程研究中心，330013，南昌//第一作者,教授)

0 序言

随着我国高速铁路的飞速发展，轨道结构的动力响应分析已经成为铁道工程领域中十分重要的研究方向[1]。而且随着列车速度的不断提高，对轨道线路的平顺性要求也越来越高。无缝线路因为减少了钢轨接头，具有列车行驶平稳性好、线路养护维修费用低和使用寿命长等优点，目前已经广泛应用于铁路和城市轨道交通的轨道结构中。

文献[2]对轨道结构的动力响应做了大量研究，提出和建立了多种车辆-轨道耦合模型[2-9]。这些模型的共同特点是程序设计比较复杂，且并不能考虑钢轨轴向温度力的作用。但由于无缝线路限制了钢轨的轴向自由伸缩，在环境温度发生变化时，钢轨内部会产生较大的轴向力,因此在实际运营过程中，钢轨内部存在着较大的温度力作用[10]。钢轨轴向温度力的作用对无砟轨道的振动响应的影响亟待研究。

文献[11-13]提出了应用傅里叶变换法分析轨道结构振动响应的方法。该方法适用于任何复杂的轨道结构动力学问题，且易于编制程序,但并未考虑钢轨轴向温度力的影响。因此本文在此基础之上，将钢轨模拟成Timoshenko梁，并考虑钢轨轴向温度力的作用，采用傅里叶变换法来计算轨道结构的振动响应。首先建立了考虑钢轨轴向温度力作用的轨道振动微分方程，并对其进行傅里叶变换，求解傅里叶变换域中的振动位移;再通过傅里叶逆变换便可得到轨道结构的振动响应，最后分析了钢轨轴向温度力作用对无砟轨道振动响应的影响。

1 无缝线路钢轨轴向温度力计算

当轨温发生变化而产生自由伸缩时，钢轨的伸缩量为：

Δl=αlΔt

(1)

式中:

Δl——钢轨的伸缩量；

α——钢轨的线膨胀系数；

l——钢轨长度；

Δt——轨温变化幅度，又称轨温差。

如果轨温发生变化，钢轨受到阻力完全不能伸缩，将长为l的钢轨产生的Δl转化为温度应力，由胡克定律可得到钢轨的温度应力σt为：

(2)

式中:

E——钢的弹性模量；

εt——钢轨的温度应变。

当α取0.011 8×10-3/℃，E取2.1×105MPa时,可算得σt和钢轨的温度力Nt：

σt=2.48Δt

(3)

Nt=σtA=2.48ΔtA

(4)

式中，Δt单位取℃；σt单位取MPa；Nt单位取N；A为钢轨的截面面积，单位取mm2。

由式(4)可知，长钢轨中的Nt只与Δt有关，而与l无关，这也是发展跨区间无缝线路的理论依据。因此，控制长钢轨中Nt的大小的关键是控制Δt。我国各地区的最大轨温差可达到100 ℃，所以本文在计算Nt时考虑最大升温幅值为50 ℃，最大降温幅值为50 ℃。

2 无砟轨道结构连续弹性三层梁模型

将无砟轨道结构简化为连续弹性三层梁模型，其中,钢轨采用Timoshenko梁模拟，并考虑钢轨轴向温度力的作用，轨道板和底座板采用Euler梁模拟。图1所示为无砟轨道结构连续弹性三层梁模型。

图1 无砟轨道结构连续弹性三层梁模型

该模型的振动微分方程为：

(5)

(6)

ks(z-y)-kr(w-z)=0

(7)

khy-ks(z-y)=0

(8)

式中:

N——钢轨的轴向温度力；

ρ——钢轨的密度；

θ——钢轨的转角；

G——钢轨的剪切模量；

K——剪切系数；

A——钢轨的横截面面积；

w，z，y——分别为钢轨、轨道板、混凝土支撑层的竖向扰度；

δ——Dirac函数；

x——沿轨道方向的距离；

t——时间；

v——列车运行速度；

Fj——第j个轮对轴重的一半；

mj——第j个车轮的质量；

aj——t=0时第j个轮对距原点的距离；

n——轮对总数；

η——轨道随机不平顺值。

3 求解轨道结构振动微分方程的傅里叶变换法

对式(5)～(8)作傅里叶变换，则有：

-mrω2W0+(GAK+N)β2W0-iGAKβφ0+

iωcr(W0-Z0)+kr(W0-Z0)=F0

(9)

-ρIrω2φ0+ErIrβ2φ0+GAKφ0+iGAKβW0=0

(10)

EsIsβ4Z0-msω2Z0+iωcs(Z0-Y0)-

jωcr(W0-Z0)+ks(Z0-Y0)-kr(W0-Z0)=0

(11)

EhIhβ4Y0-mhω2Y0+iωchY0-iωcs(Z0-Y0)+

khY0-ks(Z0-Y0)=0

(12)

式中：

W0,F0,φ0,Z0,Y0——分别为变量对应的幅值；

ω——振动角频率；

β——振动波数。

联立求解式(9)～(12)，可得到：

W(β)=[cd-(iωcs+ks)2]F0/

{(iωcr+kr)[cde-c(iωcr+kr)-f(iωcs+ks)2]}

(13)

φ(β)=aW(β)

(14)

Z(β)=fW0-F0/(iωcr+kr)

(15)

Y(β)=(iωcs+ks)/c·Z0(β)

(16)

其中，a，b，c，d，f分别为计算数值，具体数值可参考文献[13]。

将式(13)～式(16)代入式(9)～(12)中，并进行傅里叶逆变换，得到：

wf(x,t)=Wf(x,t)ei(φw+Ω t)

(17)

φf(x,t)=Φf(x,t)ei(φφ+Ω t)

(18)

zf(x,t)=Zf(x,t)ei(φz+Ω t)

(19)

yf(x,t)=Yf(x,t)ei(φy+Ω t)

(20)

其中，φw,φφ,φz和φy分别为复数wf(x,t),φf(x,t),zf(x,t)和yf(x,t)的相位角;Ω为荷载激振频率。

根据式(17)～(20)可以求得钢轨、轨道板和混凝土支撑层的速度、加速度，以及作用于轨道板、混凝土支撑层和路基上的动压力。

4 考虑钢轨轴向温度力的无砟轨道振动响应分析

应用上述模型，利用MATLAB软件编制相应的程序，对考虑钢轨轴向温度力的CRTSⅡ型板式无砟轨道结构进行振动响应分析。CRTSⅡ型板式无砟轨道的相关结构参数如表1中所示。考虑列车为8节编组的CRH3型动车，速度取300 km/h，线路不平顺模拟成美国六级不平顺。Δt分别取-50 ℃、0 ℃、50 ℃时，将其产生的温度力加载在钢轨轴向，然后分析其对无砟轨道结构振动响应的影响。

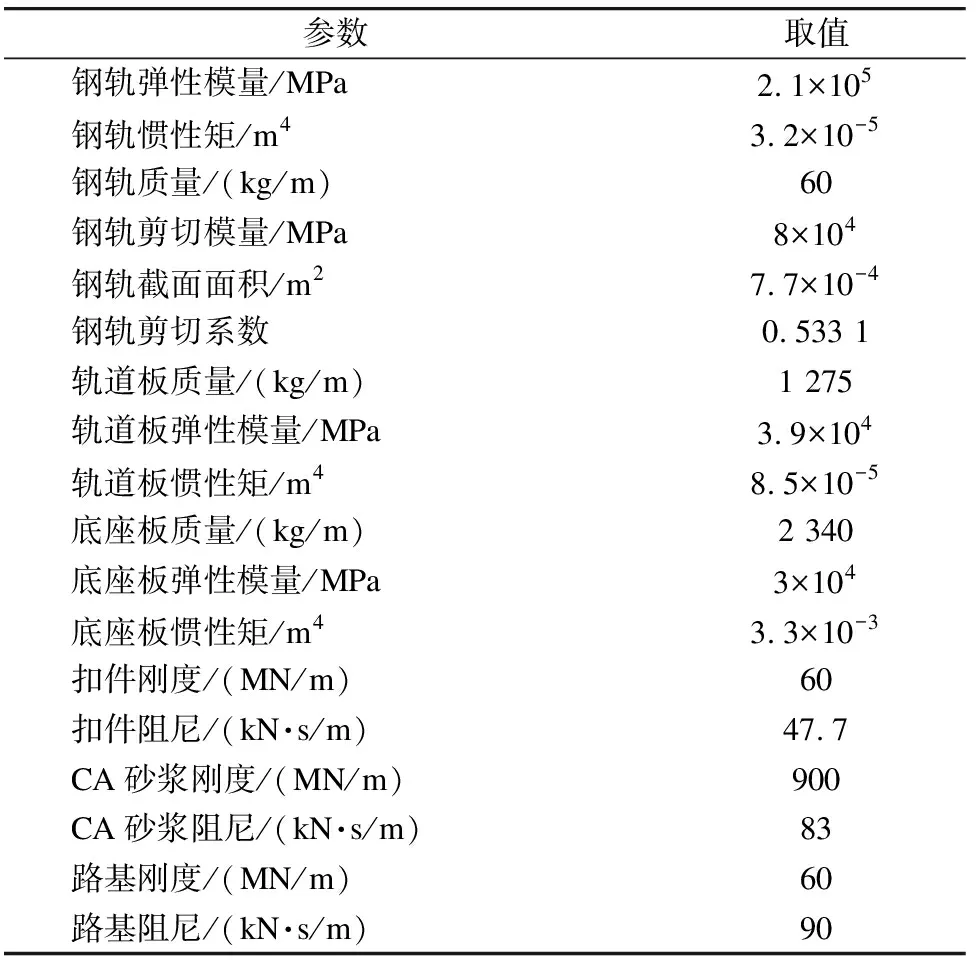
表1 CRTSⅡ型板式无砟轨道结构参数

不同Δt下钢轨、轨道板及底座板的位移和振幅如表2～4所示。不同Δt下单位长度的轨道板、底座板和路基的动压力如图2所示。

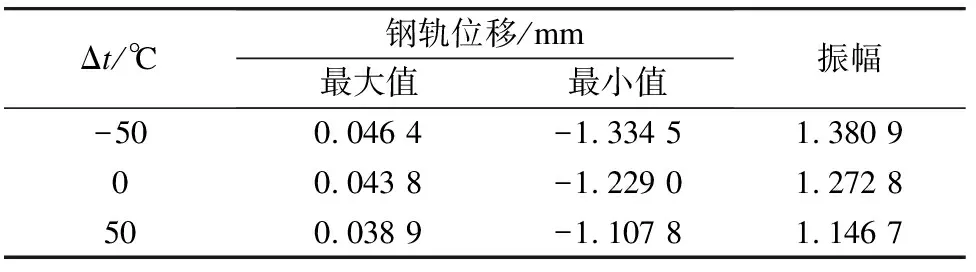
表2 不同Δ t条件下的钢轨位移和振幅

表3 不同Δ t条件下的轨道板位移和振幅

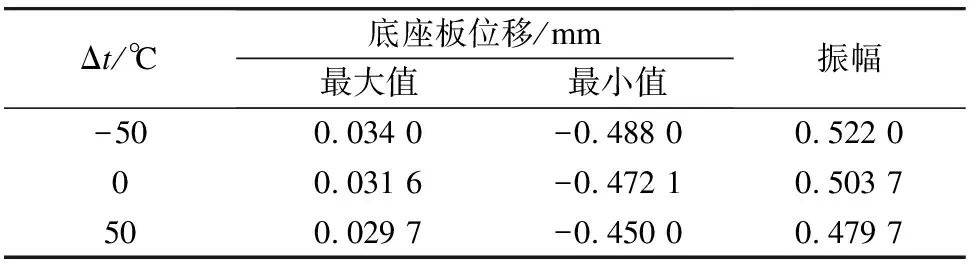
表4 不同Δ t条件下的底座板位移和振幅

图2 Δt对轨道动压力的影响曲线

由表2～4可知，Δt越大，即钢轨所受的轴向温度力越大时，钢轨、轨道板和底座板的位移都有不同程度地降低，且钢轨位移的降低幅度比轨道板和底座板要大。当Δt为50 ℃时，钢轨位移降低约10%，轨道板位移降低约8%，底座板位移降低约5%。

由图2可知，轨道板、底座板和路基的动压力与Δt基本成线性关系，而且Δt越大时，轨道的动压力却越小。轨道板和底座板的动压力的降低幅度比路基要大。当Δt为50 ℃时，轨道板和底座板的动压力降低约10%，路基动压力降低约8%，底座板动压力降低约5%。这是由于钢轨受到轴向压力作用时，钢轨的振动响应会减小，同时传入下部轨道结构的能量亦会随之减小，因此轨道板、底座板和路基的振动响应也会减小。