一种零纹波高增益DC/DC变换器仿真实验分析

王攀攀，段 森，童志刚，于东升，许允之，韩 丽

一种零纹波高增益DC/DC变换器仿真实验分析

王攀攀，段 森，童志刚，于东升，许允之，韩 丽

（中国矿业大学 电气与动力工程学院，江苏 徐州 221116）

为解决传统Boost电路升压能力不足、输入电流纹波大的问题，提出一种基于耦合电感的新型DC/DC变换器。在变换器的前级将耦合电感和电容相结合，实现零输入电流纹波；在变换器的后级利用耦合电感倍压单元扩展变换器的电压增益；引入二极管+电容的箝位电路，用以抑制漏感带来的电压尖峰，进而形成新的变换器拓扑结构。依据电路理论分析了变换器的工作原理和工作特性，并以光伏发电系统中的直流升压环节作为应用背景，在Simulink仿真平台上进行了实验验证和分析。实验结果表明：该变换器具有高电压增益、零输入纹波和低电压应力的特点。

DC/DC变换器；耦合电感；仿真实验

在以光伏电池板、燃料电池构成的发电并网技术中，具有高电压增益的DC/DC变换器必不可少[1-3]。目前提高变换器升压能力的方法主要有：（1）采用输出串联结构[4]实现电压的叠加，但是该方法需要较大的电容来降低输出电压纹波；（2）通过变换器级联的方式提高增益，电路的输出增益为各级升压比之积，但是其效率较低[5-6]；（3）采用开关电容结构，开关电容在充电阶段为并联，在放电阶段为串联，通过增加开关电容的个数即可实现较高的电压增益，该方法在电容充放电过程中容易产生电流尖峰[7-9]；（4）采用 耦合电感结构，形成一个额外的电压源串联在电路 中[10-11]，该方式结构简单、易于实现，但是随着升压倍数和耦合电感变比的增加，其输入电流纹波也随之增大，降低了光伏电池板和燃料电池的发电效率，也缩短了它们的使用寿命[12]。

本文提出了一种基于耦合电感的具有高电压增益、零纹波特性的新型DC/DC变换器，并利用Simulink对该变换器进行仿真实验，以验证其可行性和优越性。该变换器的设计、分析和实验过程应用于教学，可加深学生对直流升压变换器电路结构和工作原理的理解，提高他们分析问题和解决问题的能力。

1 零纹波、高增益DC/DC变换器拓扑设计

传统Boost电路的电压增益为1/(1–)，其中为占空比。根据该式可知，只要改变占空比，即可实现任意升压比。但是，由于受到电路本身寄生参数的影响，当占空比大于一定值时，其升压能力大大下降，无法实现高升压比。此外，过大的占空比，将使输出二极管的导通时间很短，电流峰值过大，造成严重的反向恢复损耗和EMI问题。

为了扩展变换器的电压增益，在传统Boost电路的基础上，增加一个基于耦合电感的倍压单元，从而形成如图1所示的高增益升压电路。

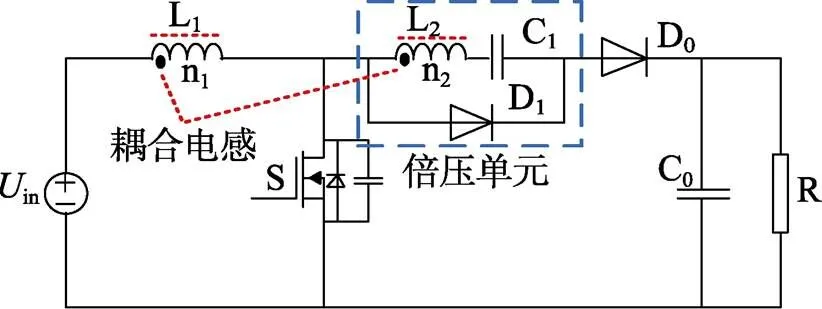
图1 含耦合电感倍压单元的Boost电路

该变换器的工作过程可分为2个阶段。当开关管S导通时，耦合电感的励磁电感和倍压电容C1储存能量，输出电容C0向负载供电；当开关管关断时，输入电源、耦合电感和倍压电容串联共同向负载供电，实现更高电压的输出。该变换器的电压增益为(1+1)/ (1–)，其中1为耦合电感的原副边匝比。

可以看出：具有倍压单元的Boost电路的升压比不但可以通过占空比进行调整，还与耦合电感原副边匝比有关，因此可以在较小占空比下通过调整匝比来实现高升压比的目的。但是该变换器的输入电流存在纹波，影响了光伏电池板、燃料电池等电源的发电效率和使用寿命，开关管还会受到耦合电感漏感的影响，承受较高的电压应力。

针对上述变换器的问题，在图1的基础上，利用1个二极管和1个电容构成箝位电路，解决漏感带来的尖峰电压问题。然后，将耦合电感与电容相结合，构建纹波抑制单元，实现输入电流的零纹波。基于该思路，设计了一种具有低电压应力、零输入电流纹波、高增益的DC/DC变换器，其具体拓扑结构如图2所示。

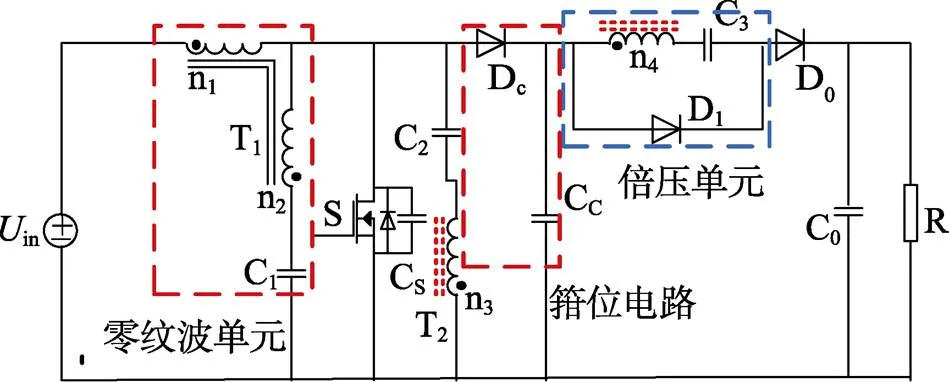
图2 新型DC/DC变换器拓扑

图2中，耦合电感T1与电容C1是零纹波单元；二极管Dc与电容Cc构成了箝位电路；耦合电感T2、电容C3和二极管D1构成了倍压单元。

2 DC/DC变换器工作模态分析

为了便于分析，将DC/DC变换器中的耦合电感等效为理想变压器与励磁电感并联，再与漏感串联，如图3所示。其中耦合电感T1的匝比为1(1∶2)，耦合电感T2的匝比为2(3∶4)。对变换器的工作原理进行分析需作如下假设：（1）电路拓扑中所含元件均为理想型器件；（2）各电容足够大，电容电压稳定。

图3 新型DC/DC变换器的等效电路

变换器在稳态时，主要元器件的电压和电流在一个开关周期内的变化规律如图4所示。根据电流变化的特点，可将变换器的工作状态分为5个工作模态。

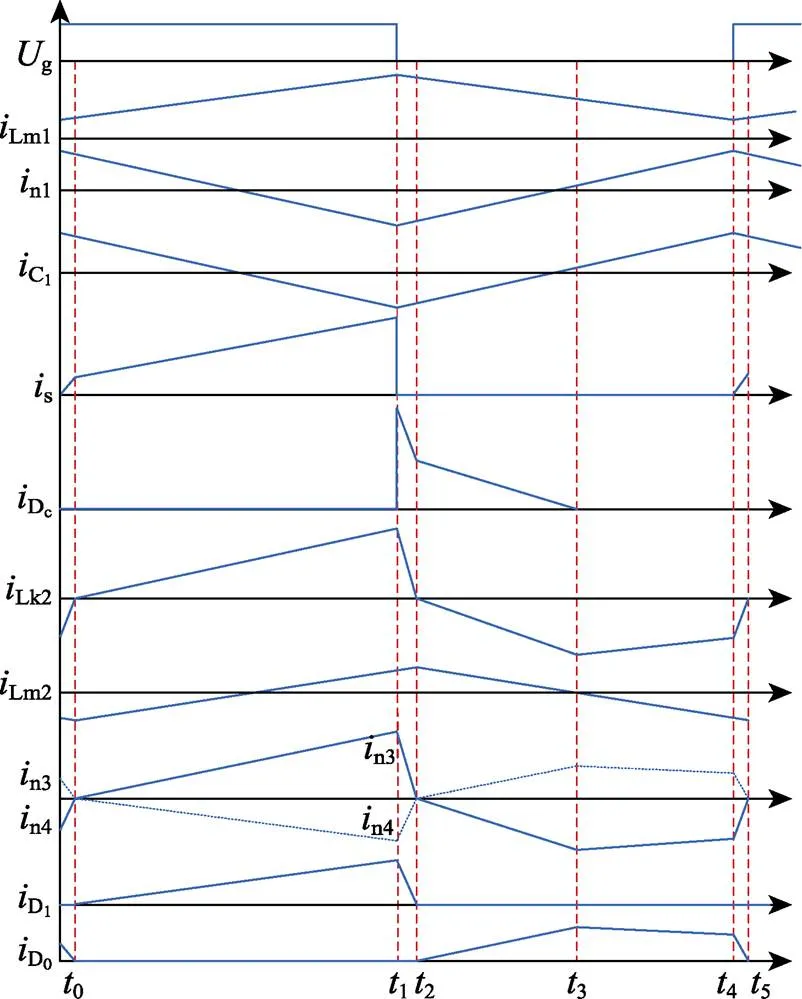
图4 主要元器件电压电流变化规律

（1）模态1（0—1）对应的各回路如图5所示。开关管S导通，T1励磁电感Lm1在输入电源的作用下储能，其电流Lm1线性增加；电容C1先被耦合电感T1副边充电，直到其两端电压C1=1n1，然后又通过S放电，因此C1、n1一直下降。箝位二极管Dc的阳极通过S与电源负极相连，因此处于关断状态；同时，C2—S—Lk2构成回路，C2放电，Lk2、Lm2上升。由于T2原边绕组n3的同名端与C2的正极相连，因此n4的同名端为正，n4—D1—C3构成回路，副边n4通过D1给C3充电，以至C3=n4=2n3=2C2；在此种情况下，输出二极管D0的阳极通过D1与箝位电容Cc相连，阴极与输出电容C0相连，由于C0高于Cc，因此D0关断，只有输出电容C0给负载供电。

在该模态中，T1漏感Lk1两端的电压为－n1，且n1=n2/1=C1/1，因此流过该漏感的电流为

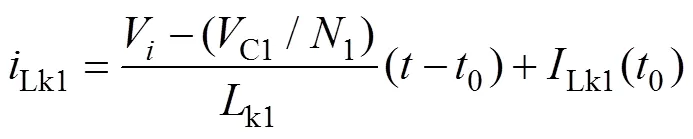
（2）模态2（1—2）对应的各回路如图6所示。在1时刻，开关管S关断。T1励磁电感Lm1释放能量，Lm1下降，T1同名端电压为负，Dc阳极电压等于输入电压与励磁电感电压之和，因此Dc导通。T2漏感Lk2中储存的能量通过Dc向Cc释放，漏感电流Lk2迅速减小。此时，Lm2仍上升，T2同名端电压仍为正，因此二极管D1仍导通，D0仍关断。在2时刻n4下降到零，因此D1在2时刻实现零电流关断，但D0仍为关断状态。此模态中由于Dc的导通，使得漏感Lk2中存储的能量能够向Cc释放，同时开关管两端电压也被箝位在Cc，从而避免了因漏感带来的尖峰电压，减小了S的电压应力。

图6 模态2

（3）模态3（2—3）对应的各回路如图7所示。开关管S和二极管D1处于关断状态，箝位二极管Dc仍处于导通状态；电流Lm1、Lm2因磁能的释放而逐渐下降，导致T1、T2同名端电压均为负。输入电源电压、T1原边电压、T2副边电压和倍圧电容电压串联叠加，使得D0阳极电位高于阴极，D0导通。输入电源的能量和耦合电感T1、T2，以及倍压电容中存储的能量共同向负载侧供电，Lm1、n4皆为正，C0被充电。

在该模态中，Lk1两端的电压可表示为：Lk1=0－C3－n4－n1－，又因n2=1n1=0－C3－n4－C1，于是流过漏感k1的电流为：

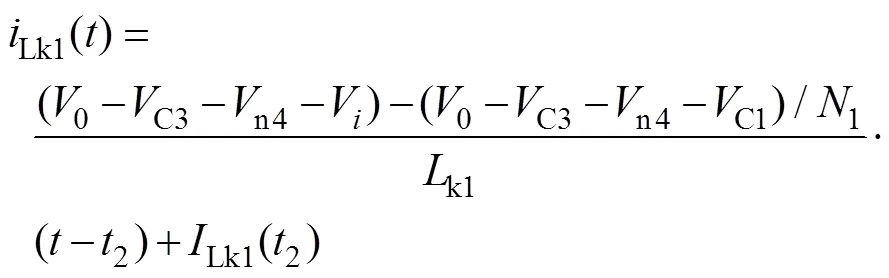
（4）模态4（3—4）对应的各回路如图8所示。在3时刻，Lm2下降到零，Lm2能量释放完毕，此后Lm2开始反向增大，Lm2开始储能；而Lk2开始减小，导致漏感Lk2两端电压反向，使得Dc阳极电位低于阴极，因此Dc处于关断状态；其他开关器件状态不变。此时，电容Cc和倍压单元继续向负载侧供电。

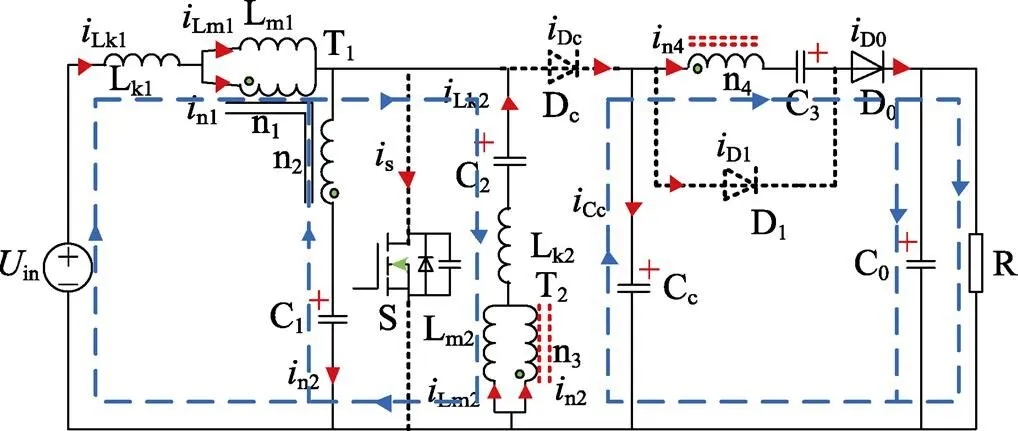
图8 模态4

（5）模态5（4—5）对应的各回路如图9所示。在4时刻，开关管S导通信号来临，n3在C2的作用下减小，因此n4也开始减小，并在5时刻，n4下降到零，二极管D0实现零电流关断，此后新的周期 开始。

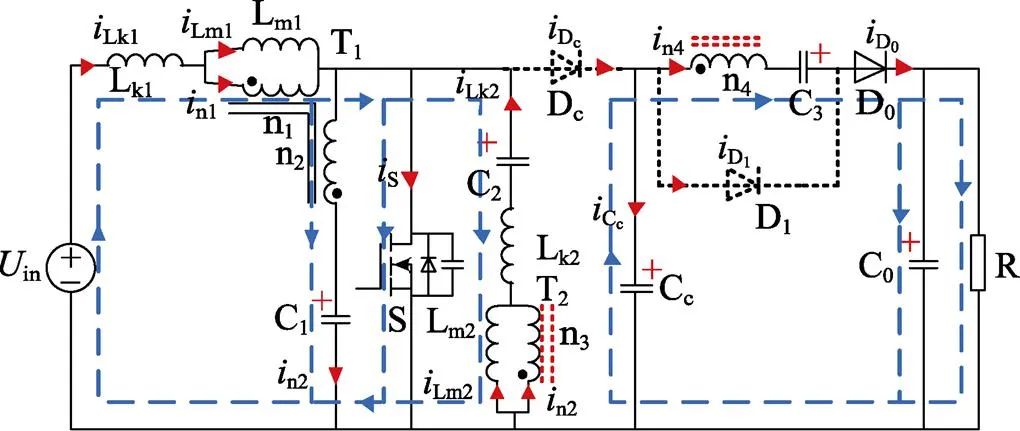
图9 模态5

3 变换器的工作特性分析

在进行变换器性能分析时，忽略了电路损耗，且其中的器件同样满足第2节中的假设。当变换器处于稳态运行时，由于电感电压在一个开关周期内的平均值为零，因此可得到如下关系式：

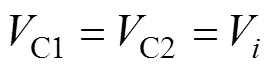
3.1 电压增益分析

为简化增益计算过程，忽略了T2漏感的影响，并且只考虑开关管导通时励磁电感Lm2储能和开关管关断时Lm2放能这两个过程。

当开关管S导通时，由于D1导通，Dc和D0关断，则C2—S—Lm2构成回路，Lm2上的电压为

当开关管S关断时，由于Dc和D0导通，D1关断，C2—C3—R构成回路，且C3=2C2，则Lm2上的电 压为

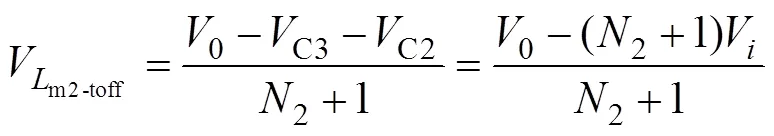
根据电感的伏秒平衡原理，Lm2-ton·on=Lm2-toff·off（on和off分别为开关管导通和关断的时间），可以计算出本文提出的变换器的电压增益为

式中：为占空比，=on/(on+off)。

从式（6）可以看出：新型变换器的电压增益不但与占空比有关，还与耦合电感的匝数比有关，一旦将匝比设计得较大，即可实现较高的升压比。

3.2 零输入电流纹波分析

根据电路原理可知，输入电流即为漏感Lk1的电流，即in=Lk1。为简化分析，只考虑模态1和模态3。欲使输入电流的纹波为零，则需要使Lk1在模态1和3中的变化率为0，即dLk1/d=0。

在模态1中，根据式（1）和式（3）可得：

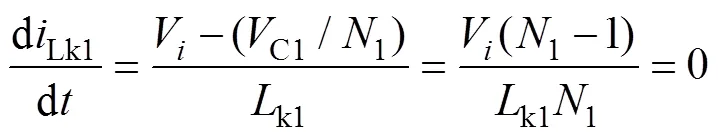
同理Lk1在模态3中，需要满足：

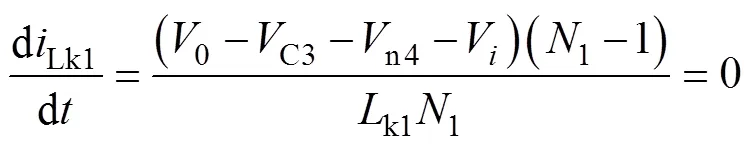
分析式（7）和式（8）可知：在开关管S导通和关断过程中实现输入电流零纹波的条件是一致的，即：1=1。

3.3 电压应力分析

由于在开关管S两端引入了箝位电路，因此在分析其电压应力时，可不计耦合电感T2漏感的影响。当开关管S关断时（如模态3），S两端的电压为S-stress=C2+Lm2=Cc。将式（5）代入该式，可得开关管S的电压应力为

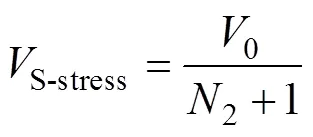
在模态3中，出现续流二极管D1的最大反向电压D1-stress，D1-stress=0－Cc。将式（5）和Cc=Lm2+C2的关系代入其中，可得续流二极管D1的电压应力为

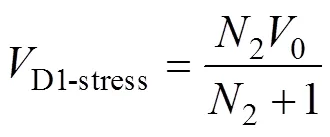
由模态1可知，箝位二极管Dc在关断时，阳极与Cc负极相接，阴极与Cc正极相接，因此其两端承受的最大反向电压为Dc-stress=Cc，与开关管的电压应力一样。同理，输出二极管D0的电压应力D0-stress=0－CcD1-stress。

可以看出，各个开关器件的电压应力都比输出电压值小，因而为变换器的低功耗、低成本奠定了基础。

4 仿真实验

4.1 电路参数设计及仿真模型搭建

以光伏发电系统为例，将DC/DC变换器应用于直流升压环节，如图10所示。

图10 基于并联直流模块的光伏系统

图10中，高增益DC/DC变换器是光伏电池板与逆变器之间的桥梁，须同时满足两者的需求。由于单个光伏组件的输出电压为50 V左右，输出功率约为300 W；而单相并网逆变器所需的直流电压又为380 V，因此将DC/DC变换器的输入电压确定为50 V，期望的输出电压为380 V，输出功率为360 W。

为实现零纹波，依据3.2节推导出的匝比条件，设置耦合电感T1的匝比1=1。耦合电感T2的匝比对变换器的电压增益和器件的电压应力均有较大影响，根据电压增益公式（8），可以得到T2匝比2：

2=0(1－)/V－1

在DC/DC变换器的控制中，理想的占空比通常为0.4~0.7。如果占空比设为0.6，则T2的匝比可选2。

电路中各电容的选择主要考虑电压应力和电压纹波，计算公式为

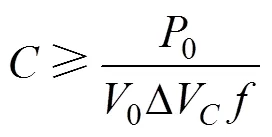
式中：0为输出功率，0为输出电压，Δc为电容上的电压纹波，为开关频率。将电容的电压纹波设定为电容电压的1%，如果开关频率为50 kHz，则1=2= 37.8 μF，3=18.9 μF，c=14.8 μF，考虑一定的裕量，最终选择1=2=47 μF，3=c=22 μF。此外，为了让变换器输出电压的纹波尽可能小，提高输出电压的质量，0可选较大值。

综合上述的设计与计算，满足本实验的直流变换器参数如表1所示。

基于零纹波、高增益DC/DC变换器的拓扑结构，结合所设计的电路参数，在Simulink环境下搭建升压电路的仿真模型如图11所示，该仿真模型可用于指导实物设计[13-16]。

表1 DC/DC变换器电路参数

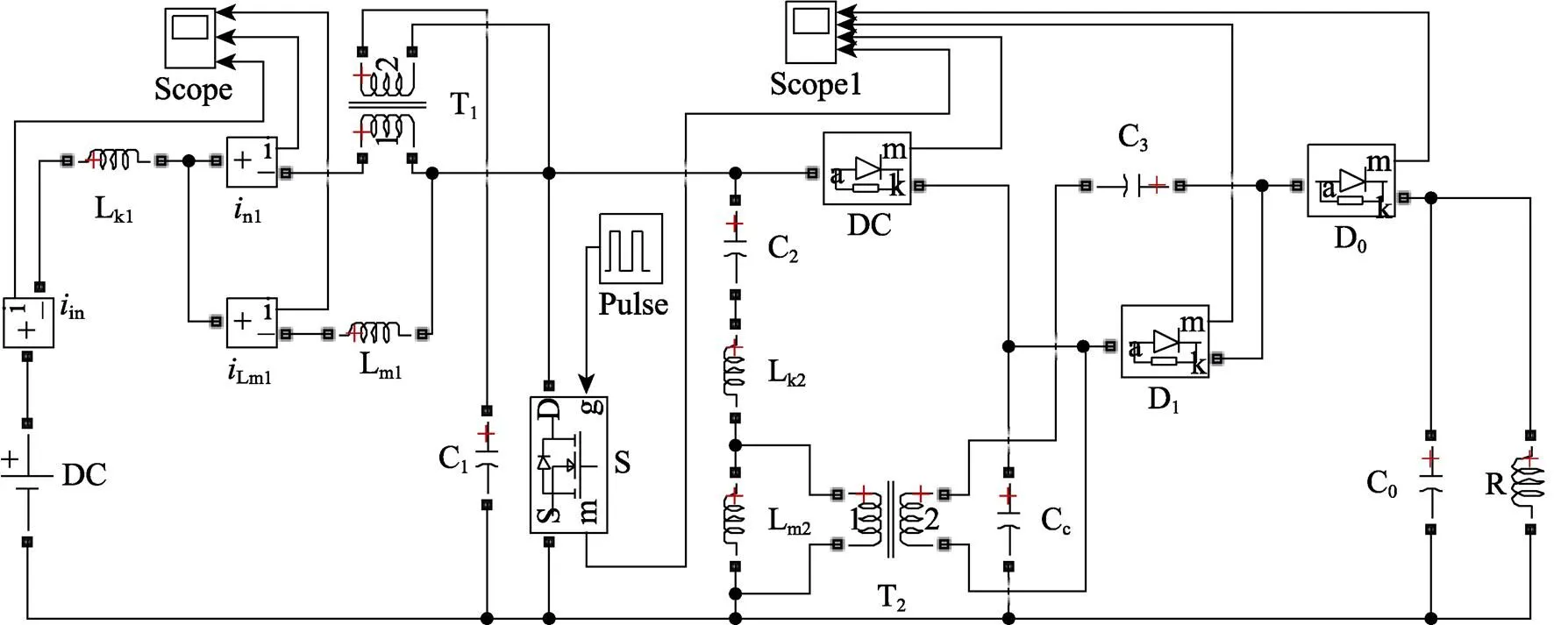
图11 新型DC/DC变换器仿真电路模型

4.2 实验验证分析

4.2.1 电压增益验证分析

在表1参数的条件下，将开关管驱动信号占空比设置为0.6，对零纹波、高增益DC/DC变换器进行仿真实验。实验输出电压380 V，与理论计算值一致，波形如图12所示。此时的升压比达到了7.6倍，远远高于传统Boost变换器在该占空比下的升压能力，验证了该DC/DC变换器的高增益的特性。

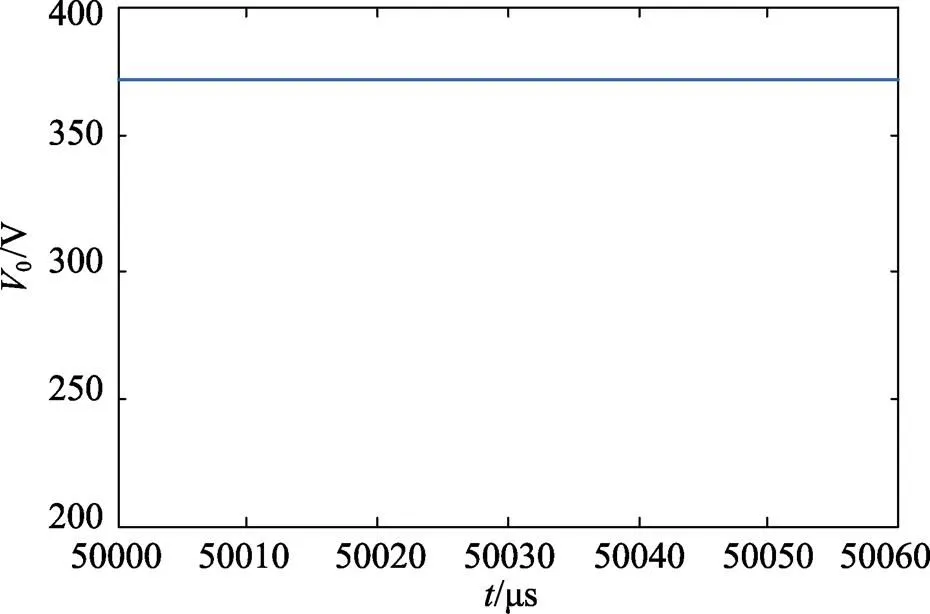
图12 输出电压波形

4.2.2 零输入电流纹波验证分析

分别测量了输入电流、励磁电感Lm1电流和T1原边n1电流，如图13所示。从图中可见，输入电流in几乎没有任何波动。这是因为励磁电感电流Lm1上升/下降时，T1原边电流n1下降/上升，且两者上升或下降的斜率也相等，实现了互相补偿，从而消除了输入电流的纹波。

图13 iin、iLm1、in1波形

耦合电感T1的匝比是影响输入纹波的另一个因素。为了与图13的结果进行比较，此处设置1为1.03，即不满足零纹波条件，其仿真结果如图14所示。从图中可见，由于T1的原副边匝数不再相等，Lm1上升或下降的斜率与n1下降或上升的斜率也不再相等，无法完全抵消，从而导致输入电流有较大的脉动。

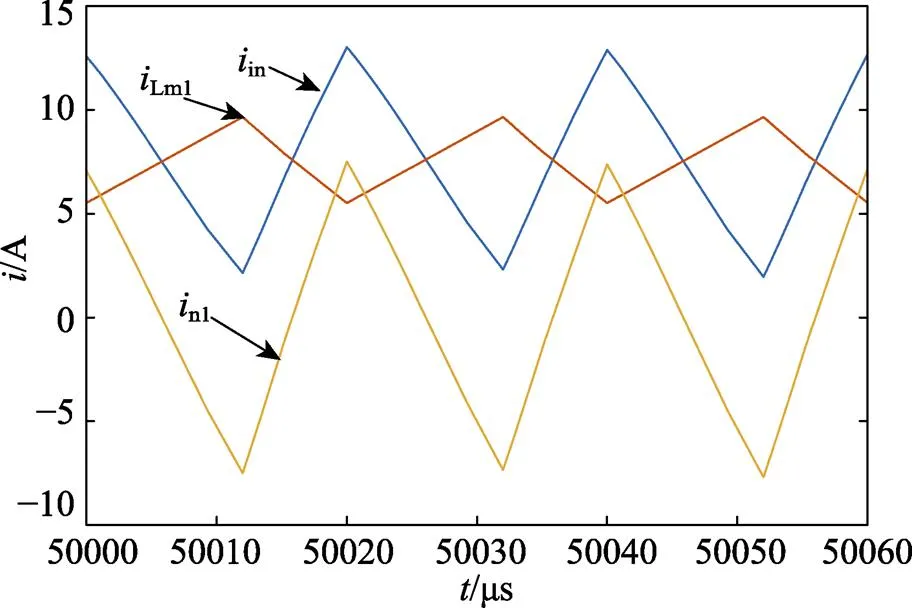
图14 N1不等于1时的iin、iLm1、in1波形

4.2.3 开关器件电压应力验证分析

图15为开关管两端的电压波形。可以看出：开关管在关断期间所承受的电压应力约为126.6 V（与3.3节理论计算值一致），远小于输出电压380 V，这为选择低导通损耗的开关管创造了条件。

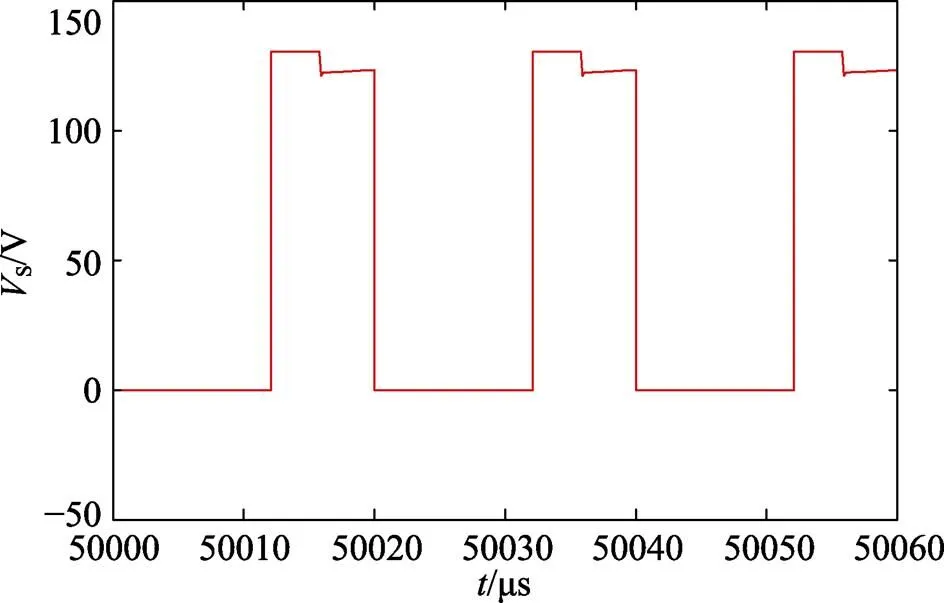
图15 开关管S两端的电压波形

此外，实验结果显示Dc电压应力约为126.6 V，D1、D0电压应力相同，约为253.3 V，与理论分析一致，且所有二极管的电压应力均小于输出电压，这有利于提高变换器的效率，降低器件成本。

5 结语

高电压增益、零输入电流纹波和低电压应力新型变换器的研究过程（包括变换器的设计、原理与性能的分析，以及仿真实验的验证）包含大学生科研训练中发现问题和分析、解决问题的各个环节，将其作为一个案例进行实验教学，不但可以加深学生对DC/DC变换器拓扑结构和工作原理的理解，还有助于挖掘学生的创新潜力，提高学生自主学习、独立思考和分析问题、解决问题的能力。

[1] 屈克庆，梁晓霞，赵晋斌，等.一种带有泵升电容的新型高增益升压直流变换器[J].电力系统自动化，2014, 38(19): 102–107.

[2] TUMMURU N R, MISHRA M K, SRINIVAS S. Dynamic energy management of hybrid energy storage system with high–gain PV converter[J]. IEEE Transactions on Energy Conversion, 2015, 30(1): 150–160.

[3] 高伟，罗全明，吕星宇，等.一种三绕组零纹波高增益DC/DC变换器[J].中国电机工程学报，2018, 38(1): 232–241.

[4] SEONG H W, KIM H S, PARK K B, et al. High step-up DC-DC converters using zero-voltage switching Boost integration technique and light-load frequency modulation control[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1383–1400.

[5] 吴琨，钱挺.一种带三绕组耦合电感的级联型高增益功率变换器[J].电工技术学报，2017, 32(20): 124–132.

[6] CHAN C Y. Investigation of voltage-mode controller for cascade boost converter[J]. IET Power Electronics, 2014, 7(8): 2060–2068.

[7] 雷浩东，郝瑞祥，游小杰，等.基于开关电容的软开关高电压增益DC-DC变换器[J].电工技术学报，2018, 33(12): 2821–2830.

[8] 李楠，王萍，贝太周，等.新型高增益开关电容直流升压变换器[J].电力系统及其自动化学报，2017, 29(6): 83–89.

[9] 侯世英，陈剑飞，孙韬，等.基于开关电容网络的DC-DC变换器[J].电工技术学报，2014, 29(10): 90–97.

[10] LIU H, HU H, WU H, et al. Overview of high-step-up coupled- inductor Boost converters[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2016, 4(2): 689–704.

[11] 曹太强，刘威，郭筱瑛，等.双耦合电感二次型高升压增益DC-DC变换器[J].电工技术学报，2015, 30(8): 104–112.

[12] 杨杰，于东升，朱虹，等.双耦合电感零输入纹波高增益QBC-VMU集成变换器[J].中国电机工程学报，2016, 36(23): 6501–6510, 6617.

[13] 马骏杰，孔维文，郝慎才，等.斩控式交流变换器的Simulink仿真实验[J].实验技术与管理，2017, 34(8): 125–128.

[14] 李文娟，王超，冯杰，等.双闭环控制的三电平逆变电路Simulink仿真实验[J].实验技术与管理，2016, 33(10): 110– 114, 134.

[15] 王博，邓明，王猛，等.基于Simulink的三相全控整流器仿真研究[J].实验技术与管理，2016, 33(1): 61–66.

[16] 陈龙，卢旺.基于滑模变结构控制的Buck型DC/DC变换器实验研究[J].实验技术与管理，2017, 34(11): 65–70.

Simulation analysis of a zero ripple high gain DC/DC converter

WANG Panpan, DUAN Sen, TONG Zhigang, YU Dongsheng, XU Yunzhi, HAN Li

(School of Electrical and Power Engineering, China University of Mining and Technology, Xuzhou 221116, China)

In order to solve the problems of insufficient boost capability and large input current ripple of traditional Boost circuit, a novel DC/DC converter based on coupled inductance is proposed. The zero input current ripple is achieved by combining coupling inductance and capacitance in the front stage of the converter, and voltage gain of the converter is expanded by using coupled inductance voltage doubling unit in the back stage of the converter. A clamping circuit with diode and capacitor is introduced to suppress the voltage spike caused by leakage inductance, thus forming a new converter topology. Based on the circuit theory, the working principle and working characteristics of the converter are analyzed, and by taking the DC boost stage in the photovoltaic power generation system as the application background, experimental verification and analysis are carried out on the Simulink simulation platform. The results show that the converter has the characteristics of the high voltage gain, zero input ripple and low voltage stress.

DC/DC converter; coupled inductor; simulation experiment

G642.0；TM46

A

1002-4956(2019)12-0107-06

10.16791/j.cnki.sjg.2019.12.025

2019-05-25

2019-06-26

国家自然科学基金项目（61703404）；江苏高校品牌专业建设工程资助项目（PPZY2015B132）；江苏省高等教育教改研究课题（2017JSJG127）；中国矿业大学教学研究项目（2018YB41）

王攀攀（1982—），男，浙江东阳，博士，讲师，主要从事新能源发电技术、工业自动化和电气设备故障诊断的教学与科研工作。